Динамическая модель анализа рисков при реализации строительных проектов на основе марковских случайных процессов

Одним из важнейших и актуальных направлений успешной реализации строительных проектов является учет и, как следствие, снижение организационно-технологических рисков в строительной сфере. Проявляются организационно-технологические риски на всех стадиях реализации строительных проектов, начиная от проектирования и заканчивая реализацией произведенной продукции строительства. Процесс реализации строительных проектов, комплексов работ или меро- приятий в современных условиях невозможно представить без анализа и оценки рисков при их выполнении, который проводится на основании разнообразных методов, моделей и подходов [1–3].

Учет рисков в строительной сфере основывается на трех базовых аспектах, которые лежат в основе успешного завершения строительных проектов [4]:

• – временной аспект, результатом выполнения которого является завершение строительных проектов в заданные сроки;

• – стоимостной аспект, который подразумевает то, что реальная стоимость реализации строительного проекта не будет превышать заранее определенной сметы;

• – качественный аспект, который предполагает, что качество строительного объекта будет не ниже допустимых пределов.

В контексте данных аспектов и учитывают потенциальные риски при реализации строительных проектов. Соответственно, в зависимости от направленности воздействия рисков зависит и возможный ущерб от наступления негативных ситуаций.

Основной проблемой для их учета является то, что риски возникают под влиянием случайных факторов в условиях высокой неопределенности [5, 6]. Поэтому подавляющее большинство методов учета рисков в строительстве основываются на вероятностных моделях. Учитывая то, что в последнее время уровень неопределенности практически во всех сферах хозяйственной деятельности значительно вырос, требуется разработка новых подходов к анализу рисков, которые бы максимально точно и быстро реагировали на возникающие угрозы.

Таким образом, направление научных исследований, связанное с разработкой новых и усовершенствованием имеющихся подходов к учету рисков в строительной сфере, является актуальным и практически востребованным в настоящее время.

Целью данной работы является разработка математической модели учета негативного влияния неблагоприятных факторов на реализацию строительных проектов в динамике их поступления в условиях высокой неопределенности. Математическая модель основана на теории марковских случайных процессов. Сначала приведем предпосылки ее использования для анализа рисков в сфере строительства.

Предпосылки использования теории случайных процессов при анализе рисков в строительстве

Как было сказано ранее, при проведении строительных работ свойственна ситуация, когда условия их проведения меняются быстро и непредсказуемо, развитие событий носят вероятностный характер и предсказать точно влияние внешних условий на результат реализации строительного проекта оказывается невозможно. Моделирование процесса реализации строительных работ с течением времени в таких ситуациях возможно только в вероятностном подходе и модель должна основываться на стохастических методах.

Для динамического моделирования процесса реализации строительных работ и проектов, в том числе с учетом возможного риска от воздействия негативных факторов, рационально использовать математические методы моделирования, основанные на теории марковских случайных процессов с непрерывным временем и дискретным состоянием [7–9].

Для применения данной модели необходимо обязательное требование, чтобы переходы между состояниями системы реализации строительных проектов, которые обозначим как S i и S j , осуществлялись под влиянием некоторого потока событий с интенсивностью λ ij , который связан со средним временем Т_i j нахождения системы в состоянии S_i перед переходом в состояние S j . При этом данный поток событий должен быть потоком Пуассона [7].

Согласно [10], пуассоновские и близкие к ним по структуре потоки событий часто встречаются в задачах реализации строительных и иных проектов, на которые оказывают воздействие как позитивное, так и негативное большое число случайных внешних факторов. Учитывая это, при моделировании процессов ведения строительных работ чаще всего идет наложение (суммирование) потоков событий, связанных с влиянием внешних факторов различной природы, или их случайное разрежение, поэтому чаще всего воздействующие случайные факторы, обуславливающие эти потоки, являются независимыми. Это дает основание с высокой точностью для математического моделирования применять теорию марковских случайных процессов с дискретным состоянием для динамического описания степени риска и ущерба в вероятностном подходе [11].

При построении математической модели сделаем еще одно допущение и будем считать, что интенсивности переходных потоков событий λ ij являются стационарными, то есть их параметры не зависят от времени. Если же возникнет необходимость рассматривать нестационарные потоки событий с интенсивностью, зависящей от времени λ _i j ( t ), то на необходимом для анализа временном интервале реализации строительного проекта от t 1 до t 2 можно использовать среднюю интенсивность переходных потоков λ ij , которая для этого временного интервала можно усреднить интегрированием:

t ₂

λ ij = ∫ t ⋅λ ij ( t ) dt .

t ₁

Таким образом, можно обоснованно сказать, что для построения динамической модели анализа рисков в вероятностном подходе при реализации строительных проектов и проведении комплексов работ рационально использовать теорию марковских случайных процессов с непрерывным временем и дискретным состоянием.

Математическая модель задачи

Рассмотрим некоторый строительный проект, комплекс работ или строительных мероприятий, который находится в стадии реализации. Если на данный проект не воздействуют факторы внешней среды или их воздействие незначительно и не может повлиять на изменение процесса реализации проекта в худшую сторону, то проект реализуется в соответствии с планом, вероятность его завершения в соответствии с проектной документацией считается достоверной, риски нулевые, и будем называть такой процесс реализации строительного проекта плановым.

В случайные моменты времени могут возникать некоторые обстоятельства, которые мешают нормальному процессу реализации строительного проекта и которые вызваны негативным влиянием внешней среды, риски в срыве плановой реализации проекта возрастают. Будем называть эти обстоятельства негативным влиянием или проявлением негативных факторов.

Для более точного моделирования рационально дифференцировать негативное влияние по степени его воздействия на реализацию строительного проекта.

Введем три категории негативных факторов по степени приносимого ими ущерба:

• – факторы, способные принести слабый ущерб плановой реализации проекта;

• – факторы, способные принести умеренный ущерб;

• – факторы, способные принести значительный ущерб плановой реализации строительного проекта.

Понятно, что такое разделение негативного влияния и рисков, с ним связанных, субъективно, но всегда методами экспертного оценивания [11] при реализации конкретных строительных проектов можно отнести негативные факторы к той или иной категории.

С другой стороны, при влиянии негативных факторов система организации строительства пытается их ликвидировать или нивелировать, минимизируя ущерб и пытаясь перейти к плановой реализации строительного проекта. Мероприятия ликвидации угроз зависит от характера и объема негативных внешних воздействий, оперативной ситуации и времени, отводимого на ликвидации угроз.

В качестве числовых характеристик, определяющих процесс поступления внешнего негативного воздействия и его ликвидации при реализации строительных проектов, определим временные параметры:

• T 0 – среднее время между проявлением негативных факторов за время плановой или иной реализации строительного проекта;

• T 1 – среднее время ликвидации фактора, способного принести слабый ущерб плановой реализации проекта;

• T 2 – среднее время ликвидации фактора, способного принести умеренный ущерб плановой реализации проекта;

• T ₃ – среднее время ликвидации фактора, способного принести значительный ущерб плановой реализации проекта.

Также стоит ввести следующие вероятностные параметры:

• р ₁ – вероятность того, что при негативном влиянии будет причинен слабый ущерб (или, по-

• другому, доля негативных факторов, способных причинить слабый ущерб плановой реализации проекта среди всего множества негативных факторов);

• р ₂ – вероятность того, что при негативном влиянии будет причинен умеренный ущерб;

• р ₃ – вероятность того, что при негативном влиянии будет причинен значительный ущерб.

Введем следующие состояния случайного процесса:

• S ₀ – реализация строительного проекта находится в плановом состоянии;

• S ₁ – на процесс реализации строительного проекта начали влиять негативные факторы, которые могут привести к слабому ущербу, проводятся мероприятия по их ликвидации;

• S 2 – на строительный проект начали влиять негативные факторы, которые могут привести к умеренному ущербу, проводятся мероприятия по их ликвидации;

• S 3 – на строительный проект начали влиять негативные факторы, которые могут привести к значительному ущербу, проводятся мероприятия по их ликвидации.

Переходы между состояниями случайного процесса, интенсивности переходных потоков, приводящих к смене состояний, а также особенности их получения, приведены в табл. 1.

Таблица 1

Переходы между состояниями случайного процесса и их характеристики

Table 1

Transitions between states of a random process and their characteristics

Переход между состояниями	Интенсивность переходного потока	Пояснения к переходу
S 0 – S 1	λ 01 = p 1/ T 0	При плановой реализации строительного проекта возникли негативные факторы, способные привести к слабому ущербу
S 0 – S 2	λ 02 = p 2/ T 0	При плановой реализации строительного проекта возникли негативные факторы, способные привести к умеренному ущербу
S 0 – S 3	λ 03 = p 3/ T 0	При плановой реализации строительного проекта возникли негативные факторы, способные привести к значительному ущербу
S 1 – S 0	λ 10 = 1/ T 1	Влияние факторов, способных привести к слабому ущербу, ликвидировано, процесс строительства вернулся к плановому режиму
S 1 – S 2	λ 12 = p 2/ T 0	При ликвидации негативных факторов, способных причинить слабый ущерб, произошло поступление новых негативных факторов, способных причинить умеренный ущерб, производится ликвидация негативных факторов. Если возможный ущерб при появлении новых негативных факторов ожидается слабый, то это не меняет состояния случайного процесса
S 1 – S 3	λ 13 = p 3/ T 0	При ликвидации негативных факторов, способных причинить слабый ущерб, произошло поступление новых негативных факторов, способных причинить значительный ущерб, производится ликвидация негативных факторов. Если возможный ущерб при влиянии новых негативных факторов ожидается слабый, то это не меняет состояния случайного процесса
S 2 – S 0	λ 20 = 1/ T 2	Влияние факторов, способных привести к умеренному ущербу, ликвидировано, процесс строительства вернулся к плановому режиму
S 2 – S 3	λ 23 = p 3/ T 0	При ликвидации негативных факторов, способных причинить умеренный ущерб, произошло поступление новых негативных факторов, способных причинить значительный ущерб, производится ликвидация негативных факторов. Если возможный ущерб при влиянии новых негативных факторов ожидается слабый или умеренный, то это не меняет состояния случайного процесса
S 3 – S 0	λ 30 = 1/ T 3	Влияние факторов, способных привести к значительному ущербу, ликвидировано, процесс строительства вернулся к плановому режиму

На основании данных из табл. 1 можно построить граф состояний случайного процесса, который изображен на рис. 1.

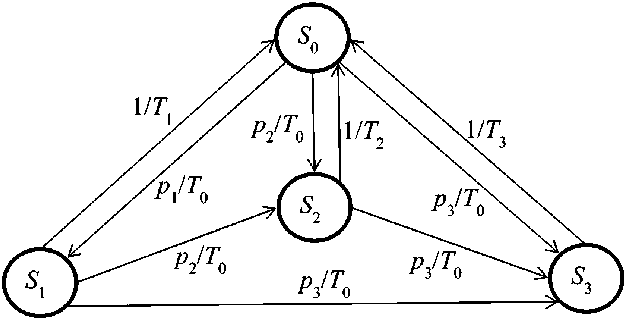
Рис. 1. Граф состояний случайного процесса Fig. 1. Graph of states of a random process

Для описания динамики ликвидации негативных факторов с разными последствиями их влияния по модели марковских случайных процессов необходимо вычислить временные зависимости вероятностей каждого состояния: P 0 ( t ), P 1 ( t ), P 2 ( t ), P 3 ( t ), которые имеют смысл вероятности того, что в произвольный момент времени t случайный процесс будет находиться в состоянии S ₀, S 1 , S 2 либо S 3 . Вероятность исходного состояния P 0 ( t ) будет равна вероятности того, что реализация строительного проекта находится в плановом состоянии.

В соответствии с графом состояний, который изображен на рис. 1, можно построить матрицу переходных интенсивностей переходных потоков λ ij , i = 0, 1, 2, 3; j = 0, 1, 2, 3, которая приведена в табл. 2.

Таблица 2

Матрица интенсивностей переходных потоков случайного процесса

Table 2

The matrix of intensities of transient flows of a random process

Состояния	S 0	S	S 2	S 3
S 0	0	p 1/ T 0	p / T 20	p / T 30
S	1/ T 1	0	p / T 20	p / T 30
S 2	1/ T 2	0	0	p / T 30
S 3	1/ T 3	0	0	0

Из рис. 1 и табл. 2 видно, что случайный процесс является эргодическим и на основании матрицы интенсивностей переходных потоков случайного процесса для нахождения вероятностей состояний составляем систему дифференциальных уравнений Колмогорова [8] вида:

Г dP o (t )_ P - ( t ) P . ( t ) P , ( t ) P o ( t ).

—11 ;

dt T    T 2     T 3     T o

dPi( t) — pl- Po( t) - P( t) ■ ( 1 + P11PX ) ; dt T0 ^ T-       To (1) ^ dP>( t) dt — p^ ■( Po( t) + P-( t))-P,( t) ■ T0 f -1- + P3-1; 1T. To J dP^1 — P?- ■( Po( t) + P( t) + P.( t))-^. dt    T0                         T3

Система уравнений (1) содержит линейно зависимые уравнения, и для получения частного невырожденного решения можно одно из уравнений системы заменить на необходимое условие нормировки вида:

Po( t) + P( t) + P,( t) + Рз( t) = 1, сделаем это с последним уравнением. В итоге получим систему дифференциальных уравнений вида:

' dP 0 ( t )	P 1 ( t )    P 2 ( t )    P 3 ( t )    P 0 ( t ) =                 1                   1                   '                  ;
dt	T 1      T 2	T 2      T 0
dP i ( t )	= P 1 P )( t ) - P 1 ( t ) •	' 1 + P 2 +	Pl ) ;
J dt	T 0	1 T 1      T 0
dP , ( t ) dt	=^2- • ( P )( t ) + P 1 ( t ) ) - P , ( t ) • T 0		[ 1 + P 3 1 T 2   T 0
[ P >( t ) + P 1 ( t ) + P , ( t ) + Р з ( t ) = 1.

Для нахождения решения системы дифференциальных уравнений (2) в численном виде используем начальные условия:

P o (0) = 1; P (0) = 0; P , (0) = 0; P 3 (0) = 0;                                                          (3)

которые имеют смысл того, что в начальный момент времени система находилась в состоянии S 0 .

Выражения (2) и (3) представляют собой систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами [12, 13], которую можно решать разными методами, например, данную систему рационально решить методом собственных значений и собственных векторов [14] либо использовать численные методы с привлечением вычислительной техники.

Анализ результатов

В результате численного решения с использованием математического пакета прикладных программ Mathcad удалось найти численное решение задач (2) и (3), которое в виде графиков представлено на рис. 2. В качестве параметров задачи возьмем типичные их значения, свойственные большинству строительных проектов: T 0 = 6 сут, T 1 = 2 сут, T 2 = 3 сут, T 3 = 4 сут, р 1 = 0,4, р 2 = 0,3, р 3 = 0,3.

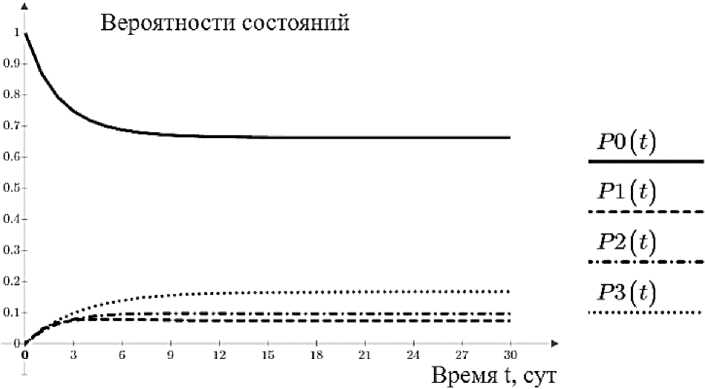
Рис. 2. Динамика изменения вероятностей состояний за 30 суток Fig. 2. Dynamics of changes in the probabilities of states for 30 days

Здесь наиболее интересной является вероятность состояния S ₀, характеризующего нахождение строительного проекта в плановом состоянии. Из рис. 2 видно, что вероятность этого состояния убывает от начального единичного значения до значений порядка 0,7, что позволит оценивать безрисковую долю времени выполнения строительного проекта. Вероятности состояний

P 1 ( t ), P 2 ( t ) и P 3 ( t ) напротив, позволяют с течением времени оценивать риски причинения слабого, умеренного и значительного ущерба соответственно.

Также интересно рассмотреть вопрос, как вероятностные параметры р 1 , р 2 и р 3 влияют на вероятности состояний. Управлять этими параметрами можно путем анализа рисковых ситуаций, профилактическими действиями и иными мероприятиями, снижающими возможный для реализации строительных проектов ущерб.

Зависимость влияния вероятностных параметров р ₁, р ₂ и р ₃ на временную зависимость вероятности P 0 ( t ) представлена на рис. 3. На графиках отражены три кривые, соответствующие доминированию негативных факторов с разным уровнем ущерба. Как и ожидалось, наибольшее влияние оказывает фактор, интенсивность которого наибольшая.

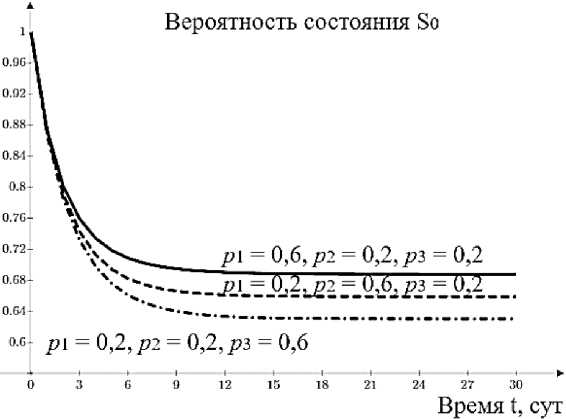
Рис. 3. Влияние вероятностных параметров на вероятность состояния S 0 Fig. 3. Influence of probabilistic parameters on the probability of the state S 0

Также рассмотрим влияние временных параметров на вероятность состояния S ₀, которое приведено на рис. 4. В качестве основного фактора возьмем среднее время нахождения строительного проекта в плановом состоянии Т ₀.

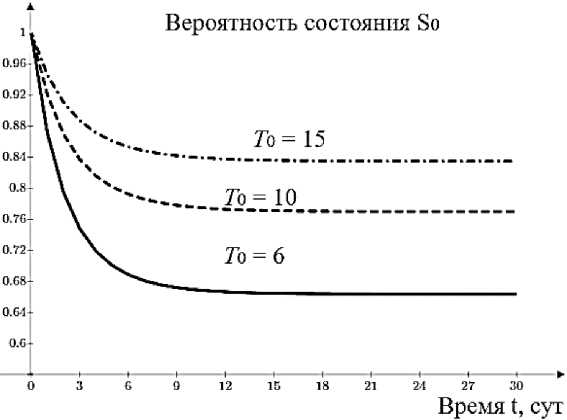
Рис. 4. Влияние временных параметров на вероятность состояния S 0

Fig. 4. Influence of time parameters on the probability of the state S 0

Графики показывают, что увеличение среднего времени нахождения строительного проекта в плановом состоянии значительно влияет на вероятность безрискового состояния, повышая его.

Анализ рисков при длительной реализации строительного проекта

Из рис. 1–4 видно, что с течением достаточно небольшого времени вероятности состояний приближаются к постоянным значениям и уже слабо зависят от времени. Это обусловлено тем, что все состояния случайного процесса являются транзитивными и сам случайный процесс является эргодическим [7]. Следовательно, с течением времени случайный процесс должен переходить в стационарный режим, когда вероятности состояний не будут завесить от времени. Такие вероятности P_i принято называть финальными [7, 9]:

p i — lim p ( t ), г — 0,1, 2,3. t ^x

Как показывают графики, изображенные на рис. 1, случайный процесс переходит в режим, близкий к стационарному уже через 10 суток после начала реализации строительного проекта.

Рассмотрим стационарный режим подробнее. Для нахождения финальных вероятностей необходимо решать систему алгебраических уравнений [7]:

—

PPPP

— + — + — + — = 0;

T 0

T 1

T 2

T 3

p 1

P ₀

T ₀

—

7⁺ к T 1

p 2^±^3 !• p — 0;

T 0    ^{J 1}

p 2

P ₀

T ₀

+ P 2 p

T 0 ¹

—

(„к

± + p ³ • p = 0;

к T 2    T 0 ^{J 2}

p ) + p 1 + p 2 + p j — 1.

Можно исключить из системы (4) переменную Р 3 , сократив число уравнений, а также учесть, что р ₃ = 1 – р ₁ – р ₂, что позволит сократить число параметров. В итоге вместо (4) можно записать:

( 1      1 к

— + — • P _o +

T    T I ⁰

к Т 0 T 3 )

к Т 3

—

—]• p +

T 1 ^{J 1}

¥ к Т 3

—

p —    •

T ₂ J ²    T 3 ’

p 1 _P

T ₀

—

7⁺ к T

1- p ¹ ]• p — 0;

T 0 )

p 2 _P

T ₀

+ p^ p

T 0 ¹

—

T + к T2

1 — p1 — p 2

T 0

• p₂ — 0.

Систему алгебраических уравнений (5) несложно решить аналитически, такое решение будет иметь вид (для сокращения записи вновь введен параметр р ₃):

P o =

TT + T — p ₁ T ₁)( T ₀ + p 3 T 2 )

P l —

( T 0 + T 1 )( T > + T 2 — p 2 T 2X T + p 3 T 3 ) ’

— P 1 T 0 T ( T 0 + p 3 T 2 )        ,

P 2 —

( T + T 1 )( T 0 + T 2 — P 1 T 2 )( T 0 + p 3 Т3У p ₂ T ₀ T ₂

( T 0 + T 2 — P 1 T 2 )( T 0 + P 3 T 3 )’

p 3 — 1 — p 0 — p 1 — p 2 .

Полученные аналитические зависимости (6) позволяют проводить анализ влияния параметров задачи на финальные вероятности. На рис. 5 приведена зависимость финальной вероятности Р 0 , которую можно интерпретировать как среднюю долю времени, которую проводит строительный проект в плановом состоянии S ₀ по истечении длительного времени.

Зависимости финальной вероятности Р0 от среднего времени ликвидации негативного воздействия разного типа показывают, что среднее время ликвидации угроз со слабым ущербом оказывает наименьшее влияние на вероятность нахождения строительного проекта в плановом состоянии при краткосрочном времени ликвидации этих угроз, а при длительном времени наименее опасными становятся негативные факторы с умеренным ущербом. Наибольшее воздействие оказывают факторы, приносящие значительный ущерб, хотя разница небольшая и зависит от вре- менных параметров. Эти зависимости позволят оптимально распределять ресурсы при проведении профилактики влияния негативных факторов на строительный процесс.

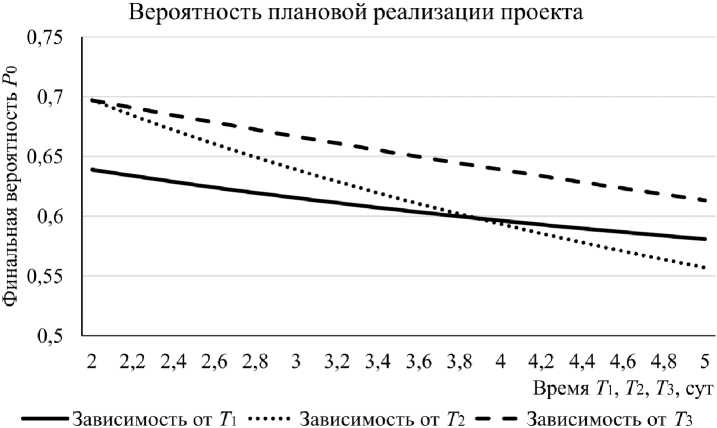
Рис. 5. Графики влияния временных параметров Т 1 , Т 2 и Т 3 на финальную вероятность состояния S 0

Fig. 5. Graphs of the influence of time parameters T 1 , T 2 and T 3 on the final probability of the state S 0

Заключение

Таким образом, была представлена динамическая модель, позволяющая оценивать вероятности причинения ущерба той или иной степени процессу выполнения строительных проектов, комплексов работ и мероприятий в зависимости от времени. Зная вероятности P ₁( t ), P ₂( t ) и P ₃( t ), характеризующие возможность влияния негативных факторов, которые могут нанести соответственно слабый, умеренный или значительный ущерб строительному проекту, а также определив через U 1 , U 2 и U 3 величину такого ущерба, можно, используя формулу для математического ожидания, определить средний ущерб U ( t ), который может быть причинен строительному проекту в произвольный момент времени его реализации t :

U ( t ) = U 1 ■ P 1 (t) + U 2 ■ P 2 (t) + U 3 ■ P 3 ( t). (7)

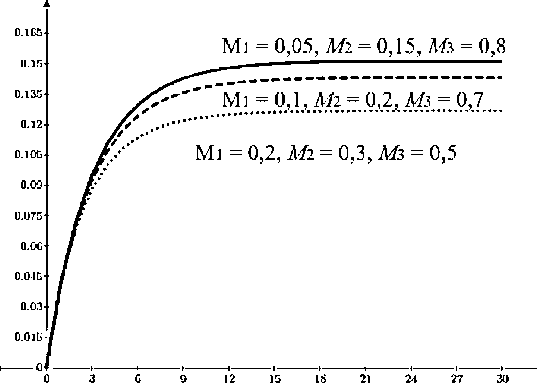
Рассчитанный по формуле (7) средний ущерб принято называть риском строительного проекта [15]. На рис. 6 приведены временные зависимости риска строительных проектов для различных величин ожидаемого ущерба, которые указаны на графиках в виде весовых множителей.

Время t, cyr

Рис. 6. Величина риска для разного распределения ущерба

Fig. 6. The magnitude of the risk for different distribution of damage

Приведенная динамическая модель оценки риска при реализации строительных проектов может служить основой для построения системы оптимального управления ходом выполнения строительных работ и принятия решений по организации строительных мероприятий.