Динамика и точность микромеханического гироскопа с учетом смещения инерционной массы

Создание высокоточных микромеханических гироскопов (ММГ) для решения задач навигации и управления движением подвижных объектов является актуальной задачей приборостроения [1]. Одним из достоинств ММГ является малая масса и габариты, а также небольшая стоимость (относительно гироскопов, построенных на других физических принципах, таких как, например, волоконно-оптические и лазерные гироскопы). При этом одним из главных недостатков ММГ является нестабильность метрологических характеристик и низкая точность измерений угловой скорости объекта. Принцип функционирования вибрационных гироскопов основан на свойстве маятника Фуко сохранять неизменной в инерциальном пространстве плоскость малых колебаний маятника [2].

Основы теории гироскопов класса обобщенного маятника Фуко и, в частности, ММГ изложены в работах [2-8], где рассмотрены различные схемы построения таких гироскопов, изучено влияние инструментальных погрешностей изготовления, условий функционирования, а также геометрической и физической нелинейностей на точность прибора.

Исследования в этой области нашли отражение и в работах зарубежных авторов [9; 10]. Так в публикации [10] проводится оценка уходов гироскопа на основе построенной математической модели, описывающей медленное изменение амплитуд и фаз колебаний чувствительных элементов (ЧЭ) и элементов орбиты колебаний. В работе [9] обсуждаются проблемы, возникающие при конструировании ММГ, и анализируются уравнения колебаний ММГ. Также в статье [9] составляются уравнения движения для ММГ с угловым и линейным осцилляторным типом движения ЧЭ (R-R и L-L типа, соответственно).

В целях повышения точности ММГ в данной работе исследуются колебания ЧЭ ММГ R-R типа с учетом явлений разнодобротности и разно-частотности, а также эффектов, возникающих из-за смещения центра масс ЧЭ относительно центра карданова подвеса. Смещение центра масс появляется ввиду несовершенства технологии изготовления и сборки прибора. Поставлена задача повышения точности ММГ путем построения новой математической модели колебаний ЧЭ ММГ с учетом указанных выше инструментальных погрешностей и аналитической компенсации ухода гироскопа в линейном приближении.

• 1    Уравнения колебаний задачи

Рассматривается конструкция микромеханического вибрационного гироскопа R-R типа с промежуточной рамкой [3]. Кинематическая схема гироскопа представляет собой двухстепенной карданов подвес ЧЭ. Конструкционная схема прибора приведена на рис. 1.

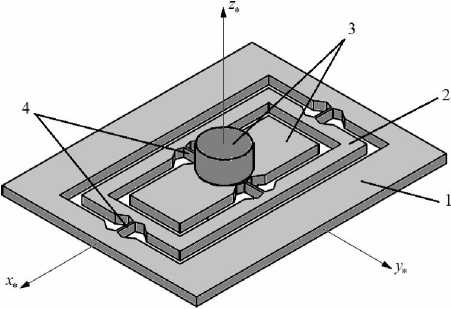
Рис. 1. Конструкционная схема прибора

Для описания положения чувствительного элемента 3 введем системы координат (рис. 2): Ox * y * z * — связанную с основанием гироскопа 1 (корпусом прибора), причем ось Oz * совпадает с осью чувствительности гироскопа; Ox 1 y 1 z_x — связанную с промежуточной рамкой подвеса 2 ; Oxyz — связанную с внутренней рамкой, к которой закрепляется дополнительный элемент для увеличения момента инерции подвижной части системы. Начало координат - точка O находится в геометрическом центре упругого подвеса .

Учитывая, что гироскоп имеет одну ось чувствительности к угловому движению основания, будем рассматривать влияние угловой скорости основания Ω на малые колебания рамок карданова подвеса по двум обобщенным координатам - по углам а и в закручивания торсионов 4 .

В силу рассматриваемой кинематической схемы выражение для проекций ® ₂ x , ® ₂ y , ® ₂ z вектора ю ₂ угловой скорости внутренней рамки на оси Oxyz имеют вид:

го2x = a cos в -^ cos а sin в, rn2y = в + Q sin а, (1) го2z = а sin в + ^ cos a cos в.

Будем полагать, что конструкция системы обеспечивает бесконечную жесткость на изгиб. В расчетном случае сбалансированного ЧЭ центр масс — точка C внутренней рамки и жестко закрепленной на ней дополнительной инерционной массы находится в центре подвеса и совпадает с точкой O .

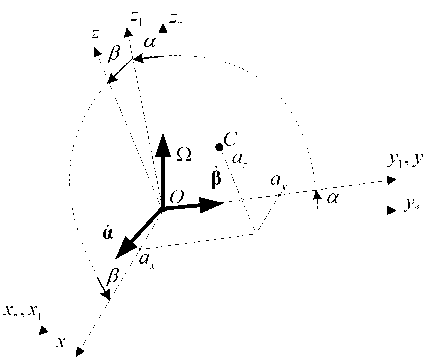
Рис. 2. Системы координат

В осях Ox 1 y 1 z_x зададим тензор инерции промежуточной рамки J 1 — diag ( J 1 _x , J 1 y , J 1 _z ), где J 1 _x , J 1 y , J 1 _z — соответствующие осевые моменты инерции промежуточной рамки. Для расчетного случая сбалансированной внутренней пластины карданова подвеса с дополнительной инерционной массой введем тензор инерции J ₂ — diag ( J _{2 x} , J ₂ y , J _{2 z} ), где J 2 _x , J ₂ y , J ₂ z — осевые моменты инерции в соответствующих осях Oxyz . Смещение инерционной массы зададим тремя постоянными компонентами a_x , a y , a_z вектора, соединяющего геометрический центр упругого под -веса и центр масс ЧЭ, в системе координат Oxyz .

Составим уравнения динамики ЧЭ ММГ с помощью теоремы об изменении момента количества механической системы [0]:

d K 2                 d K i

—— +[Ш2, K2 ]— L2,       + [^1, K1 ] — L tt где L1 — главный момент всех внешних сил, действующих на систему «промежуточная рамка — ЧЭ», а L2 — главный момент всех внешних сил, действующих на ЧЭ. К внешним силам в данной работе относятся моменты упругости, возникающие при скручивании торсионов, и силы, характеризующие потери на внутреннее трение в материале и описывае-мые моделью Кельвина — Фойгта.

Момент количества движения для системы «внутренней рамки и инерционной массы» в проекциях на оси Oxyz имеет вид:

K 2 =

^J 2 + m 3

2 . 2

a y ⁺ a z - aa

- a x a y

2 ,     2

a„ + a

- a_xa_z

- a a yz

- a_xa_z

- a_ya_z

2 ,     2

a, + a

• ^ 2 ,

а момент количества движения для системы «промежуточная рамка — ЧЭ» в проекциях на оси Ox ₁ y ₁ z ₁:

^ cos Р 0

sin Р ^

K, — J. • ю. +

0      1

_v- sin Р 0

cos в

K ₂.

Здесь для нахождения момента инерции системы «внутренняя рамка — инерционная масса» была применена теорема Гюйгенса — Штейнера, а Ю 1 — ( a Q sin a Q cos a ) ^T — вектор угловой скорости промежуточной рамки в проекциях на оси Ox ₁ y ₁ z ₁.

Подставляя выражения (1), (3) и (4) в уравнения динамики (2) и выписывая их в проекциях на оси торсионов, получим нелинейные уравнения движения ЧЭ ММГ. При переходе от нелинейных уравнений к уравнениям малых колебаний отбросим слагаемые, характеризующие нелинейность, связанную с геометрией движения. Влияние этой нелинейности на динамику прибора исследовано в работах [5; 6].

В случае постоянной угловой скорости прибора уравнения малых колебаний имеют вид:

- a

'                 Qe      ji где введены следующие обозначения:

J x 2 ⁺ J y 2    J z 2

x 2 ⁺ ° y 2    ° z 2

m 3 a x ²

m ₃ a_y ²

m 3 a z ²

J y 2

Здесь j ₁, j ₂ — безразмерные массово-геометрические параметры; e x , ^ _y , ^ _z — приведенные безразмерные моменты инерции ЧЭ; rn _a , ® _в — собственные частоты колебаний по углам a , Р соответственно; Q _a , Q _p — добротность колебательного контура по углам a и Р соответственно; d _a , d _e — коэффициенты демпфирования; c _a , c _p — коэффициенты жесткости торсионов; m ₃ — дополнительная масса. Для уменьшения демпфирования колебательного контура применяют конструкционные материалы с низким коэффициентом внутренних потерь при колебаниях, а также обеспечивают требуемую степень вакуумирования корпуса прибора.

Анализ экспериментальных данных по измерению малых колебаний системы позволяет оценить параметры системы, в частности характерные частоты и демпфирование системы. В силу достаточно высокой добротности колебательного контура имеется возможность проводить оценку углового движения основания гироскопа в режиме свободных (неуправляемых) колебаний.

При получении уравнений колебаний (5) угловая скорость прибора полагалась малой по сравнению с собственной частотой, т. е. |Q| = « _a .

Учитывая, что правая часть уравнений (5) представляет собой малые возмущения, т. е. a + « a a = O ( s ) , то с указанной точностью можно записать a = — « a a + O ( s ) . Таким образом, в правой части (5) можно избавиться от вторых производных углов a и Р . В случае равенства собственных частот колебаний и отсутствия смещения инерционной массы уравнения (5) совпадают с известными результатами [5].

Характеристики точности ММГ существенно зависят от соотношения собственных частот « и « _Р . Расчетные массово-геометрические параметры системы выбираются из условия обеспечения внутреннего резонанса в системе, т. е. при равных собственных частотах. Однако, как было указано в работах [3; 4; 8; 9], неизвестные и непредсказуемые отклонения элементов конструкции от проектных значений, приводят к разночастот-ности, поэтому введем малую разночастотность ст/2 в системе:

«a = «0, «Р = «0 (1 + ^2).

Здесь « — характерное значение собственной частоты колебаний, принимаемое равной собственной частоте « . При принятых обозначениях получим безразмерные уравнения колебаний чувствительного элемен- та с точностью до слагаемых первого порядка малости в виде: a + «2a = ji^p -    + «0 (у + ^z )a - ^^p),

Q a

^Р + « 0 ^Р =- j 2 O ^{a -} —^{- с}« 0 ^{Р +} '/^ ( ^{( y} x ^{+ X} z ) ^Р - V ^X x ^X y ^a ) . Q P              Ji

Система уравнений динамики (7) является одночастотной системой дифференциальных уравнений с малыми возмущениями в правой части, называемой регулярно возмущенной системой [12], для исследования которой будем использовать асимптотические методы.

Решение нелинейных уравнений (7) будем искать методом осреднения Крылова — Боголюбова [12] для медленно меняющихся переменных «амплитуда — фаза» A , B , ф 1 и ф ₂ :

a = A sin («01 + ф1), a = A«0 cos («01 + ф1), P = B sin («01 + ф2), p = B«0cos («01 + ф2).

Проводя процедуру осреднения [12] по явно входящему времени t , получаем осредненную систему уравнений:

A' = - -A - + j¹— B cos ф

2 Q a    ² ® 0        ¹

— ф2 ) +

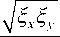
B sin ( ф - ф 2 ) ,

B' = ——— j ²^ A cos ф - ф ₂ ) 2 Q , 2 м ^W

yr y— A ^sin ( Ф 1 ^- Ф 2 ) , 2 j ₁

Аф\ = -

£fe + -z)    jj^               \-y

---- ----A - — ^B sin ( ф 1 - ^ 2 ) ⁺ ,  ^B cos ^ф 1 - ф 2 ) , 2         2 to ₀                    2

Г ° ^x + ^z ) j2

^B Ф 2 =--------—

-

22 j 1

B - J j^L a sin ( ф 1 - ф 2 ) + V x y ²¹ a cos ( ф 1 - ф 2 ) . ² ® 0                    ^{2 j} 1

Штрихом в (9) обозначено дифференцирование по безразмерному времени т = o ₀ 1 . Полученная модель в линейном приближении описывает свободные колебания ЧЭ гироскопа на подвижном основании.

• 2    Решение уравнений колебаний в частном случае

Рассмотрим случай расположения центра масс инерционной массы на одной из осей торсионов, т. е. ax = 0 или ay = 0. Указанный случай пред- ставляет интерес из-за возможности получения аналитического решения системы дифференциальных уравнений (9). Полученные решения могут быть использованы для построения методик идентификации параметров, а также оценки ухода гироскопа и его учета с помощью методики алгоритмической компенсации. При таком допущении система уравнений при неподвижном основании ф = 0) примет вид:

A ' = - —A , 2 Qa B ' = — B , 2 Q e

А ф 1 =- 2 ( ^ y + ^ z ) A , 1 .       .            ч              (10) B Ф 2, =- ° - — ( ^ x + ^ z ) B . 2 I      j 1            )

Решение этой системы можно записать в виде:

f    1    ) A (т) = A (0) exp - ——т 1, V   Qa  ) f    1    ) B(т) = B(0)exp -^т , V 2 Qe  ) ф1 (T ) = - 2 (^y + ^z )T + ф1 (0), f      .            .             (11) ф2 (T ) = | ° - j2- (^x + ^z )|T + ф2 (0), 2 V     j1           ) где A0 = A (0), B0 = B (0), ф10 = ф1 (0), ф20 = ф2 (0) — начальные условия.

Возвращаясь к исходным переменным, решение примет вид:

a( t) = A (0) exp

в (t) = B (0) exp

—

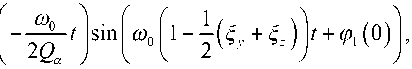
-^ 0- 1 sin ² Q e J

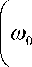
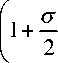
j                        .^

— ~ Ux + ^z ) It + ф2 (°)

^{2 j} 1            J J

Таким образом, смещение инерционной массы из центра подвеса приводит к расщеплению собственных частот системы. Полученное аналитическое решение может быть использовано при обработке стендовых испытаний прибора.

• 3    Сравнение результатов моделирования с экспериментом

Для оценки адекватности построенной модели сравним результаты моделирования с экспериментальными данными. В качестве измерительной информации, получаемой из системы наблюдения, имеем медленно меняющиеся переменные Ван-дер-Поля p ₁, q ₁, p ₂, q ₂ [5], которые связаны с углами a и в соотношениями:

a = p 1 sin ( ® ₀ 1 ) + q 1 cos ( ® ₀ 1 ) , в = p ₂ sin ( ® ₀ 1 ) + q ₂ cos ( ® ₀ 1 ) . (13)

Получение информации осуществляется с помощью электростатических датчиков. Учитывая, что решения получены в переменных «амплитуда — фаза», то для их сравнения необходимо пересчитать амплитуды по экспериментальным данным по формулам:

a = V P 1 ² + q 2 ,     в = V p 2 + q 2 ,               (14)

а для обратного перехода справедливы соотношения:

p 1 = A cos ф 1 , q 1 = A sin ф 1 , p ₂ = B cos ф ₂, q ₂ = B sin ф ₂. (15)

Экспериментальные данные были получены для прибора со следующими числовыми значениями параметров математической модели:

Q„ = 3856,   Q_r = 3938,   j = 1.35 - 10 ^{— 3},   j, = 1.46 - 10 ^{— 3},

a             7    в-р             7   j 1                    7    j 2                    7

(U, + U z ) = 0.2 - 10 ^{— 5},

- — j^2- (U + U )^ = 3-10—5,

( 2 2 j/ "x "z J)         , а начальные условия были приняты равными значениям переменных Вандер-Поля из измерения в начальный момент времени:

p10 = 13.467-10—3, q10 = 20.429-10—3, A0 = 24.468-10—3, ф10 = 0.988, p20 = 0.787-10—3, q20 = 1.172-10—3, B0 = 1.412-10—3, ф20 = 0.978.

Сравним поведение зависимостей амплитуд A и B от безразмерного времени т , которые приведены на рис. 3. Как видно по рис. 3 демпфирование колебаний в эксперименте соответствует решению (11). А учет явления разнодобротности ( Q _a ^ Q _p ) обеспечивает близость зависимостей каждой из амплитуд к соответствующим экспериментальным данным. На рис. 3–5 цифрой «1» обозначены зависимости, полученные по результатам моделирования, а цифрой «2» — экспериментальные данные.

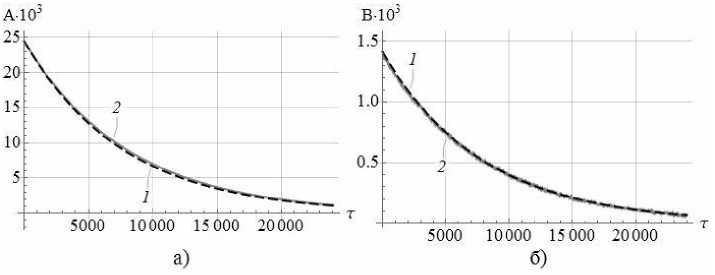
Рис. 3. Зависимости амплитуд A и B от безразмерного времени τ

При проверке решения для медленно изменяющихся фаз (11) возникают трудности с вычислением значений обратных тригонометрических функций для зашумленных экспериментальных данных. Поэтому проверку поведения для фаз будем проводить сравнением зависимостей переменных Ван-дер-Поля от времени. При этом для получения аналитических выражений для p ₁, q ₁, p ₂, q ₂, соответствующих решению (11), в формулы перехода (15) будет подставлено решение для переменных «амплитуда — фаза». В результате графики зависимостей медленно меняющихся переменных Ван-дер-Поля представлены на рис. 4.

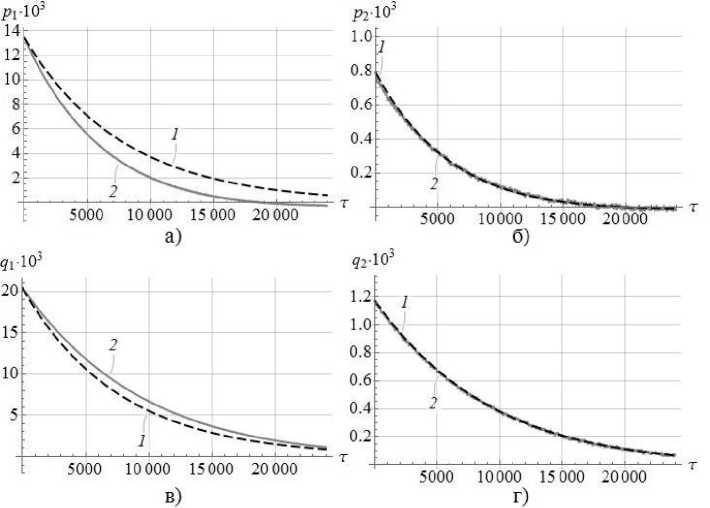
Рис. 4. Зависимости переменных Ван-дер-Поля p ₁, q ₁, p ₂, q ₂ от безразмерного времени τ

По графикам рис. 4 видно, что для переменных p ₂, q ₂ имеем достаточно точное совпадение результатов моделирования и экспериментальных данных. Для переменных p ₁, q ₁ наблюдается небольшое расхождение в числовых значениях при качественном совпадении зависимостей. Эти расхождения могут быть объяснены нелинейными эффектами, в частности, упомянутой выше геометрической нелинейностью [5; 6]. Учет нелинейных эффектов при построении математических моделей ММГ, увеличивает точность приборов и, как следствие, инерциальных навигационных систем на их основе [1; 2; 6].

Для оценки ухода гироскопа, связанного с нелинейными или побочными эффектами, введем вспомогательный функционал I , характеризующий угол прецессии орбиты колебаний ЧЭ [5; 10]:

I =  2\ir (qiq2 + Pip2) = 2jlAB cos ф - ф)

j2 (q2 + Pi2)-j (q2 + p2)        j2A2 -jB2’ для которого справедливо соотношение:

6 = 1 arctan I,(17)

T где 6 = -KJ^(t, ) dT1 — угол, пропорциональный интегралу от угловой 0

скорости, а K = ^ j 1 j ₂ /2 — масштабный коэффициент.

I =

При подстановке решения (11) в выражение (16) получим:

4KA0B exp f Qa- + Qi --— т { 2 ) f cos 1 <7 -[ f j2 (^x + ^z )         Y ^У ^z < J\                   )_ т , Y 2 + Лф0 J j2 A02 exP (-Q1T ) - hi BO exP (-Q1T )

Здесь А ф ₀ = ф ₂₀ - ф ₁₀ — разность фаз в начальный момент времени.

На рис. 5 представлена зависимость расчетного ( 1 ) и экспериментального ( 2 ) значения функционала I от безразмерного времени т . Анализ значений функционала I , рассчитанного по экспериментальным данным, показывает на существенную зависимость функционала от амплитуды колебаний и шумов измерений. При уменьшении амплитуды колебаний отношение полезного сигнала к шуму измерений уменьшается и, соответственно, увеличиваются погрешности в определении ухода гироскопа.

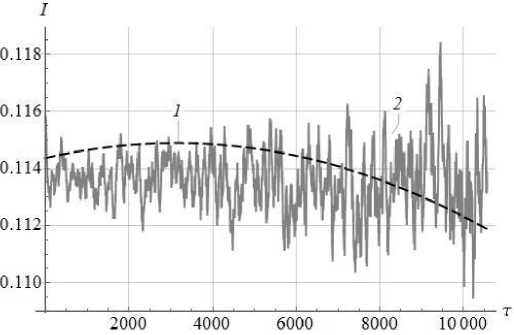
Рис. 5. Зависимость функционала I от безразмерного времени

Точность построенной модели оценим по относительным погрешностям амплитуд колебаний 5 A и 5 В , которые будем рассчитывать по формулам:

5 A = |( A e - A m М A m | '100%, 5 В = |( B e - В т )/ В т | • 100%. (19)

Здесь нижнему индексу « e » соответствуют значения амплитуд, рассчитанные по экспериментальным данным; а индексу « т » — значения амплитуд, полученные по решению (11). Графики зависимостей соответствующих относительных погрешностей от безразмерного времени представлены на рис. 6.

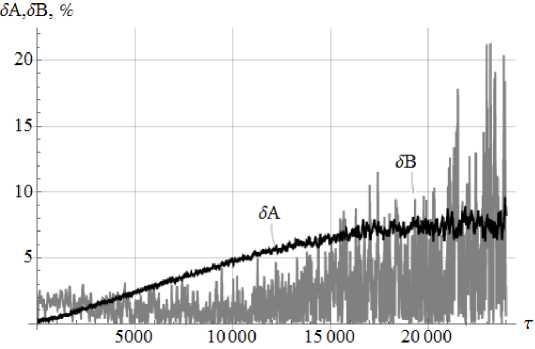
Рис. 6. Зависимости относительных погрешностей для амплитуд

5 A и 5 В колебаний

Из графиков рис. 6 видно, что относительная погрешность для амплитуды 5 A не превышает 8,75%, а для амплитуды 5 В — 21,3%.

Полученные значения характеризуют адекватность построенной математической модели малых колебаний ЧЭ. Уточнение параметров математической модели с помощью методики идентификации параметров позволит увеличить точность ММГ путем алгоритмической компенсации систематического ухода гироскопа, вызванного разнодобротностью, разно-частотностью и смещением инерционной массы относительно геометрического центра упругого подвеса.

Заключение

Построенная новая математическая модель ММГ R-R типа описывает динамику гироскопа на подвижном основании с учетом инструментальных погрешностей изготовления – малой неравножесткости и разнодоб-ротности упругого подвеса, а также малого смещения центра масс чувствительного элемента относительно центра упругого подвеса. Проведенный сравнительный анализ результатов математического моделирования с экспериментальными данными подтверждает адекватность разработанной модели колебаний ЧЭ ММГ.

Результаты работы могут быть использованы для повышения точности прибора с помощью алгоритма аналитической компенсации систематических погрешностей гироскопа.