Динамика одноименно заряженных проводящих шаров вблизи инверсии силы электростатического отталкивания

В работах [1–5] были найдены критические расстояния L между одноименно заряженными сферами, при которых сила отталкивания становится равной нулю, а при дальнейшем сближении сфер меняется на силу притяжения. Было показано, что критическое расстояние зависит от отношения радиусов сфер R2 /R1 и отношения зарядов на сферах q1 /q2 . Примеры зависимости относительной силы электростатического взаимодействия двух шаров от расстояния между центрами сфер для трех отношений радиусов приведены на рисунке. В качестве единицы расстояния принят радиус меньшего (первого) шара.

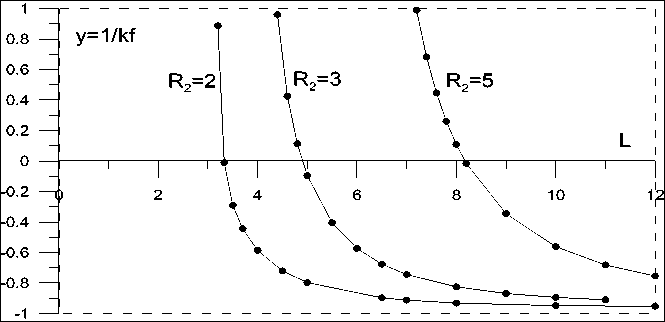
Отношение силы электростатического взаимодействия к силе отталкивания соответствующих точечных зарядов одноименно заряженных сфер в зависимости от расстояния между центрами сфер

По вертикали на рисунке указано от- талкивания, вычисленной по закону Кулона ношение электростатической силы к силе от- для соответствующих точечных зарядов ------------------------------- F = q 1 • q 2 / 4 ^п ^ о L .

Как видно, при больших расстояниях между сферами отношение сил стремится к -1. Значениям расстояний больше критического соответствует ослабленная сила отталкивания, а значениям расстояний меньше критического соответствует сила притяжения. Приведенные зависимости соответствуют равным зарядам на проводящих сферах q 1 = q 2 . Влияние отношения зарядов на критическое расстояние было исследовано в [5]; показано, что при q 1 <  q 2 (номер 1 относится к шару с меньшим радиусом) критическое расстояние увеличивается, а при q 1 >  q 2 уменьшается.

Результаты [1–5] были получены путем решения методом сеток трех задач Дирихле для потенциала поля. Две вспомогательные задачи позволяли определить по методу Робена [6] потенциалы на сферах при задании зарядов на них, а в третьей задаче определялись характеристики электрического поля.

Возникает естественный вопрос – как скажется обнаруженная инверсия силы на динамике заряженных проводящих тел? Для ответа на этот вопрос требуется критическое рассмотрение соответствующих задач динамики [7] – движение в поле центральных сил, задача Кеплера, упругое столкновение тел, рассеяние тел, колебания.

В данной статье лишь упоминаются ожидаемые эффекты в задачах динамики. Более подробно рассмотрена задача о колебаниях, так как ожидаемая асимметрия колебаний может быть использована для экспериментального определения критических расстояний в зависимости от отношения радиусов шаров, отношения зарядов, а также от формы проводящих тел. Для более полного ответа на вопросы об эффектах динамики заряженных проводников потребуются детальные вычислительные и лабораторные эксперименты.

В задачах о движении заряженных проводников следует ожидать необычные эффекты лишь в тех случаях, когда расстояние между телами приближается к критическому L = L * . Так, например, в задаче облета малой частицы вокруг большой при прицельных расстояниях p >  L „ ситуация будет близка к классической задаче о движении тел при отталкивании [7].

Однако при p < p* < L* ситуация резко изменится, так как частица войдет в зону, в которой сила отталкивания сменится на силу притяжения. В этом случае последует соединение частиц. Критическое прицельное расстояние p будет зависеть от отношения радиусов, отношения зарядов и от начального импульса. Определение этих зависимостей планируется в дальнейшем.

Сделаем критическое замечание об используемом допущении – мгновенной перестройке силы электростатического взаимодействия. Время перестройки наведенных зарядов в проводнике вероятно мало, но все равно оно конечно. Поэтому желательно обнаружить ситуации, в которых можно будет оценить скорость перестройки индуцированных зарядов, и в дальнейшем учесть соответствующие эффекты.

Экспериментальное подтверждение полученных в [1–5] значений критических расстояний между сферами может быть подтверждено путем обнаружения асимметричности колебаний на расстояниях, близких к критическому L „ .

В данной статье проанализированы результаты решения задачи о колебаниях двух тел в случае, когда сила, возвращающая тела к равновесному расстоянию, различна для положительных и отрицательных отклонений. В качестве колебательной системы может быть выбрана ситуация математического маятника или колебание тел, связанных упругой силой. С математической точки зрения эти задачи одинаковы.

Рассмотрим подробнее математическую постановку задачи о малых колебаниях заряженных проводников. Предполагается, что два шара связаны между собой упругой силой и силой кулоновского электростатического взаимодействия. Для упрощения задачи полагаем, что координаты второго тела зафиксированы и поэтому требуется определить зависимость от времени лишь координаты одного (первого) тела.

Уравнения свободных колебаний первого тела имеют вид mx + k (x)x = 0. (1)

Полагаем, что равновесному значению координаты x = 0 соответствует критическое расстояние между сферами. Для зависимости коэффициента к(x) вблизи L можно использовать простые аппроксимации к (x ) = к1 = к0 (1 - ^1) при x > 0,

к ( x ) = к 2 = к ₀ ( 1 + ^ ) при x <  0 . (2)

В этих формулах коэффициенты µ ₁, µ ₂ выражены в долях величины k ₀ , которая соответствует возвращающей силе в случае не заряженных тел. Вычислительные эксперименты [1–5] обнаружили различные значения коэффициентов µ ₁, µ ₂ и, следовательно, k ₁, k ₂ . Так, например, при отношении радиусов R 2 / R 1 = 2 отношение k 2 / k 1 около 1,2.

Используя закон сохранения энергии для амплитуд колебаний x ₁, x ₂ , находим простую формулу для отношения амплитуд колебаний:

D = X i / x 2 = kkjk= = 1 + ^ 2 . (3) V1 - p

Отсюда видно, что при значениях µ ₁, µ ₂ близких к единице отношение амплитуд колебаний велико и поэтому легко может быть обнаружено. Так, например, при p. 1 = p ₂ = 1/5 отношение амплитуд составляет около 1,225, а при p 1 = p ₂ = 3/5 это отношение равно 2.

Вывод

Показано, что значения критических расстояний между заряженными телами, обращающих в ноль силу отталкивания одноименно заряженных проводящих шаров, могут быть сравнительно просто подтверждены в лабораторных исследованиях путем обнаружения асимметрии свободных колебаний. Кроме того, в этих экспериментах может быть выяснено и влияние геометрии заряженных проводников (например, эллипсов).

Высказана гипотеза о конечной скорости перестройки индуцированных зарядов.