Динамика стержневой большой орбитальной космической системы цепочечной структуры

Особенностью поведения космических систем рассматриваемого вида является хаотический характер вращательных движений стержней в механической системе с большим числом степеней свободы. На параметры этого движения определяющее влияние оказывают массы точек, длины стержней, нелинейность гравитационного поля и дифференциальных уравнений движения системы и, естественно, начальные условия при численном моделировании [1, 2, 3].

1.    Описание механической системыВывод уравнений движения

Рассматривается движение механической системы, состоящей из M (i = 1,2,..., n +1)  материальных тел, соеди ненных последовательно n невесомыми стержнями с длинами lj (j = 1, 2,..., n). Тела принимаются за материальные точки мас-

сами m_; ( i = 1, 2,..., n + 1 ) . Точки движутся в плоскости в центральном гравитационном поле. Длины стержней достаточно велики и такие, что позволяют называть систему S , образованную точками m , БОКС – большой орбитальной космической системой цепочечной структуры.

Движение механической системы S происходит под действием сил притяжения G к Земле:

• - Mm. -

• Gi = -Y —3^Ri, (i = 1,2,..., n +1), (1) Ri

где у - гравитационная постоянная, M -масса Земли, m – масса i -го тела, R – радиус-вектор i -го тела. Сила G направлена от i -го тела к центру Земли.

Для построения математической модели движения БОКС рассматриваемой структуры введем неподвижную связанную с Землей систему координат OXY и зададим обобщенные координаты системы. Положение первого тела будем определять радиус- вектором R (t) и углом его поворота v(t) относительно оси OX . Положения остальных тел зададим углами рj (j = 1,..., n) отклонения стержней l относительно оси OX (рис. 1).

M 1 :

M :

X j = R ( t ) cos v ( t ) , y_x = R ( t ) sin v ( t ) , x₂ = X j + l j cos ^ ( t ) , . y 2 = y 1 + 1 i sin ^ 1 ( t ) ,

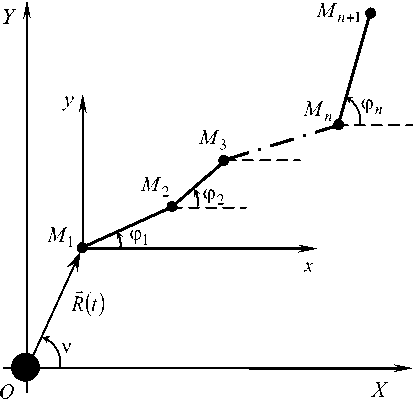
Рис. 1. Большая орбитальная космическая система цепочечной структуры

M n + 1 :

^u i , ⁽ i = ¹

'x n + 1 = x n ⁺ l n cos ^ n ^{( t} ) , . У п + 1 = У п ⁺ l n sin P n ^{( t} ) -

Из равенств (4) определяются скорости

,...,

тел системы и значение

кинетической энергии T системы S :

^u i = X\ ⁺ yi , n + 1             1 n + 1        ,                .

T = Z T . = 7 Z m i ( X 2 + y 2 ) , ■     (5)

i = 1          ² i = 1

( i = 1

,...,

Обобщенные силы Q определяются проекциями гравитационных сил G_i :

G x_i

Mm x

^—Y R

—

Mm x ■ Y / ,

Система S имеет в рассматриваемом случае n + 2 степени свободы, соответственно вектор-строка обобщенных координат q , описывающая положение механической системы, имеет n + 2 координаты q_k :

q = ^{{ R ( t} ) ^{v ( t}\ P 1 ^{( t} \ —, Pn ^{( t )}} •      (2)

G y_i

( i = 1

Mm y

—Y—

—

W22

Xi + yi

Mm y

■ Y / .

I / 22

W Xi + y i-

,..., n , n +1 f      z^v

Q k = Z G x i    + G

‘=¹ [

^d q k

yi

dr ] , ^d q k J

,

,

Дифференциальные уравнения движения БОКС как голономной механической системы могут быть представлены в виде уравнений Лагранжа II рода:

( k = 1,

...

, n + 2 ) .

d (dr ^ — - dt rqk J

.T = Qk,  (k = 1, dqk

n + 2 ) , (3)

где T ( t , q_k , q_k ) - кинетическая энергия механической системы, q – обобщенные координаты, Q – обобщенные силы.

Запишем координаты тел механической системы в абсолютной системе координат XOY :

2. Исследование 5-массовой БОКС в транспортирующей системе координат

Исследование поведения системы проводилось на модели, состоящей из пяти тел. Определяющими параметрами системы S являются массы тел, длины стержней и начальные условия. Орбитальное движение системы M , M ,..., M задается движением первой точки, предполагая, что в начальный момент она находится на расстоянии R ₃ + H от гравитационного центра и имеет начальную скорость, соответствующую круговой скорости для этого расстояния

^U 0

у M

\ R 3 + H

где R ₃ – радиус Земли, H – начальная высота точки M над поверхностью Земли.

Начальное состояние системы полностью определяется размером и положением дуги полуокружности, на которой расположены точки M , M ,..., M в начальный момент времени, система S движется мгновенно-поступательно.

Ниже приводится анализ движения БОКС из пяти точек, соединенных последовательно, в транспортирующей системе координат M xy [1, 2, 3] (рис. 1), при этом массы всех тел одинаковы и равны m , длины всех стержней одинаковы и равны l (при этом 4 1 <<  H ).

Система в начальном положении S ₀ находится в четвертой четверти транспортирующей системы координат (ТСК), первая и пятая точки – на оси M y (рис. 2).

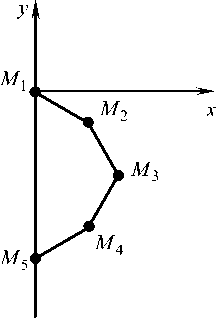
Рис. 2 . Начальное положение БОКС в ТСК

На первом этапе движения системы t e [t0, tj ] к моменту tx (рис. 3) происходит "выпрямление" – увеличение радиуса кривизны дуги, проходящей через точки M , M , M . Радиус кривизны дуги M M M увеличивается незначительно. Точка M незначительно смещается с оси M y в четвертую четверть ТСК. При этом угловая скорость первого стержня щ < 0, а угловые скорости других стержней щ > щ > щ > 0. Расстояние между точками M и M возрастает с 3000 м до 4000 м.

y

M 1 x

Рис. 3. Положение системы в момент времени t ₁

На втором этапе t e[t_{ , t ₂ ] при сохранении знаков угловых скоростей стержней на первом этапе к моменту t (рис. 4) второй, третий и четвертый стержни практически располагаются вдоль прямой M M . Стержень M M проходит нижнее "вертикальное" направление, точка M оказывается в третьей четверти ТСК. Кривизна дуги M M M меняет знак по отношению к кривизне этой дуги на первом этапе. Таким образом, при t e [ t j, t ₂ ] существует момент, когда точки M , M , M располагаются на одной прямой. Расстояние между точками M и M увеличивается до 4700 м.

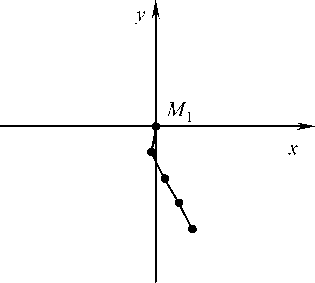
Рис. 4. Положение системы в момент времени t

На следующем этапе к моменту t меняется знак угловой скорости первого стержня MM^, соотношение щ > щ > щ сохраня- ется. Таким образом, все угловые скорости щ > 0 (i = 1,2,3,4). Система S остается в четвертой четверти ТСК, образуя фигуру выпуклостью "назад", пройдя состояние, близкое к симметричному по отношению к отрезку M M в начальном положении S , при условии, что этот отрезок составляет с осью минус M y угол порядка 700 . Расстояние между точками M и M уменьшается до 3500 м.

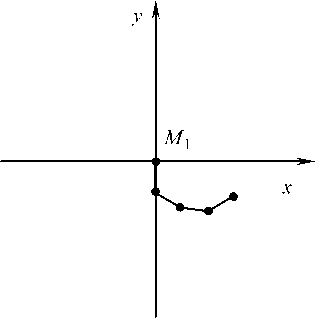
Рис. 5. Положение системы в момент времени t

На промежутке t e [ t ₃, t ₄ ] вращение четвертого стержня замедляется, щ &  0 . Соотношение между угловыми скоростями становится следующим:

щ >  щ >  щ >  ^ ₄ >  0.       (8)

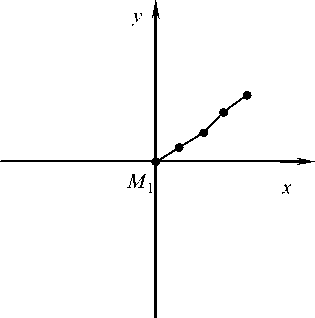
Рис. 6. Положение системы в момент времени t

Далее, при t e [ t ₄, t₅ ] условие (8) для угловых скоростей стержней системы S сохраняется. Все точки последовательно переходят из первой четверти во вторую, образуя симметричную относительно средней точки M фигуру с кривизнами k , k , k одного знака. Эта фигура, как и в начальном положении, снова обращена выпуклостью "вперед", в направлении вращения S вокруг опорной точки M .

Соотношение (8) между угловыми скоростями меняется на противоположное:

щ >  щ >  щ >  щ ,        (9)

причем с увеличением щ происходит уменьшение щ до отрицательных значений в моменты t и t (рис. 8 и 9).

Система точек S переходит из четвертого квадранта ТСК в первый и к моменту t все точки системы, как и на втором этапе, располагаются практически на одной прямой, образующей с осью M^x угол ® 40 °. Расстояние M M близко к максимальному: M M ₅ &  4 1 . Отклонения точек от прямой M M таковы, что дуги M M M и M M M , а также M M M имеют соответственно малые кривизны k , k , k чередующихся знаков, причем     |k ₂1« | k ₃1,

I ^k i| < k 2I.

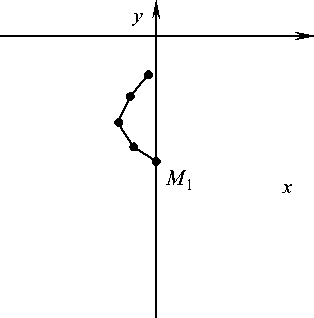
Рис. 7. Положение системы в момент времени t

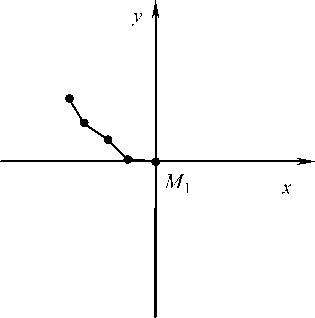
Рис. 8. Положение системы в момент времени t

На промежутке t е [t8, t9 ] и далее непрекра-щающееся изменение угловых скоростей к моменту t приводит к условию щ > щ > щ > щ. При этом на некоторых промежутках т = [t', t"]^[t9, tx0] в отличие от условия (8) щ < 0 .

Минимальное расстояние между точками M\M₅ х 2 1 , достигнутое при трапециевидной форме S , увеличивается, ю₄ растет. Отрезки l , l , l практически "выпрямляются" вдоль прямой M ₁ M ₄ . К моменту t система S приходит в третью четверть выпуклостью "вперед" вследствие малых значений

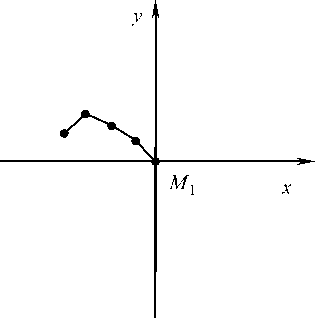
Рис. 9. Положение системы в момент времени t

Эти изменения угловых скоростей приводят к тому, что на момент времени t система S , оставаясь во второй четверти, образует трапециевидную фигуру, обращенную "выпуклостью" (меньшим основанием) "назад" (рис. 10).

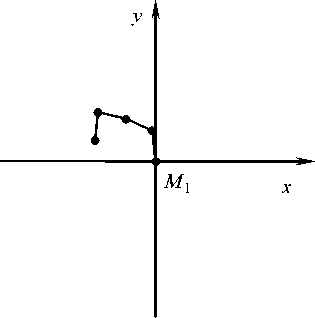
Рис. 10. Положение системы в момент времени t а 4.

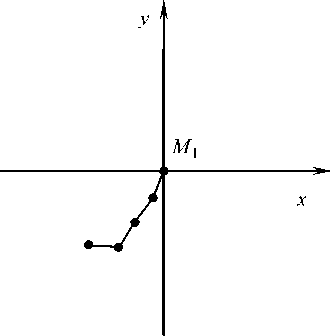
Рис. 11. Положение системы в момент времени t

Переход системы точек S из третьей четверти ТСК в четвертую происходит практически при равных щ >  0 с малым изменением относительного углового положения отрезков на предыдущем этапе t е [ t ₉, t j₀ ] .

Далее продолжается хаотическое движение точек системы с сохранением известных интегралов энергии и площадей для рассматриваемых условий орбитального движения.

Заключение

Математическая модель БОКС цепочечной структуры, описанная в данной работе, может быть использована для дальнейшего анализа больших космических систем.

Исследование движения 5-массовой системы проводилось численно с применением пакета Mathematica в предположении равных длин стержней, равных масс точек, мгновенно-поступательного начального состояния системы в плоском центральном гравитационном поле. Приведено описание последовательных состояний системы в транспортирующей системе координат на промежутке одного оборота системы вокруг гравитационного центра.

Создана визуализация движения 5-массовой системы.