Discovering the maximum clique in social networks using artificial bee colony optimization method

Published Online October 2019 in MECS DOI: 10.5815/ijitcs.2019.10.01

A network is an intra-link set or system of institutions and the corresponding communications among them which is aimed at sharing a capability or ability between two or more systems within a certain time and location range. However, in an ideal condition, a given network should not have time and location limitations.

The social network can be considered as an instance of such networks which include communications and human interactions. In other words, social networks are social structures which people and humanitarian organizations have built among themselves; hence, using it, they can interact with each other about predetermined subjects and issues. For example, the simplest social networks are family, relatives, tribe, friends, and colleagues. There is another type of social networks where people’s relations are established through a computer in the online form. To put it simply, this kind of social bases can be defined in the following way: an online community where its users are allowed to share information, pictures, videos, software, etc.; they are allowed to establish communications with other people and discover addresses for maintaining communications with new individuals [1]. Moreover, many social networks have numerous services and features such as email, photo sharing, music, audio and video for creating interactions among their users. In other words, in this type of bases, communicative elements such as email, message leaderboard, instant texting, and chat via audio, video and written media might be combined and brought together.

A graph data structure is mainly used for displaying and modeling social networks. Graph nodes play the roles of members and the edges play the roles of communications among the given individuals which may be one-way or two-way. The graph of real networks grows and develops fast in terms of the entrance of new individuals into the network environment and the establishment of new communications. Hence, it can be highlighted that real social networks are highly dynamic environments.

Since all users in a social network do not necessarily communicate with each other, the graph corresponding to the users may not be a complete graph. A clique is a complete subgraph of the main graph where all of its nodes communicate with all the other nodes [1]. In practice, a clique is a subset of social network users who follow a common goal or might have common interests and characteristics [2]. Finding such circles and cliques is of high significance in social networks because they can be useful in issues like enhancing advertisement and business effectiveness, discovering unofficial organizations and even discovering criminal and terrorist groups [3]. In his investigation, Krebs, 2002 focused on identifying criminal gangs and terrorist groups in the US using the available data about September 11, 2001 attacks on world trade towers, he extracted a subgraph including 37 nodes (people) about the perpetrators of the attack. Later, it was proved that all of them had roles in this terrorist attack [4].

In this paper, we investigated the issue of finding the maximal clique in a social network. Considering the NP-hard nature of the problem, we proposed a meta-heuristic method based on ABC optimization method for solving this problem. The proposed method was simulated in Matlab and the obtained results were compared with those of other methods. The proposed heuristic clique finder finds a large clique in the graph, which is often the maximum.

This paper is organized into 5 sections: in section 2, definitions, key concepts and common terminology are discussed and the related work is briefly reviewed. Section 3 introduces and describes the proposed method. Section 4 reports the results of simulating the computational and benchmark results. Finally, section 5 draws the conclusion of the study.

• II.    Related Work and Definition of Common Terminology

Couched in simple terms, each structure consisting of individuals which are established based on social relations can be referred to as a social network. Each social network encompasses a set of humans and their corresponding social relationship. Hence, it can be discussed that each social network consists of two elements: the entities that participate in communication and communication among these participating entities. In social science, the participating entities in communication are known as the actors and the respective communication among these entities is referred to as a relation. Social networks are divided into online and offline networks. Friends’ networks, colleagues’ networks and classmates’ networks in a working or education environment may be considered as instances of offline networks. On the other hand, social networks such as Facebook, Tweeter, and Google+ are examples of online social networks [5].

• A.    Clique Definition

In fact, proposing a comprehensive and precise definition for a clique in social networks is difficult and challenging because different definitions can be presented for different applications. A clique can be defined as is a complete subgraph of a larger graph. Assuming a distance function between two vertices, cliques can be defined as sets of vertices which are located within short distances from one another. This definition is mainly used in data clustering.

The clique is a structural and topological feature of the graphs. Clique detecting algorithms have been presented for weighted and unweighted, directed and undirected, and the graphs obtained from the combination of them. From the viewpoint of overlap, cliques can be divided into two types: cliques which overlap with each other, and cliques whit no overlapping. Graphs involved with social networks are mainly the ones which overlap with each other. In other words, a vertex can be included inside several cliques. The graphs generated by models and the Facebook graph are examples of consisting overlapping cliques.

For providing an abstract concept of the clique, we first consider a simple undirected graph G=(V, E) where V={1,..., n} is a set of nodes ; E e V*V is a set of edges and ||V||=n and ||E||=m . Graph G is known as a complete graph if for each v, u ∈ V(u ≠ v) , the edge (u, v) exists in E . The clique C is a subset of V provided that the extracted subgraph G[C] from it is complete. A clique is called maximal if it is not included within a larger clique and it is known as the maximum if there is no other clique in the network larger than it. The size of the largest clique in graph G , referred to as the clique number, is displayed by the symbol ω (G) [4].

• B.    Review of the Related Work

  The first survey papers on the maximum clique problem were reported in 1994 and 1997. Wu and Hao, 2015 made a comprehensive study and published an updated survey on this issue. This survey includes different mathematical definitions of the problem, explanation of exact algorithms and heuristic approaches [6].

Numerous studies have been conducted on the issue of finding the maximum clique and several methods have been developed and presented based on deterministic, heuristic and meta-heuristic algorithms for sorting out this issue. More evolutionary algorithms such as Genetic Algorithm (GA) and ACO have been used in this domain of study. The clique-ant algorithm is a well-known algorithm which generates a large clique by using consecutive smart greedy technology based on ant colony optimization and adding vertices to repetitive minor cliques [7].

In addition, another ACO-based method is a combination of Simulated Annealing (SA) in [8], and

Tabu search in [9]. Although the combined new algorithms have produced good results, they have high practical complexity. In this study, Particle Swarm Optimization (PSO) algorithm is innovatively applied for enhancing the performance of ACO algorithm for finding a large clique in a social network graph.

Soleimani-Pouri, Rezvanian, and Meybodi proposed a new method based on ACO algorithm in which, the process of updating pheromones is performed using PSO method in order to achieve better results. The authors simulated their proposed method on standard datasets and the results indicated a better performance than that of the standard ACO algorithm [10].

Carrabs, Cerulli and Dell’Olmo addressed a kind of classic clique problem where graph edges have labels. This problem was concerned with finding a large feasible clique in which the edge set includes, at most, b ∈ Z⁺ different labels. Moreover, in case many of feasible cliques are large and have an identical size, they tend to decrease the number of labels. The authors investigated time complexity and specific cases; then, for solving it, they proposed a mathematical programming method through two different equations [11].

Li, Wang, and Cui introduced a unique algorithm for precisely detecting communities with common interests in weighted and unweighted networks. Common vertex, bridge vertex, and the separated vertex were introduced as the largest cliques. Firstly, all large cliques are extracted by an algorithm based on a deep search. Next, the two large cliques with certain rules can be merged and changed into a greater graph. Moreover, the algorithm proposed by authors can successfully find common vertices and bridge vertices among the communities. The experimental results, as well as some data on the real networks, indicated that the performance of the proposed algorithm is satisfactory [12].

Newman and Girvan, 2004 proposed a divider algorithm which is called GN. It recursively eliminates edges with the highest intermediate degree from the edge and produces a hierarchical tree. Then, divider communities can be obtained by cutting the hierarchical tree at different points. This method leads to the correction of defects in the traditional algorithms. Nonetheless, this method has its own shortcomings such as high time complexity and the lack of a definition for community structure in the network [13].

By starting the initial network from n independent communities, Newman, 2004 proposed a fast greedy algorithm for maximizing index. Each community had one vertex. By optimizing the index, he developed a new algorithm for inferring community structure from the network. The index is executed at the time O(md log n) for a network with n vertices and m edges where d refers to the depth of the dendrogram. This algorithm is notably faster than the majority of the traditional algorithms [14]. For solving the maximum clique problem, Newman, 2006 presented an algorithm by using eigenvector [15].

Wang, Chen, and Lu introduced a highly fast algorithm merely based on local information for identifying the community [16]. Chen, Fu, and Shang developed a fast and efficient algorithm by recursively extracting a node which has the closest relations with the community for obtaining a local optimal clique [17]. Jursa, 2012 improved the Östergård search method and proposed a new algorithm for finding the maximum clique if scale-free graphs [18]. Pallam Derényi, Farkas, and Vicsek proposed an intrusion clique algorithm to detect the sharing of community structure. They contended that a community can be considered as a system which consists of a number of small networks which are fully connected to one concept [19].

Rossi, Gleich, Gebremedhin, and Patwary introduced the fast parallel maximum clique algorithm for large scattered graphs. It was aimed at exploiting the features of social and information networks. This method shows an approximate linear execution time on real social networks which range from 1000 to 100000000 nodes. In an experiment on a social network with 1.8 billion edges, the maximum clique was detected and identified at about 20 minutes. In this method, a branch and bound strategy with new aggressive pruning techniques were used [20].

Conte, DeVirgilio, Maccioni, Patrignani, and Torlone investigated a distributed method by appropriately examining pole nodes and detecting cliques in social networks. This method depends on the two-level decomposition process. They demonstrated that this process is able to detect all large cliques [21]. Lu, Yu, Wei, and Zhang; Mitzenmacher, Pachocki, Peng, Tsourakakis, and Xu proposed a complicated randomized algorithm for finding the maximum clique on large-scale graphs [22, 23].

Dharwadker, 2006 demonstrated that each graph with n vertices and the δ minimum vertex degree, at least, has one large clique in the size of [n ⁄ (n-δ)]; these conditions are the best possible form for n and δ . It can be maintained that he achieved new boundaries on well-known coded numbers in terms of maximum and minimum vertex degree related to coded graphs [24]. Belachew and Gillis, 2017 used a rank-1 matrix approximation method for finding the maximum clique in a graph [25]. Badica, Badica, Ivanović, and Logofatu used constraint logic programming approach for solving the maximum clique problem. [26].

The study of the literature reveals that most of the research in this issue are performed before 2015 and reported studies in recent years have been decreased. The investigation and comparison of several studies in the related literature indicate that artificial bee colony optimization has not been applied yet for finding the maximum clique in social networks. Hence, in this paper, for addressing this research gap, we developed a novel method based on ABC optimization.

• C.    Methods and Materials

  ACO was first developed and introduced by Dorigo, 1992 [27]. Indeed, it is a population-based search method which has been inspired by the ants’ behavior for finding food and carrying them to the nest through the shortest path. While navigating their routes in nature, real ants leave a substance called pheromone on the ground. It

functions as a guide for the other ants so that they use it for going along the same path to find food or to find the way back to the nest. This substance is evaporated in the vicinity of the air and its thickness and density decrease. Thus, in shorter routes, the pheromone is thicker and denser; as a result, the probability of using it by other ants increases; finally, the shortest path is obtained [28].

PSO was firstly introduced by Kennedy and Eberhart, 1995 [29]. It is a population-based search method which has been derived from the behavioral patterns of birds. Each particle of the population has a variable position and velocity based on which it moves in the search space. Each particle saves and memorizes the position of the best solution (Pbest) which it has obtained up to now. Then, it measures its next movement based on a combination of its own best solution and other particles’ best solution (Pglobal) [30].

• III.    The Proposed Method

We first clarify the mathematical model of the respective problem. Next, we describe the proposed ABC-based algorithm for solving the problem.

The mathematical programming model of the problem

If the problem graph is given as G=(V, E) and the graph , as the complement of graph G , is defined in the following way [5]:

E={(i,j) I i,jeV; i^j and (i,j)^ E}(1)

The integer mathematical programming model of the maximum clique problem can be defined through equations (2), (3), and (4).

Maximize ω(G) = ∑ ∈

Subject to:

_

Xi + Xj < 1; ^ (i, j) e E(3)

xi ∈ {0 ,1};     i∈ V(4)

Where the binary variable x i states that whether the i^th node is a member of the clique or not. Equation (2) is the objective function of the model which indicates the total number of the nodes which are members of the clique; hence, it is desirable to be maximized. Relation (3) is added to avoid repetition and guarantees that any two members of be considered as clique members only once. Equation (4) states that the variable x i can only take the value of 0 or 1.

• A.    The proposed ABC-based algorithm

  This algorithm, firstly introduced in 2005, is a

population-based smart search method. It was inspired by the colony behavior of the real honeybees. These colonies which have been widely scattered across vast areas around the hive are concerned with collecting nectar from flowers. The initial search is done randomly by the employed bees so as to find flower gardens with more food sources. Next, via their special dance just above the located flowering area, inform the watching onlooker bees about the amount, quality, and direction of the identified flowering area. In this way, more bees head for the identified flowers for gathering nectar. Then, they try to identify other areas and flowers. Finally, the flower garden with the most food source is identified.

In the proposed method, employees bees examine graph nodes and identify the nodes with the most communications with other nodes since such nodes have more probability(desirability) for presence in the largest clique; this investigation is carried out by measuring the number of “1” in the adjacency matrix for each row (each row denotes one node). Each food source is assumed to be a possible solution to the problem since it is a graph of the main problem graph which forms a spot in the parametric space. By moving towards the nodes with the highest communication degree and, next, by moving randomly towards the adjacent points, the onlooker bees go through a set of nodes and produce a solution to the problem. This solution is, indeed, a set of connected nodes which are considered to be a subgraph of the network. In case this subgraph is complete, it can be maintained that a clique of the network has been identified where its size is equal to the number of nodes traveled through by the bees in the flower garden. This search is done in a certain number of iterations. Finally, the clique with the greatest degree is announced as a solution to the problem.

• B.    Structure of the solution in the proposed method

In the proposed method, as discussed above, each onlooker bee goes through a set of nodes and, in this way, establishes a solution to the problem. This solution is displayed by an n-member vector where n denotes the number of vertices in the graph. Hence, in every search iteration, each onlooker bee, at most, investigates the same number of graph vertices. The value of each matrix element of this vector is an integer within the interval [0, n] which indicates vertex number through which the bee has traveled. In producing the initial population, these values are randomly produced. For example, Fig. 1 depicts a solution produced by a bee for an 8-node graph.

1 2 3 4 5 6 7 8

7

1

4

8

7

1

4

5

Fig.1. A sample solution for 8-node network

In the above-mentioned example, the bee goes through the following vertices: 7, 1, 4, 8, 7, 1, 4 and 5. Given the random production of these numbers, duplicate values are likely to be registered for them. In measuring the fitness of the solutions produced by the bees, duplicate values are replaced with 0.

• C.    Generating the initial population

The initial population of bees is randomly created by means of a certain number of bees which is referred to as PopNum. Throughout the execution of the algorithm, new onlooker bees (new solutions) are created. After they are sorted according to the fitness degree, as many bees as the PopNum are retained and the remainder of them are eliminated. In this way, population size is kept fixed.

• D .    Measuring fitness

As mentioned earlier in section 2.3, in the proposed method, each complete network subgraph is tantamount to a flower garden and the number of nodes in the subgraph indicates the total amount of nectar or the desirability of that flower garden. Thus, the value of fitness function depends on the clique size discovered by the bee which is measured by equation (2). The larger the discovered clique (complete subgraph with a higher number of vertices), the fitter the solution compared with the other solutions. The clique with the highest number of vertices is reported as the ultimate solution in the last iteration of the algorithm. For finding the maximum clique in the graph, the relations among the vertices are examined. These relations should be in such a way that all the vertices are connected to each other, i.e. the graph would be complete. The solutions produced by the onlooker bees are investigated and the ones with no duplicate or zero vertexes are retained, otherwise, they are eliminated. Then, the relations among them are investigated according to the adjacency matrix of the graph. If all the vertices in the current solution have relations with each other, it is regarded as a clique and its size is reported according to the number of available vertices in it. As a case in point, Fig. 2 illustrates a network with 8 vertices. It is assumed that there are two bees and the number of nodes traveled by them is given in Table 1. The discovered clique by these bees is given in Table 2.

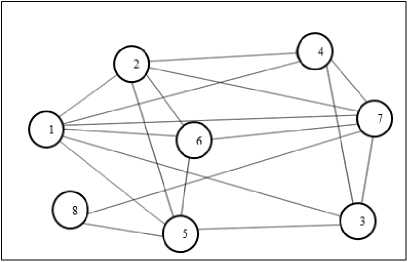
Fig.2. A network with 8 nodes

At this stage, the relations among the vertices are investigated. It is searched whether each of the vertices has relations with the other vertices or not. The unrelated nodes and the duplicate vertices are replaced with zero.

The fitness function investigates solutions based on the graph and, finally, reports the clique size. Hence, according to Table 1, the first bee investigates 8 vertices and eliminates duplicates vertices and the ones which do not have relations with the other vertices. As a result, the first bee will be able to find a 4-vertex clique which includes the nodes {7, 3, 1, 4}. However, the second bee finds a 3-vertex solution including the nodes {3, 5, 1}. Hence, it can be argued that the solution of the first bee is fitter than the solution of the second bee. The synopsis of these measurements is given in Table 2.

Table 1. Generated solutions by two bees in 8-node network

Bee #       Node numbers traversed by bees

Bee 1        4      1      1      3      8      7      5      4

Bee 2        1      7      1      5      4      5      3      6

Table 2. The calculated objective function for sample solutions of Table 1

Bee #	Traversed node numbers by bees		Clique Size
Bee 1	4   1     0     3     0     7     0	0	4
Bee 2	1   0     0     5     0     0     3	0	3

• E.    Local search in the proposed method

In the proposed method, bees randomly search for cliques with a predetermined amount of mutation. In each iteration, by having a new position of vertices, they investigate the graph randomly. As a result of examining the vertices, the first duplicate vertex is eliminated and is replaced with a new vertex of the graph which has not been traveled yet by the bee. Then, the search for finding the clique is restarted. An instance of such a search is given in Table 3.

Table 3. Replacing new node during local search

Status	Node numbers traversed by Bees
Before Mutation	4      1      1      3      8      7	5	4
After Mutation	1     7     6     3     8     7	5	3

• IV.    Simulation and Computational Results

  For evaluating the efficiency of the proposed method, it was simulated and compared with the examples adopted from [24] where a deterministic method is proposed for solving the problem and the global optimal solutions are calculated. The specifications of these instances are given in Table 4. Simulation of the proposed method was conducted on a PC with an Intel Core i5-4200 CPU in Matlab R2015b. The parameters and the results obtained from executing the proposed method are given in Table 5.

Table 4. The specifications of the simulated examples

Example Number	Graph Name	# of Nodes	# of Arcs
1	The Tetrahedron	4	6
2	The Octahedron	6	12
3	The Complement of the Bondy-Murty Graph G1	7	9
4	The Turán Graph T3, 8	8	21
5	The Complement of the Cube	8	16
6	The Complement of the Petersen Graph	10	30
7	The Complement of the Bondy-Murty graph G2	11	27
8	The Complement of the Grötzsch Graph	11	35
9	The Complement of the Herschel Graph	11	37
10	The Icosahedron	12	30
11	The Complement of the Bondy-Murty graph G3	14	70
12	The Complement of the Bondy-Murty graph G4	16	105
13	The Ramsey Graph R(4,4)	17	68
14	The Complement of the Folkman Graph	20	150
15	The Complement of the Thomassen Graph	34	509
16	The Complement of the Berge Graph	60	1620
17	The Complement of the Witzel Graph	450	83198

As given in Table 5, the results obtained from the deterministic and the proposed method were only slightly different with respect to example 17. In other cases, the proposed method was able to achieve an optimal solution. Considering the random nature of meta-heuristic methods where there is no guarantee for achieving an optimal solution, we used large-scale examples adopted from real social networks for evaluating the proposed method and comparing it with other meta-heuristic methods. In the proposed method, ACO and the combination of the Ant Colony Optimization (ACO) and Particle Swarm Optimization (PSO), referred to as PS-ACO, were also simulated. The computational results and their comparisons are given in the next section.

The output results produced by the proposed method for the examples 15, 16 and 17 are depicted in figures 3,

5 and 7. In each figure, red spots indicate member nodes of the identified largest clique. According to the figures, these nodes are distributed on the whole network and are not centralized. So it can be concluded that that the clique members on a large network like Facebook, may belong to different countries and regions. In other words, the physical metric distance among clique members is not important and each of the members may belong to a different city or country. The convergence of the objective function until achieving the final solution in the respective examples are shown in figures 4, 6 and 8. The convergence diagrams show the behavior, speed, and slope of the proposed method reaching the final solution. In these figures, the horizontal axis denotes the iteration number and the vertical axis indicates the value of the fitness function.

Table 5. Simulation parameters and computational results of the proposed method

Example Number	Pop Num	# of Iterations	Largest clique size obtained by		Execution Time (Sec.)
			The proposed method	Deterministic method*
1	4	5	4	4	0.018239
2	4	6	3	3	0.018057
3	4	6	3	3	0.017829
4	4	8	3	3	0.018933
5	4	8	4	4	0.002602
6	4	8	4	4	0.018867
7	4	8	4	4	0.017966
8	6	8	5	5	0.019061
9	8	10	6	6	0.003884
10	10	15	3	3	0.023288
11	10	15	7	7	0.032326
12	10	15	9	9	0.023376
13	10	15	3	3	0.021933
14	10	15	10	10	0.040575
15	12	20	14	14	0.062574
16	16	20	20	20	0.127405
17	50	60	28	30	12.249485

* Proposed by Dharwadker (2006)

Fig.3. The Complement of the Thomassen Graph

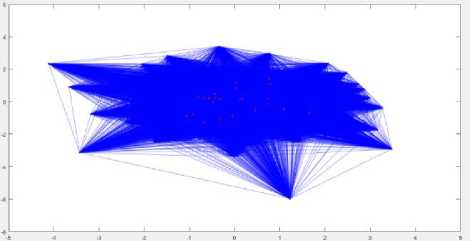
Fig.7. The complement of Witzel graph and a detected clique of size 27

Fig.4. The convergence diagram of the complement of the Thomassen graph

As the figures 3, 5 and 7 show, the clique members do not make a symmetric structure and they are spread on the whole graph. Cliques of a graph may also overlap, which means a specific node is a member of two or more cliques at the same time.

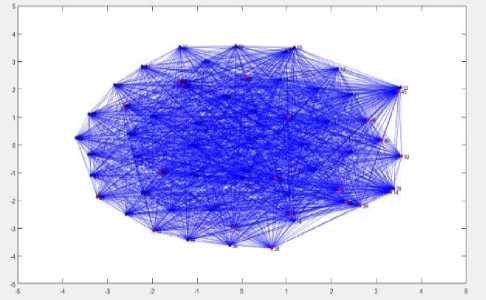
Fig.5. The complement of the Berge Graph and the detected clique of size 20

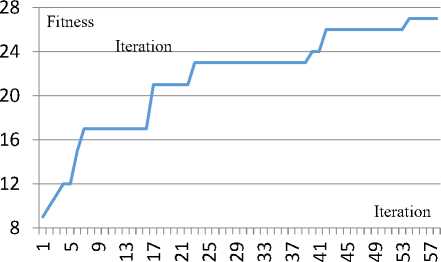
Fig.8. The convergence diagram of the complement of the Witzel graph

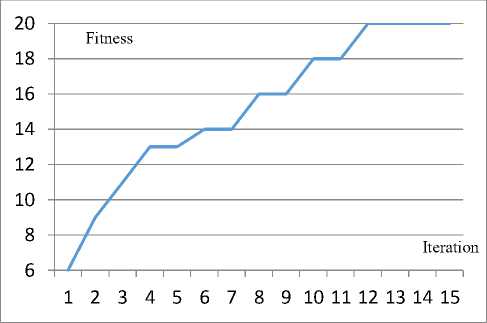
Fig.6. The convergence diagram of the complement of the Berge graph

For examining the stability of the proposed method, we executed the example 17, the largest available graph in Table 5, 50 times. In three different executions, the final solution was 27 and, in other cases, the fitness value was 28. Fig. 9 illustrates the stability of this example. The variance of the obtained solutions was measured to be 0.0575. Hence, it can be highlighted that the proposed method has high stability in achieving the final solution. Also, in different iterations, the proposed method does not produce different and dispersed solutions.

7Я	Fitness
27
26
25
24
23	Run # Iteration
0	10      20      30      40      50

Fig.9. The stability diagram of example 17 in 50 frequent runs

Regarding the problem of discovering the maximum clique, the proposed method and ACO and PS-ACO meta-heuristic methods were investigated and simulated for examples with larger dimensions. The specifications of the instances used in simulating the proposed method, ACO and PS-ACO are given in Table 6. Also, the parameters for simulating the PS-ACO method are given in Table 7.

Table 6. The specification of the larger examples
Example #	# of Nodes	# of Arcs
18	500	11281
19	750	24148
20	1000	45506
21	2500	62733
22	5000	98842
23	10000	147012

In implementing the proposed method by the ant colony algorithm and the combined PS-ACO, each artificial ant starts to go through one of the graph nodes with the larger output degree with respect to the graph’s adjacency matrix. It travels along a route until it reaches the destination (the starting point) without going through duplicate nodes. If all the traversed nodes on the route are connected to each other, the length of the traversed route will be equal to the size of the clique. The justification for starting the movement from a node with the highest communication degree is that the chance and speed of finding the largest clique in the network is enhanced.

Table 7. The simulation parameters of PS-ACO
Parameter	Value	Parameter	Value
α	0.6	to	1
р	0.4	ρ	0.02
c 1	2	w1	0.5
c 2	2	w2	0.5

Table 9. The average computation time (Sec.) of the examples of Table 6

Example #	Metaheuristic Method
	Proposed method	PS-ACO	ACO
18	20.24712	18.44502	25.45140
19	22.01458	21.63179	29.33289
20	27.34115	26.98046	38.46348
21	34.15887	32.20018	49.91205
22	48.22101	45.16672	66.83244
23	61.89466	59.01435	94.34891

The comparison of the simulation results for the metaheuristic methods indicated that the final solution obtained from executing the proposed method was equal to that of the ACO method in one case and better than them in the other cases. Furthermore, it was found that the combined PS-ACO method operates significantly better than the ACO method with respect to solving this problem. The results of the combined PS-ACO method was equal to those of the proposed method with respect to four examples. On the other hand, given the computational time of the simulations, it can be argued that ACO is slower than the other methods and the combined PS-ACO is faster than the other methods in achieving the final solution. Given the two indices of computational time and the value of the final solution, it is obvious that the second index is more significant than the first one because it is considered as the objective function. Consequently, it can be maintained that the proposed method is practically more efficient than the other two methods.

Fig. 10 depicts the comparison of three algorithms in terms of execution time while the problem size increases. In this figure, the horizontal axis denotes the number of nodes in the graph and the vertical axis refers to the computational time in terms of seconds.

Each of the examples given in Table 6 was executed for 10 times. The numerical results of the simulations, including the size of the discovered largest clique in 10 executions are given in Table 8; the average computational time of the methods in seconds is given in Table 9.

Table 8. The largest clique size obtained for examples of Table 6

Example #	Metaheuristic Method
	Proposed Method	PS-ACO	ACO
18	21	21	21
19	25	25	24
20	28	28	26
21	31	30	28
22	34	34	30
23	37	35	31

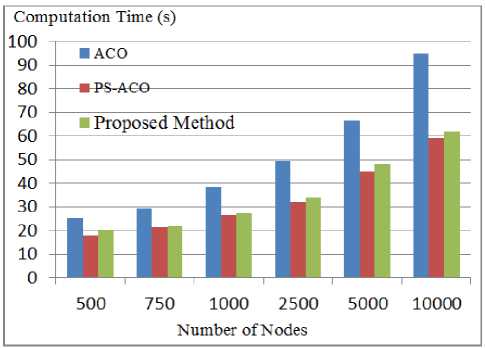
Fig.10. The impact of increasing the problem size on computational time

As shown in this figure, the computational time in the proposed method and the hybrid PS-ACO increases with a milder slope than those of the other methods. When compared with the other two methods, the reason for the slowness of the ant colony is that the artificial ants only pay attention to the amount of the available pheromone on the routes for selecting a route among many routes; they do not use the pheromone information of the entire network. In other words, artificial ants’ decision is only based on local information. Nevertheless, in particle swarm and bee colony methods, in addition to the local information, global information which is gathered by population members is used which leads to the adoption of more efficient decisions. Figures 11 and 12 illustrate the convergence comparison of the simulated metaheuristic methods in achieving the final solution in examples 22 and 23. In these figures, the horizontal axis denotes the number of iterations and the vertical axis indicates the fitness value. These algorithms were duplicated for 150 and 200 times, respectively. Drawing the rest of the figure was ignored due to the lack of improvement of the final solution.

As shown in Fig. 11, the proposed method and the combined PS-ACO had similar convergence and the same final solution; they achieved this value in 112 and 132 iterations, respectively which is regarded as an advantage for the proposed method. The reason for the similarity of the performance of the proposed method and the hybrid PS-ACO is attributed to the similarity of the search method and the use of local and global information in both of these methods. In the proposed method, artificial bees transmit the discovered information to the other bees; in a similar vein, in the hybrid PS-ACO method, artificial ants receive optimal local information from other ants; then, they discover and solve the problem similarly.

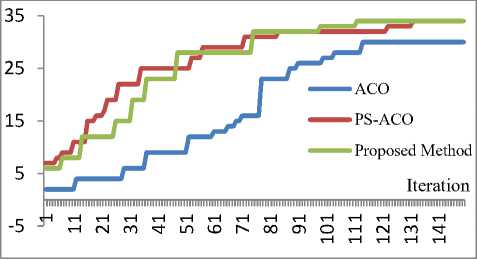
Fig.11. The convergence diagram of example 22

Regarding the example 23, Fig. 12 shows the efficiency of ACO was notably less than those of the other two methods. In this example, whereas the proposed method achieved the final solution of 37 in 192 iterations, the PS-ACO method obtained the final solution of 35 in 166 iterations. This result demonstrates the superiority of the proposed method.

In order to perform a precise assessment, the performance of the proposed method is compared with 8 pioneering heuristics on 5 hard instances using DIMACS popular benchmark. The selected algorithms are IEA-PTS [32], CLS [33], EWCC [34], N/TS [35], ILS [36], AMTS [6], BLS [37] and SBTS [38]. The best obtained and the average clique size (in case the best response is not reached in different executions) are reported in Table 10.

As shown in Table 10, it can be concluded that the proposed method was as successful as other heuristics on all benchmark instances except the large MAN-a45 graph. On C2000.9 and MANN_a45 instances the proposed method has obtained a better average clique size than that of some other heuristics.

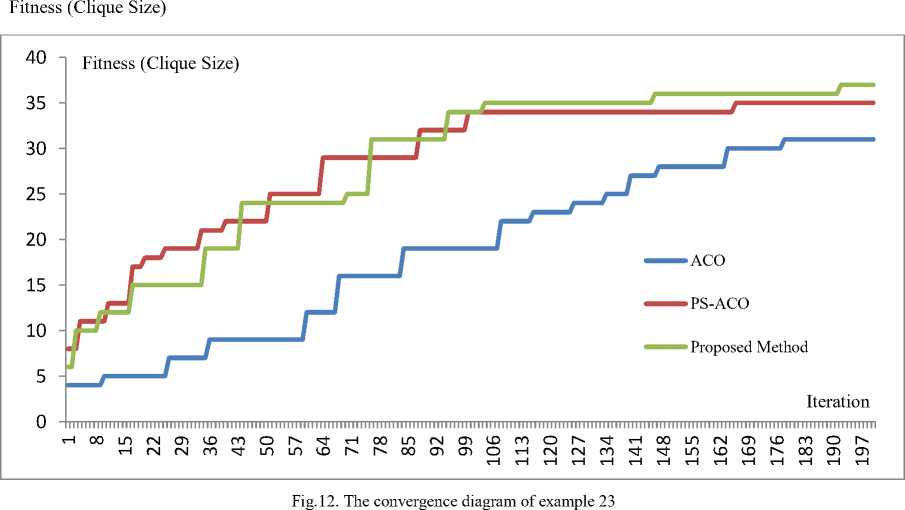
Table 10. The comparison of performance evaluation of the proposed method on DIMACS benchmark instances

Instance Heuristic	brock400_2		Brock400_4		C2000.9		C4000.5		MANN_a45
	Best	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best	Avg.
IEA-PTS	29	27.5	33		79	76.40	18	17.66	345	343.97
CLS	29		33		78		18		344
EWCC	29	25.48	33		79	78.56	18		345	344.94
N/TS	29		33		80	78.37	18		340
ILS	25		33	30.3	77	76.90	18	17.1	345	344.5
AMTS	29		33		80	78.95	18		345	344.04
BLS	29		33		80	78.6	18		342	340.82
SBTS	29		33		80	77.29	18		345
Proposed Method	29		33		80	77.64	18		344	342.89

• V.    Conclusions

In this paper, the maximum clique problem on social networks was investigated and studied. Considering the time complexity of NP-hard nature, we proposed a metaheuristic algorithm based on ABC optimization method for solving the problem. The proposed method was simulated in Matlab on 17 small to medium size standard examples derived from the literature with available optimal solutions, and 6 large-scale examples extracted from the Facebook social network dataset.

The simulation results of the proposed method were compared with the optimal solutions obtained via the deterministic method on the standard examples. It was found that the proposed method, except for an example for which it measured a near-optimal solution, was able to achieve the optimal solutions. For checking the efficiency of the proposed method on large-scale examples, the ACO and the PS-ACO algorithms were also simulated. According to the obtained numerical results, although the computational time of the hybrid PS-ACO is slightly shorter than that of the proposed method, the ABC method was able to achieve better solutions and its convergence speed is also somehow higher than that of PS-ACO. It can be also concluded that the standard ACO method operated weaker than both of the other methods.

Finally, the performance evaluation of the proposed method on some DIMACS benchmarks instances shows the capability of the proposed method obtaining the best-known or near-to-optimal solutions. Besides, the proposed algorithm reaches a better average clique size in comparison with some other heuristics in the literature.