Дискретность земной коры, энергоемкость блоков и сейсмичность европейского севера России

Изучение иерархической дискретности земной коры связано с именами Л. И. Красного [8], М. А. Садовского [15, 16], В. Ф. Писаренко [17] и ряда других исследователей. На основе их исследований создана система структурной организации как Земли в целом, так и отдельных ее регионов. Установлено, что земная кора дискретна и имеет четко выраженное слоистоблоковое строение. Среднее расстояние между границами отдельных геоблоков в системе подчиняется закону, выраженному следующей зависимостью:

L i+1 /L = K ,                  (1)

где К — масштабный коэффициент перехода от одного масштаба блоков к другому (от 2 до 5, в среднем —

• 3 .5), отражающий дискретность земной коры при расчете для ее конкретных структур; L_i — максимальная ширина исследуемого геоблока; L_i+1 — максимальная ширина геоблока следующего порядка.

Как отмечал М. А. Садовский, «разброс значений К указывает на то, что отмечаемое подобие несколько условно и имеет характер статистический » [16, с. 322].

Им было сформулировано положение о том, что геологическая среда всегда находится в критическом энергонасыщенном состоянии, во всяком случае ниже глубины 5—6 км, и основные сейсмические события всегда происходят только по межблоковым структурам [16]. Геомеханики и тектонофизики, изучающие характер деформирования земной коры под воздействием тектонических нагрузок, пришли к выводу, что

сложная блоковая структура верхней части литосферы является результатом распределения диссипированной механической энергии [13]. Различные структуры земной коры приспосабливаются к передаче энергии на более низкие иерархические ступени, вплоть до возникновения некоторого динамического равновесия. Но новая флуктуационная волна энергии, поступающая извне, формирует новое движение, новую организацию. Все это и определяет автомодельные процессы упорядочения структуры, самоорганизацию системы, состоящей из блоков и отдельностей горных пород разного порядка. И поэтому, как полагал М. А. Садовский [15, 16], горную породу можно рассматривать как часть значительно более широких природных открытых систем, способных к самоорганизации за счет энергии, поступающей извне. Т. е. эти структуры находятся в колебательном режиме с меняющимся напряженно-деформированным состоянием.

В свете вышеизложенного актуальным является исследование дискретности земной коры, энергоемкости блоков и плотности разломов, характерных для блоков земной коры, и, как следствие, отражение блоков с разными параметрами в геоморфометрических характеристиках современного рельефа. Необходимо понять, являются ли эти блоки морфоструктурными и можно ли в дальнейшем использовать цифровое моделирование рельефа для их выделения. Авторы в своей работе исходили из положения о сложной структуре разломов как геологических тел. В зависимости от ранга тектонической структуры блоки и трансблоковые зоны сами являются межблоковыми структурами определенного ранга, ограничивающими более крупные структуры земной коры. Блочная структура и наличие выраженных разноориентированных движений индивидуальных и консолидированных блоков приводят к мозаичному, пространственно неоднородному распределению характеристик среды. То есть дискретность литосферы характеризуется сложным сочетанием разных по знаку, направленности и интенсивности тектонических движений, запечатленных в современном строении земной коры. Как следствие, это отражается на таких параметрах, как коэффициент дискретности, значение энергоемкости тектонических структур и индекс расчлененности современного рельефа, а также на сейсмической активности геологических блоков.

Методика исследований

Нами были проведены расчеты коэффициента дискретности для основных мегаблоков Европейского Севера России (Мурманского, Беломорского) и трансблоковых зон (Хибинской и Балтийско-Мезенской), а также узлов их сочленения, выделенных по геологогеофизическим данным (рис. 1). Эти структуры характеризуются максимальным количеством зарегистрированных сейсмических событий (рис. 2).

Коэффициент дискретности, характерный для взаимоотношения блоков разных порядков, рассчитывался по формуле (1). Значения К_ср , характерные для мегаблоков и трансблоковых зон, рассчитывались как среднее арифметическое по формуле (2):

К р = ^i K). (2)

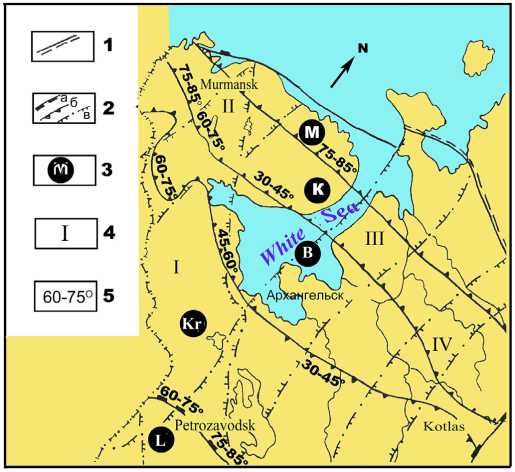
Рис. 1. Схема разломно-блоковой тектоники Европейского Севера России [11]:

• 1    — западная граница Тиманского поднятия; 2 — разломы, ограничивающие: а) геоблоки, б) мегаблоки, в) трансблоковые зоны; мегаблоки и их индексы: М — Мурманский, К — Кольский, B — Беломорский, Кr — Карельский, L — Ладожский; 4 — трансблоковые зоны: I — Ладожско-Баренцевоморская, II — Хибинская, III — Балтийско-Мезенская, IV — Вельско-Цильменская; 5 — расчетные углы падения поверхностей разломов

Fig. 1. Scheme of fault-block tectonics of the European North of Russia [11]:

• 1    — the western border of the Timan uplift; 2 — faults that limit: geoblocks (a), megablocks (b), transblock zones (c); the megablocks and their indices: M — Murmansk, K — Kolsky, B — Belomorsky, Кr — Karelian, L — Ladoga; 4 — transblock zones: I — Ladoga-Barents Sea, II — Khibiny, III — Baltic-Mezen, IV — Velsko-Tsilmenskaya; 5 — calculated angles of fall of fault surfaces

Для расчетов коэффициента дискретности нами использовались карты блокового строения восточной части Балтийского щита [14]. Для территории севера Русской плиты была задействована карта из материалов отчета В. З. Березовского и др. из фондов Архангельского филиала ФБУ «ТФГИ по СЗФО»*. Результаты расчетов приведены ниже.

По геолого-геофизическим данным докембрийский фундамент региона и перекрывающий его плитный покров относятся к двум геоблокам: Карело-Кольскому и Белорусско-Балтийскому [4]. Карело-

Кольский геоблок состоит из четырех мегаблоков (Мурманского, Кольского, Беломорского и Карельского), различающихся по возрасту консолидации, составу докембрийской коры и характеру граничных поверхностей (рис. 1). Зоны сочленения этих мегаблоков обладают повышенной мощностью земной коры (до 50 км) и трассируются не только на территории Балтийского щита, но и в пределах Русской плиты. Блоки более высоких порядков (III и IV) различаются по глубинному строению и структурно-вещественным типам слагающих их комплексов. Границы блоков III-IV порядков представлены линейными зонами разломов [4]. Характерной особенностью региона является наличие трансрегиональных трансблоковых тектонических зон (рис. 2): субмеридиональной Ладожско-Баренцево-морской и северо-восточных — Хибинской, Балтийско-

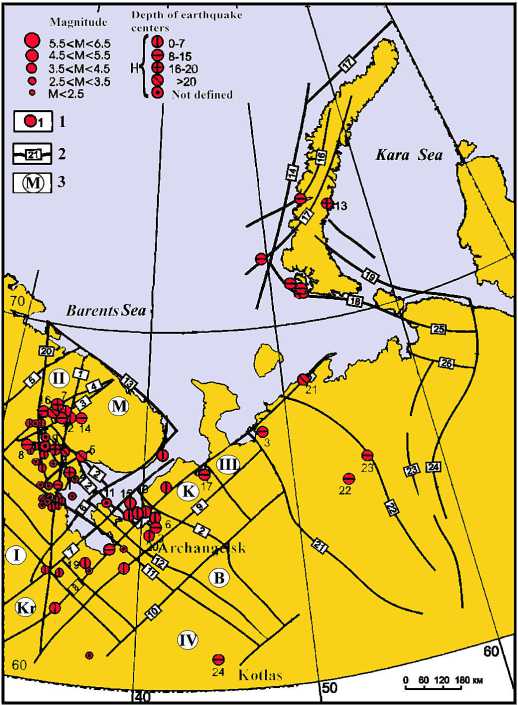
Рис. 2. Карта эпицентров землетрясений севера европейской части России за 1467—1995 гг. (по: [19] с дополнениями).

1 — номера ощутимых землетрясений; 2 — главные разломы; 3 — мегаблоки и трансблоковые зоны и их индексы: М — Мурманский, К — Кольский, B — Беломорский, Кr — Карельский, L — Ладожский; трансблоковые зоны: I — Ладожско-Баренцевоморская, II — Хибинская, III — Балтийско-Мезенская, IV — Вельско-Цильменская

Fig. 2. Map of the epicenters of earthquakes in the North of the European part of Russia for 1467—1995 (by: [19] with add-on). 1 — numbers of tangible earthquakes; 2 — main faults; 3 — megablocks and transblock zones and their indices: M — Murmansk, K — Kolsky, B — Belomorsky, Кr — Karelian, L — Ladoga; transblock zones: I — Ladoga-Barents Sea, II — Khibiny, III — Baltic-Mezen, IV — Velsko-Tsilmenskaya

Мезенской и Вельско-Цильменской, являющихся линейными разломно-блоковыми [4] структурами. Нами было принято условие, что выделенные по высокой сейсмической активности Мурманский и Беломорский мегаблоки, Хибинская и Балтийско-Мезенская трансблоковые зоны являются блоками I порядка.

Результаты расчета дискретности мегаблоков, дополненные расчетами их энергоёмкости, по мнению авторов, позволяют уточнить современную геодинамику земной коры и проявление внутриплитной сейсмичности.

Формула расчета энергоемкости:

^ = I _ З(ЗМ-Е) ^ у + J_. ГМ ² , (3) ^э/с 2 ME ^J 2М \V)

где M — модуль сдвига; E — модуль Юнга; ρ — плотность породы; g — ускорение свободного падения; H — глубина залегания слоя; E_c — сейсмическая энергия землетрясения; V — объем блока.

При умножении на объем мегаблока или трансблоковой зоны получается значение полной энергоемкости исследуемой структуры.

Ниже приведен пример расчета [3]:

Н = 40 км; Е = 7.7·10⁵ кгс/см² = 7.7·10⁸ гс/см²; ρ = 3.38 г/см³ (средняя плотность горных пород земной коры равна 2.8 г /см³); Vs = 8·10⁵см/сек; H = 4·10⁶ см; g = 9.8·10² см/сек²; при этом модуль сдвига М = V_s² ·ρ, ( V_s — скорость поперечной сейсмической волны) ; W_э/с = 9.8·10¹¹ эрг/м³.

Для уточнения структуры вышеперечисленных мегаблоков, трансблоковых зон и узлов их сочленения были рассчитаны поверхностная плотность разломов и функция дробления по А. Н. Колмогорову [7].

Для выделения участков повышенной плотности использовалась схема глубинных структурообразующих разломов под редакцией Д. М. Мильштейна [18] масштаба 1:10000000. Методом прямоугольного «скользящего окна» была подсчитана их плотность (количество разломов) независимо от ранга. Размер «окна» составил 100×100 км с перекрытием в 50 км (для избежания влияния краевых эффектов). Подсчитанные значения присваивались центру «окна». Изолиниями были ограничены участки с одинаковыми значениями. В результате полученные значения определялись как значения поверхностной плотности разломов (10—4 разлом/км2).

Обычно в качестве искомого параметра выбирается характерный размер трещины (на локальном уровне) или «блочность» — характерный размер «блока», высекаемого сетью трещин в монолите [6]. В данном исследовании нами под «блочностью» горных пород понимается совокупность блоков, «высекаемых» ограничивающими их разломами. При поисках теоретической модели для распределения «блочности» активно обсуждается гипотеза логарифмически нормального закона. Эта модель была предложена А. Н. Колмогоровым [7] для результатов дробления горных пород. Она аналитически объясняет возникновение логнормального распределения размеров блоков при дроблении монолита горных пород. В нашем случае суть этой модели излагается по А. И. Иванову [6]. Рассматривается квазиоднородный участок сети разломов (в нашем случае стуктурообразующих) фиксированного ранга в пределах блока. Квазиоднородность означает, что линейная густота разломов в каждом фиксированном направлении подчинена закону Пуассона, параметр λ которого определяется через тензор ориентации трещиноватости на данном участке. Тогда расстояние между соседними трещинами/раз-ломами (L) в этом же направлении распределено по экспоненциальному закону с тем же параметром λ. При выборе трех взаимно ортогональных направлений (простираний) мы получаем три независимых пуассоновских потока. Расстояние в каждом из них между соседними точками деления меняется экспоненциально с параметром λк, (где к = 1, 2, 3), определяемым густотой трещин (разломов) в соответствующем направлении (простирании).

В качестве статистической меры «блочности» ква-зиоднородного участка [6] выступает произведение расстояний между точками деления в направлениях 1, 2, 3 соответственно:

B = L 1 ⋅ L 4 ⋅ L 3 , (4) где В [6] изменяется в интервале 0÷1, так как длины в произведении (4) были масштабированы на единицу.

Выбор такой меры становится понятным, если представить трещиноватость участка как три взаимно перпендикулярные серии трещин с густотами λк, к = 1, 2, 3. Для упрощения длины во всех трех направлениях были масштабированы на единицу [6, с. 365].

При условии, что сомножители распределены по экспоненциальному закону, закон распределения будет иметь следующий вид:

f(S)= 2 Zn ² s. (5)

Формула (5) была нами применена при расчетах функции дробления («блочности»).

Связь сейсмичности с действующими в земной коре и литосфере тектоническими напряжениями общеизвестна. В связи с этим небезынтересно остановиться на анализе изгибных деформаций земной коры. На первой стадии исследования нами были выделены участки (блоки) устойчивого направления максимальной главной кривизны изгибных деформаций, представленной на карте [5] в виде прямых линий. Эти линии были помещены на стереографическую проекцию верхней полусферы сетки Вульфа в азимутах их простираний от направления на север по часовой стрелке. В пределах выделенных участков (блоков) строились сводные розы-диаграммы направлений кривизны из-гибных деформаций, вызванных современными вертикальными движениями земной коры.

Далее нами был проведен расчет отражения структур фундамента в современном рельефе для выделения прямых и обратных форм отражения. Для этого использовалась подготовленная цифровая модель рельефа (ЦМР) ASTER GDEM v.2 и карта поверхности фундамента м-ба 1:1000000 [12]. Более подробно принципы выбора модели, программного обеспечения и методики обработки изложены в работе авторов [10]. Методика расчета описана в работе [12].

Затем был рассчитан индекс расчлененности рельефа на всю территорию Архангельской области. Индекс расчлененности рельефа ( TRI ) служит для объективной количественной оценки изрезанности (неоднородности) рельефа. Значение индекса расчлененности рельефа рассчитывалось по формуле из работы [20]:

TRI = ^\(hZ^^ ,        (6)

где h_0.0 — значение высоты рассматриваемой ячейки ЦМР; h_i,j — значения высот каждой из 8 смежных ячеек.

Чем выше TRI , тем выше среднее квадратичное отклонение высот соседних ячеек от высоты рассматриваемой ячейки, что геометрически интерпретируется как большая расчлененность рельефа. Высота ячейки измеряется относительно некоторого фиксированного уровня, принятого нулевым в зависимости от исходной ЦМР региона, в т. ч. и от уровня моря.

Результаты исследований

Результаты расчетов коэффициента дискретности для основных мегаблоков Европейского Севера России (Мурманского, Беломорского) и трансблоковых зон (Хибинской и Балтийско-Мезенской), а также для узлов их сочленения показали, что исследуемые тектонические структуры и узлы их пересечения характеризуются довольно высокими значениями ( К_мах = 2.32— 2.64). Максимальные значения коэффициента дискретности ( К_мах) в пределах исследуемой территории (рис. 1) характерны для Беломорского мегаблока и Балтийско-Мезенской трансблоковой зоны и, следовательно, узла их пересечения/сочленения. В целом, получены следующие значения коэффициента дискретности: Мурманский мегаблок — 2.53, Беломорский мегаблок — 2.64, Хибинская трансблоковая зона — 2.63, сочленение Беломорского мегаблока и Хибинской зоны — 2.35, сочленение Беломорского мегаблока и Балтийско-Мезенской трансблоковой зоны — 2.42. Таким образом, исследуемые сейсмоактивные зоны (рис. 1, 2) и узлы их пересечения характеризуются высоким коэффициентом дискретности. Много это или мало? Следует отметить, что максимум коэффициента дискретности ( К = 5.0) приходится на такие сейсмотектонические пояса, как Тихоокеанский, Кавказский и др. [1].

Расчеты энергоемкости блоков земной коры в пределах севера Русской плиты [2] показали, что значения W _э/с в пределах сейсмически активного Беломорского мегаблока и Балтийско-Мезенской трансблоковой зоны равны (22—24)·10⁹Дж/м³ при средних значениях (15—17)·10⁹Дж/м³. Аналогичные расчеты были проведены и для хребтов Гаккеля и Книповича в пределах Арктического сейсмического пояса [9]. Значения сдвиговых деформаций хр. Гаккеля варьируют в пределах (24—26)·10⁹Дж/м³; для хребта Книповича — (20— 24)·10⁹Дж/м³. Как видно, значения практически идентичны, что говорит о схожести современных геодина-мических режимов (преобладание растяжения) вышеперечисленных структур [9, 11, 12].

Максимальное значение поверхностной плотности разломов для исследуемого региона достигало 5·10–4, минимальное — 2·10–4 разлома на км2, за исключением отдельных локальных участков, где значения были равны 1·10–4 разлома на км2 (рис. 3, А).

Как видно, наибольшую площадь исследуемой территории занимают участки со значениями поверхностной плотности 3—4·10^–4 разлома на км². Локальные участки с максимальным значением плотности имеют северо-западное и северо-восточное простирания, совпадающие с простираниями Беломорского мега- 19

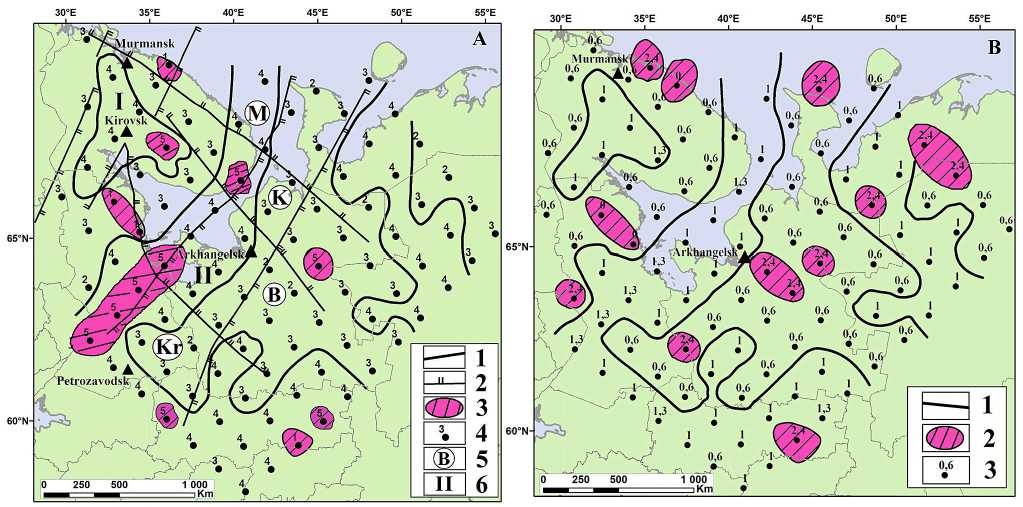
Рис. 3. Карты поверхностной плотности разломов и значений функции дробления («блочности»):

А — карта поверхностной плотности разломов: 1 — изолинии, разделяющие участки различных значений их плотности, в 10—4 разлом/км2; 2 — разломы, ограничивающие мегаблоки и трансблоковые зоны; 3 — участки минимальных и максимальных значений плотности; 4 — суммарное количество разломов в ячейке; 5 — мегаблоки: М — Мурманский, К — Кольский, B — Беломорский, Kr — Карельский; 6 — трансблоковые зоны: I — Хибинская, II — Балтийско-Мезенская;

B — схема значений функции дробления («блочности»): 1 — изолинии значений функции дробления; 2 — участки минимальных и максимальных значений; 3 — значения функции дробления в «окнах»

Fig. 3. Maps of surface density fault and values of the crushing function («blockiness»):

Map of surface fault density (A): 1 — isolines separating areas of different values of their density (10–4 fault/km2); 2 — faults limiting megablocks and transblock zones; 3 — areas of minimum and maximum density values; 4 — the total number of faults in the cell;

• 5 — megablocks: М — Murmansk, K — Kolsky, B — Belomorsky, Kr — Karelian; 6 — transblock zones: I — Khibiny, II — Baltic-Mezen;

Scheme of values of the crushing function («blockiness») (B): 1 — isolines of values of the fault density function; 2 — areas of minimum and maximum values; 3 — values of the crushing function in «windows»

блока Балтийско-Мезенской трансблоковой зоны соответственно. Естественно, полученные данные и не должны быть одинаковыми для всей территории, поскольку плотность характеризует в определенной степени раздробленность участка, выделенного по сумме разломов. В тоже время на схеме глубинных разломов [18] каждый разлом представлен индивидуально, что не дает интегральной площадной характеристики блоков. Идея наших расчетов состояла в том, чтобы выделить участки с максимальной поверхностной плотностью разломов, т. е. откартировать относительно раздробленные участки (блоки). Имея такую карту, можно охарактеризовать те же мегаблоки и морфоструктурные узлы, о которых говорилось выше. К примеру, Беломорский мегаблок, у которого наиболее высокий коэффициент дискретности (2.64), на всем своем протяжении с северо-запада на юго-восток делится на 4 участка с различными значениями плотности разломов. Участки максимальной и минимальной поверхностной плотности чередуются с северо-запада на юго-восток так: 4—5·10^–4, 3·10^–4, 4—5·10^–4, 3—2·10^–4 разлома на км². То же самое можно сказать и о других мегаблоках, только значения поверхностной плотности там другие. Так, сочленение Беломорского мегаблока и Балтийско-Мезенской зоны характеризуется сравнительно высоким значением коэффициента дискретности (2.42), а сочленение того же Беломорского мега- 20

блока с Хибинской трансблоковой зоной — 2.35. Однако по значению поверхностной плотности разломов картина выглядит иначе. В первом случае это значение варьируется от 4 до 2·10–4 разломов на км2, а во втором — 4—5·10–4 разломов на км2. Авторы отдают себе отчет в том, что указанные цифры относительны и зависят от используемой при расчетах детальности схемы глубинных разломов, выделенных по геофизическим данным определенного масштаба, т. е. от ранга анализируемых разломов. Тем не менее в первом приближении они наглядно отражают общую картину для тектонических нарушений и блоков определенных рангов.

На рис. 3, B представлена схема значений функции дробления («блочности»), рассчитанных по формуле (5), в ячейках 100×100 км. Изолиниями разграничены участки различных значений функции. Максимальные значения достигают 2.4, а минимальные — 0 (преобладающие значения — 0.6). В основном значение функции распределения варьируется от 0.6 до 1.3. При сопоставлении двух схем (рис. 3, А и В) видно, что контуры изолиний практически совпадают. Подобное совпадение говорит о том, что подсчет разломов непосредственно по схеме зон глубинных разломов и расчеты функции дробления («блочности») указывают однозначно на одни и те же минимально и максимально раздробленные участки земной коры в пределах исследуемой территории. Это совпадение вполне объяснимо, т. к. при расчетах использовались структурообразующие разломы. Однако на локальном уровне (с наличием аномальных участков) различия все же есть.

По мнению ряда авторов [5, с. 230], «связь сейсмичности с действующими в земной коре тектоническими напряжениями несомненна», и для ее установления продуктивным является анализ тензорных характеристик современных изгибных деформаций.

При анализе характера изгибных деформаций (рис. 4) отмечено, что на исследуемой территории выделяются в основном протяженные зоны северо-западного простирания однонаправленного максимального изгибания блоков земной коры, пространственно совпадающие с Онего-Кандалакшским грабеном, испытывающим активизацию [12] на современном этапе.

Анализ карты направлений максимальной главной кривизны изгибания земной коры в узле пересечения Беломорского блока и Балтийско-Мезенской трансблоковой зоны показал, что максимальные из-гибные деформации здесь отмечаются в азимутах 20— 40° и соответственно 200—220° (рис. 4).

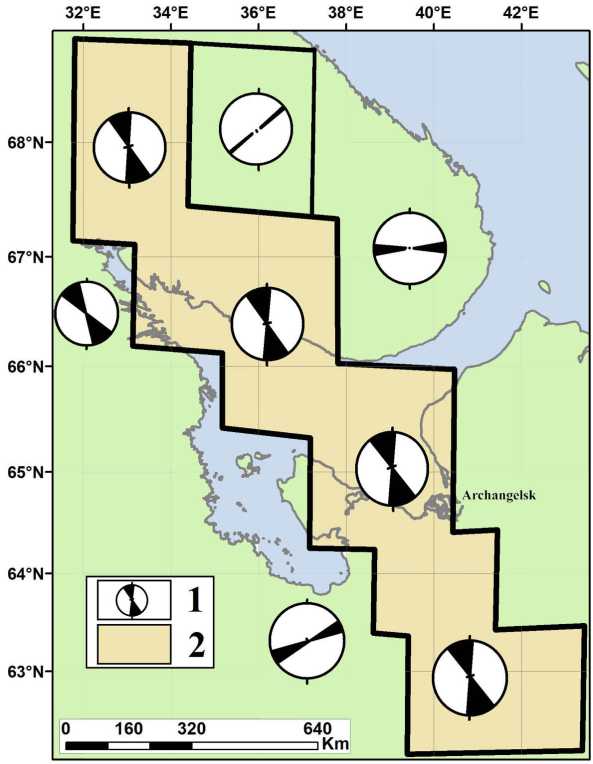
Рис. 4. Сводные розы-диаграммы (в проекции на верхнюю полусферу сетки Вульфа) направлений, вызванных новейшими движениями земной коры:

• 1    — розы-диаграммы; 2 — зона устойчивого максимального изгибания блоков

Fig. 4. Summary rose-diagrams (in projection on the upper hemisphere of the Wolfe grid) directions caused by the latest movements of the earth's crust:

• 1    — rose-diagrams; 2 — zone of stable maximum bending of blocks

Выше было отмечено, что зона максимальных из-гибных деформаций в пределах севера Русской плиты выделяется в северо-западном направлении. Таким образом, сравнивая простирание мегаблока и трансблоковой зоны с ориентацией плоскостей разрыва в групповых механизмах очагов землетрясений, нетрудно заметить, что в случае взброса и взбрососдви-га их направления совпадают [12]. Так, в случае взброса простирание обоих плоскостей ориентировано вдоль Беломорского мегаблока, а в случае взбрососдвига — вдоль Балтийско-Мезенской трансблоковой зоны.

При сопоставлении данных по изгибным деформациям с картой отражения кристаллического фундамента в современном рельефе (рис. 5) отчетливо видно, что узел пересечения Беломорского мегаблока и Балтийско-Мезенской зоны выделяется в обратных формах отражения фундамента, а сама Балтийско-Мезенская зона разделяется на 2 части: обратные формы на юго-западе и прямые на северо-востоке. Беломорский мегаблок характеризуется сложным чередованием форм отражения.

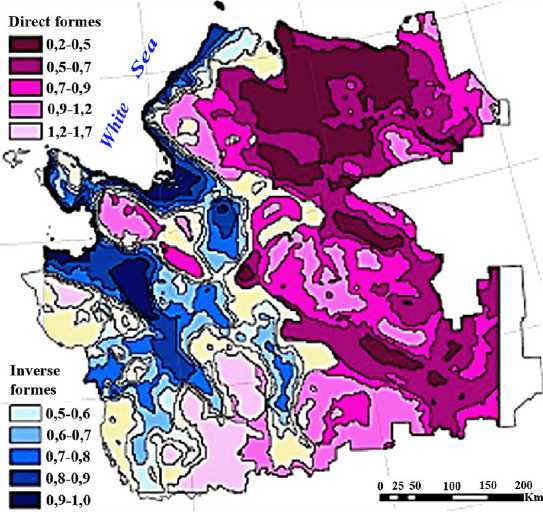
Рис. 5. Прямые и обратные формы отражения структур фундамента в дневном рельефе в переходных и дискретных цветах [12]

Fig. 5. Direct and inverse forms of reflection of foundation structures in the daytime relief in transitional and discrete colors [12]

На карте индекса расчленённости рельефа (рис. 6) вышеперечисленные структуры отражаются достаточно отчетливо, причем пониженными значениями индекса. Это показывает слабую проницаемость для энер-гомассопереноса пород кристаллического фундамента и, соответственно, перекрывающих пород и, как следствие, повышенную способность накопления сейсмической энергии. Наследование структур фундамента в осадочном чехле и структуре поверхности современного рельефа авторами было доказано в более ранних работах [11, 12]. Причем наблюдается тот же характер, что и в отражении фундамента, т. е. Балтийско-Мезенская зона отчетливо разделяется на две части: с пониженными значениями матрицы раз-

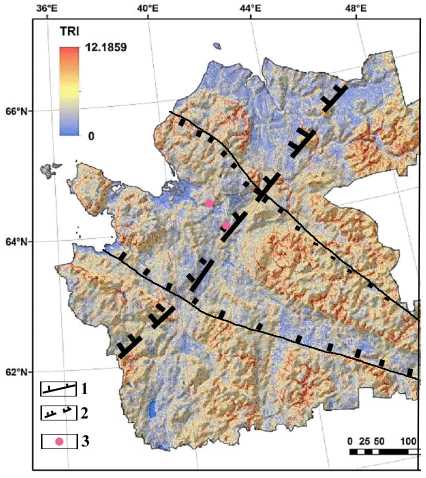
Рис. 6. Индекс расчлененности рельефа (TRI) (размер ячейки 1920 x 1920 м) (по: [12]).

• 1    — граница Беломорского мегаблока, 2 — граница Балтийско-Мезенской трансблоковой зоны, 3 — новые землетрясения, зафиксированные Архангельской сейсмической сетью

  Fig. 6. Terrain Ruggedness Index (TRI) (cell size 1920 x 1920 m) (by: [12]).

1– Border of Belomorsky megablock, 2 — Border of Baltic-Mezen transblock zone, 3 — new earthquakes recorded by the Arkhangelsk seismic network ницы и суммы нормированных высот рельефа дневной поверхности и глубин фундамента на юго-западе и относительно повышенными на северо-востоке.

Выводы

Широко используемые в настоящее время методы изучения приповерхностных структур земной коры, основанные на дискретных измерениях механических параметров (значений дифференциальных движений, различного вида деформаций и их производных) в отдельных участках (блоках), не позволяют получать целостную картину поведения сложноструктурированной геологической среды.

Проведенные нами расчеты показали, что наиболее сейсмоактивные структуры характеризуются повышенными значениями коэффициента дискретности и энергоемкости, т. е. для их активизации нужно минимальное приложение сил воздействия. Согласно карте сопоставления блоковой тектоники (рис. 1) и сейсмичности (рис. 2), основные землетрясения произошли в узле сочленения Беломорского мегаблока северозападного простирания с Балтийско-Мезенской трансблоковой зоной северо-восточного простирания, что подтверждается нашими расчетами.

Значения поверхностной плотности разломов и функции дробления («блочности») говорят о сложном блоковом строении структур, причем участкам с повышенными значениями энергоемкости соответствуют участки с пониженными значения поверх- 22

ностной плотности разломов. Таким образом, это структуры, предрасположенные к накоплению сейсмической энергии.

Сравнивая простирания Беломорского мегаблока и Балтийско-Мезенской трансблоковой зоны с ориентацией плоскостей разрыва в групповых механизмах очагов землетрясений нетрудно заметить, что в случае взброса и взбрососдвига направления их совпадают. Следовательно, можно предположить, что на современном геологическом этапе наиболее подвижным в тектоническом отношении является Беломорский мегаблок. Он же, согласно карте эпицентров землетрясений Европейского Севера (рис. 2), является наиболее сейсмически активным.

Анализ характера отражения структур фундамента в современном рельефе и пространственные особенности распределения значений индекса расчлененности рельефа подтверждают выводы о сложном блоковом строении структур и о разном характере их напряженно-деформированного состояния.

Повышенная поверхностная плотность разломов, дискретность и высокая энергоемкость блоков земной коры, пространственно совпадающая с положением землетрясений, говорят о возможности применения вышеперечисленных параметров для прогноза сейсмоактивных структур. Особенно это актуально для платформенных структур, характеризующихся землетрясениями с малыми магнитудами, не регистрируемыми существующими сейсмическими сетями. Последние результаты Архангельской сейсмической сети, зафиксировавшей новые землетрясения (рис. 6), подтверждают сделанный нами вывод.

Исследование выполнено в рамках государственного задания ФГБУН ФИЦКИА УрО РАН № гос. регистрации АААА-А18-118012390305-7.