Дисперсионные характеристики гибридных волн в ограниченных эллиптических гиротропных областях при продольном намагничивании

Распространение электромагнитных волн (ЭМВ) как в ограниченной, так и в неограниченной продольно-намагниченной гиротропных областях приводит к появлению волн с правым и левым вращением относительно направления намагничивания, совпадающим с направлением распространения. Эти волны имеют разные постоянные распространения, приводящие к вращению плоскости поляризации – эффекту Фарадея. Это свойство широко используется в практических приложениях [1, 2].

В настоящее время распространение ЭМВ в продольно-намагниченных ограниченных прямоугольных и круглых областях достаточно хорошо изучено [1-3]. Но распространение ЭМВ в гиротропных эллиптических областях мало исследовано и носит фрагментарный характер [4].

Целью настоящей работы является вывод дисперсионных уравнений, позволяющих моделировать процесс распространения гибридных ЭМВ в гиротропной эллиптической ограниченной области с бесконечно проводящими стенками в зависимости от напряженности продольного намагничивающего магнитного поля.

Вывод дисперсионных уравнений

Уравнения Максвелла для гармонических процессов без наведенных токов и зарядов имеют вид [1]:

rotH = jw s E ; rotE = — jwB ; divE = 0; divB = 0,

где E , H — соответственно, напряженности электрического и магнитного полей; s — абсолютная диэлектрическая проницаемость среды, s E = D — электрическая индукция, B — магнитная индукции, j — мнимая единица, w — циклическая частота.

При распространении волны в магнитогиротропной среде магнитная индукция B в системе (1) примет следующий вид:

B =1 И H ■

При продольном намагничивании, когда направление внешнего намагничивающего постоянного магнитного поля совпадает с направлением распространения ЭМВ (волна распространяется вдоль координаты Z), тензор магнитной проницаемости феррита, как следует из [1], имеет вид:

где

ww

И = И 0 + И 0 —---2

w ₀ — w

—

IIИ || =

, k = И о

—

И	j K	0
j K	И	0
0	0	И || _

,

wwM

2 w 0

—

2 , w

wM

= и0YM0, Y = 1.76*1011 Кл кг

—

гиромагнитные отношения для спина электрона, w ₀ = И ₀ YH ₀ ферромагнитного резонанса, И ₀ — магнитная постоянная, М ₀

— частота

— намагни-

ченность феррита, Н ₀ — намагничивающее внешнее магнитное поле.

Знаки перед недиагональными компонентами в (3) могут быть проти- воположными, если взять к = — и0

wwM

2 w ₀ ²

—

w ² ■

В системе (1), разложив rotH и rotE по поперечным осям, после подстановок и преобразований в [5] были получены поперечные компоненты электромагнитного поля:

E . =

j y a 2 1 g + g 2 ed

дEz + w c2 dHz _ jw28k ГaEzу aHz д. у a2 дф a2 (дф w8 д.

где

E,„ =	- j y a 2 1		д Ez wt	и c 2 д H z jw 2 kk		(дEz —z - +	У д H z
ф	g + g - ed		_ дф у	a 2 д .      a 2		кд.	w 8 д ф
H. =	j y a 2 1 g + g 2 ed	w s д E z _ у дф		д H z jw 2sk ( w 8 д. + a 2 t У		д ez —- + д .	д H z J дф J_	,
H(n =	- j y a 2 1		w 8 д E z	+ д H z - jw2 8 k	f w 8 д E z		д H z	11
ф	g + g - ed		У д.	д ф     a 2	t у дф		д .	J

. , ф - поперечные координаты эллиптической системы координат,

e - фокусное расстояние эллипса, у - постоянная распространения, d = cah2. - cos2 ф, a2 = w2^118 - у2 = w2^8 - у2, g± = w2ец ± w28k - у2,

2    2 Ц c = w 8--

—

k ²

—

у 2 .

Ц

Подставив (4) в проекции rot H , rot E на продольную ось и используя

divB = 0, получим волновые уравнения гибридных ЕН и НЕ волн соот- ветственно [6]:

д2 EZ д2 HZ

+ ^——Z + e2d2(w28Ц± - у2 EZ - je2d2ywk—HZ = 0, дфЦ

Я2 П        (        и   А

+---Z + e2d2 w28Ц«у HZ + je2d2yw8 — EZ = 0, дф2        (        Ц   J где ц± =

ц ² - k ²

Ц

Для решения волновых уравнений (5) применим метод, предложенный в [7]. Затем, подставив полученные решения в (4) и применив граничные условия в виде Ez = Еф = 0 на бесконечно проводящей внутренней по- верхности ограниченной эллиптической области, получим следующее дисперсионное уравнение:

⁽ ,2     2 ⁴ q 1 '' ⁴ q 2 Ce m ( . 0 , q 1 ) Г ,2     2 ⁴ q 2 ^{1 4} q 1 Ce m ( . 0 , q 2 )

^-1 ^{k 1 -} y —г I ~ 77—77—7⁺l ^k ±^- у —г I —7 ⁺

( e ² J e ² Ce m ( . 0 , q 1 ) I e ² J e ² Ce m ( . 0 , q 2 )

у2 8ka2 Л,Л7 + j и 2 cem (ф, q 2 ) -cem (ф, q 2 ) . у3 w8k "+j Ц 2 cem (ф, q 1 ) л - cem (ф, q 1 ) 1 1=0 (6) - cem (ф, q 1 ) cem (ф, q 1 ) - cem (ф, q 2 ) л cem (ф, q 2 ) 2 где к2 = w2ш2, cem p, q 12) — четные обыкновенные функции Матье I-го рода целого порядка m и их производные cem (р, q12); Cem (^, q 12) - чет ные присоединенные (модифицированные) функции Матье I-го рода (с целым индексом) и их производные Cem (^, q 12), с0- граничный эллипс, e2| к

к 2- Y Y

Л

qi =

функций

4 Матье,

q 2 =

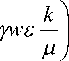
Л 1 ₂        - корни

- параметры уравнения

k2 yws— Л

Ц

+

г

w Ц

V

- ^ Y ц

)w 2ец 2 + у2 Л

- W\\— = 0.

Известно, что в ограниченных эллиптических областях распространя ются четные и нечетные волны [8]. Выражение (6) описывает распростра нение четных волн. Для получения дисперсионного уравнения для нечет ных волн в (6) надо сделать следующую замену:

Ce fe , q 1,2 ) ^ Se fe , q 1,2 ) Ce ( ^ o , q 1,2 ) ^ Se fa» q 1,2 ) , ^ce ( p , q 1,2 ) ^ se ( p , q 1,2 ) ^{ce (} p , q 1,2 ) ^ se ( p , q 1,2 )

где Se(^0, q 1,2), Se'(^o, q 12) - нечетные присоединенные (модифицированные) функции Матье I-го рода (с целым индексом) и их производные, se(р, q 12), se (р, q12) - нечетные обыкновенные функции Матье I-го рода целого порядка m и их производные.

Заключение

На основе впервые полученных дисперсионных уравнений можно получить графики зависимостей постоянных распространения от напряженности подмагничивающего магнитного поля для гиротропной эллиптической области с бесконечно проводящими стенками при продольном намагничивании. Полученные результаты имеют большой практический интерес.