Достаточные условия оптимальности в дискретной иерархической модели

Истоком исследований неоднородных систем можно считать работы Е.А. Барбашина и С.В. Емельянова, Ю.В. Долгоненко, Ю.И. Неймарка, I. Flugge-Lots J. 50-х гг. XX в., а их активное систематическое изучение начато достаточно давно [1-5]. К настоящему времени исследователи разных школ и направлений проявляют к ним все возрастающий интерес в связи с потребностями практики, о чем свидетельствует увеличивающийся поток публикаций [6-10]. Исследования главным образом посвящены системам дифференциальных уравнений переменной структуры (так называемым гибридным). Подобные системы получаются путем различных обобщений самого понятия классической дифференциальной системы. Весьма полное представление об этих исследованиях дают недавние обстоятельные обзоры [11, 12].

Цель данной статьи – продолжение исследований неоднородных систем в рамках альтернативного направления, берущего начало от основополагающей работы В.Ф. Кротова [13], исходя из трактовки неоднородной управляемой системы как конкретизации абстрактной динамической многошаговой системы, для которой в [13] получены общие достаточные условия оптимальности.

На этом пути в [3] была предложена двухуровневая модель дискретно-непрерывной системы (ДНС), на нижнем уровне которой происходят непрерывные однородные процессы, а на верхнем осуществляется дискретное управление их переключениями. Эта модель позволяет систематически учесть изменение не только структуры, но и порядка и даже самой природы однородных подсистем и процессов.

Такая трактовка позволяет эффективно декомпозировать соответствующие задачи управления, прежде всего оптимального управления, на «однородные» подзадачи так, чтобы применить нетрадиционные методы, изложенные в работах В.Ф. Кротова и В.И. Гурмана [14-16] для однородных непрерывных и дискретных систем. Кроме того, как показывает практика [17], нижний уровень может быть представлен и дискретными однородными процессами. В [18] введено понятие абстрактной сети операторов и для нее получены достаточные условия оптимальности как обобщение дискретной динамической модели и достаточных условий [14, 16]. При этом дискретную модель [14, 16] можно рассматривать как частный случай сети – цепочку операторов.

В предлагаемой работе строится новая двухуровневая модель, верхний уровень которой составляет не цепочка, а сеть операторов, а нижний – однородные дискретные управляемые системы. Для этой модели получаются достаточные условия оптимальности. Предварительно напомним понятие сети операторов согласно [18].

1.    Сеть операторов и задача оптимизации

Пусть имеется N операторов произвольной природы fk: Xk x Uk ^ Yk    (yk = f (k, Xk, Uk)).

Вводятся подмножества x_kq , такие что

П П = 1 X kq = X k .

Будем говорить, что выход оператора l подается на вход оператора k , если для некоторого q имеет место равенство x(k , q , x_k ) = y , , где x(k , q , x_k ) — оператор проектирования на подмножество X .

kq

Пусть рассматриваемые операторы соединены указанным образом по некоторой схеме, представленной ориентированным графом (рис.1). Предполагается, что для данного k между номерами q и l имеет место взаимно-однозначное соответствие. Иными словами, Xk олицетворяет множество вхо- дов k-го оператора, занятых в соединениях, а Uk дем называть сетью операторов.

–

множество свободных входов. Такую систему бу-

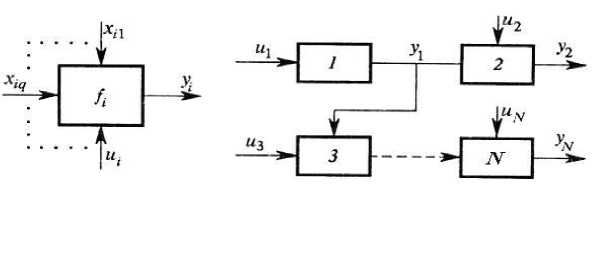
Рис. 1

Описанную сеть можно рассматривать как некоторый оператор

N

F : X ^ Y , X = П U , Y = П Y . e I                   Ie I

Будем называть его оператором следующего верхнего уровня (при сравнении в обратном порядке будем говорить об операторах следующего нижнего уровня ). Такое представление дает возможность отобразить иерархическое строение моделируемого объекта. Специальный случай сети – цепочка произвольных операторов — может рассматриваться как общая модель динамической системы с переменной структурой.

Рассматривается задача о минимуме функционала

NN    N

I = E I k ⁽ Ук ) = E I k ⁽ f ^{( k} , x k , u k )) = E f 0^{( k} , x k , u k )

11    1

на множестве D наборов m = { ( x_k , u_k ) } , k = 1,..., N , связанных указанными соотношениями сети и возможными дополнительными ограничениями вида ( x_k , u_k ) е B ( k ) , где B ( k ) - заданное при каждом k множество.

Требуется найти минимизирующую последовательность { m s } c D , т.е. такую, что I ( m s ) ^ inf I .

2.    Дискретная двухуровневая модель

Предлагается следующая конкретизация указанной абстрактной дискретной модели. Представим условие (xk, uk ) е B(к) в форме xk е X(k), uk е U(к), где X(k) - проекция на Xk, U(к) - сечение B(k) при данных k, xk. Пусть на некотором подмножестве K'c K = {1,...,N} имеем u = (ud,md) , где ud - произвольной природы, а mc- некоторый дискретный управляемый процесс, так что сечение множества U(k, x) при фиксированных x,ud есть допустимое множество Dc(k,x,ud) с соответствующей рекуррентной цепочкой xc (t +1) = fc ( z, t, xc (t), uc (t)),                                (2)

t е T(z), T(z) = ti, ti +1,...,tF xc е Xе(z, t) c Rn(k), uc е Uc (z, t,xc) c Rp(k), z = (k,x, ud).

Оператор правой части (1) сводится к следующему:

Ук = f ^{( k} , ^x , ^u ) = ^ ^{( z} , f ) , Y = ( t i , x | , t F , x F ) е { у^с : t i = t ( z ), x | = ^ ( z ), t F = 3(z ), x F еГ с ( z ) } .

Решением этой комбинированной системы будем считать набор m = ( x ( k ), u ( k )) е D , где при k е K' : u ( k ) = ( u d ( k ), m c ( k )) , m c е D c ( t , x ( k ), u d ( k )) .

Эту модель можно рассматривать как двухуровневую управляемую систему. Нижний уровень для соответствующего оператора представляет собой описание дискретного управляемого процесса, играющего роль управления для верхнего уровня (рис. 2).

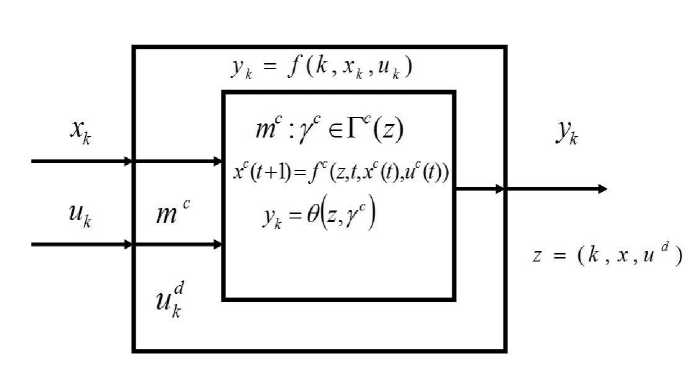
Рис. 2

Задача оптимизации формулируется для верхнего уровня. Достаточные условия оптимальности для нее получаются по аналогии с дискретно-непрерывными процессами [19, 20].

Для номеров k е K ' вводится дополнительно параметрическое семейство (с параметром z ) функций ф : R^{m ( k ) + 1} ^ R . Строится соответствующая модификация обобщенного лагранжиана [19, 20]:

L = - £ R k - £ R k . где

K \ K'       K •

R k ( x . u ) = £ ( ф ( k . l . f ( k . x . u )) - ф ( l . k . x( k . l . x ))) — f ° ( k . x . u ) .

i = 1

i = 1

G (z. Y) = £ (ф( k. l. y„) - ф( l. k. x( k .j. xt))) + ф (z. t,. x?) - l=1

R^c ( z . t . x^c . u^c ) = ф ( t + 1. f^c ( z . t . x^c . u^c )) - ф ( z . t . x^c ) .

ц c (z. t) = sup {R c : xc е X c (z. t). u е U c (z. t. xc)}, где yk = 6(z. уc) при K е K'. yk = f (k. x. u) при k е K \ K'. Обозначим

Ц(k ) = sup{ G ( z . Y ): Y е Г ^c ( z ). x , е X^c ( z . t , ) .

Легко убедиться. что L ( m ) = I ( m ) при m е D . т.е. при выполнении отброшенных связей. Для этого сначала рассмотрим выражение для функции R^c . При выполнении рекуррентной цепочки в (2)

-ZRc (z. t. xc. uc ) + фС (z. t,.x,) - ^ (z. tF. xF) = tI tF -1

= -Z (Фс (t + 1. x (t +1)) - ^ (z. t. xc (t))) + ^ (z. t,. xc) -tI c             c              tF c           c             c           c

- ф ( z . t F . x f ) = - Z (Ф ( z . t . x ( t )) - ф ( z . t . x ( t )). t_I

N                                         t F - 1                               t F - 1

£ ^R k = ££ ⁽ ф ^{( k} . ^l . y_k ) - ф ⁽ k . ^l . y_t )) ⁺Z ^{ц ( z} . t ) ^{- ,} k ⁽ Ук ) ^-Z ^{ц ( z} . t ^{) .}

K '             K ' l = 1                                                    t ,                                        t ,

Тогда

N

£ ^R k = ££ ⁽ ф ⁽ k . ^l . Ук ) - ф ⁽ k . ^l . У1 )) ^{- ,} k ⁽ Ук ) .

K'            K' l = 1

Окончательно имеем

N Г                                 ^

^-£ I ф ( k . ^l . x^(l )) ^- ф ( k . ^l . x ( k )) ⁺£ ^, k ⁽ Ук )

k . l = 1 V                                            k = 1            7

= , .

L=-£ Rk-£ Rk

K \ K'        K'

Отсюда непосредственно вытекает следующая теорема.

Теорема 1. Пусть имеются последовательность элементов {ms}с D и пара (ф.фc) такие, что:

• 1.    R ( k , x s ( k ), u s ( k )) ^ ц( k );

• 2.    Z ( R ( Z s ( k ) t , X s ( k , t ) , U s ( k , t ) ) - ^ ( Z s ( k ) , t ) ) ^ 0 - k ^e K t_I

• 3.    G ( Z s ( k ), r : ( k ) ) - ^ '( k ) ^ 0 , k e K'.

t F ^{- 1}

Тогда последовательность { m s } минимизирующая для I на D.

Полученные общие достаточные условия могут быть использованы для разработки конкретных методов и алгоритмов оптимизации управления в сложных системах, моделируемых как сети операторов. При этом может быть использован опыт исследования моделей, рассматриваемых как частные случаи сети операторов: динамической ДНС, дерева операторов [21], моделирующего, например, дискретизованное распределение гидрохимических компонентов в бассейне реки.

Заключение

Предложенная модель на основе абстрактной сети операторов является переходом от чисто динамических неоднородных систем к более общему классу систем сетевой структуры.

Заметим, что рассматриваемая на нижнем уровне дискретная однородная подсистема может быть получена в результате естественной дискретизации непрерывной системы на этапе вычислений. Такая схема для динамических неоднородных систем реализована в [22]. Это существенно расширяет область приложений иерархического представления.

Изложенный подход к исследованию и оптимизации неоднородных процессов позволяет декомпозировать соответствующие задачи управления на задачи для однородных подсистем, что позволяет рассматривать широкий круг сложных прикладных задач.