Достоверность среднего балла как результата ЕГЭ (на примере экзамена по математике в Республике Мордовия в 2010 г.)

С 2009 г. в России в качестве формы государственной (итоговой) аттестации обучающихся, освоивших образовательные программы среднего (полного) общего образования, установлен Единый государственный экзамен — ЕГЭ [6]. Будучи совмещенным выпускным и вступительным испытанием, ЕГЭ представляет собой важное средство диагностики качества обучения в каждом учебном заведении, регионе и стране в целом, поэтому большое значение приобретают статистическая обработка и анализ результатов экзамена по каждому из предметов.

Один из этапов обработки результатов экзамена — выявление в регионе образовательных учреждений с наиболее высоким (или низким) качеством преподавания той или иной дисциплины. Очевидным критерием качества подготовки в школе (лицее, техникуме и т. д.) является средний тестовый балл, полученный ее выпускниками за ЕГЭ. Однако возникает вопрос: насколько данный критерий достоверен? Попытаемся ответить на этот вопрос, проанализировав результаты ЕГЭ по математике в Республике Мордовия в 2010 г. [5].

Логично предположить, что лучшие результаты по математике будут показаны выпускниками лицеев, имеющих физико-математическую специализацию, но статистика дает несколько иную картину (таблица).

Итак, в десятку лучших школ вошли всего два лицея (выделены курсивом), причем они оказались не в верхних стро ках таблицы. Остальные восемь школ — сельские, большей частью малокомплектные. Для сравнения: в городских учебных заведениях ЕГЭ по математике сдавали 31 (лицей № 4) и 67 (лицей № 43)учеников.

Школы с наиболее высокими средними баллами по математике

№ п/п	Название школы	Средний балл
1	Вадово-Селищенская СОШ	69,00
2	Поводимовская СОШ	67,83
3	Лицей № 4 г. о. Саранск	67,13
4	Акчеевская СОШ	67,00
5	Ардатовская СОШ	66,00
6	Анаевская СОШ	66,00
7	Гуляевская СОШ	65,50
8	Дубенская СОШ	64,79
9	Лицей № 43 г. о. Саранск	64,55
10	Новокарьгинская СОШ	64,50

Именно малочисленностью выпускников объясняется их «высокий» результат. Так, средний балл в Вадово-Сели-щенской, Ардатовской и Анаевской школах (позиции 1, 5 и 6) позволяет утверждать, что в них экзамен по математике сдавал всего один ученик. Дело в том, что результаты участника ЕГЭ сначала оцениваются так называемыми первичными баллами, которые затем по определенным правилам переводятся в 100-балльную шкалу. Итоговые оценки, равные 69 и 66, соответствовали (по шкале 2010 г.) 16 и 15 первичным баллам. Если в данном учебном заведении ЕГЭ сдают несколько человек, вероятность

того, что их средний балл будет целым числом, да еще соответствующим целому числу первичных баллов, крайне м ала.

Далее, с большой долей уверенности можно предположить, что в Акчеевской, Гуляевской и Новокарьгинской школах ЕГЭ по математике сдавали не более 3— 4 выпускников: средний балл в этих учебных заведениях либо целый (но не соответствующий какому-либо первичному), либо полуцелый.

С математической точки зрения результат экзамена в каждом образовательном учреждении можно рассматривать как случайную величину X, у которой требуется оценить математическое ожидание M(X) = а. Исходной информацией для статистического исследования служит выборка x_p..., x n — результаты, показанные n выпускниками этого учреждения. Известно, что точечной оценкой для а является выборочное среднее

_ X1 + ... + xn x =-----.

n

Как было показано выше, само по себе значение x характеризует выборку не полностью. Более полную информа цию о значении а предоставляет доверительный интервал (amin; a max). Принято считать, что он накрывает а с достоверностью Y, если с вероятностью у выполнено неравенство amin < а < amax. Как правило, доверительный интервал для мате матического ожидания записывается в виде, симметричном относительно выбо рочного среднего:

a min = x — А, a ma _x = x + А,

где А — половина ширины доверитель ного интервала, зависящая от заданной достоверности у и объема выборки n.

Чем больше у и чем меньше n, тем больше А. Другими словами, чем выше требования к достоверности оценки и чем меньшей исходной информацией мы обладаем, тем шире доверительный ин тервал.

Интерес представляет следующая задача: найти такой объем выборки n, чтобы при заданной достоверности у доверительный интервал имел заданную ширину 2А. Применительно к итогам ЕГЭ требуется определить, каким должно быть число выпускников школы, чтобы средний балл ЕГЭ x мог выступать достоверной характеристикой достигнутых ею результатов. При решении этой задачи необходимо знать закон распределения величины X, ибо вид функции A(n, y) будет меняться. Кроме того, надо определить, какие значения у и А взять в качестве исходных.

Для подробного анализа распределения X нужны сведения о результатах каждого выпускника в каждом учебном заведении, однако такая информация в открытом доступе отсутствует. Для упрощения предположим, что результаты ЕГЭ во всех образовательных учреждениях относятся к тому же типу случайной величины, что и общереспубликанские результаты. Тогда на основе отчета о результатах ЕГЭ [5] можно установить распределение баллов по республике в целом, а специфику конкретных школ и лицеев при необходимости учитывать с помощью изменения параметров уже найденного закона распределения.

Число участников ЕГЭ 2010 г. по математике, набравших то или иное количество баллов, приведено на рис. 1.

Несмотря на асимметрию гистограммы, наличие резко выраженного пика позволяет выдвинуть гипотезу о нормальном распределении X.

Существует много критериев проверки таких гипотез, из которых самым точным является критерий согласия х². К сожалению, форма представления исходных данных не позволяет его использовать. Диапазон изменения X — от 0 до 100 баллов — разбит в отчете на 10 интервалов, что для N = 4 563 элементов генеральной совокупности (таково общее число участников ЕГЭ) совершенно недостаточно [3]. По известной формуле Стерджеса, количество интервалов к оценивается величиной 1 + log ₂ N; при указанном объеме выборки оно должно составлять 13—14. При N > 200 эффективна более сложная оценка, согласно которой к = 110. В связи с этим были использованы два приближенных критерия.

Число выпускников, чел.

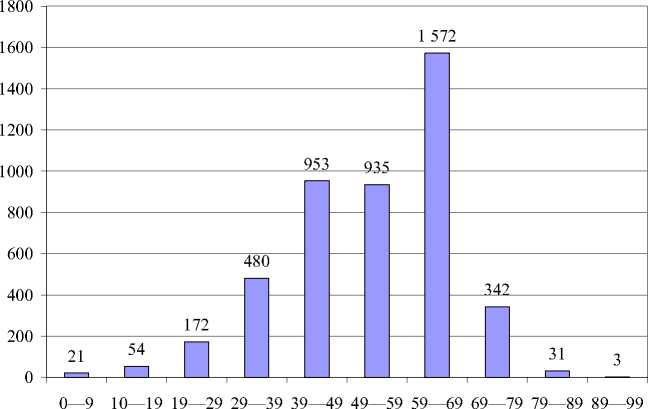
Количество баллов

Р и с. 1. Распределение баллов ЕГЭ по математике

Первый из критериев основан на методе спрямляемых диаграмм [2]. Он является графическим: требуется проверить, лежат ли точки, координаты которых получены по определенным правилам на основе имеющихся данных, дос таточно близко к некоторой теоретической прямой. Применение этого метода, т. е. сравнение теории с эмпирическими данными, показало, что точки действительно группируются возле прямой (рис. 2).

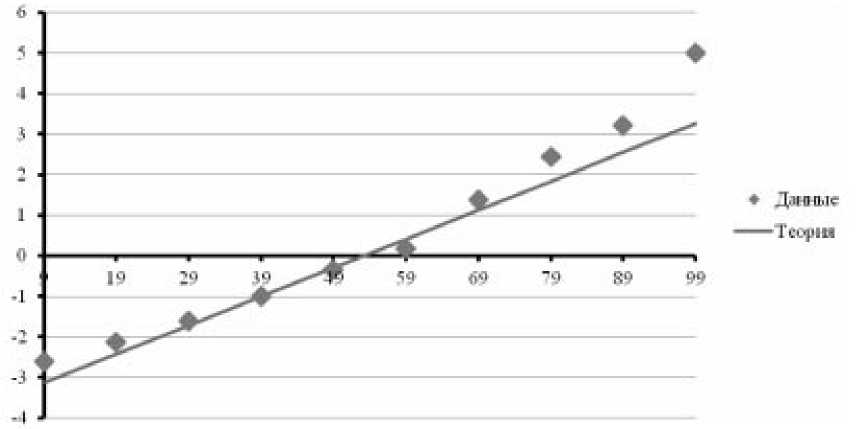
Р и с. 2. Использование метода спрямляемых диаграмм для проверки гипотезы о нормальном распределении баллов ЕГЭ

Второй критерий основан на следующем факте [4]. Если случайная величина имеет нормальное распределение с математическим ожиданием а и средним квадратическим отклонением о, то:

• а)    вероятность попадания величины в интервал (а - 0,625о, а + 0,625о) приблизительно равна 46,80 %;

• б)    вероятность попадания величины в интервал (а - о, а + о) приблизительно равна 68,27 %;

• в)    вероятность попадания величины в интервал (а - 2о, a + 2о) приблизительно равна 95,45 %;

• г)    вероятность попадания величины в интервал (а - 3о, а + 3о) приблизительно равна 99,73 % (правило «3о»).

При использовании второго критерия наряду с выборочным средним x = 53,24 была найдена точечная оценка для о — исправленное выборочное среднее квадратическое отклонение о = 14,07. После этого в условиях а) — г) величины а и о были заменены на x и s, а вероятности — на доли числа работ, оцененных соответствующими баллами, от их общего количества. Было установлено, что условия в) и г) выполняются почти точно, а в условиях а) и б) отклонение эмпирически полученных вероятностей от теоретических не превышает 7,6 %.

По мнению авторов, результаты использования обоих критериев позволяют утверждать, что распределение величины Xв целом по республике близко к нормальному.

Если среднее квадратическое отклонение о известно, а случайная величина распределена нормально, то зависимость A(n, у) такова:

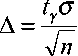
где t — корень уравнения 2Ф( t ) = у, Ф(t) — функция Лапласа [1; 2; 4].

Отсюда

n =

(^ 1 ²

A

.

V 7

Сделаем еще одно упрощение: будем считать, что во всех образовательных

учреждениях значение о одно и то же и равно среднему по республике показателю. Для Мордовии в целом можно принять о = s = 14,07 (объем общереспубликанской выборки велик, и разница между теоретическим значением о и эмпирической величиной s весьма мала). Теперь требуется задать полуширину доверительного интервала A, выбрать достоверность у, и задача будет решена — останется подставить известные параметры в правую часть уравнения (1).

При определении A будем исходить из следующих соображений.

Пусть случайные величины X и Y — результаты экзаменов в двух школах; по выборочным средним баллам x и у требуется оценить математические ожидания M(X) и M(Y соответственно. Если разница между x и у меньше 2A, доверительные интервалы ( x - A; x + A) и ( у - A; у + A) будут пересекаться. В таком случае M(X) и M(Y) могут ^казаться равными, т. е. различие x и у незначимо — оба учебных заведения демонстрируют примерно одинаковый уровень подготовки выпускников.

Величина A должна быть такой, чтобы надежно отличать «лучшие» (по итогам ЕГЭ) школы от среднестатистических. Обозначим через X R средний балл по региону. Выберем учебное заведение, высокий результат которого не вызывает сомнений; его средний балл обозначим X Если теперь положить

A = 1/3 (X (₊) - X r ), (2) то доверительные интервалы для баллов «средних» и «лучших» школ не будут пересекаться (рис. 3).

X R ^A , ^A , ^A X (+), «Средние» школы «Лучшие» школы

Р и с. 3. Разграничение результатов среднестатистических и «лучших» школ

Согласно данным Министерства образования РМ [5], в 2010 г. на экзамене по математикеX R = 53,24. В качествеX (₊) можно выбрать средний балл лицея № 4: X = 67,13. Число участников ЕГЭ из этого учебного заведения (31 чел.) делает указанный результат неслучайным. Тогда A = (67,13 - 53,24)/3 = 4,63.

Аналогично A может подбираться так, чтобы отделить «средние» учебные заведения от «худших». Тогда вместо X (₊) следует выбрать достоверно низкий результат X. Если в качестве эталона взять вечернюю (сменную) общеобразовательную школу № 44, то X = 33,96 и A = (53,24 - 33,96)/3 = 6,47.

Из двух полученных значений A (4,63 и 6,47) логично выбрать меньшее.

Если теперь положить достоверность Y = 0,7, то согласно формуле (1) n = 10 (результат округлен до ближайшего большего целого). Следовательно, при анализе результатов ЕГЭ в конкретных учебных заведениях нужно рассматривать лишь те, в которых не менее 10 выпускников.

Необходимо учесть, что в формулу (1) входят два параметра — t и А, — в равной степени влияющие на значение n. При этом для повышения достоверности оценки 1 требуется увеличивать, что ведет к повышению объема выборки n. С другой стороны, ограничение, наложенное на А формулой (2), может быть слишком жестким: достаточно, чтобы выполнялось неравенство X - X_R > 2А. Увеличивая А, мы будем уменьшать n. Так, при А = 4,63 (первоначальное значение) и Y = 0,95 величина n возрастает с 10 до 36. В Мордовии не слишком много школ с таким числом выпускников, а это значит, что из анализа будет исключено большое количество учебных заведений. Напротив, при А = (X (₊) - X_R)/2 = 6,945 и Y = 0,7 получается, что n = 5. Однако невысокое значение у вкупе с тем, что доверительные интервалы для «средних» и «лучших» школ плотно примыкают друг к другу, снижает ценность прогнозов для учебных заведений с 5—6 выпускниками.

Варьируя сразу у и А, можно добиться уменьшения n при одновременном повышении достоверности. Нижним порогом, при котором среднему баллу в конкретном учебном заведении еще можно доверять, является численность выпускников не менее 7—8 чел.

Итак, критерием достоверности результата ЕГЭ является количество учеников школы, принявших участие в экза мене. В статье предложен способ, позволяющий определить искомое количество и основанный на отделении «лучших» и «худших» школ от среднестатистических. Указанный метод является гибким инструментом анализа достоверности среднего балла, так как учитывает особенности каждой конкретной задачи. В частности, в изученном случае (ЕГЭ 2010 г. по математике в Республике Мордовия) искомое число выпускников школы должно быть не менее 7—8 чел.

СПИСОК

ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

• 1.    Бакаева, О. А. Определение минимального объема выборки / О. А. Бакаева // Вести. Мордов. ун-та. Сер. Физико-математические науки. — 2010. — № 4. — С. 111—114.

• 2.    Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учебное пособие для студентов вузов / В. Е. Гмурман. — 9-е изд., стер. — Москва : Высш. шк., 2004. — 404 с.

• 3.    Кобзарь, А. И. Прикладная математическая статистика. Для инженеров и научных работников / А. И. Кобзарь. — Москва : ФИЗМАТЛИТ, 2006. — 816 с.

• 4.    Лапач, С. М. Статистические методы в медико-биологических исследованиях с использованием Excel / С. М. Лапач, А. В. Чубенко, П. М. Бабич. — Киев : МОРИОН, 2001. — 408 с.

• 5.    Министерство образования Республики Мордовия [Электронный ресурс] : [Официальный сайт]. — Электрон. дан. и прогр. — Режим доступа: http://mo .edurm.ru/informs/obr_nadzor/ege/ otcheti/mat.doc, свободный. — Загл. с экрана. — Дата обращения: 26.06.2012.

• 6.    Федеральный закон № 17-ФЗ от 09.02.07 «О внесении изменений в закон Российской Федерации «Об образовании» и Федеральный закон «О высшем и послевузовском профессиональном образовании» в части проведения единого государственного экзамена» [Электронный ресурс]. — Введ. 2007-02-19 // КонсультантПлюс : справочно-правовая система. — Электрон. дан. и прогр. — Загл. с экрана.

Поступила 23.08.12.