Два алгоритма на основе техники стохастического градиентного спуска для рекомендательных систем
Автор: Никулин В.Н., Прозорова Т.Г.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (26), 2014 года.
Бесплатный доступ
Рекомендательная система - это область машинного обучения, целью которой является создание алгоритмов для определения пользовательских предпочтений на базе известных оценок или поведения пользователя в прошлом при выборе или приобретении товаров. Применение таких систем в спорте, маркетинге и образовании имеет большое значение. Основной интерес применения таких систем в образовании состоит в улучшении методов оценивания студентов, состоящих в прогнозе, ответит ли студент правильно на следующий вопрос. Такие прогнозы могут помочь студенту правильно сориентироваться и определить ту область знаний, на которую следует обратить особое внимание. Заметим, что имеющиеся данные представлены в форме списка, а не в традиционной матричной форме, следовательно, стандартная техника факторизации здесь неприменима. При обработке данных, в которых большая часть значений целевой функции неизвестна и требует прогнозирования, хорошо себя зарекомендовали стохастические градиентные методы. В данной работе рассмотрена оптимизация таких наиболее значимых вариативных параметров, как количество факторов, параметры обучения и регулирования, число глобальных итераций. Исследования и эксперименты базируются на данных, которые использовались при проведении международных соревнований по анализу данных Grockit и Chess на платформе Kaggle.
Матричная факторизация, коллаборативная фильтрация, рекомендательная система, online-обучение, шахматные рейтинги, попарные сравнения, обучение без учителя
Короткий адрес: https://sciup.org/14729923
IDR: 14729923 | УДК: 004.9
Текст научной статьи Два алгоритма на основе техники стохастического градиентного спуска для рекомендательных систем
В последнее время модели на основе независимого компонентного анализа и неотрицательной матричной факторизации (NMF: non-negative matrix factorisation) стали популярными темами для исследования вследствие их очевидной полезности [1]. Следует отметить, что факторные переменные не являются явными в том смысле, что не используется никаких предварительных знаний о переменных за исключением таких общих качеств,
как гауссовость, статистическая независимость или неотрицательность.
Примерами методов успешных матричных факторизаций являются сингулярное разложение и неотрицательное матричное разложение [2]. Кроме того, разработан новый, очень быстрый алгоритм матричной факторизации на основе метода градиентного спуска (GMF: gradient-based matrix factorisation), который представлен в наших предыдущих статьях [3] и [4].
Основным предметом данной статьи является более специализированная версия алгоритма GMF. Название нового алгоритма LF+SGD: list factorization plus stochastic gra- dient descent. Главной особенностью алгоритма LF+SGD являются два обучающих параметра в соответствии с числом факторных матриц. По определению процесс обучения включает регулирование как неотъемлемый компонент.
Заметим, что метод стохастического градиентного спуска (SGD) является особенно эффективным в том случае, когда целевая функция представляет собой сумму большого числа элементов со многими переменными параметрами. Другим примером применимости стохастического градиентного спуска служит историческая последовательность шахматных партий за период более десяти лет (см. раздел 3). Следует заметить, что основная идея алгоритма, представленного в разделе 3.1, опубликована в работе [5].
1. Факторизация списков на основе техники стохастического градиентного спуска (LF+SGD)
В соответствии с [6] в этом разделе используются следующие обозначения. Матрица рейтингов обозначается как X е { 0,1 } I х J , где значение x j = 1 показывает, что i- й студент правильно решил j- ю задачу и x j = 0 в противном случае. I и J – общее количество студентов и задач соответственно. Верхний индекс «крышка» обозначает прогнозируемое значение заданной величины: x – прогнозируемое значение x .
Количество студентов I обычно измеряется сотнями тысяч, количество задач J – тысячами. Данные представлены в матрице рейтингов X размера I х J , которая является разреженной в связи с тем, что большинство значений неизвестно. Обозначим множество известных пар ( i , j ) матрицы X как ^ . Нашей целью является нахождение небольшого числа факторов или метастудентов K << min( I , J ). Затем исходная матрица оценок может быть представлена как линейная комбинация этих метастудентов и метазадач. Математически это соответствует представлению матрицы X в виде произведения двух матриц
X» AB , (1)
где весовая матрица A имеет размеры I х K , факторная матрица B - K х J , каждая из K строк представляет собой прогноз того, как метастудент справится с соответствующей метазадачей.
Главной особенностью стохастического градиентного спуска является отсутствие требования представления входных данных X в матричной форме. Фактически приведенный ниже алгоритм работает не с матрицей, а со списком данных.
Отметим, что формула (1) является не точным, а приблизительным соотношением, где последовательные прогнозируемые величины для элементов (i, j) рейтинговой матрицы X вычисляются по формуле xj =------1------, (2)
J 1 + exp( - s j )
K где sij =E aikbkj.
k = 1
Задача состоит в максимизации следующей функции потерь (биномиальное отклонение):
L ( A , B , ^ 1 , M 2 ) = „ ^ H ij ,
# Л ( i , j ) еШ
KK
Hj= Ej + «Sa + M2Zbj (4)
ln(10) k = 1 k = 1
E ij = - x ij ln( x ij ) - (1 - x ij ) ln(1 - x ij ) , (5)
где M d > 0 , d = 1,2 — регулирующие параметры.
Приведем алгоритм LF+SGD с квадратичной регуляризацией.
Шаг 4 (внутренний цикл по факторам) . Для k от 1 до K выполнить шаги 5–12.
Шаг 5 . а = a ik b kj .
Шаг 6 . a ik ^ a ik - Л 1 ( А • b j + ^ 1 a ik ).
Шаг 7 . S ^ S - а + aikbk, , pr =---------- .
k 1 + exp( - S )
Шаг 8 . А = x ^ - pr .
Шаг 9 . а = a ik b kj .
Шаг 10 . b j ^ b j - Л 2О a ik + ^ 2 b j ) .
Шаг 11 . S ^ S - а + aikbk, , pr =----------- .
ik k 1 + exp( - S )
Шаг 12 . А = x ^ - pr .
Результат : A и B – факторные матрицы.
E j = - x ij ( s j
—
ln(l + exp( s ij ))) +
имеют сле-
(7а)
(7б)
Международное соревнование Grockit проводилось на платформе Kaggle1 с 18 ноября 2011 г. по 29 февраля 2012 г. (всего 103 дня). Использованный нами алгоритм продемонстрировал 15-й результат из 241. Описание метода победителя приведено в [7].
Grockit2 – это компания социального обучения, которая создает инструменты на базе Интернета, помогающие студентам учиться друг у друга. Основной задачей Grockit является обеспечение студентов гибким графиком обучения. Успех Grockit непосредственно зависит от успехов студентов.
Grockit – это мировой быстроразви-вающийся сервис online-тестирования для людей, стремящихся улучшить свои результаты как на стандартных тестах, так и на тестах, необходимых для поступления в колледж.
Grockit – это адаптивная, персонализирующая обучающая программа, известная своими уникальными социальными особенностями, которые помогают людям быстро изучать новые области и достаточно корректно отвечать на вопросы. Обучение доступно online в любое время дня, из любого места, где имеется Интернет. Grockit предсказывает оценку студентов на базе их ответов и хода процесса обучения. Персонализация и независимое обучение также очень важны. План обучения Grockit предполагает практические тесты, ориентированные на те области знания, в которых обучающиеся довольно слабы, а хорошо спроектированный автоматический репетитор поможет освоить необходимые знания гораздо быстрее.
Функция Grockit.TV используется для демонстрации заслуженными преподавателями методики решения задач, которые могут быть применены в процессе обучения. Это как в популярной компании Facebook, но только для обучения. Комбинируя социальное взаимодействие с обучением, Grockit поощряет академический успех через взаимодействие с другими обучающимися.
Поставив целью организовать занятия студентов в различной форме, компания создала центр online-взаимодействия, где студенты могут помогать друг другу в выполнении домашнего задания, развивая тем самым,
-
1 URL: http:// www.kaggle.com
-
2 URL: https://grockit.com
важные в XXI в. качества кооперации. Выбранные для себя тесты можно выполнять индивидуально или в составе команды. Социализированное обучение позволяет многим студентам значительно улучшить знания.
Становление Grockit потребовало капитала. Компания привлекла 17 млн долл. в качестве инвестиций на протяжении своего существования. Венчурными инвесторами были и являются в настоящее время Benchmark Capital, Atlas Ventures и Integral Capital Partners и индивидуальные инвесторы Марк Пинкус (Zynga CEO) и Рид Хоффман, председатель LinkedIn's (LNKD).
Частью пути развития Grockit было включение в процесс получения знаний стимулирующего элемента развлечения (через сетевое социальное взаимодействие) как очень существенного элемента обучения. Когда люди работают над заданиями, они могут отправить мгновенное сообщение другим людям с целью получения совета или просто вести диалог через панель в правой части окна. Это общение не производит никакого звука, поэтому не является слишком навязчивым, но и не позволяет полностью изолироваться и расслабиться.
Grockit поощряет вежливость людей в общении, так как все разговоры сохраняются. Кроме того, люди могут помечать флагами других пользователей, которые используют некорректные высказывания. Диалоги также архивируются на вашей странице, поэтому в случае необходимости вы можете перечитать их для поиска подсказок по учебе. Если вы считаете какую-то подсказку полезной или вам просто понравился другой пользователь, то вы можете наградить его специальными очками, которые будут показаны в его профиле. Возраст пользователей и их фамилии не отображаются.
Grockit использует модель подписки и сейчас насчитывает сотни тысяч зарегистрированных пользователей. Главный директор Grockit Рой Гилберт сказал, что Grockit растет на одну среднюю американскую высшую школу в день и продолжит агрессивно расти на протяжении лета 2014 г. Grockit также расширяется в направлении сервисов для подготовки студентов к широкому кругу различных стандартных тестов и в направлении сотрудничества с такими организациями, как
KIPP (knowledge is power program) Academy, которые помогают студентам из бедных семей поступать в колледж.
К 2016 г., по мнению Гилберта, Grockit должен стать наиболее эффективным ресурсом для каждого человека, которому предстоит подготовка к стандартному тесту. Если Grockit достигнет этой цели, то он добьется успеха и расположения у множества клиентов, сотрудников и инвесторов.
-
2.1. Данные Grockit
Данные соревнования Grockit содержат 4851475 тренировочных записей и 93100 тестовых результатов, которые нужно предсказать, количество студентов I =179106, количество задач J =6046. Следовательно, известные данные составляют около 0.45% теоретической полной информации. Структура данных очень простая: мы имеем три столбца: индекс студента, индекс задачи и результат (1 в случае верного решения и 0 иначе).
-
2.2. Эксперименты
Рис. 1 показывает сходимость алгоритма как функции индекса глобального цикла. Вертикальная ось показывает величину функции потерь L ( A , B ,0,0), где 500000 наблюдений были случайно удалены из тренировочной выборки и использовались для тестирования (проводилось 30 испытаний со случайными разбиениями).
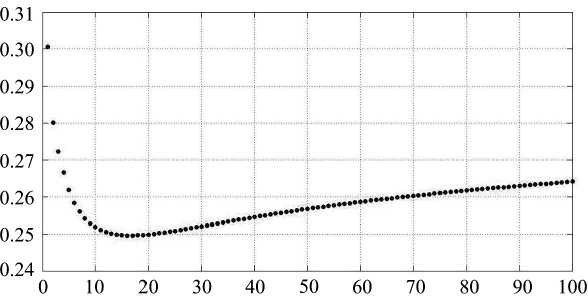
Рис. 1. Сходимость алгоритма LF+SGD: L(A,B,0,0) как функция глобальной итера- ции (относительно горизонтальной оси)
Для этих экспериментов использовались следующие параметры: K = 5, λ 1 = 0.022, λ 2 = 0.016, µ 1 = 0.006, µ 2 = 0.0085 .
Замечание 3. Приведённые выше значения регулирующих параметров µd , d = 1,2
использовались только для тренировки. Скользящий контроль проводился по формуле (3) без регулирования, т.е. µd = 0, d = 1,2 .
В базе данных имеются 54.74% правильных ответов или меток. В дополнение мы сгенерировали случайным образом вторичный вектор целевой функции с аналогичной пропорцией корректных ответов.
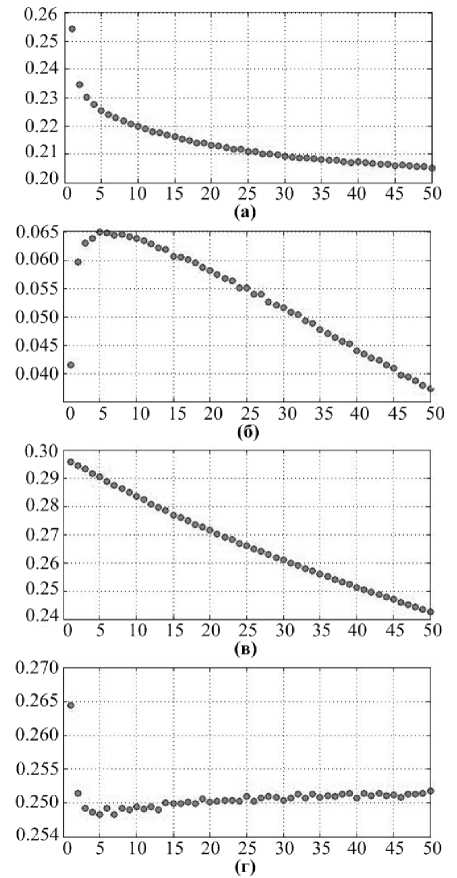
Рис. 2а и 2в показывают сходимость алгоритма в случае оригинальных и случайных меток. Можно видеть, что ошибка в случае оригинальных меток сначала очень быстро уменьшается, а затем процесс убывания замедляется. По-видимому, поведение функции потерь в течение начального периода следует объяснить некоторыми скрытыми зависимостями, содержащимися в данных. Алгоритм обнаруживает эти зависимости очень быстро. В случае случайных меток ошибка уменьшается достаточно гладко и может быть объяснена переобучением: на каждом шаге к модели добавляется I+J новых параметров. Рис. 2б наиболее интересен: он показывает разницу между графиками на рис. 2в и 2а. Эта разница увеличивается до некоторого максимального значения, а затем уменьшается. Можно предположить, что это максимальное значение (на горизонтальной оси) может быть использовано в качестве критерия для выбора количества факторов K . Эта гипотеза подтверждается графиком на рис. 2г. В соответствии с рис. 2б и 2д можно сказать, что оптимальное количество факторов K =5.
Тепловая карта (hot-map), представленная на рис. 3, показывает поведение ошибки скользящего контроля в зависимости от набора параметров: а – λ 1 по вертикали, µ 1 по горизонтали; б – λ 1 , λ 2 ; в – µ 1 , µ 2 ; г – λ 2 , µ 2 . Рис. 3в иллюстрирует значимость регуляризации для преодоления проблемы переобучения. При проведении экспериментов использовались значения K = 5 и N = 24 .
Замечание 4. Рис. 3 показывает результаты скользящего контроля ниже 0.249 в случае, когда параметры выбраны правильно. Этот результат представляется весьма конкурентоспособным с учетом результатов, показанных другими участниками.
-
3. Соревнования по анализу данных Chess 2010 и Chess 2011
0.20
0.065
0.060
0.055
0.050 -
0.045
0.040
0.26 0.25 0.24
0.23 0.22 0.21
0.30
0.29
0.28
0.27
0.26 -
0.25
0.24
Система рейтингов Эло была разработана венгерским физиком Арпадом Эло в 1950-х гг. и адаптирована Всемирной шахматной федерацией (ФИДЕ) в 1970 г. На протяжении более сорока лет система Эло служила первичным критерием во всем мире для оценки силы шахматных игроков. Рейтинг ФИДЕ используется при отборе игроков для участия в шахматных турнирах, включая циклы чемпионатов мира и присуждения таких титулов как мастер международного класса и гроссмейстер. Фактически рейтинг Эло стал настолько популярен, что был использован во многих других областях, где требуется сравнительный анализ силы игроков. Однако, несмотря на популярность системы Эло, никогда не было показано, что подход Эло превосходит другие подходы по каким-либо техническим параметрам.
0 5 10 15 20 25 30 35 40 45 50
(а)
О 5 10 15 20 25 30 35 40 45 50
(б)
15 20 25 30 35 40 45 50
(г)
0.2701-----:------
0.265 ■......
0.260 .......: J
0.255 -.......:........
0.250 -Л^.^
0.2541•
О 5 10
О 5 10 15 20 25 30 35 40 45 50
Рис. 2 . Выбор количества факторов K (по горизонтальной оси): а и в – тренировочная ошибка в случае исходных и случайных меток; б – разница между в и а; г – ошибка скользящего контроля, соответствующая а с оптимальным выбором K=5
Существует несколько альтернатив подходу Эло. Например, профессор Марк Гликман разработал системы Глико и Глико-2, которые расширяют систему Эло введением дополнительных параметров, которые отражают стабильность рейтинга игрока. Джеф Сонас (организатор обоих соревнований) разработал Chessmetrics для оптимизации качества прогноза. Отметим также работы [9], [10] и [11], в которых представлено несколько других подходов.
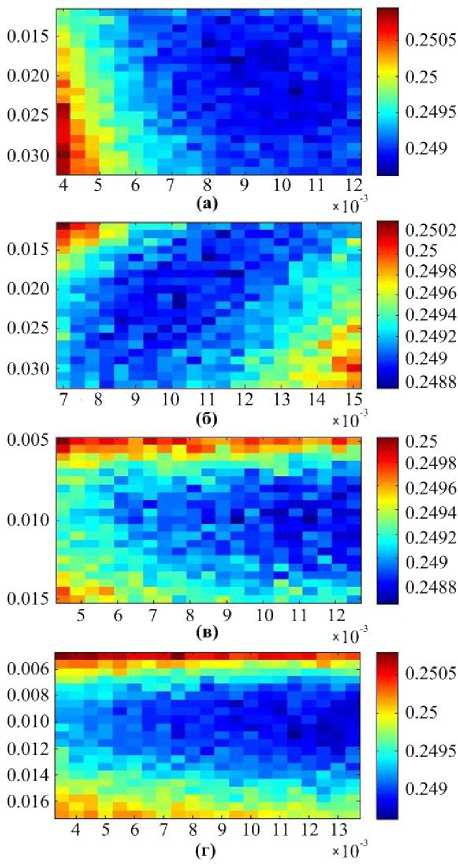
Рис. 3. Выбор регуляризационных и обу- чающих параметров
Большая часть замечаний к системе Эло является отражением её простоты: она идеально подходит в ситуациях, когда вычисление рейтинга является важной частью соревнования, даже если список участников состоит из нескольких сотен игроков. Формула Эло была обоснована теоретически во времена, когда отсутствовали мощности современных вычислительных машин. Появление современных компьютеров и больших баз данных стимулировало развитие методов и подходов, предсказательная сила которых применительно к шахматам значительно превосходит систему Эло. Такие исследования могут иметь значительное влияние на теорию и практику методологии оценивания как в шахматах, так и во всех остальных областях знаний.
Основной целью двух соревнований Chess 2010 и Chess 2011 было выявление перспективных методов для вычисления рейтинга r шахматных игроков. Разработанные нами методы и алгоритмы показали следующие результаты в ходе соревнований: 10-й результат из 252 в 2010 г. и 4-й из 181 в 2011 г. Метод победителя в соревновании Chess 2010, основанный на методе стохастического градиентного спуска, представлен в работе [5]. Продолжительность соревнования в 2010 г. составила 106 дней, а в 2011 г. – 86 дней.
Набор данных для Chess 2011 включал реальные исторические данные, предоставленные Международной шахматной федерацией ФИДЕ. Участники использовали для тренировки своих рейтинговых систем наборы данных из 2327683 результатов игр с участием 85250 шахматных игроков за 11 последних лет. Затем участники использовали свои методики оценивания для предсказания исходов будущих 427361 игр, которые состоялись в следующие три месяца.
-
3.1 Алгоритм вычисления шахматного рейтинга с помощью стохастического градиентного спуска (CR+SGD)
Алгоритм, представленный ниже, имеет несколько отличий по сравнению с соответствующей версией из работы [5]. Во-первых, рассматривается биномиальное отклонение, а не квадратичная ошибка. Во-вторых, представлены все детали относительно очень существенного дополнения о среднем рейтинге соседа (см. формулу (11)). Кроме того, все константы и параметры были вычислены заново с использованием специальной оптимизационной программы на языке C.
В соответствии с моделью Бредли – Терри прогноз вероятности, что игрок i (белые) победит игрока j (черные) составляет
p ij =
1 + e exp( rj - nV
(номер месяца) понимается неуникальное значенИе 1 < t min < t j < t m a x < 132.
Замечание 5. Заметим, что действительные значения регулирующих параметров α и μ не являются существенными (поскольку они обобщаются параметрами β) в (9), (10) и (11), которые определяют структуру формул (14а) и (14б).
В соответствии с формулами (8) и (10) верны следующие соотношения:
где глобальный параметр 0 < в < 1 отражает меньшие шансы на победу черных (все параметры β представлены в таблице).
d S ij
ˆ
dri Plj dSj
= Ру d rj
—
—
p ij ,
p ˆ ij .
(13а)
(13б)
Регулирующие параметры для алгоритма CR+SGD
|
β 1 |
0.8848 |
|
β 2 |
0.7626 |
|
β 3 |
0.1488 |
|
β 4 |
90.0000 |
|
β 5 |
4.0438 |
|
β 6 |
1.5663 |
|
β 7 |
2.0317 |
Целевая функция состоит в минимизации биномиального отклонения с квадратичной регуляризацией
α
L = 3 + ^,3 = — s , ij
# T ( i , j) e T
(а) Обучение
где
s j = P j ln( P ij ) — (1 — P j ) ln(1 — p у ) ,
(б) Тестирование
^ = p X ( r i — q i )2 i e I
, q i =
wj =
[
V max
X wjrj j e Ni
X wj j eNi
, (11)
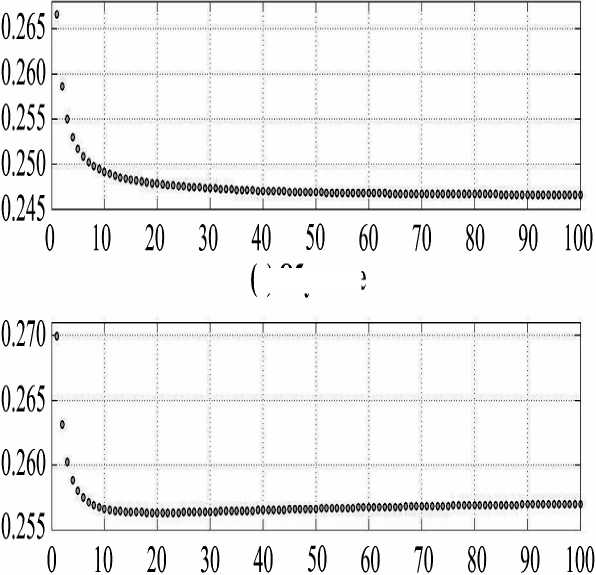
Рис. 4. Сходимость алгоритма CR+SGD как функции от глобальных итераций: а обучение – монотонно убывает; б тестирование – убывает до точки K=21, а затем растет
— t min
—
t min J
β 2
,
где a > 0 и p > 0 - регулирующие параметры, Ni – список соседей или список тех игроков, которые играли с игроком i . Этот список включает: 1) результат; 2) цвет фигур; 3) месяц. Отметим, что каждой паре игроков может соответствовать несколько игр. Следовательно, для упрощения обозначений под tij
Используя формулы (13а) и (13б), можно получить главные формулы для обновления значений:
r,^ r —
— вз AdwjCPj — pij) + в 6
r i — q i ^ , (14а)
S i + 0 7 J
r j ^ r j -
— в3 Лк I — wij (pij — pij ) + в6
r i — q i ^ , (146) s i + в 7 J
где si – количество игр, сыгранных i-м игро- ком за период в 132 месяца, k – индекс гло- бальной итерации, Ak =
1 + в 4
β 5
I k + в 4 J
Рис. 4 иллюстрирует сходимость алгоритма CR+SGD. Как и следовало ожидать, ошибка обучения (а) монотонно убывает. Ошибка тестирования (б) убывает до значения n =21. Отметим сходство между графиками, приведенными на рис. 1 и 4б.
Замечание 6. Центроиды qi являются важными элементами алгоритма CR+SGD, они должны быть пересчитаны с обновлёнными рейтингами после каждой глобальной итерации.
Замечание 7. Используя описанный выше алгоритм CR+SGD, можно вычислить рейтинги шахматных игроков в соответствии с информацией, имеющейся за предыдущие 130, 131 и 132 месяца. Эти рейтинги будут различными и могут быть использованы для вычисления вторичных признаков, таких как первые и вторые производные. В комбинации с некоторыми вторичными признаками мы можем сформировать базу данных для R, а затем использовать такие функции, как GBM или randomForest для вычисления требуемых вероятностей для результатов игр.
Заключительные замечания и выводы
Фактически предложенные алгоритмы LF+SGD и CR+SGD представляют гибкие и простые структуры, которые можно применить и тестировать с разными регулирующими параметрами. Алгоритмы реализованы на языке C и работают очень быстро. Как следствие, можно провести много тестов в целях оптимизации регулирующих параметров. В случае LF+SGD выяснено, что использование двух различных параметров обучения приводит к улучшению качества факторных разложений.
Логично предположить, что начальные значения параметров обучения являются достаточно большими. Затем они должны быть уменьшены, что является предметом дальнейших исследований. Регуляризация представляет собой необходимую и очень важную часть систем на основе SGD. Число факторов не должно быть очень большим, чтобы предотвратить переобучение. С другой стороны, малое число факторов приводит к потере важной информации. В работе представлен непараметрический критерий для выбора параметра K – число факторов. Структура SGD является идеальным подходом для обработки больших списков данных (в случае разреженных матриц).
Эффективность представленного метода была подтверждена в ходе трёх международных соревнований по анализу данных на платформе Kaggle. Дальнейшие улучшения могут быть достигнуты с применением однородного ансамблирования (при использовании так называемых паспортов скользящего контроля), которое рассмотрено в работе [13].
Список литературы Два алгоритма на основе техники стохастического градиентного спуска для рекомендательных систем
- Oja E., Ilin A., Luttinen J., Yang Z. Linear expansions with nonlinear cost functions: modelling, representation, and partitioning//Plenary and Invited Lectures, WCCI 2010, Edited by Joan Aranda and Sebastia Xambo. Barcelona, Spain, 2010. P. 105-123.
- Lee D., Seung H. Learning the parts of objects by nonnegative matrix factorization//Nature 401. 1999. P.788-791.
- Nikulin V., McLachlan G.J. Classification of imbalanced marketing data with balanced random sets//JMLR: Workshop and Conference Proceedings. 2009. Vol. 7. P. 89-100.
- Nikulin V., Huang T.H. Unsupervised dimensionality reduction via gradient-based matrix factorization with two learning rates and their automatic updates//Journal of Machine Learning Research, Workshop and Conference Proceedings. 2012. Vol. 27. P. 181-195.
- Sismanis Y. How I won the Chess ratings -Elo vs the Rest of the World Competition//arXiv:1012.4571v1. 2010.
- Takacs G., Pilaszy I., Nemeth B., Tikk D. On the Gravity Recommendation System//KDD Cup Workshop at SIGKDD 2007 San Jose, California, USA. 2007. Vol. 7. P. 22-30.
- Rendle S. Factorization Machines with libFM//ACM Transactions on Intelligent Systems and Technology 3. 2012. P. 1-22.
- Glickman M.E. Parameter estimation in large dynamic paired comparison experiments//Appl. Statist. 1999. Vol. 48(3) P. 377-394.
- Furnkranz J., Hullermeier E., Cheng W., Park S.H. Preference-based reinforcement learning: a formal framework and a policy iteration algorithm//Machine Learning. 2012. Vol. 89(1).P. 123-156.
- Sun Q., Pfahringer B. Pairwise meta-rules for better meta-learning-based algorithm ranking//Machine Learning. 2013. Vol. 93(1) P. 141161.
- Dangauthier P., Herbrich R., Minka T., Gra-epel T. TrueSkill Through Time: Revisiting the History of Chess//NIPS. 2007.
- Huang T.K., Weng R., Lin C.J. Generalized Bradley-Terry Models and Multi-Class Probability Estimates//Journal of Machine Learn ing Research. 2006. Vol. 7. С. 85-115.
- Nikulin V., Bakharia A., Huang T.H.: On the evaluation of the homogeneous ensembles with CV-passports//PAKDD 2013, LNCS Springer, J. Li et.al. (Eds.). 2013. Vol. 7867. P. 181-195.


