Двумерное математическое моделирование изоэлектрического фокусирования средствами интегрированной среды разработки FreeFem++
Автор: Сахарова Людмила Викторовна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 5 (56) т.11, 2011 года.
Бесплатный доступ
Решена задача о 2D-распределении биополимеров при изоэлектрическом фокусировании в прямоугольной электрофоретической камере в иммобилизованном градиенте pH. Программное обеспечение, созданное на языке FreeFem++, позволяет в наглядной форме исследовать картину изоэлектрического фокусирования во времени, а также моделировать и оптимизировать реальный эксперимент.
Изоэлектрическое фокусирование, математическое моделирование, метод конечных элементов, интегрированная среда разработки
Короткий адрес: https://sciup.org/14249597
IDR: 14249597 | УДК: 004.942
Текст научной статьи Двумерное математическое моделирование изоэлектрического фокусирования средствами интегрированной среды разработки FreeFem++
Введение. Изоэлектрическое фокусирование (ИЭФ) является одним из наиболее эффективных электрохимических методов, применяемых для идентификации компонентов и фракционирования многокомпонентных биохимических смесей. Этот метод широко используется в биохимии, различных отраслях медицины, генетике, фармакологии, пищевой промышленности.
Основной задачей математического моделирования ИЭФ является создание моделей, позволяющих повысить разрешающую способность метода, оптимизировать эксперимент в целях экономии материальных и временных затрат. Для этого необходимы наглядные модели, позволяющие исследовать процесс ИЭФ во времени, а также установить взаимосвязь между динамикой процесса и параметрами электрофоретической камеры (ЭК).
На решение перечисленных задач направлены наши исследования. Полученная модель основана на классических математических моделях [1, 2] и содержит новый подход к их решению в интегрированной среде разработки FreeFem++ [3].
Язык программирования FreeFem++ выбран как оптимальный для решения указанной задачи по ряду причин. Во-первых, FreeFem++ изначально предназначен для численного решения дифференциальных уравнений в частных производных методом конечных элементов в 2D-пространственном случае. Во-вторых, по сравнению с коммерческими пакетами, предназначенными для решения уравнений в частных производных, FreeFem++ обладает уникальной возможностью доступа ко всем внутренним данным и возможностью создания собственных алгоритмов. В-третьих, в настоящее время существует развитая теория решения задач математической физики средствами языка FreeFem++, в частности, разработан обширный математический аппарат для решения задач электрофореза как метода разделения многокомпонентных смесей на отдельные компоненты при помощи внешнего электрического поля [4]. В-четвертых, язык FreeFem++ относительно прост в использовании, поскольку запись алгоритмов на нем близка к C++, а эффективность кода по скорости близка к оптимальной. Наконец, в-пятых, язык FreeFem++ обладает развитым интерфейсом, имеет собственный «визуализатор», поддерживающий рисование сетки, изолиний конечно-элементарных линий и векторных полей.
Применение языка FreeFem++ в рассматриваемом случае позволило создать программное обеспечение, моделирующее поведение сложных систем биополимеров в заданных условиях ИЭФ. Физическая постановка задачи. В электрофоретическую камеру, имеющую форму прямоугольника длиной l и высотой h , помещена смесь N биополимеров в виде пятна заданной конфигурации. В ЭК задан фиксированный градиент pH .
Для каждого из биополимеров известны его константы диссоциации pKk), pK2k), а также коэффициенты миграции цk. Известно также количество биополимеров Dk, помещенных в ЭК. Предполагается, что температура внутри ЭК постоянна и равна T.
Требуется исследовать динамику концентрации каждого из N биополимеров во времени под действием электрического поля: рассчитать неизвестную концентрацию биополимеров У k = У k ( x , у , t ) , k = 1,2,..., N и визуализировать результаты расчетов с помощью линий уровня. Математическая постановка задачи. Предполагается, что диссоциация биополимера под номером k описывается уравнениями:
NH + RCOOH о NH 2 RCOOH+H + , NH 2 RCOOH о NH 2 RCOO - +H+ .
Молярные концентрации NH + RCOOH , NH 2 RCOO - , NH 2 RCOOH - положительного, отрицательного и «нейтрального» ионов биополимера - обозначим y k , y- , y k . Аналитическая концентрация биополимера определяется формулой: y k = y k i; f i; - 1 . В равновесном состоянии концентрации ионов связаны с аналитической концентрацией следующими соотношениями:
a =ak Ук, У-1 = a -Л k, Ук = (1 -ak -a-1Х к, к H2 к K ( k) K кk)
k d k 2
-
1 ^( k)К(k )+^( k )Я + Я2 , 2 Я( k)К(k )+Я( k )Я + Я2 ,
-
11. i j. X. 2 х.1 11 11,1 1 х. 1 1 х. 2 i^-1
где a k и a k - степень диссоциации биополимера; Н - концентрация ионов водорода.
В условиях иммобилизованного (фиксированного) градиента pH (т.е. функции Н = Н ( x , у ) , заданной в области D = { x е [0; l ], у е [0; h ]} и неизменной во времени) концентрации биополимеров описываются краевой задачей:
Dk =еЦk , где е = RT/ F .
Уравнение (1) есть уравнение массопереноса, полученное на основании уравнения потока биополимера и основного уравнения теории переноса. Уравнения (2), (3) выражают закон Ома, записанный в предположении, что электрический ток в растворе создается миграцией биополимеров, а также ионов водорода. Краевое условие (4) отражает факт, что граница ЭК непроницаема для электролита и, следовательно, поток каждого из биополимеров через границу равен нулю. Краевые условия (5) соответствуют предположению о том, что верхняя и нижняя границы области изолированы, а значит, электрический ток через них равен нулю. Условия (6) означают, что для ЭК определена разность потенциала между ее левой и правой границами. Наконец, интегральное условие (7) отражает тот факт, что масса каждого биополимера в течение всего эксперимента остается неизменной и равной Mk .
Следует учесть, что при интегрировании представленной интегродифференциальной краевой задачи требуется также использовать распределение в начальный момент времени ^kк = ^ k ( x , у ,0 ) в некоторой заданной ограниченной области.
Система уравнений (1)-(7) представляет собой серьезную проблему для численного решения, в первую очередь, из-за наличия интегрального условия (7). Решение ее классическими конечно-разностными методами требует предварительных преобразований системы, составления сложного алгоритма, значительного объема вычислений.
В то же время, применение интегрированной среды разработки FreeFem++ к решению задачи позволяет минимизировать как предварительные преобразования, так и непосредственную вычислительную работу.
Численная реализация задачи на FreeFem++. Алгоритм решения рассматриваемой задачи на языке FreeFem++ включал в себя шесть основных этапов. Рассмотрим кратко каждый из них.
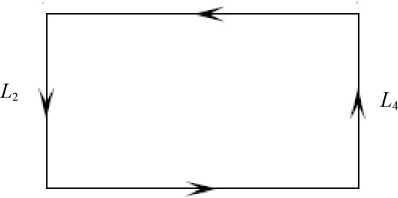
Параметризация границ области интегрирования. В соответствии со стандартами FreeFem++, граница области была обозначена через Г (замкнутый прямоугольный контур, обходимый против часовой стрелки); при этом нижнюю и верхнюю границы области обозначали L 1 ( у = 0 ) и L 3 ( у = h ) ; правую и левую соответственно L 2 ( x = l ) и L 4 ( x = 0 ) (рис.1).
(0, Л) L3 (I, ^
(0,0) (/, 0)
Рис.1. Область интегрирования D = {( x , у ):[0, l ]х[0, h ]}
Аппроксимация временных производных. В соответствии с требованиями языка FreeFem++ задача была приведена к слабой (вариационной) формулировке. Однако непосредственное (без составления алгоритма) решение возможно только для линейных стационарных задач. Поскольку рассматриваемая задача моделирования ИЭФ достаточно сложна, потребовалось пошаговое решение, позволяющее свести исходную задачу к набору линейных краевых задач.
Поиск решения задачи (1)-(7) осуществляли на интервале времени [ 0, T ] . Был задан набор значений t m = m т , где т - шаг по времени, а также введены обозначения:
^ m ( x, У W к ( x, У, t m ) , t m = m Т .
С учетом аппроксимации производной по времени конечной разностью задача (1)-(7) была преобразована к виду:
к m + 1
^ к
—
т
m
— div ( D f • V^ f* + 1 + Ц к ^ m + 1 ( a f — a — 1 ) Vф m ) = 0 ,
к = 1,2,
...
, N
a f =
( H m + 1 ) 2
2 , K к ) k 2 к ) + k < к ) H m + 1 + ( H m + 1 )
a 2 =
K 1 ( k ) K 2 ( k )
,
K 1 к ) K 2 к ) + K < к ) H m + 1 + ( H m + 1 )
- m Аф m + Vф m V- m = 0 ,
N
- m = £ ц к ( a f +a 2 ) ^ m + Ц H H , к = 1
f m+m +1 _
D f -|^- + Ц к ^ mm + 1 n ( a f — a—1 ) Vф m
< d n
= 0, аd
: 1
< д n J
= 0, y=0
: 1
< д n J
= 0 , y = h
ф m L=. =ф„
ф x = l = ф 2 ,
jj ^ m + 1 ( X , y ) dxdy = M f .
D
Таким образом, если £ m ( x , y ) = £ к ( x , y , tm ) и ф m ( x , y ) = ф ( x , y , tm ) известны, то для определения функции £ m + 1 ( x , y ) = £ к ( x , y , tm + 1 ) имеет место стационарная краевая задача (8)-(15).
Решая ее для m = 0,1,
...
, n , можно получить приближенное решение нестационарной задачи. Для
решения задачи используется неявная аппроксимация, т.е. все члены уравнений, не содержащие производной по времени, выбираются в точке t m + 1 = ( m + 1 ) т , а аппроксимация производной по времени осуществляется в точке t m = m т .
Переход к слабой (вариационной) формулировке задачи. В основе метода конечных элементов лежит приведение задачи к слабой (вариационной) формулировке.
Первоначально был осуществлен переход к слабой формулировке уравнения (10). Для этого использовали исходное уравнение, приводящее к уравнению (10):
div ( - m Vф m ) = 0 .
Умножение исходного уравнения на пробную (тестовую) функцию 0 , интегрирование по области
D с последующим интегрированием по частям привело к уравнению:
jj - m Vф m V0 dxdy + cf 0- m дФ ds = 0 .
D Г d n
В соответствии с краевыми условиями (13)
j 0- m дф ds = 0 ,
-
L 1 1 L 3 d n
а значит,
jj-
D
m
^ 5ф m d0 дф m d0 < д X д X д y д y
dxdy + j 0- m ^=- ds = 0 .
L 2 1 L 4 д n
Из краевых условий (14) следует, что ф"I = ф,, ф|L =ф2. (17)
I L 4 2
В языке FreeFem++ имеется большой набор быстрых алгоритмов для решения задач, приведенных к слабой формулировке. В данном случае для решения задачи (16), (17) был выбран стандартный код с привлечением LU-алгоритма:
problem pbPhi(phi, v, solver = LU) = int 2d(Th)(sigma * (dx(phi) * dx(v) + dy(phi) * dy(v)))
+on ( L 4 , phi = phil) + on ( L 2 , phi = phi 2).
Аналогично была получена слабая формулировка уравнений (8). Умножение каждого из уравнений (8) на пробную (тестовую) функцию 6k и интегрирование по частям в области D при- вело к уравнению:
JJ 6 k div ( D k VS m + 1 + И k 5 m + 1 ( a k - a - , ) Vф m ) =
D
= JJ V6 k ( D k VS " + 1 + И k 5 m + 1 ( a k - a - , ) Vф " dxdy + D
Г ^£ m + 1
—
к x дф m L a k ,)—— ds .
— 1 d n J
+^6k Dk - + Иk5m+1(ak г у О n
В силу краевого условия (12) криволинейный интеграл в правой части последнего уравне- ния равен нулю, а значит, уравнение принимает вид:
у m + 1 £ m
JJ 6k ' k + DkV6k\5m+1 + Иk5m+1 (ak — a—1)V6kVфm dxdy = 0 .
D L T
В соответствии с требованиями языка полученные уравнения необходимо просуммировать по всем k , в результате чего получим слабую формулировку задачи, состоящей из уравнений (8), (12):
N
XJJ
Гд ^ m + 1
-k s^ + D t
k = 1 D V
т
fdT ,_ de, 11
V Вx Вx Вy Вy Jy
dxdy +
+jjf И k 5 m + 1 ( a k — a — 1 ) ' ф ' + ' ф ' 11 dxdy — JJ 6 k dxdy = 0 . (18)
JD у yd x В x В y В y J J D т
Для решения задачи (18) также был выбран код с использованием LU-алгоритма (для простоты рассмотрен случай N = 2):
problem pb 4 c ( c 1 , c 2 , v 1 , v 2 , init = m, solver = LU )
= int 2 d ( Th )( c 1 * v 1 /dt + epsilon1 * ( dx ( c 1) * dx ( v 1) + dy ( c 1) * dy ( v 1)))
+ int 2 d ( Th )( mu 1 * ff * c 1 * ( dx(phi ) * dx ( v 1) + dy(phi ) * dy ( v 1))) - int 2 d ( Th )( cold 1 /dt * v 1)
+ int 2 d ( Th )( c 2 * v 2 /dt + epsilon 2 * ( dx ( c 2) * dx ( v 2) + dy ( c 2) * dy ( v 2)))\ + int 2 d ( Th )( mu 2 * ff* c 2 * ( dx (phi ) * dx ( v 2) + dy (phi ) * dy ( v 2))) - int 2 d (Th )( cold 2 /dt*v 2);
Стандартные действия. Для параметризации границ области был использован следующий код:
x 1 = 0 ; y1 = 0 ; x 2 = w 1 ; y 2 = 0 ; x 3 = w 1 ; y 3 = h 1 ; x 4 = 0 ; y 4 = h 1;
border L 1( t = 0 , 1){ x = (1 -t ) * x 1 + t*x 2 ; y = (1 -t ) *y 1 + t*y 2 ; };
border L 2( t = 0 , 1){ x = (1 -t ) *x 2 + t*x 3 ; y = (1 -t ) *y 2 + t*y 3; };
border L 3( t = 0 , 1){ x = (1 -t ) *x 3 + t*x 4 ; y = (1 -t ) *y 3 + t*y 4; };
border L 4( t = 0 , 1){ x = (1 -t ) * x 4 + t *x 1 ; y = (1 -t ) * y 4 + t* y 1; };
Триангуляция области (т.е. замена ее конечным набором треугольников) осуществлялась посредством оператора mesh Th = buildmesh(L1(10 * n) + L2(5 * n) + L3(10 * n) + L4(5 * n))
и приводила к генерированию сетки (рис.2).
Рис.2. Сетка интегрирования
В качестве конечных элементов были выбраны кусочно-квадратичные непрерывные конечные элементы Vh ( Th,P 2) , обеспечивающие одновременно высокую точность и скорость решения.
Организация цикла движения по времени. Особого внимания при создании программного обеспечения потребовало создание цикла движения по времени. Цикл был организован с помощью стандартного оператора for ( m = 0; m< 1000; m + + ), на каждом шаге которого требовалось обеспечивать условие нормировки.
При решении задачи необходимо было иметь в виду, что по физическому смыслу концентрация биополимера есть величина неотрицательная. Одним из приемов, который можно использовать для сохранения неотрицательности, является обработка на каждом временном шаге дискретного набора концентраций в узлах сетки. Если шаг расчета достаточно мал и при вычислении решения в каких-либо узлах появляются отрицательные значения концентраций, то их можно принять равными нулю.
Пусть на некотором временном шаге tm существует решение, которое обозначим 2 ( x , y , t m ) . Определим отклонение среднего значения вычисленной концентрации от действительного значения по формуле:
me-D jj ^ (x, y, tm)—Mk dxdy=^, где Mk - масса k-го биополимера; mesD - мера области D.
Концентрацию на ( m + 1 ) -м шаге вычисляем по формуле:
^ k ( x , у , t m + 1 ) = ^ k ( x , y , t m M k .
Очевидно, что в этом случае масса будет сохраняться автоматически:
JJ ^ m + 1 ( x , y ) dxdy = M k , k = 1, ... , N ,
D что соответствует условию нормировки (15).
Перерасчет концентрации осуществлялся с помощью следующих кодов:
for (int j = 0; j < c 1[] .n ; j + + ){if ( c 1[][ j '] < 0) c 1[][ j '] = 0;
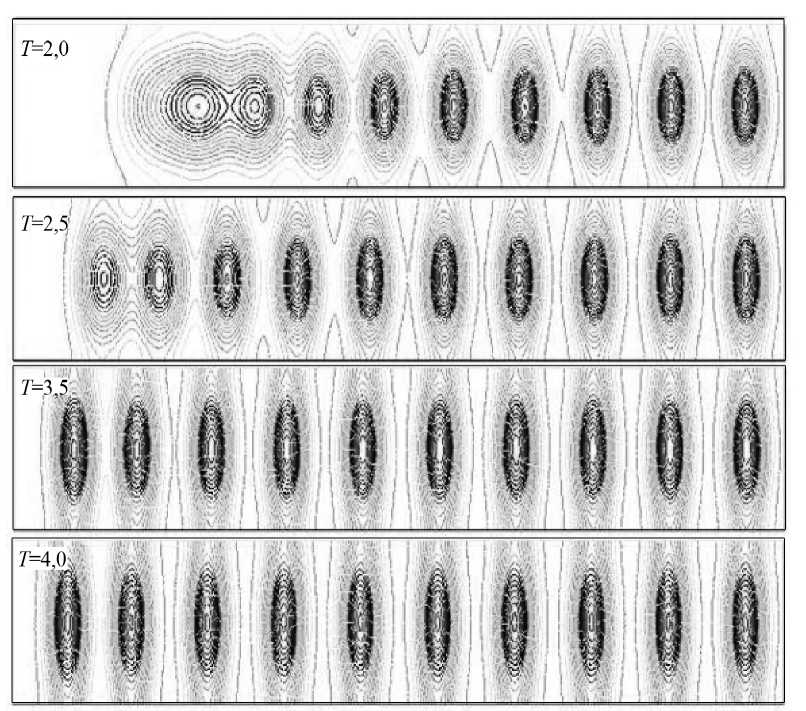
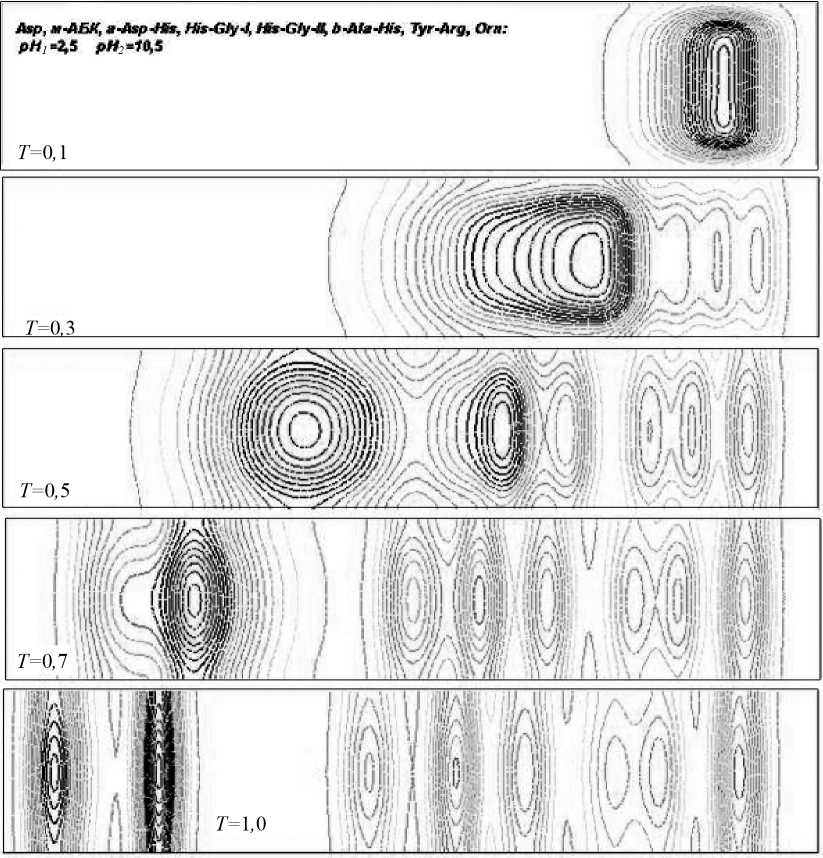
for (int j = 0; j real averC2 = (int 2d(Th)(c2) - massac2)/area0; c2 = c2 - averC2; Визуализация расчетов. Визуализация расчетов на каждом шаге по времени обеспечивалась кодом программы plot(sigma, cmm = +t), выводившим на экран линии уровня функции ст, в полной мере отражающей распределение концентраций биополимеров. Особое внимание было уделено вопросу о задании начального распределения концентраций биополимеров, т.е. формы, размеров и расположения в ЭК пятна смеси разделяемых веществ. Начальное распределение полимеров задавали либо в виде круга [5]: ^k (x,У) = Ak (1 + th(-P((x — x0 )2 +(У-У0)2 -r02))) , (Ak - амплитуда, p - параметр сглаживания, (x0,y0) - центр пятна, r0- его радиус), либо в виде прямоугольника со сглаженными углами: ^k (x, У ) = 0, 25Ak [th (Р1 (x — x2 )) — th (Р1 (x — x1 ))][th(р2 (У — У2 )) — th (р2 (У — У1 ))], (Р1, в2 - параметры сглаживания углов прямоугольника, занимающего область {(x,у):x1 < x< x2,У1 < у< у2}). Исследование динамики концентраций биополимеров. Пример 1 (рис.3). Расчеты проводили для десяти гипотетических аминокислот с равномерным распределением изоэлектрических точек: ApI = 0,3, ApK = 0,15 . При этом предполагалось, что иммобилизованный градиент задан линейной функцией. а) Рис.3. Процесс ИЭФ десяти аминокислот с равномерным распределением изоточек: ApI = 0,3 , ApK = 0,15 ; градиент pH линейный, pHn = 7,0 , pHk = 10,0 (начало): а – первый этап; б – второй этап б) Рис.3. Окончание Из рис.3 видно, как осуществляется процесс расслоения исходной смеси на фазы. Исходная круговая форма пятна со временем трансформируется в эллиптическую, а затем фракция приобретает вид вертикальной полосы. По окончании расслоения процесс приобретает стационарный характер, так как для T = 3,5 и T = 4,0 формы пятен имеют минимальные различия. Численный эксперимент показал, что на итоговую картину не влияет исходная форма пятна смеси – для распределения в виде прямоугольника наблюдалась картина, аналогичная рис.3. Результаты проведенного исследования подтверждаются результатами одномерного моделирования ИЭФ [6]. Пример 2 (рис.4). Проведены расчеты для восьми стандартных аминокислот Asp , м - АБК , α - Asp - His , His - Gly - I , His - Gly - II , β - Ala - His , Tyr - Arg , Orn . В расчетах были использованы характеристики биополимеров-носителей [7] (см. таблицу). Рис.4. Процесс ИЭФ восьми стандартных аминокислот Asp , м - АБК , α - Asp - His , His - Gly - I , His - Gly - II , β - Ala - His , Tyr - Arg , Orn ; градиент pH – линейный, pHn = 2,5 , pHk = 10,5 Характеристики стандартных аминокислот Аминокислота pK1(k) pK2(k) pI ΔpK Коэффициент подвижности, ×104 Asp 1,88 3,65 2,77 1,77 3,078 м-АБК 3,12 4,74 3,93 1,62 3,119 α - Asp - His 3,02 6,82 4,92 3,80 2,187 His - Gly - I 5,28 7,8 6,80 2,02 2,487 His - Gly - II 6,27 8,57 7,42 2,30 2,487 β - Ala - His 6,83 9,51 8,17 2,68 2,3837 Tyr - Arg 7,55 9,80 8,68 2,25 1,638 Orn 8,65 10,76 9,70 2,11 3,223 Из рис.4 видно, что наиболее четкое разделение наблюдается для аминокислот Asp , м - АБК и α - Asp - His , поскольку шаг по ΔpI для них максимален. В то же время, β - Ala - His и Tyr - Arg выделены преимущественно в виде смеси из-за относительно близких изоэлектрических точек. Таким образом, созданное программное обеспечение позволяет предсказать поведение сложных систем биополимеров в заданных условиях ИЭФ. Выводы. 1. Построена универсальная двумерная математическая модель ИЭФ в прямоугольной электрофоретической камере с фиксированным (иммобилизованным) градиентом pH, описывающая поведение в процессе ИЭФ заданного числа произвольных биополимеров, для которых должны быть известны константы диссоциации pK1( k), pK2(k), а также коэффициенты миграции µk. Кроме того, для работы с моделью необходимо задать градиент pH в ЭК. Математическая модель представляет собой краевую задачу, для решения которой были использованы средства интегрированной среды разработки (языка) FreeFem++. На основе стандартных средств языка созданы собственные алгоритмы решения и программа, визуализирующая результаты расчетов и позволяющая наблюдать за трансформацией пятен биополимеров во времени. Построенная модель позволяет исследовать динамику концентраций биополимеров в зависимости от параметров ЭК – разности потенциалов и градиента pH; параметров самих биополимеров – констант диссоциации, коэффициентов миграции, а также начальной формы пятна смеси. 2. Проведенные расчеты показали, что разделение аминокислот происходит тем лучше, чем меньше значения ΔpK по сравнению с длиной интервала между их изоэлектрическими точками. 3. На основании расчетов можно прогнозировать результат ИЭФ для заданного режима ЭК и системы биополимеров. С помощью модели также можно оптимизировать эксперимент, варьируя состав электролита, разность потенциалов и pH в ЭК. Таким образом, построенная модель может быть использована для оптимизации реального эксперимента, повышения разрешающей способности метода, а также экономии времени и средств.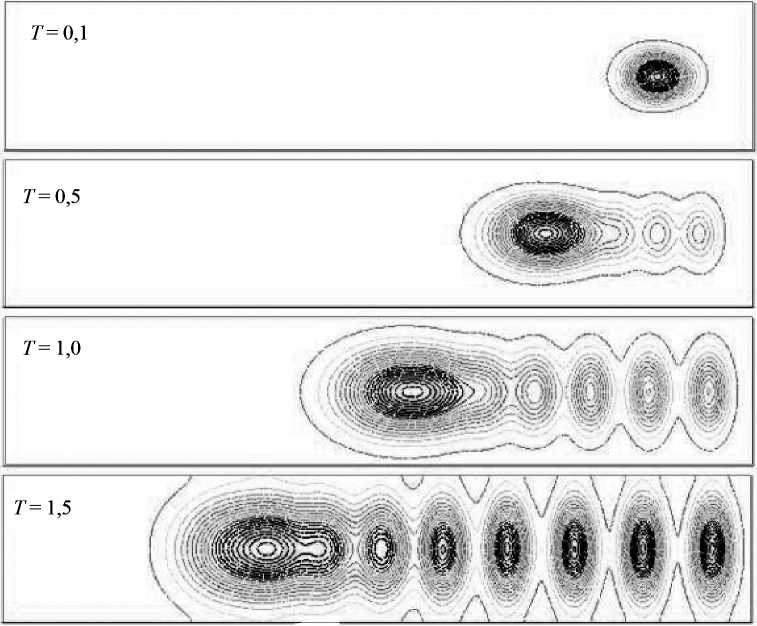
Список литературы Двумерное математическое моделирование изоэлектрического фокусирования средствами интегрированной среды разработки FreeFem++
- Бабский В.Г. Математическая теория электрофореза: применение к методам фракционирования биополимеров/В.Г. Бабский, М.Ю. Жуков, В.И. Юдович. -Киев: Наук. думка, 1983. -202 с.
- Жуков М.Ю. Массоперенос электрическим полем/М.Ю. Жуков. -Ростов н/Д: Изд-во Рост. ун-та, 2005. -216 с.
- Hecht F. FreeFem++. Version 2.17-1 [Electronic resource]/F. Hecht [et al.]. -Mode of access: http://www.freefem.org/ff++.
- Жуков М.Ю. Использование FreeFem++ для решения задач математической физики/М.Ю. Жуков, Е.В. Ширяева. -Ростов н/Д: ЦВВР, 2007.
- Matuzevicius D. Mathematical Models of Oversaturated Protein Spots/D. Matuzevicius, A. Serackis, D. Navakauskas//Electronics and electrical engineering (Medicine technology). -2007. -№1(73).
- Sakharova L.V. Anomalous pH-gradient in Ampholyte Solution/L.V. Sakharova, V.A. Vladimirov, M.Y. Zhukov. -arXiv: 0902.3758vl [physics.chem-ph] 21 Feb 2009.
- Ригетти П. Изоэлектрическое фокусирование. Теория, методы и применение/П. Ригетти. -М.: Мир, 1986. -398 с.


