Кіріспе

Жоғары класты тетіктер (ЖКТ) кинематикасы бойынша талдау көрсеткендей, олардың жағдайларының кинематикалық талдауының әртүрлі графикалық және сандық 9дiстeмeлeрi жасалды [1-4]. ЖКТ кине-матикалық талдаудың аналитикалық әдісі әлі күнге дейын анықталмаған. Осы жұмыста ЖКТ жаFдайларыныц кинематикалык талдау- ына ерекше әдістеме жасалынды [5]. Ол бұл есепті кейбір ЖКТ үшін аналитикалық түрде, ал қалғандары үшін қарапайым есептеу арқылы шығарды. Бұны тіреуді шартты алмастыру (ТША) деп атады.

Зерттеу нысаны мен әдістері

ТША мэн бул баяндамада ЖКТ - алты буынды Стефенсон тeтiгiн кинематикалык схемасында (1,2 суреттер) зeрттeлeдi:

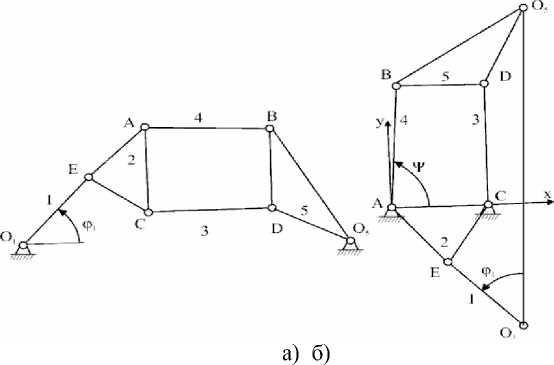
1 сурет - Алты буынды Стефенсон теттн кинематикалык схемасыныц б1р1нш1 тYрi: а) абсолюты KозFалыста, б) салыстырмалы козFалыста

• -    тeтiктiц калыпты тiрeу рeтiндe ЖКМ құрамына кіретін тұйықты қозғалмалы өзгермелі контурдың бір буынын қолдануға болады (1 суретте ол 2 буын);

• -    осы кабылданFан тiрeугe байланысты тeтiк козFалысы карастырылады;

• -    жасалFан калыпты тiрeудiц жэне аралас тұйықты қозғалмалы өзгермелі контурдың бір буынының өзгермелі параметр рeтiндe бурышты алуга болады- ^ бурышы

(1 суретте ол 2 жэне 4  буындардын, арасындаFы бурыш);

• -    тeтiк eндi салыстырмалы козFалысы арқылы қарапайым II класс структураның түрге айналады: I⁽²⁾(4) ---> II⁽²⁾(3,5) ---> II⁽²⁾(1,0 i 0 5 ), ^ = (2)" дeгeнiмiз - ол 2 буын трек деп алынды деген сез);

• -    осы II класс тeтiктiц аналитикалык талдауын жасау кажет;

  _-

  
  

  тетіктің табылған салыстырмалы

  
  

  жағдайы нақты жағдайға айналдырады.

  Осы жұмыста ұсынылған айналмалы жұптармен талдауға арналған әдістерді екінші қатарлы төртінші класты алтыбуынды жазық тетік сүлбелердіңде қалай пайда-лануды көрсетеміз: а) топсалы жұпт ер мен (1 сурет) және б) бір сыртқы ілгерілемелі жұпп ен (2сурет).

  Нәтиже және оның талқылау

  Алты буынды Стефенсон тетігін кинематикалық схемасының бірінші түрін бақылаймыз (1a сурет). O 1 және О 5 бекітпелерінің координанттары берілген O₁-X-Y координаттар жүйесінде; және де ілмек ұзындықтары ^{l O 1 E} , ^l EA , ^l EC , ^l AC , ^l AB , ^l CD , ^l

  BD , ^{BO 5} , ^{DO 5} берілген. Тетігін "бастапқы" орынды есебін аналитикалық жолға қоямыз. A, B, C, E, D топсалардың координаттары жэне бурыш ^ф 1 байланыстырушы ара-қатынастарды табамыз. Шартты түрде бір контурлы буынды, айталық 2 буын, тірек деп алайық. Тетікті A-x-y координат жүйеге қат-ысты қарастырамыз. Тетіктің 2 буыны қатты байланысқан, A-x осі C нүкте арқылы бағыт-талFан. Жиынтьщ координатаны бурыш ^ деп аламыз – ол 2 және 4 буындар бағыттар арасы (1б сурет).

  D нүктесінің орын табамыз, ол үшін _ф ⁽²)

  ^BD бұрышын табамыз, бұл жерде индекс "⁽²⁾" дегеніміз – ол 2 буын тірек деп алынды деген сез (1б-сурет): ^ф™ ^{ф вс + Ф cBD} . B жэне C

  
  

  нүктесінің орналасу  жағдайын табамыз,

  ф (²L_m                  ,.ф (2).

  олүшін ^{ВO 5} бұрышын  анықтаймыз: ^{ВO 5}   =

  
  

  ^ B2D ⁺ ф DB о 5

  
  

  ф В^) = ^arct g

  
  

  y_D

  
  

  —

  
  

  y_В

  
  

  топсаларды

  
  

  анықталады

  
  

  ^BC арқылы қосамыз, ол былай: x^C = l^AC , ^Уc = 0,

  
  

  x B = l AB • cos ^ , У в = l AB • Sin ^

  ^,

  
  

  .^xc ^{— X}D )^{2 + (} У с

  
  

  —

  
  

  2 y_D )²

  ^,

  
  

  ф ВС = arctg

  
  

  У с ^— У в

  
  

  x_r — x_R

  CB

  
  

  .

  
  

  ф (2), = ± arc cos ;

  
  

  табамыз:

  
  

  ^фСВП

  Енді ^CBD бұрышын

  1 2 BC + 1² BD — 1 ² CD

  BC BD)    J

  
  

  ^,

  
  

  ± белгiлерi B-D-C  тобынын,  бYрмелеуiн

  
  

  анықтайды. Онда салыстырмалы

  
  

  B нүктесінің жағдайы қозғалыста:

  
  

  = ± arccos

  
  

  ,

  /² +/²

  ¹ BD ⁺ ^ 0₅

  
  

  ^XD ^{— Х}В

  
  

  , ф DB 0 5

  
  

  —

  
  

  z²

  DO

  
  

  2/

  BD BO

  
  

  - , ± белгiлерi D-

  
  

  B-O₅ тобының бүрмелеуін анықтайды. Онда

  
  

  O 5 нүктесі

  
  

  салыстырмалы

  
  

  қозғалыста:

  
  

  x_D

  
  

  x_B y_B

  
  

  ⁺ l BD

  
  

  •

  
  

  cos( ф B²D ) . sin( ф BD )

  
  

  .

  
  

  O 5

  
  

  ^xO 5

  y_{O 5}

  
  

  x_В

  
  

  y_В

  
  

  ⁺ l BO ₅

  
  

  •

  
  

  орналасу жағдайын

  
  

  бұрышын

  1 ²„ + 1 ²„

  = ± arccos; —--—

  
  

  ^cos ( ф B²D ⁾

  -^cos(l ^ ^BD ) - . E щктесшщ

  ф (2)_E

  табамыз, ол үшін ^CAE

  _Я              ф с!е

  анықтаймыз: ^CAE

  
  

  —

  
  

  CE

  
  

  2/ ■/

  ^{2 l}AC ^lAE

  
  

  - , ± белгiлерi C-A-

  
  

  E тобының бүрмелеуін анықтайды. Онда

  
  

  Eнүктесі x E I

  
  

  салыстырмалы

  
  

  қозғалыста:

  
  

  x_A

  
  

  y_E

  
  

  y_A

  
  

  бекітпелерін ұзындықтар

  
  

  ⁺ l AE •

  
  

  ^cos ( ф CA⁾E )

  .^cos ( ф CA⁾E ) J . _O1

  
  

  қосамыз. Енді

  
  

  ^;о ₅ ^{— х} о , ^{) 2 + ( У} О ₅

  
  

  ' О₅ ^{— Х} Е ^{) 2 + ( У}о₅

  
  
  
  
  
  

  y O ₁ ) ^{2 ,} y E ) ²

  
  

  .

  
  

  және O 5 l O ₁ O ₅ , l EO ₅ табамыз

  
  

  O 1

  
  

  нүктесінің орналасу жағдайын табамыз, ол

  ф о3о                ф о2о = ф о²р + ф ⁽²⁾О

  үшін    ^{O 5 O 1} анықтаймыз:   ^{O 5 O 1     O 5 E    EO 5 O 1} ,

  
  

  ф О 2 Е = ^arctg

  
  

  = ± arccos

  
  

  Уе ^— У О 5

  
  

  x_E — X,

  
  

  ^,

  
  

  ■ О 5 J ф ЕО О 1

  
  

  I² +l²

  ¹EO₅ ^{+ (} O,O₅

  
  

  ^“

  
  

  OE

  
  

  ^'ео₅  ‘о,о₅

  
  

  ± белгілері E-O 5 -O 1 тобының бүрмелеуін анықтайды. О₁ нүктесінің орналасу жағдайын салыстырмалы қозғалыста табамыз:

  
  

  x_{O 1}

  ^yO 1

  
  

  x_{O 5}

  ^yO 5

  
  

  ^{+ 1}О 1 О 5

  
  

  ^sin( ф O ² O ,) ^cos( ф O ² O ,)

  
  

  Енді абсолюттік қозғалысына өтеміз. Cалыстырмалы қозғалыстан абсолют қозға-лысқа өту формуласын қолданамыз. Cалыс- тырмалы және абсолют жүйелерінің арасын-

  
  

(2)      (2)

даFы абцисса осшщ бурышы а = y AC - y ^o болады. Абсолюттік (шынайы) топсалардың координаттарын              анықтаймыз:

J X A = ^{( x} A ^- x o , ^{)cos а} + ( У A ^- y_{O |} ^{)sin а} 1 Y A = ⁽ x A ^- x o , ^{)sin а} + ⁽ y A ^- У ц ^{)cos a} , 'Xb = ( X b - X o_x )cos a + ( У в - У о_х )sin а _ ^Y b = ^{( X} b ^- x o ,^{)sin а + (} У в ^- У о ,^{)cos a} , J X_c = ( x _c - x_o )cos a + ( y_c - y_o )sin а 1 Y = ( x C - x _e )sin а + ( y C - У о )cos a ’ J X d = ( X d - x _Oi )cos a + ( y D - У _О1 )sin а 1 Y d = ( X d - X o , )sin а + ( y D - У о_х )cos а

J ^X E = ^{( X} E ^- x o , ^{)cos а + (} У е ^- У о , ^{)sin а}

1 Y E = ^{( x} E ^{- x} o , ^{)sin а + (} У е ^- У o , ^{)cos а}

Топсалар A(X А , Y А ), B(X В ,Y В ), C(X С , Y С ), E(X Е ,Y Е ), D(X D ,Y D ) координаттар жүйесін анықтап O XY белгілі формулалар бойынша буындарын абсолюттік бұрыштарын табамыз.

Енді алты буынды Стефенсон тетігін кинематикалық схемасының екінші түрін бақылаймыз (2-сурет).

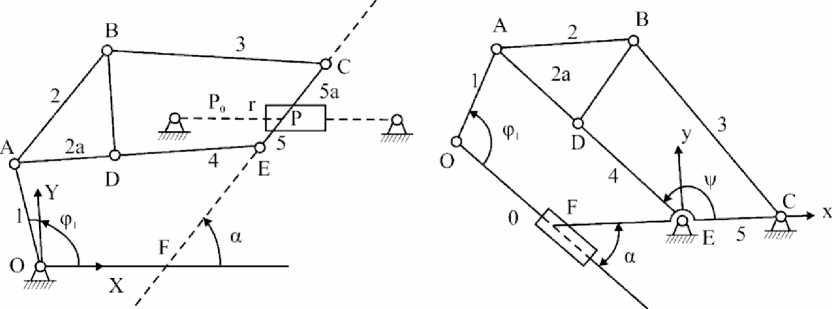
схемасының

а)

2 сурет - Алты буынды Стефенсон тетігін кинематикалық б) салыстырмалы қозғалыста

б)

екінші түрі: а) абсолютті қозғалыста,

О-Х-У координат жүйесінде О тіреу координаттарын берілген деп санаймыз, О-Х осімен Е және С топсалар арқылы өтіп F HYKTeciHge киылыекан TY3y а бурышты береді, және l ОА , l АB , l АД , l ВD , l ВС , l DE, l СE буындарының ұзындықтары. ТША -ның бастапқы орналасуының тапсырмасын табамыз. Сонда қосушы координаттарының топсасының A, B, C, D, E және бұрышының кез келген қатысты звеноны шартты деп санаймыз. Бүкіл тетікті Е-Х-У координат жүйесіне қарай бақылаймыз, ол беcінші звеномен байланысқан, жане С нүктесі абцисса осімен өтетін болсын. Жиынтық координаталарын бурыш ^ -мен 4 жэне 5 буындар арасын қабылдаймыз (2 б-сурет). Д, C бекітпелерін l _ДC векторы арқылы қосамыз, ол былай аньщталады: х_с = 1_Дс, у_с = 0, X d = l_DE • cos y , У_D = l_DE • sin ^ , ^lDC = V^{( X}C ^{- X}D ) ^{+ ( У}С ^{- У}D ) ,

^dc = arctg

Уc - УD

^XC - ^XD

, индекс

"(5)" дегеніміз,

шартты түрде 5-ші буын тіреу ретінде

қабылданды         (2

^ be>c = ± arccos

1 2 BD + 1 2 DC - 1 2 BC

DC BD

б-сурет).

бұрышын

аны^таймыз, ± белгiлерi B-D-C тобыныц бүрмелеуін анықтайды. Онда B нүктесінің

жағдайы    салыстырмалы

^DB=^DC+^bDc ,

^xb ]_[ ^xD I,?     cost ^ DB )

=       ^{+ l}BD •

.У в J  L У D J       L sin( ^ DB ).

^?D B = ± arccos ;

¹ BD ⁺ ‘ AD ^lBB

'll *1 ВD AД

қозғалыста

анықтаймыз,

± белгiлерi А-D-B бYрмелеуiн аныктаиды. А

нүктесінің     жағдайы

салыстырмалы

қозғалыста:

хА

L у a J

xВ

L y В J

+ lAB

^c os ⁽ ^ D⁵B ± ^ A⁵D в ) . sinc ^ DB ± y AD b )

. Бекітпе

центрі A және радиус lОА -ның шеңбермен тендеук (x - xA )2 + (y - у А )2 = /ОА. Тап цалFан нүкте арқылы өтетін төтесінің теңдеуі (x, y) және тап қалған y = k1x + b төтесімен құрайтын тап қалған бұрышы :

У ^- У 1

k ± tg a

1 + k_xtg a

( x - x 1 ), (1)

Онда F(- 1 _FE , 0) HYKTe арцылы ететш a бұрышпен берілген сызыққа y = 0, координаталық жүйеде Е-x-y топсалардан C, Е отетін, былай болады :

у = ± tg a • ( x + l ^ )      ⁽²⁾

Түзу мен шеңбермен қиылысу нүктеле-рін табу үшін (2) және (1) арасына қоямыз, сосын «х» бойынша квадраттық теңдеу ала-мыз:    (x - xA )2 +(± tga(x + lpE )-yA )2 = lOа , бұны шешіп және (2) буынды ескеріп O(xо,yо) кординаттарын табамыз.

Енді O-X-Y координат жүйелерінің абсолют қозғалысына өтеміз, салыстырмалы қозғалыстың формулаларын абсолют қозға-лысца кeлтiрeмiз. ^ бурышынын цабылдаFан мағынасы үшін A, B, C, E-нің шынайы коор-динаттарын жэне ^ бурышын аныцтаймыз: fXa = (Xa -Xo)cosa + (yA -yo)sina 1 Ya = (Xa -Xo)sina + (Уа -Уо)cosa , fXb = (xb -xo)cosa + (ув -yo)sina 1 Yb = (xb -xo)sina + (ув -yo)cosa fXc = (xc -xo)cosa + (yc -yo)sina

1 Y_c = ( x_c - x_o )sin a + ( y_c - y _o)cos a f ^XD = ⁽ x D ^- x o ^{)cOs a + (} y D ^- У_о ^{)sin a} 1 Y d = ( ^XD - x o )sin a + ( y D - y o )cos a f X e = ( x_E - x_o )cos a + ( y_E - y_o )sin a 1 Y_e = ( x e - x o )sin a + ( У е - y o )cos a

Топсалардың координаталарын анық-тап A(X А ,Y А ), B(X В ,Y В ), C(X С ,Y С ), E(X Е ,Y Е ), D(X D ,Y D ) OXY координаталық жүйеде белгілі формулалар бойынша барлығын буындары-ның көлбеудің бұрыштарын табамыз.

Тетік параметрлер мысал, мән үшін (келесі өлшем қабылдаймыз: м, секунд): табанды кривошиптің координаталары X 0 =0.0, Y 0 =0.0; буындардың ұзындықтары L OA = 0.17, L AD = 0.20, L AB = 0.17, L BC = 0.50, L DE = 0.39, L CE = 0.20, Y E =-0.12, Y C =-0.05; бурыш a = 0.0, бурыш L AD жэне L AB буынның арадағы тең 88⁰. Кривошиптің бурыштыц жылдамдыцты to = 200 c ^{- 1} цабыл-даймыз; кривошип 1 айналудың толық айналымын жасайды.

Үшінші суретте A, B, D, C, P коорди-наталары; төртінші суретте - 2, DE, BC буын-дарын жылдамдығы және бұрыштық жылдам-дығымен үдеулері; бесінші суретте –A, B, D, C, E, P нүктелердің үдеулері көрсетілген.

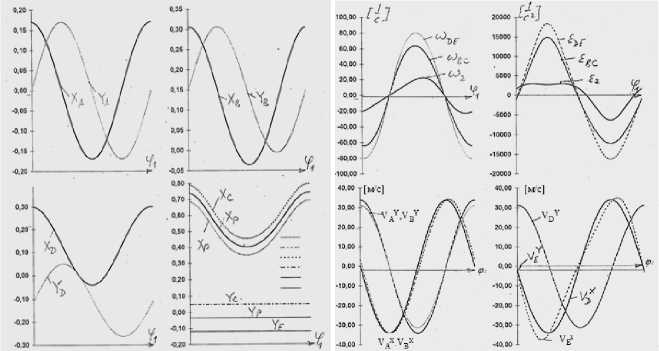
3 сурет – Нүкте орын ауыстыруы

4 сурет - Нүкте жылдамдығы мен удеуі

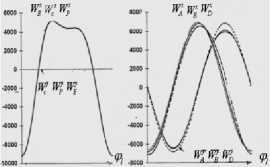
5 сурет - Нүкте үдеуі

Қорытынды

Осылай осы жұптар мен екінші тетіктер үлгісінде

жұмыста қатарлы

айналмалы

ІҮ класты

бастапқы күйде орналасу әдісін зерттеген. Ол қарапайым талдау арқылы осы тетікдердің буындар күйінің сәйкестігін тапты.

ЖКТ буындарының

ӘДЕБИЕТТЕР ТІЗІМІ

• 1.    Джолдасбеков У.А. Графоаналитические методы анализа и синтеза механизмов высоких классов.- Алма-Ата: Наука, 1983.- 256с.

• 2.    Джолдасбеков У.А., Байгунчеков Ж.Ж. Аналитическая кинематика плоских рычажных механизмов высоких классов. - Алма-Ата: КазГУ, 1980.- 102с.

• 3.    Абдрахимов У.Т. Численные методы анализа и синтеза многоконтурных механизмов высо-

  ких классов. Диссертация ... доктора технических наук, Алма-Ата, 1993. 327 с.

• 4.    Джолдасбеков У.А., Абдрахимов У.Т., Бижанов А.Х. Определение функции положения одного механизма третьего вида. //Сб. научных статей КазГУ "Рычажные механизмы и манипуляционные устройства", 1990. -235 с.

• 5.    Джолдасбеков У.А., Темирбеков Е.С. Некоторые аспекты анализа и синтеза механизмов высоких классов.- Астана: Акмолинский ЦНТИ, 2006.- 299с.