Existence and uniqueness theorems for a differential equation with a discontinuous right-hand side

Consider an initial value problem:

X (t) = f ( t,x),   x(a) = x o ,    t E [a, b],                              (1)

where f ( t,x ) can be discontinuous. Classic definition of a solution is too restrictive for differential equations with discontinuous right-hand side. There are different ways to generalize the notion of a solution in this case: Caratheodory solution, Filippov [1, 2] and Krasovskij [3, 4] solutions (based on differential inclusions), Hermes solution [5] (uses limiting transitions) and others (see [2, 6, 7, 8, 9] and references therein). In this paper we consider only Caratheodory solutions. A function x(t) is called a Caratheodory solution of problem (1), if it is absolutely continuous, equality X ( t ) = f (t,x(t)) holds for almost every t E [a, b] and x(a) = x o .

We say that a function f ( t, x) satisfies the Caratheodory conditions in a domain D if in the domain

• C1) f ( t,x) is continuous with respect to x for almost every t ;

• C2) f ( t, x) is measurable with respect to t for each x ;

C3) there exists an integrable function m ( t ) such that | f(t,x) | C m(t) .

(0 2022 Magomed-Kasumov, M. G.

The following results are well-known (see [2, 10]).

Theorem A. Let f (t, x) satisfy the Caratheodory conditions in D = [a, b] x [x g — c, x g + c] . Then there exists a Caratheodory solution of problem (1) on [a, a + d] , where d is such that

t

0 < d ^ b — a,

^ ( a + d ) ^ c,

V ^{( t )} = J

m ( s ) ds.

a

We say that f satisfies L) condition in domain D = [a, b ] x [x g — c, x g + c] if

L) there exist an integrable function l(t) , such that for almost every t E [a, b] and every x , y E [x g — c, x o + c]

^{| f (t,x)} - ^{f (t,}y^{) |} <  ^{l(t) | x} - y | .                                      ⁽³⁾

Theorem B. Suppose f satisfies L) in domain D = [a, b ] x [x g — c, x g + c] . Then if in the domain D a solution of problem (1) exists, it is unique.

Thus, if f (t,x) satisfies in D = [a, b] x [x g — c, x g + c] the Caratheodory conditions and condition L) then there exists a unique solution of problem (1) in [a, a + d] where d satisfies (2).

• I. Sharapudinov obtained another conditions for existence and uniqueness of a solution of problem (1). Before stating the main result obtained in [11], we give some definitions.

Let L p^ [a, b] be a space of functions, integrable with weight ^ on the segment [a, b] :

b

L p [a,b] = f :

| f (t) | ^p ^(t) dt <  to > .

a

By W L p [a, b] we denote a space of (r — 1) -times continuously differentiable functions f = f (t) defined on [a, b] such that f ^(r-1) (t) is absolutely continuous and f ^(r) E Lpi [a, b] .

Let Ф = { ^ k , k = 0,1,... } be a complete orthonormal system in L ^ = L ^ [0,1] . Define a new system Ф 1 = { ^ i,k } using formulas:

t n,g(t) = 1,

^1,1+k(t) = j(t — x) ^k(x) dx, k > 0.

a

This system is orthogonal with respect to Sobolev-type inner product (12), where r = 1 (see details in section 3). Suppose that the system Ф 1 = { ^ i,k } possess the property к(Ф 1 ) = ( ^ ^ L 1 J Ob ^ 2 k (t)^(t) dt) ¹/² <  to . Systems with this property exist (see [12]). The following theorem was proved in [11].

Theorem C. If for some δ the conditions

• A)    f (t,g(t)) E L ^ [a, b] for any function g(t) E W L 2 [a, b] ;

• B)    for any g 1 (t), g i (t) E W L 2 [a, b] the following relation holds:

bb

j ^{[f (t,}g 1 ^{(t)) — f (t,}g i ^{(t))] 1} ^^(t) dt <  ^ ² j ^[g 1 ^{(t) —} g i ^{(t)] 1} ^^(t) dt; aa

C) 5к(Ф1) < 1, hold then initial value problem (1) has a unique solution x(t) E W^2 [a, b]. This solution can be represented as a uniformly convergent series

∞

x(t) = x o + ^c i,k ^ I,k (t), t G [a, b].                               (5)

k=i

In this article, we show that in the case of unit weight ^(t) , using the methods from [11-13], we can

• 1)    remove condition C) in Theorem C;

• 2)    replace condition B) with

B’) there exists an integrable function w(t) , such that for any g i (t),g 2 (t) G W L 2 [a, b] the following relation holds:

bb

I ^{[ f ( t,} g i ⁽t T) ^{- f (t,}g 2 ^{(t))] 2} dt ^ Iw ^{( t ) [} g i ^{( t ) -} g 2 ^{(t)] 2} dt.

Namely, the following theorem holds.

Theorem 1. If f satisfies conditions A), B’), initial value problem (1) has a unique solution x(t) G W ^ [a, b] on [a, b] .

A proof of this theorem, which is given in section 5, is based on using the next theorem.

Theorem 2. Let Ф = { ^ k } be a complete orthonormal system in L ² [u, v] such that for

Ф 1 = { ^ i,k } a condition 5(Ф 1 ) = (sup t _{G [}u,v] £ £ = ^k (t)) ¹/² <  to holds.

If f satisfies A), B’), then for any a G [a, b) and any h ^ b — a that satisfies the condition a+h v-u

w(t) dt < 5^)

α an initial value problem x‘(t) = f (t,x), x(a) = xo, t G [a, a + h], has a unique solution x(t) G WLi2 [a, a + h] on [a, a + h]. This solution can be represented as a uniformly convergent series

∞

• x(t) = xo + V ci,k^i,k(0(t)),   9(t) = ^-^(t — a) + u, t G [a, a + h].

h k=i

A proof of Theorem 2 is given in section 4. The proof is based on using Fourier series with respect to Ф 1 -type system, orthogonal in Sobolev sense and generated by an ordinary system. Some general information about these systems we give in section 3.

Coefficients c i,k in (8) are Fourier coefficients with respect to Sobolev system Ф^ To determine the coefficients c i,k , we use a specially constructed operator A (see (26)), defined in Hilbert space I 2 , consisting of sequences C = ( c j ) ° =i with the norm ||C || = (^j= i c ^)^ • The operator A is constructed in such a way that its fixed point is a sequence of the coefficients c i _,k . In this connection, the question of whether the operator A has a contraction property becomes important. It turns out that a positive answer to this question can be given when functions of the system Ф 1 have the following property

• •    under conditions of Theorem C: к(Ф 1 ) <  to [12-14];

• •    under conditions of Theorem 2: 5(Ф 1 ) <  to (see section 4).

• 2.    Relationship Between Conditions

It was shown in [12] that the properties к(Ф 1 ) <  то and 5(Ф 1 ) <  то hold for the system of functions x i,k (x) generated by the Haar system, and for the system of functions generated by the system of cosine functions.

It should be noted that under conditions of Theorem 2 the operator A is contractive. This property can be employed to construct robust, fast and easy to implement numerical methods of solving an initial value problem with discontinuous right-hand side.

We begin with considering a relationship between conditions C1), C2), C3), L) and A), B’).

Let’s introduce modifications of conditions C3) and L) in the following way:

C3’) there exists a function m(t) E L 2 [a, b] such that | f (t, x) | C m(t) .

L’) there exist a function l ( t ) E L 2 [a, b] , such that for almost every t E [a, b ] and every x , y E [x o - c, x o + c]

^{| f (t,x)} - ^{f (t,}y^{) | C l(t) | x} - y | .                                      ⁽⁹⁾

These conditions differ from their counterparts only in that here we require functions m(t) and l(t) to be from L ² [a, b] .

Theorem 3. A function f (t, x) satisfies conditions C1), C2), C3’), L’) if and only if it satisfies conditions A) , B’) .

This theorem proof is based on the following lemmas.

Lemma 1. If f for some function w(t) satisfies the condition B’) on the segment [a, b] , then f will satisfy this condition with the same function w(t) on any subsegment [а, в] C [a, b] .

• < 1 Let g i ,g 2 be arbitrary functions from W L 2 [а, в] • Denote by g i the continuous extension of g 1 by the constants to the entire interval [a, b] :

  g i ^(a),

  
  

  ^g i ^(x) = g i (x),

  
  

  gnU^t

  
  

  x E [a, а), x E [а, в], x ^{E (e,b]},

  
  

and by g 2 (x; h) the continuous extension of g 2 by constants g i (a) , g i (в) on the segments [a, а — h] , [в + h, b] and by linear functions on the segments [а — h, а] , [в, в + h] :

д1(а), g2(a)hgi(a) (x - а) + g2(а), g2(x; h) = < g2(x), g1 (β)-g2 (β) h     (x чд1(в), - в) + д2(в), x E [a, а - h], x E (а — h, а), x E [а, в], x E (в, в + h), x E [в + h, b].

It is clear that g i (t) and g 2 (t; h) belong to W^₂ [a, b] for any sufficiently small h . Further, for any small h > 0 we have

βb

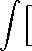
^f(t,g i ^{(t)) - f(t,}g 2 ^(t))] dt ^C Iff ^(t,g i ^{(t)) - f(t,g} 2 ⁽t;^h))] dt

αa

C

bβ

I w(t)^g i (t) - g 2 (t; h)] dt = ^w^g i Ct) - g 2 (t)] dt + I i (h) + 1 2 (h),

a

α

where

α

b

I i (h) = У w ( t ) [g i (t) - 9 2 (t; h)] dt,   1 2 (h) = j w(t) [g i (t) - 9 2 (t; h)] dt.

a

Consider I 1 (h) :

β

α

| I i ^{(h) |} = У w ^{( t )} [g i ^(a)

-

9 2 (a) - g i (a)

h

(t - a) - g 2 (a) dt

α - h

= (g i (a) -

α

g 2 ^{(a)) 2} У ^w(t) 1

-

α - t h

- 2

dt C (g i (a)

-

g 2

α - h

α

(a)) ² У | w(t) | dt.

α - h

Last integral vanishes as h ^ 0 (absolute continuity). Hence, I i (h) ^ 0 , h ^ 0 . Similarly, we can show that 1 2 (h) ^ 0 , h ^ 0 . Then lemma’s statement follows from (10). >

Lemma 2. If f satisfies condition B’), then the function w(t) is nonnegative for a. e. t E [a, b] and the function f satisfies condition L’), in which l(t) = ^w(t) E L 2 [a, b] .

• < 1 Let x , y be arbitrary numbers. By Lemma 1, it follows that for any small h >  0

  u+h

  h У [^{f (t,x) — f (t,}y)]

  
  

  dt C (x

  
  

  u+h

  
  

  u

  
  

  _-

  
  

  ■ h /

  
  

  u

  
  

  w(t) dt,

  
  

  u E [a, b].

  
  

Hence, tending h to 0 , we get that for a. e. u E [a, b] [15, th. 1.3, p. 104]

^{| f(u,x) — f(u,}y^{) | 2 C w(u)(}x ^— y^{) 2} .                              ⁽¹¹⁾

This implies that w(t) must be nonnegative for a. e. t E [a, b] . Then to obtain L’) it remains to extract square roots from both sides of (11) and denote l(u) = ^w(u) . >

• <    Proof Of Theorem 3. Suppose f satisfies the conditions C1), C2), C3’), L’). Arguing as in [10, Chapter VIII, § 8] (or in [16, Chapter III, § 10, Supplement II, p. 122]) one can show that f (t, g(t)) E L ² [a, b] for any measurable function g(t) , so condition A) holds for f . Further, it follows from L’) that

  b

  j [f (t.g i (t))

  a

  
  

b

^{— f(t,}g 2 ^(t))] dt ^C yw^(t)[g i ^{(t) —} g 2 ^(t)] dt,

a where w(t) = l2 (t) E L1[a, b], and condition B’) also holds for f. Thus, conditions C1), C2), C3’), L’) imply conditions A), B’).

Now we show that the converse is also true. Condition C2) follows from A). By Lemma 2, condition B’) imply L’). It follows from L’) that f (t, x) satisfies C1). It remains to show that f (t,x) satisfies C3’). We claim that L’) and A) imply C3’). Indeed, using L’) we get

|f (t, x) — f (t, a)| C l(t)|x — a| C l(t)(b — a), x E [a, b], where l(t) E L2[a, b]. This can be rewritten as f (t, a) —l(t)(b—a) C f (t,x) C f (t, a)+l(t)(b—a). Hence,

| f (t, x) | C m(t) = max {| f (t, a) — l(t)(b — a) | , | f (t, a) + l(t)(b — a) |} , x E [a, b].

Since f (t, a) E L 2 [a, b] (due to A)), we have f (t, a) ± l(t)(b — a) E L 2 [a, b] , so m(t) is also from L 2 [a, b] and condition C3’) holds. >

• 3.    Sobolev Orthogonal Systems

In [17–20] I. Sharapudinov considered systems of functions orthogonal with respect to Sobolev-type inner product

Г - 1

( f,g ) = Ef ^(v) (a) g ^(v)

v=0

b

(a) + j f ^(r) (x) g ^(r) (x) ^(x) dx.

a

He introduced systems Ф _г = { ^ _r,k } defined as

, x    ^(x - ^{a) k}     ,

V r,k ( x ) = ---k!---, k = 0,1,...,r - 1,

k ^{( x )} = ( r - 1)!

x

j (x — t) ^r— 1 ^ k-_r (t) dt,    k = r, r + 1,...,

a

where Ф = { ^ k } ^ =o is a system, orthogonal with respect to the ordinary inner product of the form

b

( ^f,g ) = yf ⁽ t ) g ^{( t )} д(') dt,                                   ⁽¹⁵⁾

a and showed orthogonality of these systems with respect to inner product (12). The system Фг is called a Sobolev orthogonal system generated by the system Ф.

A Fourier series of a function x(t) in the system Ф _г has the following form [18]:

^r—1              п\^к ~

x ( t ) - V'/   . \^ c r,k (x_K k (t),

k!

k=0                    k=r where

b

C r,k (x) = j x ^(r) (t)^ k — r (t) ^(t) dt.

a

The Fourier series of form (16) turned out to be a natural and very convenient tool for solving systems of differential equations [12]. In [12–14] it was proposed an iterative method for solving an initial value problem for a nonlinear ordinary differential equation of the form

x‘(t) = f (t, x), x(a) = xo,   t € [a, b], based on a representation of the solution of problem (18) as a Fourier series in a Ф1-type system:

∞

x(t) = x(a) + ^2 C i,k (x)^ i,k (t),                                (19)

k=1

where x(a) = x o is an initial value and c i,k (x) are unknown Fourier coefficients that should be found.

In already mentioned works [12–14] it is assumed that a function on the right-hand side of a differential equation is continuous in both variables and satisfies the Lipschitz condition with respect to y . However, it turned out that the method used there can be extended to the case of differential equations with a discontinuous right-hand side [11]. We use this method to prove Theorem 2.

• 4.    Proof of Theorem 2

If we introduce a function y(s) = x(9 i(s)), where 9 1(s) = Vs—uh + a, then problem (7) can be written as follows y‘(s) = F(s,y), y(u)= У0, s € [u,vL

where F ( s,y ) = v - hu f ( 9 ⁱ (s),y) . It is easy to verify that F (s,g(s)) € L ² [u, v] for any g € W L 2 [u, v] . Indeed, using the substitution s = 9(t) , we obtain

v

IF ² (s,g(s)) ds =

v

u

h

u

a+h

J f ² (t,g(9(t))) dt.

α

Assuming

g(9(a)), t € [a, a), t € [a, a + h], t € (a + h, b],

g(t) = p(9(t)),

_g(9(a + h)), and noting that g(t) € W^ [a, b], from (21) and condition A) we get

v

IF ² (s,g(s)) ds ^ u

b

—— [ f ² (t,g(t)) dt <  ^ . v - u J

a

Further, for problem (20) following the work [11] we introduce the operator A , the construction of which is based on the following relations:

∞

y(s) = y(u) + 52 С1,к+1(У) Vi,k+i(s), k=0

∞ y‘(s) = 52 ci,k+i(y) vk(s), k=0

∞

q(s) = F (s,y(s)) = Z ck (q) Vk(s), k=0

where the first relation is the Fourier series in the system { v i,k } of the function y(s) € W ^ 2 [u, v] , and the second and third ones are Fourier series in system { v k } of functions y' ( s' ) € L ² [u, v] and q(s) € L ² [u, v] respectively. Note that in the relation (22) the Fourier series converges uniformly (see, for example, [18, Theorem 2.2]), and in (23) and (24) series converge in the metric of L ² [u, v] (due to the completeness of the system V k in the space L ² [u, v] ).

It follows from (7), (23) and (24) that

v

C i,k+i (y) = C k (q) = У F (s,y(s)) V k (s) ds.

u

Combining this equality with (22) we obtain the relation ci,k+i(y)

= 1 ^F^^s, y ^{( u ) +} ZL c i,j+i ⁽y⁾ V i,j+i ^(s)) V k ^{( s ) ds} ,

k ^ 0.

The right-hand side expression is the aforementioned operator A that takes the point d ∈ l2 to the point A(d) G l2 according to the following rule v∞

A(d) =   / F( s,y(u) + ^d j ^ 1,3 +i (s) j^ k (s) ds, k >  0 ,

F ( s,y ) = ~ff (9 ⁱ (s),y) , 9 ⁱ ( s ) = s— uh + a. v - u                     v - u

It follows from (25) that the Fourier coefficients sequence C (y) = (c i,k+i (y), k ^ 0) of the solution y ( s ) with respect to the system Ф 1 = { ^ i k (s) } is a fixed point of the operator A : A ( C ( y )) = C ( y ) .

We now show that A is contractive provided B’).

Let d ¹ and d ² be two arbitrary points in l ² . We introduce the notation:

∞∞ gi(s) = y(u) + 51X1 nj+i^), g2(s) = y(u) + 52 d2 Vi,j+i(s)-          (27)

j =0                                j =0

Theorem [18, Theorem 2] implies that g i ,g 2 G W L 2 [u,v] and that their series uniformly converge on [u, v] . Consider the difference:

A(d ⁱ ) - A(d ² ) =

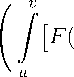
^s, g i ^(s))

-

F (s,g 2 (s))] V k (s) ds, k ^ 0

)

By Parseval’s equality, we have:

№) - A(d ² ) || ,² ₂ = У [F(s,g i (s)) - F ( s,g 2 (s))] 2 ds = J.              (28)

u

Changing the variable s = 9(t) reduces the integral J to the form:

α + h

J = v-u / [f(t,gi(t)) -f(t,g2(t))]2dt, α where gj(t) = gj(9(t)), j = 1, 2. It is obvious that gj(t) G W^2 [a, a + h], j = 1, 2. Since f satisfies condition B’) on the segment [a, b], using Lemma 1 and making the inverse change t = 9-i(s) we get

α + h                                    v

J ^ v-u / ^w(t)[g i ^{(t) -} g 2 ^(t)] 2 ^dt = ( _v - _u ) ₂ j^{w ( 9} - ^{i (s))}[g i ^{(s) -} g 2 ^(s)] ^{2 ds} -     ⁽²⁹⁾

αu

Substituting the expressions from (27) into the last integral and applying the Cauchy–Buny-akovsky inequality we obtain:

v

α + h

w(t) dt.

α

j w⁽⁹ - ^{i (s))}[g i ^(s) - g 2 ^(s)] 2 ds ^ H d - d ² ^ 2 2 ^d 2№ ) v-hu u

This inequality with (28), (29) yields:

l A ( d ⁱ ) - A(d ² ) ^ i 2 ^ №)

( a+h       x 1/2

/ ^{w(t) dt})     li d ¹

α

-

d ² | l 2 *

Therefore, under the condition (6), the operator A will be contractive.

Hence, since l ² is a complete space, the operator A will have a unique fixed point. This point as noted above (see (25)) is a Fourier coefficients sequence of the solution y ( s ) for problem (20). So a solution exists and has a form (22), where C (y) = (c i,k+i (y), k ^ 0) is a fixed point of A . The solution uniqueness follows from the fact that any solution y (s) of problem (20) belongs to the space W L 2 [u, v] and therefore can be decomposed into uniformly convergent series (22), in which the sequence of coefficients is a fixed point of the operator A .

If y ( s ) is a solution of problem (20), then x(t) = y ( 6 ( t )) is a solution of problem (7) on [a, a + h] .

• 5.    Proof of Theorem 1

To obtain a solution on the segment [a, b], we divide it into m subsegments [ai,ai+i] = [ih, (i + 1)h], i = 0,1,... ,m — 1, where h = bma, m > д2(Ф1)V—u Jb w(t) dt (therefore, on each segment condition (6) will hold). We will successively solve the initial value problems x‘(t) = f(t,x),   x(ai)= xi,o, t E [ai,ai+i],                         (30)

on the segments [ a i ,a i+i ] with initial values defined as follows: x o,o = x o , X i,0 = x i - i ( a i ) , i = 1,..., m — 1 , where X i (t) is a solution of the problem on the subsegment [a i , a i+i ] . Then the solution on the segment [a, b] will have the form:

x(t) = x i (t),     t E [a i , a i+i ], i = 0,..., m — 1.

It is easy to verify that given function is a solution of problem (1). Indeed, x(0) = X o (O) = X o,o = x o , so initial condition holds. It is also obvious that x(t) E W ^ 2 [u, v] - Further, denote by E i C [a i , a i+i ] a set with measure ^(E i ) = | a i+i — a i | such that x i (t) = f (t,X i (t)) , t E E i . If t E E = u m - oⁱ E i then t belongs to some E i . Hence, for this t we have x ‘ (t) = x ‘ (t) = f (t,X i (t)) = f (t, x(t)) . Since ^ ( E ) = b — a , x(t) satisfies (1) almost everywhere on [a, b] .