Фазовые портреты учебной деятельности обучающихся решению задач

„ dP                                                  „ ния этой частоты --. При этом фазовые траектории устойчивой системы будут dt

„                                   „ , dP „ асимптотически приближаться к точке с координатами: P = 1 и --= 0 при не-dt ограниченном увеличении времени. Относительную частоту правильных действий Р можно трактовать как обученность деятельности по решению данного dP типа задач. Скорость изменения    рассматривается как обучаемость.

dt                              '

В кибернетическом подходе можно выделить три характерных типа поведе- ния системы, три режима, в которых может находиться динамическая система: равновесный, переходный и периодический.

Равновесный режим обучающейся системы (ОС) соответствует ситуации, когда ее состояние не изменяется во времени. В этом режиме у состояния не изменяется ни одна из ее «координат». В пространстве состояний системы ее равновесные состояния будут изображаться неподвижными точками. При обучении какой-либо целенаправленной деятельности можно выделить равновесное состояние, которое отвечает состоянию полной обученности этому виду деятельности. Для обучающихся в идеале должно быть одно равновесное состояние полной обученности. В этом состоянии обучающийся решает проблемы или задачи без ошибок в автономном режиме. Это означает, что он адаптировался к деятельности в проблемной среде.

Однако бывают ситуации, когда ОС имеет не одно равновесное состояние, а два и более. Это накладывает ограничения на достижение состояния полной обученности. Обучающийся в процессе движения по состояниям может попасть в промежуточное состояние, не отвечающее полной обученности. В этом случае он будет осуществлять деятельность с внешними ограничениями. Чаще всего ему будет необходима дополнительная внешняя информация для осуществления деятельности.

Определение всех состояний ОС и их характеристик является важной задачей для диагностики динамики учебной деятельности в пространстве обучаемости и обученности, так как это позволяет выявить причины, препятствующие достижению состояния полной обученности. Квазипериодический режим характеризуется тем, что в системе возникают колебания внешней негоэнтропии (информации) и внутренней энтропии деятельности. Причем эти колебания происходят со сдвигом фаз, аналогично колебаниям скорости и координаты в пружинном маятнике. Если проводить аналогию дальше, то скорость, или кинетическая энергия, соответствует внешней информации, а координата, или потенциальная энергия, – энтропии деятельности. При этом деятельность осуществляет не только обучающийся, но и та часть ОС, которая управляет его деятельностью. Именно она подает внешнюю информацию.

Таким образом, ОС – это обучающийся плюс внешний управляющий центр. Задача внешнего управляющего центра – подключать датчик внешней информации о расстоянии до цели [Дьячук (мл.), Дьячук, Николаева, 2009, с.128]. Если ОС переходит в состояние полной обученности данному виду деятельности, то внешний управляющий центр не вмешивается в деятельность обучающегося. При этом суммарный коэффициент обратной связи ОС будет равен нулю.

Вернемся снова к рассмотрению переходного режима. Переходный режим возникает под влиянием изменения внешнего воздействия или изменения внутренних свойств систем. Например, обучающийся выполняет какую-либо учебную деятельность. Если управляющая система изменит управляющие воздействия, то возникнет переходный режим. Переходный режим может возникнуть также при изменении внутренних свойств обучающегося. Например, повысилось внимание к выполняемым операциям или резко изменилась мотивация учебной деятельности.

Эффективное изучение динамики поведения ОС возможно не в любом пространстве ее состояний. При неудачном выборе координат включаемых в пространство состояний (фазовое пространство) движение системы может оказаться непредсказуемым. При этом надо иметь в виду, что траектории ОС в фазовом пространстве не пересекаются, то есть движение системы изображается непере-секающимися траекториями. Семейство фазовых траекторий, изображающих движение системы, называется ее фазовым портретом. Фазовое пространство любой динамической системы плотно заполнено фазовыми траекториями, то есть через каждую точку этого пространства проходит траектория.

Изменяя внешнее воздействие на систему, можно существенно изменять ее фазовый портрет. Число измерений фазового пространства системы называется порядком системы. Для ОС в настоящий момент невозможно указать число степеней свободы или координат, в пространстве которых определяется состояние системы. Однако возможность описывать состояние системы в спроецированном пространстве, несомненно, существует.

Как уже сказано выше, исходя из экспериментальных данных, координаты P – доля правильных действий и dP / dt – скорость изменения доли правильных действий интегрированно описывают состояния обучающейся системы. Фазовые портреты ОС строятся диагностическим программным модулем на основе экспериментальных данных (файлов-протоколов), полученных при динамическом компьютерном тестировании [Дьячук (мл.), Дьячук, Лариков, 2003, с. 314].

Рассмотрим плоскость фазового пространства состояний ОС [Там же], которая dP образуется долей правильных действий P и скоростью изменения этой доли . dt

Фазовое пространство состояний обучающегося в предложенной системе коорди-dP                                  dP нат P и отвечает следующим условиям: 1 >P > 0.5;    ∈ (-∞,∞). На рис. 1.

dt                                                 dt приведены фазовые портреты, полученные экспериментально.

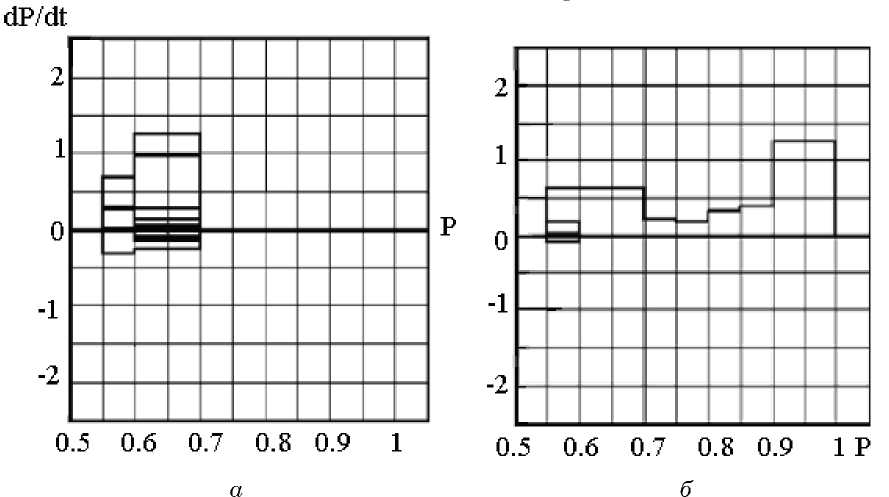
Рис. 1. Фазовые портреты учебной деятельности: а – обучающегося с НСО по математике; б – обучающегося, достигающего полной обученности решению задач по математике. (Вертикальная ось dP / dt имеет цену деления 0.012 с ^{- 1} .)

Фазовые портреты получены из данных динамического компьютерного тестирования процесса научения решению задач по преобразованию графиков функций [Дьячук, 2004, с.156]. Из фазового портрета обучающегося (рис 1а) видно, что доля правильных действий P совершает квазиколебания от 0.5 до 0.7. При dP этом положительная скорость с каждым колебаниям увеличивается, а отри-dt цательная – уменьшается.

Фазовый портрет ОС на рис. 1а отражает квазипериодический режим. Обучающийся «зациклен» на внешнюю помощь и нуждается в том, чтобы внутренняя энтропия его учебных действий гасилась внешней информацией в виде подключения датчика «расстояния до цели». Стоит ОС перевести его на более высокий уровень достижения и соответственно уменьшить частоту помощи, как он начинает совершать неправильные действия. Доля правильных действий уменьшается, и ОС переходит в состояние, отвечающее уровню ниже. Далее все повторяется. Очевидно, что обучающийся не может сделать обощение алгоритма на все множество аналогичных задач. В этом случае наблюдается явление недостаточной обучаемости математике.

Фазовый портрет на рис. 1б показывает, что обучающийся в процессе обучения переходит в устойчивое равновесное состояние, соответствующее полной обу- dP ченности. Траектория стремится к фокусу, то есть к точке P = 1 и = 0 . В этом dt состоянии деятельность обучающегося по выполнению заданий строго упорядочена и безошибочна. Обучающийся на основе анализа и опыта сделал обобще- ния и продуцировал алгоритм решения задачи.

Для диагностики недостаточной специфической обучаемости используют клинический метод динамической оценки [Анастази, Урбина 2003, с. 345]. Одна из первых таких качественных адаптаций процедуры тестирования получила название «тестирование пределов». При этой процедуре тестируемому могут даваться дополнительные сведения или подсказки. И чем больше подсказок требуется для удовлетворительного выполнения задания, тем больше выражена недостаточная специфическая обучаемость.

С точки зрения фазового портрета ОС состояние НСО соответствует «квазиус-тойчивым» предельным циклам. Понятие «устойчивость» применимо не только для оценки устойчивости равновесного состояния системы, но и для оценки ха- рактера движения системы.

Обучающийся как динамическая система, обладающая разумом, имеет единственное устойчивое равновесное состояние, которое характеризуется полной обученностью выполнения деятельности по решению задач. Это состояние соответствует автономной стадии в решении проблем.

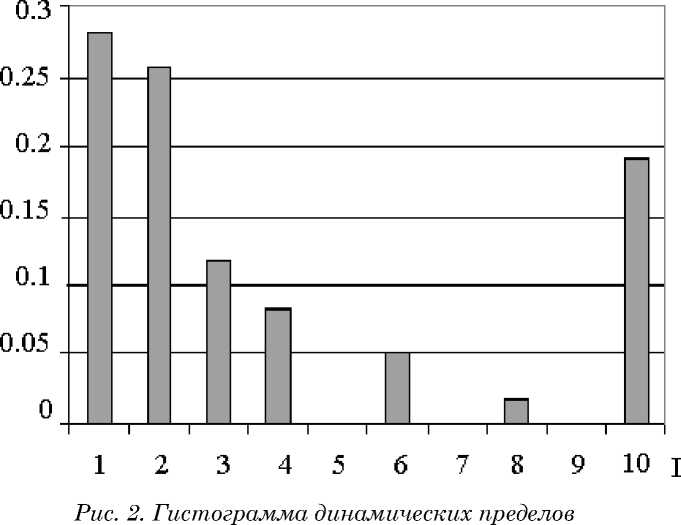
По экспериментальным данным динамического компьютерного тестирования алгоритмической деятельности была построена гистограмма динамических пределов (Бортновский, 2005) на выборке из 319 испытуемых.

ΔN

На гистограмме динамических пределов ось D соответствует доле N обуча- ющихся, имеющих уровень I (N = 319), а ось I соответствует динамическим пределам, достигнутым при выполнении заданий, то есть уровням частоты подкрепления действий обучающихся. Первым динамическим пределом обладают примерно 28 % обучающихся. Это те, кто так и не смог научиться решать задачи без подсказок (каждое действие, выполненное обучаемым, имело информационное подкрепление) и не понимают алгоритм решения задач. Обучающиеся этой группы не могут сформировать инвариантные формы последовательности событий [Хокинс, Блейксли, 2007, с. 75]. Другими словами, они не могут сделать обобщений на основе анализа решения задачи.

26 % обучаемых имеют второй предел – они успешно выполняют задания, только тогда, когда вариативно (случайным образом) в среднем на два действия оказывается помощь. Как только частота помощи уменьшается, обучаемый начинает совершать неправильные действия.

Примерно 21 % обучающихся имеют 7–10 пределы. Это успешные ребята. Они, практически не имея подсказок (10 уровень – одна случайная подсказка в среднем на 100 действий), правильно выполняют задания. Алгоритм решения задач сформирован. Обучающиеся, находящиеся ниже 7 уровня (их 79 %), имеют недостаточную обучаемость математике.

В работе [Дьячук, Шадрин, 2008, с. 623] рассматривалась учебная деятельность по конструированию пазлового пространственного объекта. Итеративное научение состояло в предъявлении одного и того же задания, до тех пор пока обучающийся не исключит ошибки.

Индивидуальные различия обучающихся можно видеть в фазовых портретах учебной деятельности по конструированию пазловых пространственных объектов (рис. 3).

D

Основную роль при выполнении задания играет память, поэтому динамический предел для всех испытуемых равен 10, то есть все обучающиеся достигают состояния безошибочной деятельности, но разными способами. Обучающийся (рис. 3 а) продуцирует информацию методом проб и ошибок (сделал, посмотрел, исправил). Учебная деятельность осуществляется с опорой на внешний контекст или на сигналы из внешней среды. Обучающийся (рис. 3 б) конструирует объект в уме с опорой на внутренний контекст.

Обучающиеся типа (рис. 3 а) получают информацию об объекте, совершая много ошибок и, соответственно, выполняют много раз задание. В процессе адаптации к данному типу действий их обучаемость изменяет свой знак, а обученность совершает квазипериодические колебания.

Сделаем выводы. Показано, что применение метода фазовых портретов позволяет интерпретировать экспериментальные данные динамического компьютерного тестирования и диагностировать индивидуальные различия учебной деятельности обучающихся. В частности, построенная гистограмма динамических пределов показывает, что из 319 обучающихся 79 % с недостаточной обучаемостью математике. Установлено, что недостаточная специфическая обучаемость математике возникает из-за необходимости достижения обучающимися индуктивного порога [Люггер, 2003, с. 547] или осуществления таких операций, как обобщение. Если же для осуществления деятельности достаточно запоминания (памяти), то рано или поздно испытуемые достигают автономности в выполнении заданий, то есть полностью адаптируются к проблемной среде.

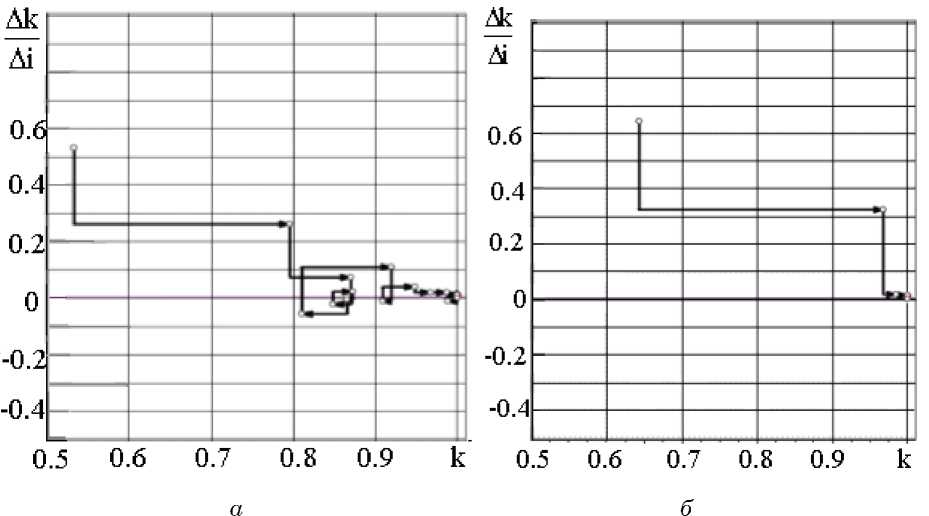
Рис. 3. Фазовые портреты учебной деятельности по конструированию пазлового пространственного объекта. Горизонтальная ось k= 1 - R , где R коэффициент обратной связи между обучающимся и управляющим центром. Вертикальная ось – скорость изменения k в зависимости от номера задания i