Finding Representative Test Case for Test Case Reduction in Regression Testing

Retesting of software is done frequently during the software development lifecycle and in particular in regression testing. In regression testing software grows and evolves that create new test cases and added them to a test suite to exercise the latest changes in the software. Due to many versions of the development of the projects, the possibility of redundant test cases in test suite is more .The redundant test case may in respect to the testing requirements for which they were generated. Due to limitation of time and resource for retesting the software every time before a new version is released, it is really important to search for techniques that ensure manageable test suites size by removing redundant test cases without hampering the performance of the software.

This process is popularly called test suite minimization. The test suite minimization problem [1] can be formally stated as follows:

Given. A test suite T of test cases {t 1 ,t 2 ,t 3 ,…..,t m }, a set of testing requirements {r 1 ,r 2 ,r 3 ….,r n } that must be satisfied to provide the desired test coverage of the program, and subsets {T 1 ,T 2 ,..,T n } of T, one associated with each of the r_i’s such that any one of the tests t j belonging to T_i satisfies r_i.

Problem. Find a minimal cardinality subset of T that exercises all r i’ s exercised by the unminimized test suite T.

The r i ’s can represent either all of the program’s test case requirements or those requirements related to program modifications. A representative set of test cases that satisfies the r i ’s must contain at least one test case from each T i . Such a set is called a hitting set of the group of sets T l , T 2 , . . . , T. A maximum reduction is achieved by finding the smallest representative set of test cases. However, this subset of the test suite is the minimum cardinality hitting set of the T,’s and the problem of finding the minimum cardinality hitting set is NP-complete [2]. Therefore, since we are unaware of any approximate solution to the problem, we develop a heuristic [3,4] to find a representative set that approximates the minimum cardinality hitting set.

The development team if able to find out redundant test case and eliminate them from the test case then the test suite size can be reduced. while finding the representative set the team must ensure that all test requirements are satisfied by the reduced test suite, to make testing more efficient. That is, given the original test suite T={t₁, t₂, t₃, ..., t_n} and a set of test requirements R={r 1 , r 2 , r 3 , ..., r m }, the goal is to find a subset of the test suite T, denoted by a representative set RS, to satisfy all the test requirements satisfied by T. The process of finding the representative set is called test suite reduction [5], [6].

The organization of this paper is as follows. In section II we have specified the Existing Test Case Reduction Techniques. In section III an algorithm based on the genetic algorithm for test case reduction is proposed and discuss. The proposed algorithm is discussed in details followed by its implementation in section IV. The conclusion and future work is discussed in section V.

From Table no 1 the following TR matrix is derived

II. Related Work

The Greedy algorithm [9,10] removes the test case continuously. The algorithm stop when a representative set i.e RS which covers the entire requirement is derived. In Chen and Lau [11] algorithm choose all important test case first then apply greedy algorithm over the remaining test case for rest of test case selection from that. In [5] Jeffrey and Gupta produce representative set for test suite reduction using selective redundancy. Harrold, Gupta and Soffa [1] find representative test cases for each subset and include them in the representative set. In [14] the authors use irreplaceability to evaluate the importance of tests and present an algorithm that ultimately produces reduced test suites with a substantially decrease in the execution cost. Using genetic algorithm in paper [13, 15] the authors are able to minimize test case which cover the entire requirement that can be covered by all the test cases. Izzat Alsmadi, Sascha Alda discuss a method of test case reduction for web service[16] which can be implemented for object oriented program. In [17] Md. Nasar, Prashant Johri, Udayan Chanda discuss resource allocation in software testing. Harish Kumar, Naresh Chauhan [18] give a GA based test case prioritization technique.

/1 1 1 0 0 0\

/ 0 1 111 0

I 1 0 0 0 0 1 j

0 0 1 0 0 1

III. Proposed Ga Technique for Test Case Reduction

Before creation of initial population, the algorithm needs a test requirement matrix. Test requirement matrix (TR) is a two dimensional 0-1 matrix of size ( m * n). The test suite T= { t1, t2, t3 …..,tm} is represented in row and the requirement R={r1, r2,…..,rn} is represented in the column. That is each row of the matrix represent requirements fulfill by a particular test case. Entry into the TR matrix is determined by

TR(W = {0

if ti cannot satisfy rj if ti satisfies rj

In table no1 a test suite of four test case and their six requirements are given. Each test case is representing in row where as the requirement fulfilled by the test case are marked as 1 in the requirement column otherwise 0.

Table 1. An example of test case and requirements fulfill by it

Test case	Requirements to be satisfied
No	r1	r2	r3	r4	r5	r6
t1	1	1	1	0	0	0
t2	0	1	1	1	1	0
t3	1	0	0	0	0	1
t4	0	0	1	0	0	1

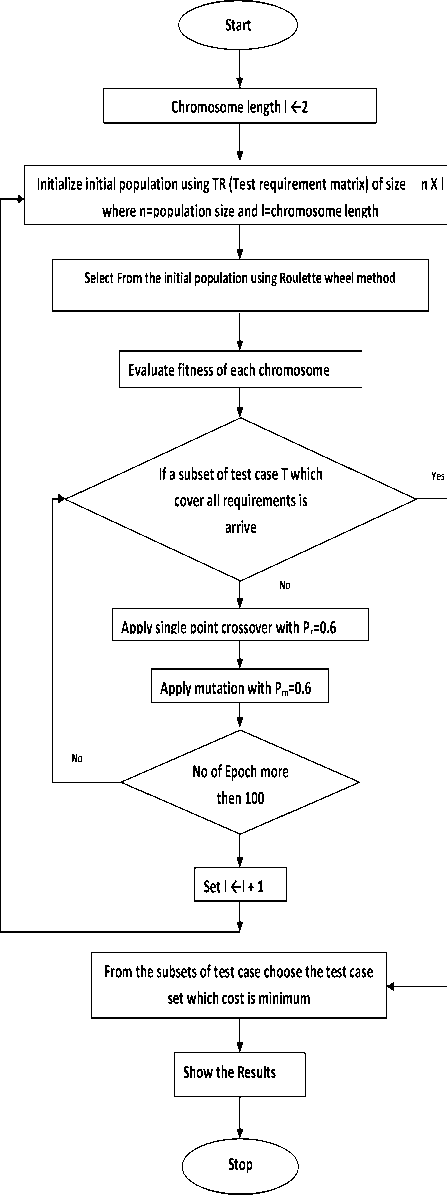
Fig.1. Test case reduction algorithm process.

As for the 0-1 matrix with m rows and n columns, it is essential to select a subset of rows to cover all of the columns in the matrix with minimal cost. Suppose the vector element represents the row i in the vector x is selected and xi=0 means not, therefore, the set coverage problem can be represented as standard optimization problem:

Min z(x)=∑  С Х s.t ∑ а х і ≥ 1 ,i=1,2,3,4,……

(Ensure that every column is covered by at least one row) xj ∈ {0,1} , j=1, 2, 3,……..

The test suite reduction problem is converted to set coverage problem, and then converted to standard optimization problem. The idea of proposed algorithm start from this optimization problem. It is an optimization algorithm that can use genetic algorithm to solve this reduction problem. The GA process is represented in the flow chart given in figure 1.

The algorithm is divide in to two sub algorithm, the first algorithm create population with different chromosome length starting from length two and ultimately call the GA () to find representative set. The GA () method apply selection, crossover and mutation to retune representative set. Then the main algorithm compare cost of the representative set if satisfy stop and return it otherwise it will further generated the new population with chromosome length of one more of size then the previous one.

Algorithm 1 (Test case Reduction)

Input T : the set of test cases

R : the set of requirements

S: the relation between T and R, S={(t, r)| t satisfies r, t ϵ T, and r ϵR} rsi: representative set i rsi ϵ RS

RS : set of representative set(Sub set of T)

Output : Sub set(Representative Set) of T which satisfy all requirements

Begin

RS = { };

i 2

while ( no new rs is generated )

{ rsi GA()

RS=RS U rsi i i+1

}

Calculate cost of each rs return optimal RS;

end

Algorithm 2 GA ()

Input: Initial Population P of size i Output : Representative set of size i Begin j ^ 1 repeat

Pj ^ null;

repeat

Pj ^ Pj U { Randomly from T } until | Pj |=i j until j=i g ^ 1 repeat j^1

repeat

Fi ^ CalculateFitness(Pi) j until j ^ i

P1 ^ ChooseParent(P[random()]).

P2 ^ ChooseParent(P[random()]).

C1, C2 ^ Crossover(pC, P1, P2)

C1 ^ Mutation(pM, C1) C2 ^ Mutation(pM, C2) g ^ g-l until g=dmax return RS of size i

The above algorithm describe how a representative set which is a sub set of T is derived using GA. The first algorithm search a cost optimal representative set using genetic algorithm. The second algorithm which is an elaboration of the GA process describe that when it is called it create representative set of given size.

• A.    Initial Population

Each chromosome of the initial population represents a set of test case i.e a test suite. The initial population is built up randomly using the test case pool. First a population of size two is created which increases gradually till a representative set is not found. We use permutation encoding for encoding the chromosomes. Each chromosome contains a set of test case as given in fig 2

Fig. 2. Chromosome using permutation encoding.

• B.    Selection

We use rank selection to select the chromosome to go to the next epoch. Elitism is used as test show that best population are selected.

C. Crossover

After the chromosomes are selected we applied single point crossover with crossover probability of 0.6 to generate new child from the selected parent.

F(x)=

No of requirment fullfill

X 100

Total no of requirment

F(x) is fitness of chromosome x. The following example gives a clear picture about how it works.

Using the TR matrix, initial population of the algorithm is generated. The algorithm first generate test suite of size 2, 3, 4… . The fitness is calculated for these test suite by performing OR operation of the requirements. For test suite T= {t2, t4}, fitness value will be

t2={0 1 1 1 1 0} t4={0 0 1 0 0 1 }

OR {0 1 1 1 1 1 }

So for the said test suite no of requirement not fulfilled is=1. Total no of requirement =6. Its fitness is =(1/6*100) =83.33%

P1 = and P2 = .

If 1 is chosen, P1 and P2 could be crossed over after the first locus in each to produce two off springs as P1 = and P2=. A crossover selection process is depicted in Fig 3.

D. Mutation

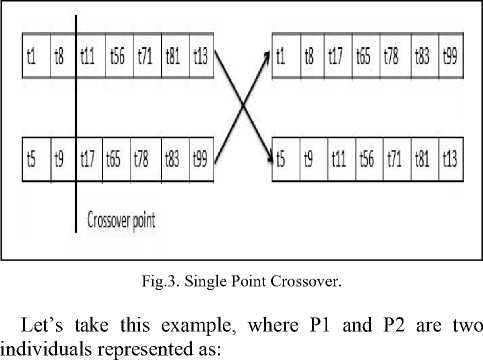
Mutation is used to replace the duplicate test case present in the test suite. For duplicate test case the algorithm randomly select a test case from the existing set that are not included in the chromosome with a mutation a probability of 0.2.

Redundant Test case

t5 t9 t!7 t65 tl7 t83 t99

Replace in mutation

ts

19

t!7

t65

t78

t83

t99

Fig.4. Mutation Operation.

• IV.    Empirical Studies

In order to verify our test suite reduction we take the TR matrix derived from TABLE1.

TR=

1 1 1 0 0 0

/0 1 1 1 1 0 1

1 0 0 0 0 1

0 0 1 0 0 1

From this we select initial population with chromosome length l ≥ 2, 3, 4… m where m is the total no of test case present. In our TR matrix no of test case is 5. The algorithm in each iteration chooses population of size n X l where n is the population length. In every iteration GA is applied over the population. In any iteration if the fitness of one or more chromosome is 100% our algorithm stops. Out of all the chromosome produced by the algorithm we choose that chromosome whose cost is minimum as representative set.

For example by taking population size=5, Pc=0.6, Pm=0.2 from the above TR matrix, we get the following result.

Iteration # 1

l=2

Randomly choose 5 chromosomes of length 2 and calculate their fitness.

Figure 4: Initial population with fitness value of our example.

The fitness value of each chromosome is calculated by performing and operation among all the requirement sets of individual test case.

Then fitness the result is converted into a percentage which denotes how much percentage of requirements is covered by the chromosome. This percentage is calculated using equation no 1.

Initial

Populati on

T1	T4
T2	T4
T4	T5
T5	T1
T2	T3

Fitness value

RS={T2,T3}

The test suite T={T2,T3} gives 100% fitness value that’s why it is the representative set(RS) of T={T1,T2,T3,T4,T5}. Hence our algorithm stops after 1st iteration. For the above example in iteration#1 no cross over or mutation operation of GA needed. In this case the representative set is derived in 1 epoch. Otherwise we have to go for a fixed no of epoch in iteration#1. In the next iteration chromosome length 2 will be increased to 3 and again GA will be applied. This process will continue till RS is produce.

The algorithm is implemented in the working platform MetLab. After getting RS, the test case are run using an environment of JUnit, Ant and Eclipse Emma using IDE e clipse . t able 2 shows the details of subject programs and the collected test case-requirement matrices. Column 1 lists all the subject programs. Column 2 lists the number of lines of code (LOC) of each subject program. Column 3 lists the size of the corresponding subject program’s test suite pool where T denotes the number of all the test cases and R denotes the number of test requirements. Three programs were studied, ranging from 501 to 1114 lines of code (LOC). These three Java programs in our experiment are AVL tree (AVL) with all operation and application, Mutation Tool (MU), transmission control (TC). The feature of these programs has been given in Table 2.

Table 2. Summary of programs used in experimentation

Program	Source file (LOC)	Test suite pool (T X R)
AVL	501	109 X 45
MU	876	112X 87
TC	1114	132 X 85

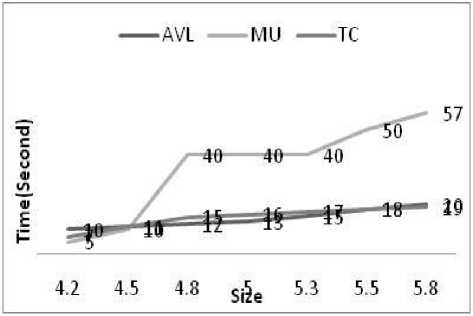
Fig.5. Execution time of the programs

Select Test Suit Size

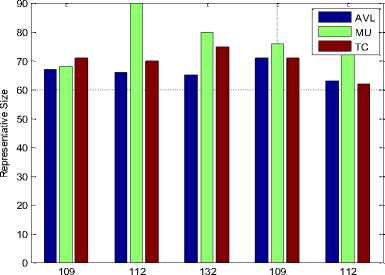
Fig.6. Reduction of test case size in five instance

In figure 5 it is shown that the execution of reduce test case save the time. In figure 6 five instance of of execution of the test case are recorded and seen that all the time the reduce test case size approximately remain same.

The efficiency of the algorithm in terms of time and space complexity is determined in the following graph.In the figure 6 X-axis represents (Number of generation, Population size), Y-axis represents time of execution of the GA algorithm. The test programs are taken in the experiment. The algorithms take maximum 11.66 minute for MU program. The memory requirement is less the 100KB as it is found in the MATLAB implementation of the program.

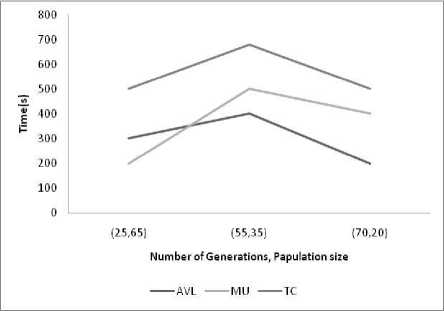
Fig.7. Time and space complexity comparison

• V.    Conclusion

In this paper an algorithm for test cases reduction is presented and implemented. It is compared with other existing techniques. It finds out representative set of the test case from the given set of test case. It uses a simple

GA method to reduce the test case in regression testing. Moreover, the generated test suite is minimized greatly. Therefore it can reduce test cost of regression testing and improve the efficiency of the software with the optimized test suite. The limitation of the implementation is that it is implemented for a program of maximum 1000 line of code which will be implemented with program of more line of code in future.

Acknowledgment

I render my acknowledgement to Prof. (Dr.) Birendra Kumar Nayak for his advice, suggestions, inspiration and guidance for this work. I am also thankful to Gandhi Institute for Technological Advancement, Bhubaneswar for providing research facility in their research lab.