Физическая модель температуры недр земли

Известно, что исследование термического поведения Земли является одним из наиболее умозрительных разделов геофизики. На больших глубинах температура меняется весьма неопределённо. На основании постоянно увеличивающегося со временем массива измерений в разных тектонических областях к настоящему времени определены значения потока тепла через поверхность Земли.

Считалось, что основным источником внутреннего тепла планеты является радиоактивность изотопов урана, тория, калия. Исследования показали, что радиоактивные элементы с сильными литофильными свойствами в основном распределены в коре и не могут определить весь тепловой поток, излучаемый Землей.

По современным представлениям распределение температур в недрах зависит от состава недр и геодинамических процессов. Процессы, происходящие в мантии, связывают с фазовыми переходами, процессы в жидком ядре - с конвекцией и адиабатическими явлениями (Жарков, 1983). В работе О.Г. Сорохтина и С.А. Ушакова (1991) условно определено, что такие параметры, как плотность ρ, температура Т, давление Р и их распределение в недрах, создают физическую модель Земли. Предложен метод исследований, заключающийся в определении теоретической зависимости одной физической величины от другой, которая с большой вероятностью может быть определена экспериментально. Далее показано, что прохождение поперечных (S) и продольных (Р) волн может дать точную информацию о распределении плотности и давления в недрах Земли.

Постановка задачи

Рассмотрим качественную модель распределения температуры в недрах Земли с учетом изменения плотности р вещества. Отметим, что температура Т является мерой средней кинетической энергии атомов в веществе (Трофимова, 2004), и далее определим причины движения атомов.

В работе Ю.П. Петрова, А.В. Киевского, В.И. Костицына (2014) показано, что одной из причин движения атома, изначально находящегося в неподвижном состоянии, является испускаемый им фотон. Количество движения неподвижного атома равно нулю. Также нулю равно и суммарное (ядро+фотон) количество движения атома и после испускания им фотона. Однако фотон движется в одну сторону, а атом, согласно закону сохранения импульса, в противоположную. Атом приобретает кинетическую энергию, а совокупность атомов определяет их среднюю кинетическую энергию в веществе, что и характеризует его температуру. Данная модель удобна для описания броуновского движения в газах и жидкостях.

Рассмотрим причину установления температуры вещества с учетом внутриатомных взаимодействий, зависящих от его плотности.

Интересным представляется высказывание В.Н. Жаркова (1983): «Реальной физической характеристикой среды, характеристикой более осязаемой, чем давление, является расстояние между атомами ...». Эта идея им в дальнейшем не была развита. В данной работе авторы исходят из того, что увеличение плотности вещества вызывает деформацию его атомов.

Методика исследования

Исследования проведены с использованием модели атома Резерфорда - Бора. Кинетическая энергия электрона ( Е к ) е в атоме определяется формулой

( E k ) e = m e V e- , (1)

где me - масса электрона, Ve - скорость электрона.

Второй закон Ньютона для электрона, движущегося в атоме под действием сил

Кулона, имеет следующий вид:

zq

e л      2 =        ’

4п^ rr где r - радиус орбиты электрона, qe - за ряд электрона, ео - электрическая посто янная, z - заряд ядра.

Воспользовавшись первым постулатом Бора (Трофимова, 2004) выраженным формулой

h mever = —n,            (3)

2п определим радиус r на основании (3):

nh

r =--------.

2nmeve

Здесь h - постоянная Планка, n - номер орбиты электрона.

Подставляя найденный радиус r в уравнение (2), получим следующую фор- мулу для вычисления ve:

v . = Z q

2 &₀hn

•

Уравнение (1) с учетом (5) запишется в виде

₍ Е ) = _Z 2 mq

^{( k)e}       8 h²s₀'n ² ’

Для атома водорода ( z = 1, n = 1), принимая m e = 9,109-10 ' ³¹ кг ; q e = 1,602-10^-19 Кл; h = 6,62640 ' ³⁴ Дж•с ; е о = 8,854-10 ' ¹² Ф/м на основании (6) получим значение кинетической энергии [( Е к ) е ] _z =1, n =1 электрона, равное 21,8040 ' ¹⁹ Дж .

Полученное значение кинетической энергии электрона равно величине энергии (Еи)а ионизации атома водорода, которое установлено (Физический энциклопедический словарь, 1983) экспериментально и имеет значение, равное 21,7940'19 Дж.

Относительная погрешность энергии, теоретически найденной по формуле (6) и полученной экспериментальным путем, составляет 0,05%, что находится в пределах погрешностей измерительных прибо- ров. Поэтому в дальнейших расчетах будем использовать теоретическое значение кинетической энергии электрона, равное 21,80∙10-19 Дж.

В этом случае уравнение (6) запишется в следующем виде:

( E k ) e = — [( E k ) e L - 1, n - , -        (7)

n

В веществе тепловое движение атома определяется его кинетической энергией ( E k ) a . Масса m a атома с большой степенью точности определяется массой m я его ядра, т.к. электроны в атомах имеют гораздо меньшие значения массы. Для дальнейших рассуждений примем ( E k ) a = ( E k ) я .

Предположим, что атом в первоначальный момент неподвижен и не излучает фотон. Согласно планетарной модели атома, предложенной Резерфордом (Трофимова, 2004), электрон движется по орбите и обладает в каждый момент времени количеством движения m e v e . Из закона сохранения импульса следует, что равным ему и противоположным количеством движения - m я v я должно обладать взаимодействующее с ним ядро, т.е. m e v e - m я v я = 0. Здесь символы m я и v я соответственно обозначают массу и скорость ядра атома.

Отсюда, с учетом выражения (5), получаем формулу m e яe m я

m e z   q e

---------- ------ . ---------------

• тя n e

Кинетическая энергия ( E k ) a атома с учетом (7) и (8) запишется в следующем виде:

(Ek)а = (Ek). - -ятя = - ' [(Ek)e 1=.,-1-

2 n m„

я

В атоме водорода радиусу r минимальной орбиты электрона соответствует ее номер n = 1. При увеличении плотности вещества объем атома уменьшается за счет приближения электрона к ядру. Поэтому делаем предположение, что значение n будет меньше единицы и обратно пропорциональным величине плотности ρ . Данное предположение запишем в виде отношения

C n - -,                 (10)

P где С - коэффициент пропорциональности, зависящий от среды и внешних условий.

С учетом (10) выражение (9) будет иметь вид

( E k ) _a - z ² P    [( E k ) e 1 z - 1, n - 1 -      (11)

C —„ я

Австралийский геофизик Булен, анализируя распределение сейсмических волн в недрах Земли, разделил недра на ряд зон, для которых ориентировочно был определен химический состав вещества. Согласно В.И. Трухину, К.В. Показаеву, В.Е. Куницыну (2005), принимаем, что твердое и жидкое ядра состоят из железа 56 Fe , а мантия - из силикатов MgSiO 2 - Fe 2 SiO 2 .

В силу этого можно принять осред-ненные значения расчетных величин для твердого ядра (т в . я ), жидкого ядра (ж.я) и мантии (м):

( z ) тв.я = ( z ) ж.я = 26;

( m e / m я ) тв.я = ( m e / m я ) ж.я = 9,82∙10^-6;   (12)

( z ) м = 13,8; ( m e / m я ) м = 3,00∙10^-6.

Заряды z и соотношения масс m e / m я вычислены как усредненные значения на каждый атом среды. Информация для вычисления этих величин взята из справочника ( Физический энциклопедический словарь, 1983).

При тепловом движении атомов, согласно закону Больцмана о равномерном распределении энергии по степеням свободы (Трофимова, 2004), для вычисления температуры   Ттеор,  характеризующей энергию атома, имеем формулу

( E k ) a - i^, ,           (13)

где i - степень свободы атома, k - постоянная Больцмана, равная 1,38∙10^-23 Дж/К .

В твердом ядре Земли атом имеет три степени свободы (i = 3). В жидком ядре атомы дополнительно обладают еще одной степенью свободы, обеспечивающей конвекционное движение (i = 4). Для мантии, состоящей из силикатов, имеющих в молекулах связанное состояние атомов, характерны колебательные движения последних, что отвечает двум степеням свободы (i = 2).

Из равенства правых частей уравнений (11) и (13) для определения температуры вещества в недрах Земли получаем формулу

Т еор = ^{2 2}’ 7 2 ' m e- ^{[( E}k ) < ] " -■ " (14) ik C m я

При вычислении Т Теор по формуле (14) воспользуемся данными о плотности и температуре, приведенными в работе О.Г. Сорохтина, С.А. Ушакова (1991).

Распределение плотности ρ и температуры Т с глубиной Н в недрах Земли
H, км	ρ 103, кг/м3	Т, К	Т Теор , К
1	2	3	4
200	3,30	1770	1109
430	3,60	1940	1320
430	3,82	2010	1487
600	4,09	2130	1704
670	4,16	2170	1793
670	4,37	2110	1946
800	4,49	2170	2054
1000	4,61	2260	2166
1200	4,72	2360	2270
1400	4,83	2450	2377
1600	4,94	2540	2486
1800	5,04	2640	2589
2200	5,25	2820	2809
2600	5,45	3010	3026
2885	5,60	3130	3195
2886	9,52	–	–
3000	10,06	3310	3310
3400	10,60	3830	3675
3800	11,06	4400	4000
4200	11,43	4870	4273
4600	11,72	5280	4492
5000	11,97	5620	4686
5120	12,04	5710	4741
5120	13,00	–	–
5400	13,10	5890	5890
5800	13,23	6060	6007
6000	13,27	6110	6044
6200	13,29	6140	6062
6371	13,29	6140	6062
288	–

В уравнении (14) величина С, зависящая от параметров среды и внешних условий, является неизвестной. Значение

С можно рассчитать, используя метод реперных точек (Трухин, Показаев, Куни- цин, 2005).

Для этого из уравнения (14) находим ipz ik   TТеор

C ■

•      [( E k ) _e ] _z ■!, , ■

m

В реперных точках предполагаем, что температура T и плотность ρ , приводимая в большинстве исследований, численно равны Т Теор и ρ . Численные значения Т и ρ берем из таблицы (Сорохтин, Ушаков, 1991).

Для мантии на глубине порядка 400 км при температурах T = (1600 ±50) К создаются условия для фазовых переходов минералов MgSiO2-Fe2SiO2. Такая температура соответствует плотности ρ = 3,90·103 кг/м3. Вычисления по формуле (15) для мантии дают значение величины См = 0,82·103 (n = 21). Для жидкого ядра при значении Т =3310 К и плотности ρ = 10,06·103 кг/м3 величина Сж.я = 4,00 103 (n = 0,33), а для твердого ядра при Т = 5890 К и ρ = 13,10·103 кг/м3 значение Ств.я = 4,50 103(n = 0,34).

Результаты

В соответствии с вычисленными значениями коэффициентов С и с помощью уравнения (15) проведены вычисления величины Т Теор .

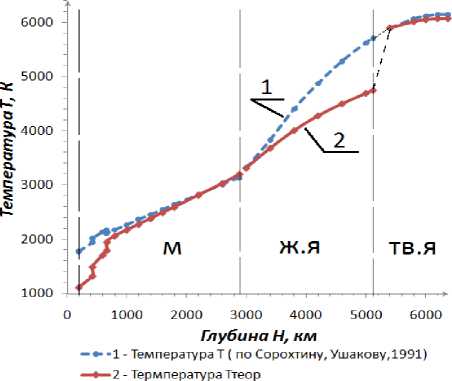
График зависимости распределения температур Т в недрах Земли с глубиной Н

Результаты расчетов Т Теор представлены в таблице (столбец 4), с их использованием построен график зависимости распределения температур в недрах Т Теор Земли с глубиной (рисунок).

Выводы

Результаты исследований показывают, что источником тепла служит изменение (увеличение) плотности пород. Чем плотнее сжата порода, тем выше ее температура, что в конечном итоге сводится к действию закона всемирного тяготения Ньютона.

Полученная зависимость Т теор = f(ρ) для принятой в работе модели имеет резкое изменение температуры на границе жидкое ядро - твердое ядро.

Можно предполагать, что движение литосферных плит в местах их взаимного соприкосновения создает условия, спо- собствующие значительному увеличению плотности пород и повышению температуры, что в свою очередь приводит к образованию вулканов.