Формирование и развитие компетенции инженера в рамках учебной дисциплины в метрическом компетентностном формате

Основным недостатком традиционной образовательной системы является, то, что из-за общей информатизационной глобализации и возрастания сложности инженерных проблем будущий инженер за отведенное время обучения не может на основе имеющихся учебных материалов и учебной деятельности, ограниченных в рамках конкретных дисциплин формате, сформировать в своей когнитивной сфере профессионально-ориентированную единую инженерную компетенцию (как подсистему (организацию) психики). В тоже время владение компетенцией является необходимым и во многом достаточным условием для решения потока сложных проблем в определенном направлении профессиональной деятельности. При этом опыт многих передовых в инженерии стран показывает, что формирование инженерной компетенции целесообразнее организовать в два этапа. Первый этап -формирование общей инженерной компетенции, в определенной направлении деятельности, второй этап (среди лучших из первого этапа) – формирование специальной инженерной компетенции по решению сложных проблем в довольно узкой области деятельности. В целом, это все потребовало организацию двухступенчатой образовательной системы, т.е. подготовки инженеров-бакалавров в определенной направлении, владеющих общей инженерной компетенцией и инженеров-магистров, владеющих специальной компетенцией в определенном направлении деятельности. Владение специальной инженерной компетенцией, должно позволить им решать сложные проблемы, но в узкой области деятельности.

На практике достаточный уровень развития компетенции в определенном направлении внешне выражается, как умение надежно решать проблемы в этом направлении, т.е. в способности инженера используя свою компетенцию через свою деятельность трансформировать профессиональную проблему в продукт.

Из контекста сказанного следует, что учебная дисциплина является главным элементом дидактической системы подготовки инженера, т.к. формирование, развитие и становление инженерной компетенции по определенному направлению и профилю инженерной деятельности происходит через организованную учебную деятельность по решению проблем в рамках дисциплин. На рис. 1 (в стандарте SADT функционального моделирования) [1] показан пример схемы интеграции потоков учебных проблем решаемых через учебную деятельность.

Поток 1 -учебных проблем

ФГОС ВПО, учебные планы, УМК (дисциплины)

Управление

в рамках дисциплины

Результат 1 овладения компетенцией

Учебная

Учебная в рамках дисциплины 1

в рамках дисциплины 2

Поток 3 -учебных проблем

Поток 2 -учебных проблем

Поток 4(1, 2, 3) -w учебных проблем

в рамках дисциплины

Результат 2 овладения компетенцией

Механизм

Учебная

деятельность в рамках дисциплины 3

Интеграция результатов

Результат 3 овладения компетенцией

Учебная

деятельность в рамках дисциплины 4

Интегрированный результ ат (1, 2, 3, 4) овладения компетенцией в рамках дисциплины

в рамках дисциплины

Знания, преподаватели, оборудование программное обеспечение, средства ДО и т.д.

Рис. 1. Функциональная модель интеграции потоков учебных проблем и компетенций, рассматриваемых в рамках дисциплин в единую инженерную компетенцию

В целом, как показано на рис. интегративный процесс, формирования инженерной компетенции происходит следующим образом: через решение учебных проблем (поток 1) и освоение знаний, будущий инженер овладевает частью инженерной компетенции, т.е. он через организованную учебную деятельность развивает в себе способность решать проблемы, рассматриваемые в рамках дисциплины 1. Аналогично, он разовьет в себе способность решать проблемы, рассматриваемые в рамках дисциплин 2 и 3. На этом примере дисциплина 4 является интегрирующей, т.е. там рассматриваются все эти проблемы в комплексе, для решения которых необходимы способности, развитые в рамках дисциплин 1, 2, 3, но они оказываются недостаточными. В результате, через новую организованную учебную деятельность он приобретает знания и развитие способностей, что позволяет в рамках дисциплины 4 сформировать качественно новую часть инженерной компетенции. Разумеется, этот процесс интеграции продолжается до полной сформированности и развитости инженерной компетенции, которая в дальнейшем позволит инженеру решать профессиональные проблемы в определенном направлении деятельности.

Таким образом, инженерная компетенция самоорганизуется как подсистема психики в результате целенаправленной внешней деятельности. Состояние развития компетенции характеризуется уровнями развития способностей в определенном направлении.

В этом интегративном процессе формирования и развития инженерной компетенции через подготовку в рамках дисциплин выделим два кластера:

• 1.    Кластер профессионально-ориентированных дисциплин, предназначенных для развития инженерной компетенции по профилю подготовки.

• 2.    Кластер поддерживающих дисциплин, необходимых для развития инженера как личности, как производственного элемента в социуме, а так же поддержки дисциплин из первого кластера.

В контексте сказанного рассмотрим множество дисциплин, необходимых для подготовки инженеров в направлении «Информатика и вычислительная техника» по профилю «Информационные системы и технологии» (рис. 2). Построим топологическую карту дисциплин, в которой состояние овладения компетенцией у будущего инженера постепенно расширяется во времени за счет освоения последовательности дисциплин из центра к краю.

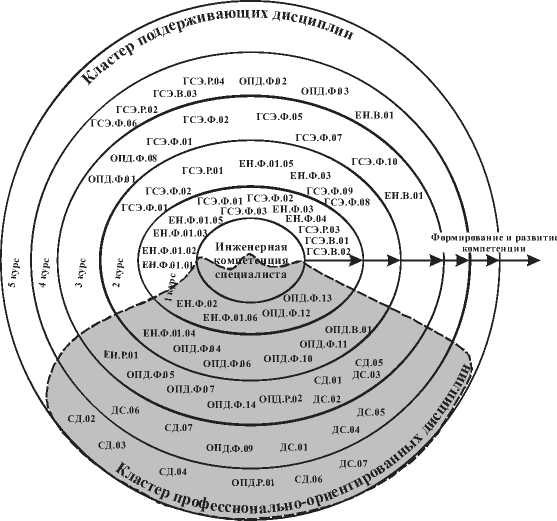
Рис. 2. Модель последовательного формирования и развития инженерной компетенции на основе освоения различных дисциплин (спецификация дисциплин приводиться в приложении)

Разумеется, при такой классификации одна и та же дисциплина, в зависимости от направления и профиля подготовки может попасть в разные кластеры. На рис. 3 рассматривается два направления подготовки: 1) информатика и вычислительная техника; 2) химические технологии. В первом случае дисциплина «Информатика» является элементом кластера профессионально-ориентированных дисциплин, а во втором – элементом кластера поддерживающих дисциплин.

Для того, чтобы дисциплина внесла максимальный вклад в формирование и развитие компетенции в этих направлениях они должны иметь разные законы распределения продолжительности учебной деятельности в рамках этой дисциплины. Очевидно, эти законы могут быть получены только в результате экспертизы.

£5

Наилучшее (экспертное) распределение временных ресурсов в рамках дисциплины “Информатика” для формирования и р азвития компетенции в направлении “Информатика и вычислительная техника ”

Ограничения:

1. Рамки ФГОС ВПО

2. Федеральный интернет экзамен по базовой части

3. Профилизация

£5

Наилучшее (экспертное) распределение временных ресур сов в рамках дисциплины Информатика” для формир ования и р азвития компетенции в направлении “Химические технологии”

Дисциплина “Информатика”

Дисциплина 1

Дисциплина 2

Дисциплина 3

...

Дисциплина N

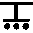
Рис. 3. Законы распределения временных ресурсов развития компетенции в рамках дисциплины «Информатика» в разных направлениях подготовки

Опираясь на модели [2, 3] С.Л. Рубинштейна «Единства сознания и деятельности» и Л.Н. Леонтьева «Общность строения внутренней и внешней деятельности», а также исходя из логики и содержания инженерной деятельности, полученной в результате системного анализа [4] имеем:

• 1.    Эффективность деятельности инженера по решению проблем в определенной предметной области в основном зависит от уровня развития его проектно-конструктивных способностей, и от полноты, целостности его интеоризованных знаний.

• 2.    Подготовка инженера должна быть осуществлена в компетентностном формате, т.е. нацелена на развитие его естественных проектно-конструктивных (АВС) способностей до уровня личностных технологий (специальных способностей), которые в комплексе со знаниями гарантируют успешное решение профессиональных проблем.

• 3.    Метрический компетентностный формат подготовки инженера означает, что эта подготовка проходит в компетентностном формате в режиме мониторинга развития его способностей и интеоризации знаний до уровня достаточного для решения актуальных профессиональных проблем, т.е. развитие АВС-способностей и состояние интеоризованности знаний проходит под наблюдением и управлением специально спроектированной для этих целей дидактической системы до достижения в рамках этой системы определенных значений метрик.

• 4.    Функциональная модель дидактической системы с помощью которой , осуществляется подготовка инженеров в рамках профессионально-ориентированной дисциплины в метрическом компетентностном формате имеет вид, показанный на рис. 4.

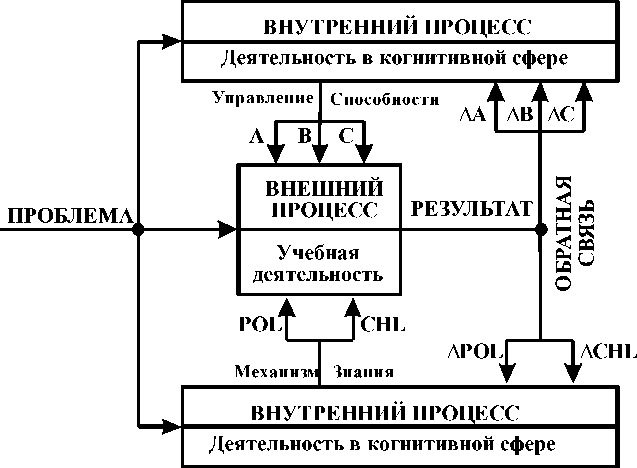
Рис. 4. Функциональная модель учебной деятельности

Согласно этой модели функционирования, для подготовки инженера к решению проблем из определенной области деятельности (в рамках профессионально-ориентированной дисциплины) организуется учебная деятельность по решению учебных проблем, по которой будущий инженер учебную проблему (ПРОБЛЕМА) трансформирует в РЕЗУЛЬТАТ. При этом он проделывает следующие операции развивающие его АВС–способности и дополняющие его знания.

• 1.    Операция А , при которой ПРОБЛЕМА формализуется в когнитивной сфере на основе проблемной ситуации и знаний в этой области. Причем сложившаяся ментальная модель проблемы будет зависеть от адекватности уровня развития способностей; от формализации (параметр А) проблемы; от полноты (параметр POL), а также целостности (параметр CHL) знаний.

• 2.    Операция В , при которой на основе ментальной модели проблемы (проблемной ситуации) строится конструкт решения проблемы (ментальная модель конструкта). Разумеется, ментальная модель конструкта решения будет построена в

• 3.    Операция С , при которой будущий инженер найденный конструкт решения как внешний процесс (через учебную деятельность) реализует в реальной среде. При этом у него в результате аккумулируются все неадекватности и неточности и незнания, которые он допустил при выполнении операций А и В, а также его результат будет масштабирован по эффективности решения уровнем развития исполнительских (параметр С) способностей и знаний.

• 4.    Операция «анализ результата». Очевидно, полученный результат располагается в интервале РЕШЕНИЕ НЕ ПОЛУЧЕНО до ПОЛУЧЕНО ЭФФЕКТИВНОЕ РЕШЕНИЕ.

• 5.    Операция «приращение знаний и способностей». Через ОБРАТНУЮ СВЯЗЬ обучающиеся получают всю информацию о состоянии эффективности своего результата. Будущий инженер в принципе сделал вывод о том, что рассматриваемая проблема находится (не находится) в зоне его ближайшего развития. В случае необходимости, возможности, желания, доступности он занимается учебной деятельностью, чтобы прирастить уровень развития своих АВС–способностей и знаний, т.е.

рамках формализованной модели и зависеть от уровня развития конструктивных способностей (параметр В); а также будет зависеть от полноты и целостности знаний вообще, и в области решения проблемы в частности.

Показатель эффективности Э полученного РЕЗУЛЬТАТА формально может быть записан так

Э=ФУНКЦИЯ(<, >).

Результат РЕШЕНИЕ НЕ ПОЛУЧЕНО свидетельствует о неразвитости АВС-способностей как личностных технологий в организации ведения внутренней и внешней деятельности, а также недостатке знаний как интериоризованного внешнего опыта решения подобных проблем.

Результат ПОЛУЧЕНО ЭФФЕКТИВНОЕ РЕШЕНИЕ свидетельствует о развитости личностных технологий (АВС-способностей) и о достатке интериоризованных знаний для решения проблемы данной сложности. Разумеется для решения другой более сложной проблемы уровень развития АВС-способностей и интериоризованных знаний может оказаться недостаточным.

А(новое значение) = А(старое значение) + ∆ А(приращение)

В(новое значение) = А(старое значение) + ∆ В(приращение)

С(новое значение) = С(старое значение) + ∆ С(приращение)

POL(новое значение) = POL(старое значение) + ∆ POL(приращение)

CHL(новое значение) = CHL(старое значение) + ∆ CHL(приращение)

Итак, с точки зрения внутренней деятельности инженера – компетенция это подсистема психики инженера, которую необходимо формировать за время их подготовки [3].

С точки зрения внешней деятельности, компетенция – это способность решать проблемы в определенной области деятельности [3].

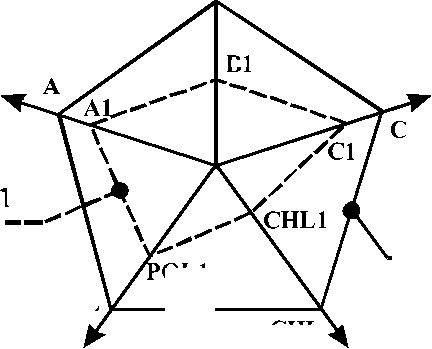
Компетентность определяет требования к эффективности решения проблем в рамках направления деятельности (пороговые значения метрик гарантирующих решение проблем инженером в рамках направления деятельности с определенной надежностью). Принципиальная схема «стоп-кадр» мониторинга формирования компетенции, т.е. метрики состояния компетентности, показана на рис. 5, где в рамках модели дидактического элемента компетентностного формата показано состояние двух будущих инженеров U1 и U2.

В

U1

POL

В1

U2

OL1

CHL

Рис. 5. Модель состояния уровня развития компетенции двух будущих инженеров U1 и U2

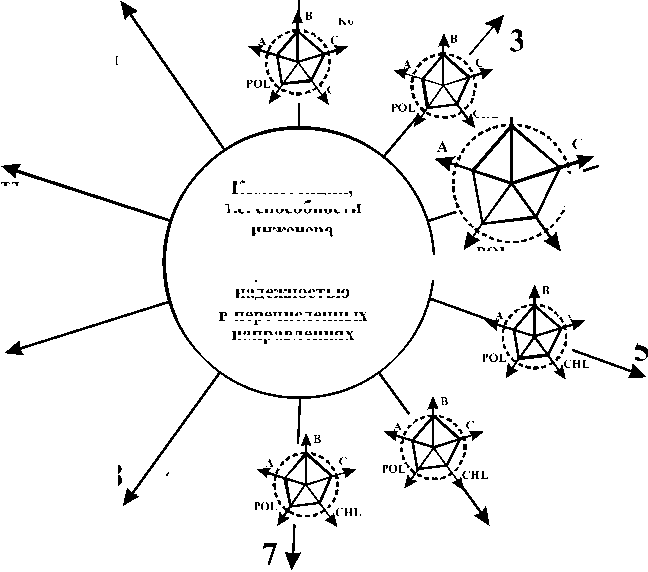
В целом, крайними вариантами компетентностного формата являются варианты неметрического компетентностного формата (НКМ) и метрического компетентностного формата (МКФ) (рис. 6).

Направление компетенции 2

Направление компетенции это направление свойства - способности инженера решать проблемы

Состояние    в этом направлении компетентности

отл хор удовл неуд

'С

Компетенции, т.е. способности надежностью в перечисленных направлениях

CHL отл хор удовл неуд отл хор удовл неуд

Компетенция -это организация в психике инженера

Компетентность как мера развитости инженера в этом направлении компетенции

Рис. 6. Разные варианты компетентностного формата (2-7 – метрический компетентностный формат; 1, 8-10 – неметрический компетентностный формат)

CHL

CHL

отл хор удовл неуд

инженера решать проблемы с определенной

POL

В результате, если построить конкретные техники вычисления величин A, B, C, POL, CHL, то будем иметь модель с метрическим компетентностным форматом.

Разумеется, чтобы деятельность инженера была бы эффективной, он должен руководствоваться определенной методологией.

Поэтому, в каждой области деятельности существует своя методология, как наука об организации, ведения, оценки результатов эффективности деятельности.

Освоенная инженером методология деятельности представляются в нем как личностные технологии (развитые способности) и приобретенные знания организации, ведения, оценки результатов своей деятельности, т.е. как компетенция в определенном направлении деятельности. Поэтому компетенция может быть определена как способность решать проблемы в определенном направлении деятельности.

Как следует из системного анализа деятельности инженера, проблемы бывают разной сложности, и чем сложнее проблема тем выше должны быть развиты способности, полнее и целостнее знания человека, который эти проблемы готов решить.

Для оценки сложности проблемы построим следующую цепочку рассуждений. Пусть некоторую проблему Х за предельно допустимое время работы Т может решить эксперт У со значениями показателей компетентности <А1, В1, С1, POL1, CHL1>. Следовательно, сложность проблемы Х можно оценить трудностью (трудоемкостью) ее решения экспертом У за время работы Т, т.е. сложность проблемы Х можно выразить через комплекс параметров <А1, В1, С1, POL1, CHL1, Т>.

Следует особо отметить, что Т – время исполнения одной единицы работы сложности <А1, В1, С1, POL1, CHL1>, т.е. производительность выполнения этой работы экспертом будет 1/Т (раб/час). Таким образом, в частности, можно говорить о производительности работы по формализации проблемы (работы типа А1); по конструированию решения проблемы (работы типа В1); по исполнению решения проблемы (работы типа С1), т.е. о величинах производительности работ 1/Т(А1) (раб/час), 1/Т(В1) (раб/час), 1/Т(С1) (раб/час) произведенные экспертом.

Очевидно. Чем выше уровень производительности труда в решении проблем, тем выше развиты АВС–способности и объемы знаний, поэтому значения метрик величин А, В, С можно взять

А = k—

T(A1)

В = k ——

T(В1)

С = k ——

T(С1)

(раб / час)

(раб / час)

(раб / час)

где k – безразмерный коэффициент масштабирования. Метрики величин POL и CHL, будем рассматривать в процентах освоения материла в рамках дисциплин.

Таким образом, каждая проблема (вернее ментальная модель проблемы – проблемная ситуация) имеет свою оценку сложности, т.е. является измеримым информационным объектом. В этом случае проблемы мы можем упорядочить по возрастанию сложности, взяв вектора системы компетентности за некоторую систему координат (рис. 7) и образовав тем самым метрическое проблемно-деятельностное образовательное пространство инженера (инженера-бакалавра, инженера-магистра).

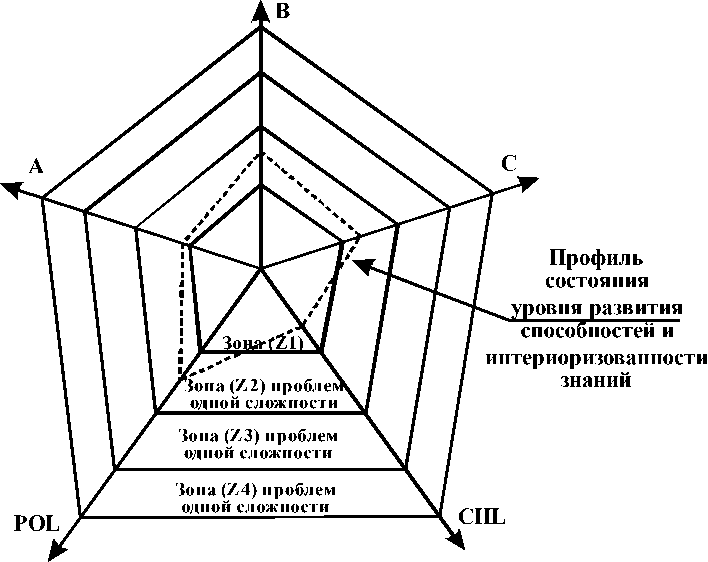
Рис. 7. Метрическое проблемно-деятельностное образовательное пространство инженера

Очевидно, при подготовке инженерных кадров (инженеров-бакалавров, инженеров-магистров) речь идет о формировании у них разных уровней развития АВС-способностей и интериоризованности знаний, т.е. магистры будут подготовлены к решению проблем из зон с более сложными проблемами.

Следовательно, за четыре года обучения можно сформировать один профиль уровня развития способностей и интеоризованности знаний (профиль инженера-бакалавра), а потом из лучших, добавив еще 2 года можно сформировать другой профиль (инженера-магистра). В результате, получается, что исходя из многих критериев, в России социально и экономически выгодно введение двухступенчатой образовательной системы [5, 6].

При проектировании дидактических систем бывает неясно сколько времени необходимо для освоения того или иного курса в рамках дисциплины. Чтобы это сделать построим следующую логическую последовательность.

Из модели развития Л.С. Выготского [7] следует, что на актуальный момент развития, человек способен решать проблемы с определенной надежностью не вше определенной сложности, т.е. на актуальный момент каждый имеет определенную зону своего развития. Освоение в развитии следующей зоны – «зоны ближайшего развития» позволит ему решать более сложные проблемы. Таков общий поступательный механизм развития способностей человека по решению проблем.

С дидактической целью в рамках модели Выготского введем некоторые параметры и их метрики. На рис. 8 изобржены зоны развития и зоны ближайшего развития в виде овалов, т.е. развитие будущего инженера происходит, начиная с зоны 1, через зону ближайшего развития (зона 2) и т.д. Разумеется, освоение зон ближайшего развития происходит за счет учебной деятельности по решению проблем. Причем, продолжительность времени освоения проблем (развитие способностей и интериоризации знаний) за счет учебной деятельности и сложность освоенных им проблем изменяется в разных масштабах. В целом, тенденция следующая: небольшие приращения сложности проблем при освоении требуют, как правило, больших приращений во времени. Например, на рис. 8 демонстрируется случай, когда небольшое приращение по сложности ∆ S требует для освоения большего приращения времени ∆ t.

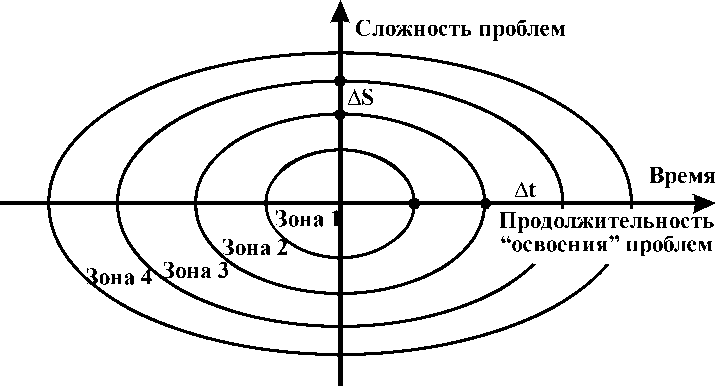
Рис. 8. Модель нелинейного изменения сложности проблем (приращение ∆ S) и времени их освоения (приращение ∆ t)

Приведем усредненные данные, требуемой продолжительности учебной деятельности для освоения обучаемым зоны ближайшего развития из зоны его развития. Усредненные данные получены в рамках учебной деятельности в рамках дисциплины «Моделирование систем» среди студентов четвертого курса, обучающихся по направлению «Информационные системы» в течении 4 лет (20042007 гг.).

Производительность решения проблем экспертом р (раб/час) – усредненные данные по учебному моделированию систем	Производительность учебной деятельности (лекции, практика, лабораторные работы) по научению решения проблемы с производительностью эксперта t (раб/час)
0	0
1	3
2	12
3	24
4	38

По этим данным можно построить аппроксимирующую функцию вида t=ap2

(p>0).

На рис. 9. приводится графическое представление этой функции. В аналитическом виде эта аппроксимирующая функция имеет вид t=2,73p2.

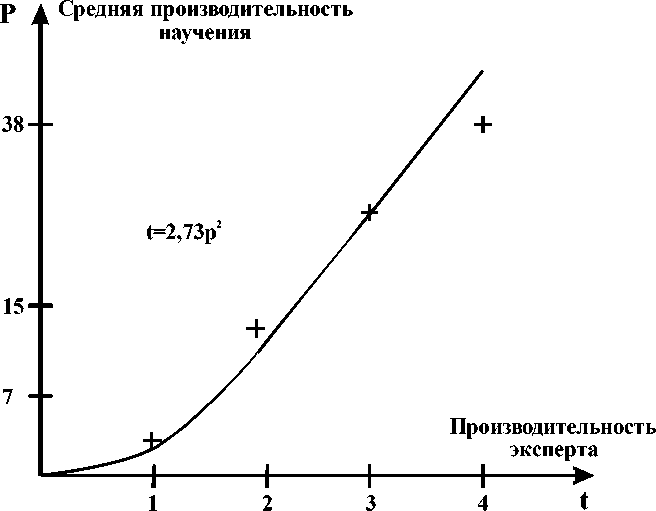
Рис. 9. Зависимость продолжительности перехода из зоны развития в зону ближайшего развития в рамках дисциплины «Моделирование систем»

Очевидно, что в рамках любой дисциплины, опираясь на экспериментальные данные можно вычислить аналогичную зависимость. Причем коэффициент 2,73 будет характеризовать сложность освоения дисциплины в целом, т.е. трудность освоения «Моделирование систем» характеризуется коэффициентом 2,73.

Таким образом, известную модель Выготского освоение «зоны ближайшего развития» сделаем метрической в рамках определенной дисциплины, т.е. если имеется учебная дисциплина, то по рассмотренной методике можно рассчитать среднюю продолжительность ее освоения будущим инженером.

Очевидно, если все профессионально ориентированные дисциплины будут излагаться в едином метрическом компетентностном формате, то на этом «поле» дисциплин гораздо легче сформировать единую инженерную компетенцию, достаточного уровня развития для решения сложных проблем современной инженерии.