Формирование математической грамотности учащихся с помощью практико-ориентированных задач

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 371.3.                                            

Глобализация, происходящая во всех сферах общества, оказывает непосредственное влияние и на образование: новые подходы к обновлению и достижение новых образовательных результатов, соответствующих современным запросам личности, общества и государства. На основе этого многие государства вынуждены пересмотреть свои устоявшиеся подходы к системе образования и такие же процессы происходят и в нашей республике. В направлении реформирования системы образования приняты важные документы, в частности, в 2021 году приняты «Стратегия развития образования в Кыргызской Республике на 2021-2040 годы» , в 2022 году утвержден Государственный образовательный стандарт школьного общего образования Кыргызской Республики .

Документы обусловливают необходимость ориентации системы образования на конечный результат, внесения изменения в процесс обучения с целью подготовки специалистов, соответствующих требованиям рынка труда. В настоящее время одним из основных направлений математического образования в школах является подготовка учащихся к использованию математики в повседневной жизни: умение применять математические знания на практике, умение глубоко мыслить и обосновывать ситуацию, развивать способность выбора подходящего из множества вариантов, умение доказывать свое видение. Все эти качества являются требованиями современного рынка труда. Этот аспект обусловлен возрастающим значением математики в системе общих знаний в последние десятилетия. С другой стороны, причина изменений в сфере образования Кыргызстана заключается в том, что обучение математике направлено на повышение личностных, творческих, развивающих качеств обучающихся. Именно идею формирования умений, навыков которые требуются для решения жизненных и реальных ситуациях у учащихся реализовывается в государственном стандарте образования. В этих условиях организация обучения строятся на основе анализа индивидуальных возможностей и интересов самих учеников. Другими словами, происходит уточнение ценностей современного школьного образования, ориентированного на конечный результат. Ориентированность на конечный результат обусловливает изучение состояния обучаемых, внесение коррекции в учебный процесс. В предметном стандарте по математике приведены учебные достижения по завершению изучения каждой главы. Однако следует отметить, что в школьных предметах по математике недостаточны задачи, нацеленные на формирование практических навыков, необходимых в повседневной жизни. Задачи и задания не направлены на развитие творческих, самостоятельных способностей ученика, в большинстве случаев они направлены на выполнение действий по образцу. В учебном процессе необходимо применять задания, направленные на развитие мыслительных операций. Задания, применяемые в международных сравнительных исследованиях PISA (Programme for International Student Assessment) и предполагающие применение знаний в жизни, направлены на выявление именно таких компетенций у ученика. Математические задачи PISA направлены на изучение способностей учащихся к анализу ситуации, доказательству и выражении математических идей, формулированию, решению и интерпретации математических проблем в различных ситуациях.

В основу организации области исследования математической грамотности положены три пересекающихся аспекта [2, с. 8]: математическое содержание, использующееся в заданиях; контекст, в котором представлена проблема; математические мыслительные процессы, которые описывают, что делает ученик, чтобы связать этот контекст с математикой, необходимой для решения поставленной проблемы. Результат исследования PISA 2009 года показал, что более 86,6% учащихся Кыргызстана не достигли минимального уровня математической грамотности . По заключению экспертов, «недостаточное владение знаниями по математике учащихся с низкими показателями может иметь для них негативные последствия в будущем при поиске работы и повлияет на их возможности полноценного участия в обществе» [6, с. 221].

Использование математических задач при обучении решает проблему применения полученных знаний на практике. Для этого учащимся необходимо пройти подготовку, так как только усвоение знаний не дает учащимся возможность применять их в различных ситуациях. Такой уровень подготовки достигается в процессе творческой и самостоятельной учебно-познавательной деятельности учащихся и раскрытия жизненного опыта. Эта способность формируется путем применения практико-ориентированных заданий в процессе обучения. Практико-ориентированные задачи – это задачи из окружающей действительности, которые тесно связаны с формированием практических навыков, необходимых в повседневной жизни [1, с. 72].

Цель — развить навыки, умения необходимые для работы в реальных ситуациях. Практико-ориентированные задания помогают учащимся работать с информацией, выделить и выбрать главное, принимать решение и их обосновывать, работать в группах и парах, отстаивать свои убеждения и идеи в поиске творческой деятельности.

Решение задач такого типа в большинстве случаев основано на построении математической модели реального состояния, описанного в задаче. Именно для подготовки модели требуется высокий уровень математической подготовки, и это результат обучения, которое называется общеобразовательным, общекультурным [2].

Систематическое использование практико-ориентированных задач на занятиях и активное применение математических знаний в повседневном жизни, дает учащимся уверенный взгляд на окружающий мир и способствует формированию и развитию математической грамотности учащихся. Важными отличительными особенностями практикоориентированных задач являются : значимость: познавательная, профессиональная, общекультурная, социальная, получаемого результата, что обеспечивает познавательную мотивацию учащегося; условие задачи сформулировано как сюжет, ситуация или проблема, для разрешения, которой необходимо использовать знания из разных разделов основного предмета – математики, из другого предмета или из жизни, на которые нет явного указания в тексте задачи; информация и данные в задаче могут быть представлены в различной форме: рисунок, таблица, схема, диаграмма, график и т.д.; указание (явное или неявное) области применения результата, полученного при решении задачи [7].

Нестандартный характер их структуры, т.е. неизвестность некоторых ее элементов, наличие разной степени рациональности, в частности, наличие множеств способов решения данной проблемы, иметь достаточно объемную формулировку условий при отсутствии недостаточных или избыточных данных является одной из особенностей практикоориентированных задач [5].

Как показывает практика, что технология обучения при использовании практикоориентированных заданий позволяет учащимся перейти от пассивного объекта педагогического процесса к активному субъекту образовательной деятельности. Необходимо также отметить, что использование задач, составленных в соответствии с местными и национальными особенностями является лучшим примером установления связи между математикой и жизнью [3].

Рассмотрим примеры практико-ориентированных задач для 6-х классов. В данных примерах моделируется реальная обстановка, выбирается оптимальный вариант решения задачи, имитируется его реализация в практической жизни, учащиеся могут установить параметры объекта и характеристики, которые позволят ему вычислять искомое число.

Прочитайте теист сарана.

АаЛапиг I,

Турист остановился в юрточтюм городке, чтобы переночевать. В той юрте он смажет переночевав, н шалеть одну порцию тииноналытого блюда «Бешбармак», один курут и 2 рала пылить кумыс по 05 литра, шиитш наименьшую сумму денег?

Выберите верный смиюи

В первой юрте

Во второй юрIC

Запишите ответ с обьягиеиием:

К )рточпме городка

Юрта одна из mmmcAiubx частей кыргыкнтй культуры. Юрт по переносное, каркасное, куполообразное жилите у киргизов На Иссык-Куле построены юрючныс городки, где часто туристы останавливаются н отлыхакл

Юрта 1
За ночлег	$00 сом (с ОДНОГО человека)
Бешбармак	720 сом 1 b.piUUTl
Куру»	30.5 сом ( за пиуку)
Кумыс	150 сом ( та пнтр)

Юрп1
За ночлег	400 сам (с одного человека)
Бешбармак	650 сом (порция)
Куру»	45,5 сом (ш штуку)
Кумыс	120 сом па литр)

Прочитаете thui. xia «тоета па вопрос восааяыувтесь с Таблицей расположенной справа.

ferMwitr 2

Кама нт них юрт обойдете» пой трутни туристов ламам?

Uкинине ответ < решением:

И>рточные городки

Юрта идти нт важнейших частей яырппской культуры Юрта сто переносное, каркасное, куполообрашое жилище у кмртыюп

На Иссык-Куле построены торточные городил, г ле часто туристы осганаазпааются н отдыхают

юрты < «ДИШ е ОДМСМ

Кя барна* (<»м>

КУЭРДак Кумыс

(опт)

М ЛШр (сои)

Юрта АН

МО

Акива

Юрта .42

проживает бсеткитмав

100     7 ЮО    7 4 50

Прочитайте текст справа.

ЬнМинеЛ

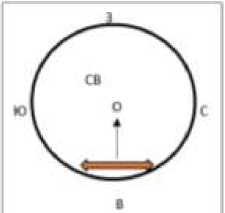
Чтобы асюгедшиЗт а юрту человек смотрел на север, на сколько

I рилу сов он лотами повернуты а'

выберите асе верные ответы:

a) W hi не

О IV dl 560*

Юрта

Юрта одна нт важнеПапп настав кыртынысо культуры Юреа по переносное, каркасное, куполопбраттюе жниште у шрсывтв Кыртыкхаа юрта устаиааптвалась так. чтобы анодная дверь acet да бы та рас сю х>жсна в ее восточной части, пики в юрту че товсь смотрит ■и мтид

Таким образом, использование практико-ориентированных задач для обучения математике в школе позволит обучающимся: создать практическую ситуации и включение учащихся в этот процесс; видеть и оценивать значение использования математического знания в их жизни; лучше освоить необходимый теоретический материал и применять полученные навыки на практике самостоятельно; закреплять и расширять теоретическое знание; проявлять самостоятельность и инициативу.