Формула первого регуляризованного следа для дифференциального оператора с разрывной весовой функцией

DOI:

Постановка задачи

Изучим спектральные свойства дифференциального оператора с разрывными коэффициентами, задаваемого на отрезке [0; п] дифференциальными уравнениями

1/iHx) + q ₁ (x)y ₁ (x) = Ла⁸^©), 0 6 х < X 1 , а >  0,               (1)

У(8)(х) + д2(х)у2(х) = ЛЬ8у2(х), х1 < х 6 п, b > 0,(2)

с условиями «сопряжения» в точке х ₁ разрыва коэффициентов

У ¹"^ ^{— 0)}   У^О^. + ⁰⁾

у1(х1 — 0) = у2(с1 + 0);        ат      =      ьт     , т = 12, ■ ■ ■,7, с граничными условиями у2т1)(0) = у1т2) (0) = • • • = у1т7) (0) =       ., = 0,(4)

т ₁ < т ₂ <  • • • < т ₇ ;    т ^ , п ₁ Е { 0,1, 2,..., 7 } ,    к = 1, 2,..., 7.

Предполагается, что коэффициенты дифференциальных уравнений (1), (2) удовлетворяют следующим условиям гладкости:

Q1 (х) ЕС 8 0:3|):   ^(х) ЕС 8 (х1; п].(5)

Уравнения (1), (2) можно записать в сокращенной векторной форме у28)(х) + Q(х)у(х) = Лр(х)у(х),   0 6 х 6 п,

У ^{( х )} =

ГУ 1 (х), 0 6х<Х 1 , [У 2 (х), Х 1 < х 6 п;

9 1 ^{( х )} , ^{5 ( х )} =

Ы^х) ,

а ⁸ , 0 6 х < х ₁ , b ⁸ , х ₁ < х 6 п;

0 6 х < х1, х1 < х 6 п.

р ^{( х )} =

параметр, функция 5(х) —

В уравнении (1)-(4) число Л (Л Е C) — спектральный

потенциал, функция р(х) — весовая функция, точка х1 Е (0, п) — точка разрыва коэффициентов. В случае отсутствия точки разрыва х1 (то есть когда Q Е С8[0, п]) диффе- ренциальный оператор был изучен в работе [13].

Изучение операторов с разрывными весовыми функциями было начато в работе [5]: рассмотрена сходимость разложений по собственным функциям в точках разрыва коэффициентов дифференциального оператора. Аналогичные вопросы для оператора четвертого порядка исследованы в [2]. В [9] автором рассмотрены спектральные свойства оператора второго порядка с кусочно-постоянной функцией. В работе [8] изучены операторы второго порядка с разрывными весовыми функциями, в том числе приведены примеры изоспектральных операторов (см. [15]). В настоящей работе мы продолжаем эти исследования: изучаем свойства оператора восьмого порядка с разрывной весовой функцией и вычисляем его регуляризованный след.

2.    Асимптотика решений дифференциальных уравнений (1), (2) при больших значениях спектрального параметра λ

Пусть Л = s ⁸ , s = ^Л, причем для корректности дальнейших выкладок зафиксируем ту ветвь арифметического корня восьмой степени, для которой ^Г = +1. Пусть ш _к (к = 1, 2,..., 8) — различные корни восьмой степени из единицы:

ш к = 1;

ш _к = е 28^{1 ( к} 1) , к = 1, 2,..., 8; Ш 1 = 1;

.           2П           2п\

Ш 2 = е 8 = cos I — I + г sin I — 1 =

--1-- г = z ;

2       2         ’

4пг

Ш 3 = е ⁸

= z ² = г;

...;

^Ш т ^z ,   ^Ш п +8    ^Ш т ,   ^т   1, ² , . . . , ^8;

ш ₄ =

Ш б =

-

—к

2 ^;

Ш 7 =

- ^{г ;}

^Ш 8 = Т

-

+ 72 г;

⁺ 2 ^;

V2

-----г.

Ш 5 =

- 1;

Для чисел ш _к (к = 1,2,... 8) из (6) справедливы следующие свойства:

^ Шт = 0,  т = 1, 2,..., 7;  ^ Шт = 8; т = 0, т = 8;(7)

к=1

^ ^ш т = ^{0 ,    т} = ^{2 , 3} ,...,8;   ^ ^ш т = ^{8 , т} = 1.

к=0

Аналогично монографии [12, гл. 2] устанавливается следующее утверждение.

Теорема 1. Общее решение дифференциальных уравнений (1) , (2) представляется в виде

У1(ж,s) = ^С1кУ1к (ж, s);   ^(т)(ж, s) = ^С1к^(т)(ж, s), т = 1, 2,..., 7;(9)

к=1

Ыж, s) = ^^2кУ2к (x,s);  у2т (x,s) = ^С2,к: у^ )(^,s),  т = 1 ^..^ 7;

к=1

при этом С _{1 к} ,С _{2 к} (к = 1,2,...,8) —произвольные постоянные, причем для фундаментальных систем решений { у _{1 к} (ж, s) } ⁸ ₌₁ и { у _{2 к} (ж,з) } ⁸ ₌₁ при s ^ то справедливы следующие асимптотические формулы и оценки:

У1к (ж,s) = е“Ш^[1+ Шк ^(ж) + ^s^ + о^ ^^ ^], к = 1, 2,..., 8,(11)

^)(<=,^) = (а"б         1 + "ЛМ + к-/' . О^) ,(12)

к = 1, 2,..., 8; т = 1, 2,..., 7;

№6 (+,s) = е1" “'1 + "УгА + 508/2+ о( ^^), к =1,2,..., 8;(13)

//<■”)(+,s) = (6" .    " [1 + "фМ + в + 2(      )],(14)

к = 1, 2,..., 8; т = 1, 2,..., 7;

1 Г

^Л 7 ^{( / )} = ^-_Q 7     q 1 ⁽ t ⁾ dt^{,   Л} 7 ⁽⁰⁾ = 0;

^8а' Jq

Л 8 (/)

ЛтМ

1   Г'

В 7 (/) = - 8^ 7     92^М,  5 7 (/ 1 ) = 0;

⁷ , 1 ^{( / )} - ⁷ ^ i ⁽⁰⁾       i _ 5^ 1 ^{( / ) -} 7g i ⁽⁰⁾

16а ⁸        ’                     16а ^{8        ;}

(7 - 2т)д х (ж) - 7, 1 (0)

16а ⁷

, т = 0,1, 2,..., 7;

л 7 (г) =

⁵ 7 ^{( / )} =

, 1М 8а ^{7 ;} 9 2 ^{( / )} 86 7 ^;

^Л 8 ^{( / )}

Л^) =

3g i (/) - 7, 1 (0) _

16а ⁸

- 7g i (/) - 7, 1 (0) _

16а ^{8         ;}

.;

, а/ X _ ⁷ , 2 ^{( ж ) - 7} , 2 ⁽ Х 1 )       1     _ ⁵ 9 2 ^{( / ) -} 7, 2 ⁽ Ж 1 ⁾

'8 в"             1668        ’ В в"             1668

• - ^2т)9^ - ^{7, 2 ($ 1 )} , т = 0,1,2,. ..,7;

)6( А _ ^{- 5} 9 2 ^{(ж) - 7} 9 2 ^{( /} 1 )    _Д7/ х _ ^-7 ? 2 ^{( / ) - 7} 9 2 ^{( /} 1 )

8 (Ж)=         1668        ;   58 (Ж)=166

Для коэффициентов асимптотических формул (11)–(18) справедливы следующие соотношения:

^Ь Л№) = ^Ъ л?(0) = ^Ъ л?(/1) = »8 = -^Л?);(19)

т=0        т=0т=0

Ъ втм = Ъ втао = £ 5т(п) = ^ = - 7^2Л2.(2с> т=0        т=0

Для фундаментальных систем решений { « _{1 6} (/, s) } ⁸ =1 и { « _{2 6} (/, s) } ⁸ =1 из (11)-(14)

справедливы начальные условия:

Л 7 (0) = 0; Л 8 (0) = 0;  5 7 (^ 1 ) = 0;  В ?^ ) = 0;

« 1 6 (0,s) = 1;   « 2 6 (X 1 ,s) = е ^ь " * ⁵ ' 1 ;

_У - ^т ) (0,₅) = «_{1 Ш ь} ,) - [ ! + 1 +        .     1)] ;

« ⁽ т ) (/ 1 ,») = (6" t 8) ^т е ¹ " * “1 1 + 5 + ^В + о ( ;2 ; ) ,           (21)

к = 1, 2,..., 8; т = 1, 2,..., 7.

3.    Изучение определителя Вронского A02,2(x, s)

Пусть A 02,2 (x,s) — определитель Вронского фундаментальной системы решений {y _{2 k} (x,s) } | =1 дифференциального уравнения (2)

A o2,2 (x,s) = detWr[y 21 (x, s),y 22 (x, s),...,y 28 (x,s)] =

У 21 (x, s)    y 22 (x,s)   ...  У 27 (х, s)    y 28 (x, s)

У 21 ^{( x,s )}    У 2 2 ^{( x,s )}    . ..  У 2 8 ^{( x,s )}    У 2 8 ^{( x,s )}

............................ y 2 ⁷ i ^{) ( x,s )}   у 2 ⁷2 ^{( x,s )}   ...  y 28 ^{) ( x,s )}   y 278 ^{( x,s})

Из общей теории линейных дифференциальных уравнений известно, что определитель Вронского A ₀₂ , ₂ (x, s) не должен зависеть от x: ^A 02 , 2 ^{( x}, ^{s )} = ^A 02 , 2 ^{( s )} = °.

Применяя формулы (13)–(18), имеем

Ao2,2(x, s) = h1 [1 + ^1^Mx>+ S! + ...]      ... h8 [1 + ^8-|7Cx)+ 3 .

Wv [ 1 + -   ■ , s + ... ] ... ^w [ 1 + Ц^ S +... ^] ,

„„(^ ^[1 + “'      ' + S ₊ ...^] ... „ .   ,, ^[1 ₊ ^v'' ₊ S ₊ ...^]

где введены обозначения h ^ = е ^{Ьш к sx} , к = 1, 2,..., 8.

Обозначим через A ₀₀ определитель Вандермонда чисел ш 1 , ш ₂ , ..., ш ₈

A ₀₀ = det Wandermound ‘ s(^ 1 , w ₂ , ..., ш ₈ ) =

1     1     1    ...1

Ш1  Ш2  W3  ...ш

2      2      22

П ( V - _{Ш т} )=A oo = 0. /с>т;

к,т=1 ,2,...,8

Ш1  ш2  ш3  . . .Ш

.............. ,..7 ,..7 ,..7,..7

iv 1 ш 7 ш 7 ... ^ 8

Справедливо следующее утверждение.

Лемма 1. Пусть ( Ь _тк ) (к,т = 1,2,..., 8) — матрица алгебраических миноров к элементам Ь _тк определителя A 00 из (24) . Тогда

/би   812   ...§

⁽⁸ тк )

521   §22   . . .§

...........

§81   §82   . . .§

		1	- 1	1	- 1     . .	.1	— 1
		- ω 1 - 1	ω 2 - 1	- ω 3 - 1	W - 1    .	. — W 7 -	ω 8 - 1
= A oo - 8		ω 1 - 2	- ω 2 - 2	-2 ω 3-2	— W 4 2 .	-2 . W 7	- ω 8 - 2	.            (25)
	⎝	ω 1 - 6	- ω 2 - 6	ω 3 - 6	- W 4 - 6 . .	. W 7 6	- ω 8 - 6
		- ω 1 - 7	ω 2 - 7	- ω 3 - 7	W 4 - 7     . .	. — W 7 - 7	ω 8 - 7

Доказательство леммы 1 можно найти в работе [7]. Для вычисления определителя А ₀₂ , ₂ ( ж, s ) из (23) вынесем из к-го столбца (к = 1, 2,..., 8) множитель h _k , из к-й строки вынесем множитель (bs) ^{k- 1} и разложим получившийся определитель по столбцам на сумму определителей. В результате получаем

Ao2,2(^,s) = н8 Л                      ^[л i A02,2,7(ж,s) , A02,2,8(ж,s) . n / 1 41       (26)

= Пк=1 ^hk ^{( bs )( bs ) 2 (} ... K^y ^A 00 +---- S7----⁺----S 8---- ⁺ °UJ ,

^А 02 , 2 , 7 ^{( ж}, ^s) = ^W 1 ^B 7 ⁽ Ж ^)А оо + Ш 2 ^В 7 ^(ж)А 00 + • • • + Ш 8 ^В 7 ^(ж)А оо = = ^A 00 ^B 7 ^{( ж )(w} 1 + ^w 2 + • • • + W g ) = ^A 00 ^B 7 (ж) • 0 = 0;

^А 02 , 2 , 8 ^{( ж}, ^s) =

В 0 (ж) ы^^ж)

ω 2

.

.

.

.

.

.

ω 8

+

ω 1

^В 0 ^{( ж )     1}

.

.

.

Ш 2 В 8 ( ж) W 3 .

.

.

ω 8

+

ш 1 В 7 (ж) ш 7 ... W 7

W 7 ш 2 В 7 (ж)

+ • • • = ^{[ B} 0 ^{( ж )} Su ^—

^W 1 ^B 8 ^(ж) ^ 21 + ш 1 ^В 2 ^{( ж )} 5 з1 ^— • • •

-

7            7

w 7 ... W 7

w 7 B 7 (x)5 g1 ] +

⁺ [ ^{— В} ° ^(ж) 5 12 + Ш 2 ^В <^{1 (} Х ⁾ 5 22

-

^W 2 ^B 8 ^(жЖ з + • • • + ^w ₂ ^B 8 ^(x) ^ 82 ^] + • • • =

= A °° • 8 i>k (ж) = A oo S g . ⁸     k=8

Учитывая, что H k =₁ h k = П к ₌₁

_еь _{Ш к 8}х = _еь⁽ _ш1^_ш2⁺.^_ш^х = _е 0 = 1, получаем

A o2 , 2 (ж, s ) ⁽²⁶⁾ = ⁽²⁸⁾ (bs) ²⁸ A oo 1 + S 7 +    + о (J 9) ,               (29)

то есть определитель А ₀₂ , ₂ (ж, s ) = A ₀₂ , ₂ ( s ) не зависит от ж, что подтверждает справедливость вышеописанных асимптотических формул (13)–(18).

Аналогичным образом доказывается, что определитель Вронского А ₀2 , ₁ (ж, s ) фундаментальной системы решений { ^ _{2 k} (ж, s ) }⁸ =₁ дифференциального уравнения (1) также не зависит от ж, и для него справедлива формула

А о2 , 1 ( ж, s)=det Wr[^_n(ж, s ); У 12 (ж, s ); ...; -у^ж, s ) = (as) ²⁸ A oo

1+4+4 8 +о s ⁷     s ⁸

-Ш

D 8 (1 =

_ 7^ 1 (0) 2a ⁸

4.    Изучение условий «сопряжения» (3)

Применяя формулы (9), (10), из условий «сопряжения» (3) получаем

У 2 (^ 1 + 0, s) = У 1 (Х 1

-

0, s) О ^2 C 2k У 2k (X 1 + 0, s) = ^ C 1k У^ (^Ж 1

- 0,s);      (30)

k=1

У2т)(^1 + 0, s) (3)У(т)(ж1 - 0,s) (bs)m     ”     (as)m т = 1, 2,..., 7.

" ^k k =1

k =1 у 2 " ⁾ (^ 1 + ^{0 ,s})

(bs) ^m

= E C 1 k k =1

(.^{( m )}^

^у 1 k ^{( Ж} 1 ^-

(as) ^m

0,s)

,

Рассматривая систему (30), (31) как систему из восьми уравнений с восемью неизвестными C21, C22,..., C28 (при этом Сц, C12,..., C18 — параметры), приходим к выводу, что эта система имеет единственное решение r< = A21    ■      =  A22  ■   ■    =  A2k     ^=19 Я

^С21      *      / \ / n;    ^ 22 a / \ ; . . . ; ^ 2k *       / \ , ^к 1, ² , ... , ⁸ ,

^A 02 , 2 ^{( s )} = ^{0            A} 02 , 2 ^{( s )               A} 02 , 2 ^{( s )}

при этом определитель A _{2 k} (к = 1, 2,..., 8) получается из определителя A ₀₂ , ₂ (s) ной к-го столбца на столбец

( У2 ^C 1 k У 1 k ^{( ж} 1 ^{— 0}, ^{s )} ; k =1

Е^

k =1

У 1 k ^{( х} 1 - ^{0 ,s )}

as

; . . . ;

У^ ^{( х} 1

-

(as) ⁷

М у.

заме-

Таким образом, имеем

△ 21

A 22 =

E ^с 1к У 1к (^ 1

k =1

E^1k k=1

5 82 c 1k k =1

-

У 1 к (^ 1

-

as

^у 1 k '^z ।

-

0,s)

0,s)

У 22 (^ 1

У 2 2 ^(ж 1

⁺ 0, ^{s )}

⁺ 0, ^{s )}

bs

0,s) у 22 ) (х 1 + 0,s)

(as) ⁷

(bs) ⁷

. . .    У 28 (^ 1

у 2 8 ^{( ж} 1

...

.

.

.

⁺ 0, ^{s )}

⁺ 0, ^{s )}

bs

у 2з ^{) (ж} 1 + ^{0 ,s )} (bs) ⁷

= ^С 11 ^A 211 ^{+ C} 12 ^A 212 ⁺ • • • ^{+ C} 18 ^A 218 = ^2 ^C 1 k ^A 21 k 5

k =1

У 21 ⁽ Ж + ^{0 ,s )}

У 21 ⁽ ^ 1 ^{+ 0 ,s )} bs

E C 1 k У 1 k (^ 1 - 0, s)   У 2з (Ж 1 + 0, s)   . .. У 28 (^ 1 + 0, s)

k =1

у 1 k ⁽ ^ 1 ^{- 0 ,s )}    у 2з Оа ^{+ 0 ,s )}         у 28 ^(ж 1 ^{+ 0 ,s )}

2-/ c1k                                      ,                . . .              , k=1          as              bs                   bs

у 21 ^{) (} ^ 1 + ⁰ , ^{s )}    28, _r у 12 ⁽ ^ 1 ^{- 0 ,s )}    у 23 ^{) (} ^ 1 ^{+ 0 ,s )}         у 2з ^{) (ж} 1 ^{+ 0 ,s )}

(bs) ⁷         k =1 ^{1 k}       (as) ⁷               (bs) ⁷         ...         (bs) ⁷

= ^C 11 ^A 221 ^{+ C} 12 ^A 222 ⁺ " " " ^{+ C} 18 ^A 228

= Z^C 1 k A 22k ;.

;

k =1

Л 2 т = С 11 Л 2т1 + С 12 Л 2т2 +	• • • + С 18 Л 2 т 8 = У2 С 1к Л 2тк ,   ^ = 1, 2 , . . . , 8 к =1	(34)
Л 21 к = У 21      У 1к у 2 1      у 1 к	У 1к      У 22     ... У 28 У 1к      У 2 2            У 2 8 as      bs           bs        . (7)          (7)                   (7) У 1к     у 22          у 2% (as) 7    (bs) 7    ... (bs) 7 Ж 1 ± о У 23      . . . У 28 У 2 3            У 2 8
л _ bs    as Л 22 к = ......... (7)         (7) ^ 21      У 1к (bs) 7    (as) 7	bs             bs         ;...; к = 1,2,..., 8. у 2?         у )? (bs) 7 ... (bs) 7 Ж 1 ± о	(35)

Применяя формулы (11)-(18), вычисляя определитель Л ₂₁₁ из (33)-(35) аналогично определителю Л ₀₂ , ₂ (ж, s) из (23)-(29), получаем

^{+ [ —} В ° ⁽ Ж 1 ⁾⁵ 18 + ^Ш 8 ^В 8 ⁽ Ж 1 ⁾⁵ 28 ^— Ш 2 В 2 ⁽ Ж 1 ⁾⁵ 38 + • • • + ш 8 В 7 ⁽ Ж 1 ⁾⁵ 88 ^{] —}

(25) Л 00                Л 00

=  8 ^^8 ^^ ⁽ ^ 1 ^{) +} ••• ⁺

, ^Л00 \ пк(   \ (19),(20) ^Л 00

+ -|-2_,^В 8 №)  =    ₈ ^(/Л + 7^ 8 ).                    ⁽³⁷⁾

Таким образом, имеем

Л 211 = Л со е^ ¹-^¹ 1 + "''/"■ ^ 8 +7^ 8 + О (1) ; (38) для нахождения определителя Л ₂₁₂ из (33)-(35) вычтем из первого столбца второй и разложим по первому столбцу

Л

_ OW15Ж1

X

X

1 •

"      Ш 1 Л г (ж 1 ) +     s 7

+

л 0 ( ^ 1 ) s 8

+.

..

... 1 •

1+

0 s 7

+

В 0 ( Ж 1 ) s 8    +

..

Ш 1

" 1 + Ш 1 Л 7 (ж 1 ) s 7

+

л 8 ( ж 1 ) s 8

+.

. . . Ш ?

" 1+

0 s 7

+

B ? 1^ 1 ) s 8    +

.. ]

ш 7

"     Ш 1 Л г (ж 1 ) +     s 7

+

Л 7 ( Ж 1 ) s 8

+.

..

. . . Ш ?

1+

0 s 7

+

B ? 1^ 1 ) s 8    +

..

(7) = 24) е ( аШ 1 -

Ъ ш 1 ) s£ i

Л оо +

ω 1

Л 7 ( ^ 1 )Л оо s 7

Л 211 , 8 1       s 8

+o ( i )]

,

(7),(24)

^Л 211 , 8    —   ^[Л 8 ^{( ж} 1 ⁾⁵ 11 ^{— Ш} 1 ^Л 8 ^{( ж} 1 ⁾⁵ 21 + ш 1 Л 2 (Ж 1 )5 з1 -•••- W^ 7 (^ 1 )5 81 ] +

^{+ [—} В ° ⁽ Х 1 ⁾ 5 12 + Ш 2 В 8 ⁽ Ж 1 ⁾⁵ 22 — ^{ш 2 В} 2 ^{( ж} 1 ⁾⁵ 32 + • • • + ^{ш 7 в} 7 ⁽ Х 1 ) 5 ?2 ^] + • • • +

__ „а,Ш 2 5Ж 1 ^Ь ш 2 5Ж 1

212 — ^е е

(... )е ^Ьш 8 ^8Ж 1

X

X

1 • Го+ WAA s ⁷

Г    Ш 2 Л ₇ (Ж 1 )

^w 2 [¹⁺ .

^A 8 ^{( x} 1 ) - вОЫ

⁺        s ⁸

^A 8 ^{( x} 1 ) - ^Ы

⁺        s ⁸

+1 • 1 +

+ . . . ] . . . W8 [1 +

Б 8 (ж 1 ) s ⁸

^B 8 ^{( x}i) s ⁸

+ . . .

+ . . . ]

(7),(24)

ω 7₁

шАтЫ   Л ^{7 (} Ж 1 ^{) — B} 7 (^x 1 )

s ^{7     +}        s ^{8        +}

(7 — 24) _e ( «W 2 -_b W 2 ) _S$i ^ + ^W 2 ^ 7 ^{( x} 1 ) " ⁰

+

^w 7 1 +

△ 212 , 8 s ⁸

BK^ , s ^{8    +} ...

+o(B 1,

△ 212 , 8 ^{— (} A ° ^{( x} 1 ) ^{— b 0 ( х} 1 ))6 11 — Ш 2 ⁽ A 8 ⁽ X 1 ) — ^B 8 (^x 1 ⁾⁾ 5 21 ⁺ ш 2 ⁽ Л 2 ⁽: Г 1 ⁾ — В 2 ⁽ Ж 1 B& 31 — • • • —

• - w 7 (A 7 (X 1 ) — B 7 (X 1 ))5 ₈1 — △ 00 £ A 8 Ц ^W У — △ 00 £ B k (X 1 )( ^W У ⁽¹⁷ — ¹⁸⁾

• 8 k=0       VW1V

(17—18) £ нЬ8 [(—7^1(0) E W" + »Ы EP — 2-") /W2)"] — m=0

8^ ha [(—7)q2(x1) E w" + 92(x1) E(7—2m)(wf) ] — m=0            m=0

• — — △^ Ag(x1), H2 — 1 + (1 + V2)z,(40)

так как ^ " =₀ w " — 0, где введено обозначение △ ( j (x ₁ ) — S 2 ( 2; i ±⁰ — ^{9 1 (:}, ¹ ₈ ^-0) — так называемый «обобщенный скачок» потенциала q(x) в точке разрыва x ₁ .

Аналогично определителю △ ₂₁₂ из (39), (40) вычисляются определители △ ₂₁ ^ (к — — 3,4,..., 8) из (33)-(35): из первого столбца определителя вычитаем к-й столбец, получившийся определитель раскладываем по первому столбцу, в результате получаем:

• △21^ — е^1^-bwi)sx1 [0 + wA7(X1L2 + △21Е8 + о(    1, к — 2, 3,..., 8,(41)

s7              s8

Д      △ оо ^E дт/ х/ ^w k )     △ 00 ^E_дт/ х/ ^w k )

△216,8——.Msto) (^W1J — — 2_,Bs(x1) (^W1J —--16—A»(x1), к — 2,3,...,8; Нк —    £ i—2-/W6)";(42)

8 n 8\Wi/ m=0

H 2 — 1 + (1 + V2)z; H 3 — 1 + г; H 4 — 1 — (1 — V2 z); H 5 — 1;

Н б — 1 + (1 — V 2)z — TH 4 ; H 7 — 1 — г — TH 3 ; H 8 — 1 — (1 + V 2)z — TH ₂ ;

H10-k — THк,   к — 2, 3,..., 8.(43)

Аналогично формулам (36)-(43) изучаются определители А _{2 тк} (т, к = 1, 2,..., 8) из (33)–(35), в результате чего приходим к выводу, что справедливо следующее утверждение.

Теорема 2. Матрица определителей А _{2 тк} (т, к = 1,2,..., 8) из (32)-(35) , возникающая при изучении условий «сопряжения» (3) , обладает следующими свойствами:

А 2кк = А оо е ^{( аШ к} [ 1 + ^{Ш к Л 7} ₇ ^{(Ж 1 )} + ° ⁸ + ^8 + о( -¹) 1,   к = 1, 2,..., 8;

_         s'           8s ⁸          М

И

^А 21 ™ = Аое^ ™ ^- "^ [° + ₇ - 5 8 + о(_?)] , т = ² , 3,... ,8;

И

^А 221 = А о            ⁰ + - - 16S L + ₂(-) ;

И

А ₂₂ т = А - •'    ■•'

А _{2 к}т = А - ■' ~ ^Ъш^ [о + 0

0 + — —И; ^ ' Of "^ , т = 3,4, •••,8;

s'     16s8

И т.\  + of^)!, к = т, к,т = 1,2,..., 8;

16s8

Нп±8 = нп, п = 1, 2,..., 8; Нп = HnAq(xi),(47)

величины Н _п (п = 2,3,..., 8) определены формулой (43) ,

\    9 2 (^ 1 + ⁰⁾

^А9Ы = -- ^8--

-

9 1 (^ 1 - 0) а ⁸

^ i^{mp) (0} ,^{s )} (4) 0 . \ '^ ^ (as) ^mp                   "

х 7                 к=1

. \ С1кш'к?1’ [1 + — + к=1

1 к                     0.-

(as) ^m p

л т^р< s ⁸

(^оШ ]=0,

р = 1, 2,..., 7.

Из последнего из граничных условий (4) с помощью формул (10)–(14) и (32)–(34) имеем

^^{ni ) ( n,s )} (4)   „Х^р  ^ 2 fc ^{1 ) ( n,s )}

= 0 .

■         . АС2‘

( 7 1 )^

. Е Е °1-А2к„ ^2^^ = 0. Е С1кФЙ (п, s) = 0, к=1 ^п=1          /   ( )

8^         ?/^(п1)

Ф1к (n,s) = Е А 2 пк ^{Е 2} тг( пг² , к = 1, 2,..., 8.

п=1

Однородная система (48), (49) из восьми линейных уравнений с восемью неизвестными С 11 , С ₁₂ , ..., С ₁₈ имеет ненулевые решения только в том случае, когда ее определитель равен нулю. Поэтому справедливо следующее утверждение.

Теорема 3. Уравнение на собственные значения дифференциального оператора (1)– (5) имеет следующий вид:

/ О- П ^ 0 +

Ь 11 = ш ' ¹

Ь 21 = ш ' ²

Ь12 = ш'1    ...    Ь17 = ш'1      Ь18 =ш

Ь22 = ш'2    ...    Ь27 = ш'2      Ь28 =ш

X

Ь₇ 1 = ш ' ⁷       6 72 = ш ' ⁷

Ь 77 = ш          Ь 78 = ш ' ⁷

= 0.

Ь 81 = Фп (п, s) Ь 82 = ф^ (п, s) .

. Ь 87 = ф 1 7 (п, S) Ь 88 = ф^ (п, S)

Раскладывая определитель /(s) из (50) по последней строчке, получаем:

/ ^{( s )} = ^{Ф 1} 1 ^(п , ^{s )} ^ 81 - ^ф 1 2 ^(п , ^{s )ф} 82 + ^ф 1 3 ^(п , ^{s )ф} 83 ----- +

+ Ф 1 7 (п, s) ^ф 87 - Ф 18 (п, s) ^ф 88 = 0,                          (51)

^ф 88 =

ш ' ¹   ш ' ¹

ш ' ² ш ' ²

ш ' ¹      1 ' ¹   г ' ¹

ш ' ² ( = ) 1 ' ²   г ' ²

г б ' 1

г б ' 2

ш ' ⁷ ш ' ⁷

ш ' ⁷

1 ' 7   г ' 7

г б ' 7

= det Wandermound ‘ s(г ^{Ш 1} , г ^ш 2 ,..., г ^ш 7 ) = П    (г ' — г ' ^п ) = 0.

/с>п к,п=1,2,...,7

^ф 81 =

ш ' ¹

ш ' ²

ш ' ¹

ш ' ²

ш ' ¹     г ' 1

ш ' ² ( = ) г ' ²

г 2 ' 1

г 2 ' 2

г 7 ' 1

г 7 ' 2

= г ^м 7 ^ф 88 ,

ш ' ⁷ ш ' ⁷

ω

' 7 8

г ' 7   г 2 ' 7

г 7 ' 7

М 7 = ^ Ш 7 ; (53) /г=1

^ф 82 = г ^{2 М} 7 ^ф 88 ; ^ф 83 = г ^{3 м} 7 ^ф 88 ; • ••; ^ф 8 /= = г^{км? ф} 88 ,    к = 1, 2,..., 8.      (54)

Подставим формулы (52)-(54) в (51), поделим на г ^м 7 ^ф ₈₈ = 0, получим

/(s) = Ф п ¹ (п, s) — ф^ ¹ (п, s)г ^{M 7} + ф 1 3 (п, s')г ^{2 М} 7 -----ф ” 8 (п, s')г ^{7 М} 7 = 0,      (55)

где функции фЦ(п, s) (к = 1, 2,..., 8) определены формулами (49), (44)-(47), (13)-(18).

Для нахождения корней уравнения (55) необходимо изучить индикаторную диаграмму этого уравнения, то есть выпуклую оболочку показателей экспонент, входящих в это уравнение (см. [1, гл. 12]). Индикаторная диаграмма уравнения (55) представлена на рисунке 1.

Из общей теории нахождения корней квазимногочленов вида (55) (см. [1, гл. 12]) следует, что для нахождения корней уравнения (55) в секторе 1) в этом уравнении необходимо оставить экспоненты с показателями Мш ₈ = Мш ₂ и Мш 1 = Мш 1 (остальные экспоненты — бесконечно малые величины, их можно отбросить), в секторе 2) необходимо оставить экспоненты с показателями Мш ₈ = Мш ₂ и Мш ₇ = Мш ₃ , в секторе 3) — экспоненты с показателями Мш ₇ = Мш ₃ и Мш ₆ = Мш ₄ и т. д.

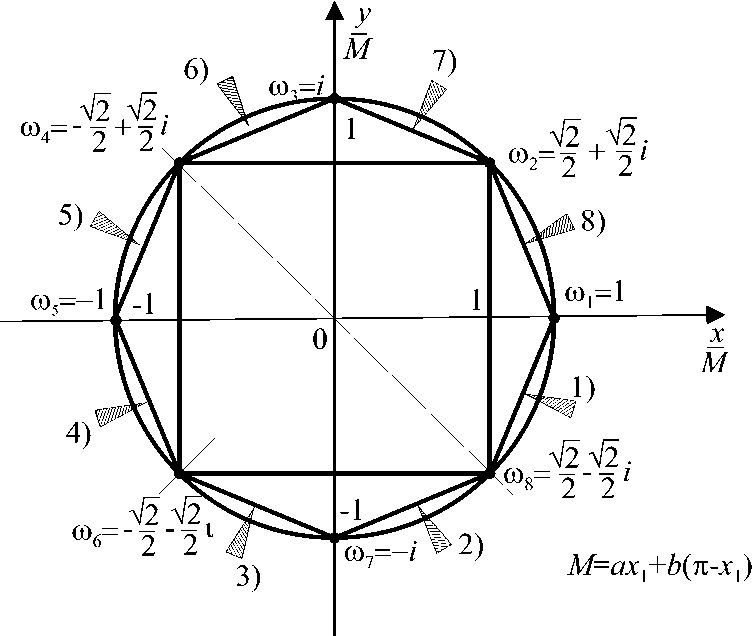
Рис. 1. Индикаторная диаграмма уравнения (55)

6.    Асимптотика собственных значений дифференциального оператора (1)–(5) в секторе 1) индикаторной диаграммы (рис. 1)

Из вышесказанного следует, что справедливо следующее утверждение.

Теорема 4. Уравнение на собственные значения дифференциального оператора (1)– (5) в секторе 1) индикаторной диаграммы (56) имеет следующий вид:

Ms) = Ф 1 1 (n, s) - ф ” 2 (n, s)M 7 = 0.

Подставляя в уравнение (56) формулы (49), (13)–(18), (44)–(47), приведем его к следующему виду:

»м =;„■. _е« - [i+^м+^s i ¹ +₂(S9) ]₊

। _е ( аШ 1 - Ьш 2 ) sx i

_m n. b a^ ( - H^z i ) ^ ⁶          16s 8

} - V^м ^ш2 е ^мш 2 ⁸

Ш 2 ^ 7  ^£

⁺ s ^{7 +} s ⁸

+<й]

+

। _е ( аШ 2 - Ьш 1 ) 5Ж 1

п 1 Ь ш 1 8 п ⁽ H-^Aq^C ¹ )

^Ш 1 ⁶          16S 8

= 0;

^ 7 = ^ 7 (C 1 ) + В 7 ( п ); ^ ” 1 = ^D 8 ^{+ 7 Е 8} + В !^ ¹ (п); H - = 1(1 + V 2)z; H i = H - .

Поделив в уравнении (57) на ш ” ¹ е ^Мш 2 ⁸ = 0, перепишем его в более удобном виде:

h i (s) = е ^{м ( W 1 —W} 2 ^{) s} [1 +

ω 1 ψ 7

S ⁷

+f+ош ]—

—

,М 7 А

^Z  ш ” ¹

ω 2 ψ 7

S ⁷

+f+о(к) ]+

^{A q (}_ ^{X1 )} [^ш2 ( аш 1 — Ьш 2 ) 8Х 1 ^W 2 sn^—Нш 2 5/^- и

'1.x  ш ^{1 е        е е     (— H 8 ) —}

—

z M 7 е ( а.ш 2 - ьш 1 ) 5Ж 1 е &ш 1 5П е - м W 2 S ( _— ^^ )] + о^ ¹ ^ = о

2пг

Основное приближение уравнения (58) имеет вид (ш 1 = 1, ш ₂ = z = е 8 )

П 1                                                            т

М ( W 1 - W 4 ) S _ М 7 ^ш 2 _ 2^7 2^ 2 пгк        _     ^{2п гк}

е         = Z Ш”1 = е е е ^ ^-    = М(Ш1 — Ш2) , к = к +

М ₇ + п 1

, к Е N.

Теорема 5. Асимптотика собственных значений дифференциального оператора (1)– (5) в секторе 1) имеет следующий вид:

2пг      ~   А 7 к 1 ^ 8к 1      f 1 А Т        М 7 + И 1

sк i = тт?--------- ? к +    , +—=7-,- + О( — ) , к = к +--, к Е N. (60)

к,1   М(Ш1 — Ш2)[ Т7     к8    ”U9y Г              8   ,

Доказательство. Применяя формулы Тейлора, имеем ем(ш1-ш2^1 (=) ехр [м (Ш1 — Ш2 )sM,m2^ (к + ЕЕ + ■ ■ ■)’ =

= zM7 z” [1 + 2П^А7к^ + 2п^А8к^ + of £ К(61)

L      к ⁷        к ⁸ \к⁹Л

М^^ f1 — АткД +of )).(62)

(2пг)7 к7            к8

Подставляя формулы (60)–(62) в уравнение (58), учитывая формулу (59), получаем z М7 z”1

1+

2лг^ 7 к, 1 к ⁷

+ № +о( Л 1х к⁸         к к⁹

х

[ 1 + ^ш 1 ^ 7 ^{М 7 (ш}1^— m2⁷ f 1 + o f 1)) 2 7 Л 7 2 ⁷ к ⁷                   к ⁸

₊ ^^М З ^ш^ - ш^ 2 ⁸ п 8 1 ⁸ к ⁸

+ о©]

—

Поделив на z^Ml г " ¹ = 0, приравняем в (63) коэффициенты при одинаковых степенях к. При к⁰ имеем: 1 — 1 = 0 — верно, что символизирует о правильности выбора асимптотической формулы (60). Приравняв в (63) коэффициенты при к ⁷ , находим

М ^{7 (} Ш 1 ^— Ш 2 ^{) 8} ^ 7 (57) М ^{7 (} Ш 1 ^— Ш 2 ) ⁸                    (15),(16)

^,1 =--28П8--- =--2^--^^ + ^^=

(15Ы16) М7 sin8(п) Г 1 г-1             1 Гл

=      8,8   \j.L "^ + 67 Л,     V к Е N, М = ах1 + Ь(л — ж1).

Приравняв в (63) коэффициенты при к ^{- 8} , выводим

,    = М8 л — Ш2)8 + М8 sin8(л)Ag(^i)    ~-M7 „(Ш1-Ш2)5Ж, ।

^{8 к,} 1      ( — 2л?)2 ⁸ л ⁸ ? ⁸           ( — 2л?)16л ^{8        8}                      1у ^,1^,осн

//87-П1 Z^- -■ ^2-^    ], к Е N.(65)

Из формулы (57) имеем

7 8 =

.                   /            Г 1              1 + 72 "1       /

1 — (1 + V2)i = V⁴ + 2V2  ,        —           ? = V⁴ + 2У2е ^{-гф 1} ,

L 7 4 + 2 V2  74 + 2V2

1         1 + 72

—

ϕ 1

(    1 А ■ ( 1 + V2 ^

= arccos —.          = arcsin —          .

W 4 + 2^2/       V74 + 2V2/

Подставляя формулу (66) в (65) и сделав необходимые преобразования, находим

^ 8k,1 =

( — 1) ^{k +1} x/ 4 + 2^М ⁸ sin ⁸ ( ^п )Aq(x 1 ) 16 л ⁹

х sin

лах 1 к   л6(л — х 1 )к   лп 1    лМ ₇

М ⁺ ”8      8""

к Е N,

значение угла ф 1 приведено в (66), М = ах 1 + 6( л — х 1 ), М 7 = 7 7=1 ш ^ , значение А д (х 1 ) определено в (47).

Формулы (64), (67) показывают, что все коэффициенты асимптотической формулы (60) находятся единственным образом, мы привели явные формулы для их вычисления, поэтому теорема 5 полностью доказана.

• 7.    Вычисление первого регуляризованного следа дифференциального оператора (1)–(5)

Рассматривая аналогичным образом сектора 2), 3). . . 8) индикаторной диаграммы (рис. 1), докажем следующую теорему.

Теорема 6. Асимптотика собственных значений дифференциального оператора (1)– (5) в секторах 2), 3). . . 8) подчиняется следующему закону:

_ 2пг                         _ 2пг              _ 4пг S k,2 = s _k,1 6 ⁸ ; s _k,3 = 8 _к,2 в ⁸ = 8 _к,1 в ⁸ ;...;

_ 2пг            _ 2пг(т - 1)

S k,m = S _k,_m-1 6 ⁸ = 8 _к,1 в ⁸ m = 1,2,..., 8; к G N.

• 2)    При этом

^ k, 1 = ^s k,1 ; ^ k,2 = ^s k,2 = ^ k, 1 ; . . . ; ^k,m = ^s k,m = ^ k, 1 ,               ⁽⁶⁹⁾

m = 1,2,..., 8;    к G N.

Из формул (60), (68), (69) имеем sk,1 = Ak,1 = sk,m = Ak,m

^П [? i          i ^8d 8 k, 1          ¹ ^

M8 sin8(П) ' ^‘i1 + T + СЫ поэтому ряды

∞

∑︁

k =1

8         п8 к8         8n8^7k,i        8n8^sk,i k,1 + M8 sin8(п) + M8 sin8(п) + M8 sin8(п)к

∞