Формулы для расчета глубины проникания ударников различной формы в анизотропные преграды
Автор: Дубинский А.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (50), 2020 года.
Бесплатный доступ
Рассматривается высокоскоростное проникание ударников с подобными поперечными сечениями (пирамиды, не обязательно правильные, тела вращения, тонкие тела с произвольной формой поперечного контура) в преграды с динамической твердостью, непрерывно меняющейся в зависимости от глубины преграды. Описание взаимодействия барьера с ударником основано на модели Витмана-Степанова; эффекты, связанные с неполным погружением ударника в барьер на начальном этапе, не учитываются. Получены явные формулы, описывающие зависимость глубины проникания от скорости удара, формы ударника, механических свойств материала преграды.
Ударник, преграда, барьер, мишень, проникание, пробивание, анизотропия, глубина
Короткий адрес: https://sciup.org/147246573
IDR: 147246573 | УДК: 539.42+621.315.222+531.552+531.66 | DOI: 10.17072/1993-0550-2020-3-34-40
Текст научной статьи Формулы для расчета глубины проникания ударников различной формы в анизотропные преграды
Область применения функциональноградиентных материалов неуклонно расширяется, что стимулирует исследования в соответствующих областях [1-5]. Применительно к механике проникания это, прежде всего, экспериментальные исследования многослойных барьеров, состоящих из пластин с различными механическими свойствами, о чем свидетельствуют обзоры [6-7] и обзорные разделы монографий [8-9]. Теоретический анализ основан главным образом на модели, представляющей нормальное напряжение в точках поверхности проникающего тела, контактирующих с барьером, как квадратичную функцию нормальной компоненты локальной скорости с нулевым линейным членом ("модель Витмана–Степанова" [10]) либо на "законе плоских сечений" [11]. Обычно также принимаются дополнительные упрощения, в частности, предполагается, что нос ударника имеет форму прямого кругового конуса, иг- мишень; проникание; пробивание; анизотро- норируются особенности начального и конечного этапов проникновения, когда ударник не полностью погружен в преграду, и др. Несмотря на интенсивные исследования [8-9, 12-21], явные формулы для интегральных характеристик проникания (глубины проникания и баллистического предела) получить не удается, за исключением случая, когда фактически предполагается последовательное пробивание слоев [8, 9, 12].
В рамках подхода, характерного для механики проникания, обобщенного на случай анизотропной преграды, выполнена работа [22], в которой задача определения глубины проникания сведена к решению трансцендентного уравнения.
В настоящей работе рассматривается высокоскоростное проникание ударников с подобными поперечными сечениями (пирамиды, не обязательно правильные, тела вращения, тонкие тела с произвольной формой поперечного контура) в преграды с динамической твердостью, непрерывно меняющейся в зависимости от глубины преграды.
Получены явные формулы, описывающие зависимость глубины проникания от скорости удара, формы ударника, механических свойств материала преграды.
1. Постановка задачи и математическая модель
Рассмотрим высокоскоростное нормальное проникновение твердого, заостренного тела в полубесконечную преграду, твердость материала которой меняется в зависимости от глубины.
Предполагается, что взаимодействие снаряда с преградой описывается следующей двухчленной моделью, известной как модель Витмана-Степанова [10]:
dF = Y vn ' + Y ] n0 dS (1)
где γ – плотность материала преграды; Y – динамическая твердость материала преграды; dF - сила, действующая на боковую поверхность элемента снаряда dS , находящегося в контакте с пластиной (преградой), n 0 и vn , соответственно, единичный вектор внутренней нормали и нормальная составляющая мгновенной скорости снаряда в данной точке на поверхности снаряда.
Результирующая сила, действующая на снаряд в каждый момент времени, определяется интегрированием dF по боковой поверхности контакта снаряд–преграда в тот же момент времени Slat . В результате получается следующая формула для силы сопротивления D :
D = (-V0) •[[ dF = jj (-V0) • dF, (2) Slat Slat где v0 - единичный вектор скорости ударника.
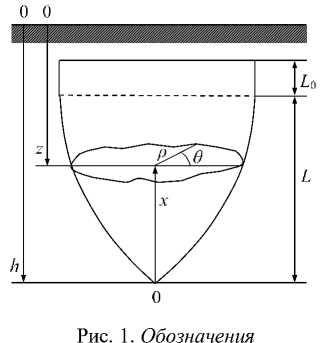
Далее мы используем следующие обозначения (рис. 1). Координата h , текущая глубина проникания, определяется как расстояние между носом ударника и поверхностью преграды.
Цилиндрические координаты x, р , 0 с началом координат в носовой части ударника связаны с ним, причем координата x направлена вдоль его оси. Уравнение р = Ф ( x, 0) , где Φ - выпуклая функция, определяет форму ударника, L – длина носовой части ударника, которая взаимодействует с преградой; он имеет также кормовую цилиндрическую часть длины L о .
Заметим, что поперечное сечение x = x о , расположено на глубине h о - x о , если нос ударника расположен на глубине h = h о .
В рамках предпринятой постановки задачи, в отличие от [22], учитывается различие показателя твердости в различных точках поверхности ударника.
Предполагается, что ударник имеет две плоскости симметрии, что обеспечивает его поступательное движение в преграде.
Нашей целью является получение явных формул для глубины проникания в преграду из материала, жесткость которого меняется в направлении проникания.
-
2. Ударники с подобными поперечными сечениями.
Математическая модель и формулы для глубины проникания
Ниже мы рассматриваем так называемые гомотетичные по форме ударники, имеющие подобные сечения, перпендикулярные его оси, вследствие чего функцию Ф ( x,0) можно представить в виде:
Ф ( x, 0 ) = р ( 0 ) • ^ (x ) . (3)
Для определенности предполагаем, что функция ^ ( x ) задает уравнение контура ударника в сечении 0 = о и о < x < L , а безразмерная функция р ( 0 ) - уравнение кормового сечения, перпендикулярного оси x , причем р (о) = р (2 п ) = 1 .
Пренебрегая эффектом, связанным с частичным погружением ударника в преграду на начальной стадии проникания, после несложных преобразований можно получить следующее выражение для D в случае модели, заданной уравнением (1) [8–9]:
где
D ( h , v ) = f , ( h ) v 2 + f/h ), (4)
x=L в=2n f,(h) = J dx Jd0[Y(h - x)ФФx] = x=0 в=0
где
L ix2)=J rn3 dx,
L 2n
= J ^ Y ( h - x ) dx J p 2( 0 )d 0 ,
0 =2 n
I ( 2)( x ) = J
0 =0
p6 d0
p 2( p2 ri + 1) + pe 2
x=L 0=2n f 2 = Y J dx J x=0 0=0
Ф 3 Ф 3 d 0
Ф 2( Ф x + 1) + Ф 0
x = L
0 =2 n
= Y J Wxdx J x=0 0=0
p6 d 0
p 2( p2 £ + 1) + p 0
причем f2 не зависит ни от x ни от 0 .
Тогда уравнение движения ударника массы m выглядит следующим образом:
m dv 2 у 2 к
+ f ’ v + f )( h ) = 0 , (7)
2 dh
и решение этого линейного относительного v 2 обыкновенного дифференциального уравнения при условии, что v (0) = vi mp ( vm p -скорость удара), может быть записано в виде:
v 2( h ) =
Qh
h vimp--f f0(h) Q(h)dh
m
, (8)
где
h
Q ( h ) = exp — \ f 2 d z = exp | f m-, mm
\ 0 7 v
\
. (9)
Используя условие v ( H ) = 0, получаем урав-
нение для определения глубины проникания:
H
J f 0 ( h ) Q ( h ) dh = mv mp . (10)
0 2
В разделах 3-4 мы рассмотрим классы форм ударников, для которых I(2 не зависит от x . В этом случае уравнение (10) приобретает вид:
H aIxx01<0) Jexp((в + кз)hdh = mvmp ,(16)
где кз = — I'x2' IУ ■(17)
m
Вычислив интеграл в левой части уравнения (16), получаем:
exp ( ( в + k 3 ) H )- 1 = k i vmp ,
, _ ym( в + к ) (18)
1 = 2 a I <0) I (0) ’ x 0
откуда
H = ^1^(1 + к 1 vmp ) . (19)
/^ + кз
Если понимать под баллистическим пределом так называемый "армейский баллистический предел" (скорость удара, при котором ударник достигает тыльной границы преграды), то заменяя H толщиной преграды b , а также v баллистическим пределом v , получим из формулы (19) явную формулу для v :
v bl = T [ exp ( b ( в + k 3 ) )- 1 ] . (20)
k 1
Для функции, описывающей динамическую твердость в зависимости от глубины преграды, выберем аппроксимацию [4–5]:
Y (z) = aexp( ^z),(11)
которая хорошо описывает возможные виды поведения зависимости Y(z) . Тогда f0 = aI^ I(0)exp( eh),(12)
где
L2
I^ = J Ж exp( - fix) dx, I(0) = J p 2(0) d0 (13) 0
и f2( h) = y ix2) I (2)( x),(14)
В частном случае изотропной преграды в = 0 , a = Y (0) = Y .
-
3. Ударники с конической формой носовой части
-
3.1. Общее решение
-
Пусть ударник имеет коническую форму носовой части, то есть, ее поверхность образована движением отрезка, проходящего через начало координат и скользящего по контуру, являющемуся границей между носовой и цилиндрической частями ударника.
Очевидно, класс таких "носов" не ограничивается прямыми круговыми конусами; к этому классу принадлежат также, например, пирамидальные тела.
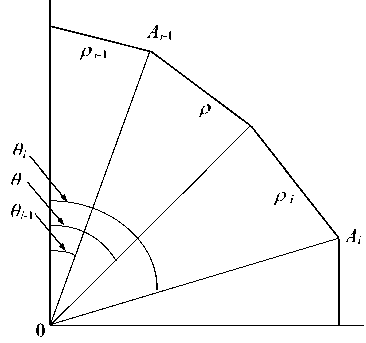
Рис. 2. Форма части поперечного контура ударника
Рассмотрим часть поперечного контура пирамидального тела (рис. 2), расположенную в области 0 ≤ θ ≤ π /2 , имея в виду, что контур симметричен относительно осей θ = 0 и θ = π /2 . Контур определяется точками с координатами ( θ 0 = 0, ρ 0 = 1),…, ( θ i - 1, ρ i - 1), ( θ i , ρ i ), ... , ( θ n = π /2, ρ n ), причем потребуем выполнения условий θ 0 < θ 1 < ... < θ i < ... < θ i < ... < θ n .
Уравнение прямой, проходящей через точки Ai - 1 и Ai , имеет вид:
ρ ( θ ) = ρ i
cos( θ + ω ) cos( θ + ω )
где уравнение для ω i получается после подстановки в (21) θ = θ i - 1 , ρ = ρ i - 1 :
ρi-1 cos(θi-1 +ωi) = ρi cos(θi +ωi) .(22)
Выражения (13) и (15) для I θ (0) и I θ (2) с учетом формул (21)-(22) и соотношений тригонометрии принимают вид:
Iθ(0) = 4∑n ρi cos(θi +ωi)Ψi = n i=1
= 4 ∑ ρ i -1 ρ i sin( θ i - θ i -1 ) = 2 S .
i =1
I(2)=4 n ρi4cos4(θi+ωi)
θ ∑i=11+ρi2cos2(θi+ωi)tg2ϑ i n ρi-1ρi3cos2(θi+ωi)sin(θi-θi-1)
i=1 1+ρi2cos2(θi+ωi)tg2ϑ где S - площадь сечения, ограниченного поперечным контуром, ϑ - угол при вершине треугольника в продольном сечении контура ударника при θ = 0 ,
Ψ= i dθ
θ ∫ cos2( θ + ω i )
=tg(θi +ωi)-tg(θi-1 +ωi)= sin(θi -θi-1)
cos( θ + ω )cos( θ + ω ).
Вычислив интегралы в выражениях (13)
(0)(2)
и (15) для I x и I x , получим:
L
I (0) = tg 2 ϑ ∫ x exp( - β x ) dx = 0
1 - ( L β + 1) exp( - β L ) β 2
tg 2 ϑ ,
L
I (2) = tg 4 ϑ ∫ xdx = 0.5 tg 4 ϑ L 2 .
В частном случае ромбовидного поперечного сечения n = 1 , θ1 =π/ 2 и, как обыч- но, θ0 = 0 , ρ0 = 1 . Тогда уравнение (22) при- водит к выражению для ω1 :
tgω1 = -1/ρ1 , sin2 ω = 1 / (1+ρ12)
и формулы (23)-(24) приобретают вид:
(0) (2)
θ = ρ1 , θ =
1 + ρ 12 / cos2 ϑ
-
3.2. Случай поперечного контура ударника, вписанного в окружность
Рассмотрим ударники, носовая часть которых может быть вписана в прямой круговой конус. Тогда
ρ = 1, i = 1,2,.., n . (30)
Уравнение (22) приводит к соотношению cos( θ i - 1 + ω i ) = cos( θ i + ω i ) , откуда следует, что θ i - 1 + ω i = - ( θ i + ω i ) и, следовательно,
ω i = - 0,5( θ i - 1 + θ i ) . (31)
В рассматриваемом случае соотношения (23) и (24) примут вид:
W = 4 £ sinc e , - e , -, ) , (32)
i =1
n cos2 1 ei - i - 1 ' I sinc e - e J
I ^= 4 z— 1 2 Лв a —. (33)
1 = 1 1 + cos2 1^ - 1 I tg 2 &
I 2 J
-
3.3. Случай носовой части ударника в форме правильной пирамиды
В этом случае к условиям (30) добавляется равенство т (0)
I не вызывает принципиальных затруднений; например, для тела вращения р = 1 и, следовательно, I ^2) = 2 п .
Что касается описания продольного контура, то не представляет большого труда найти аппроксимации, позволяющие совместить требования выпуклости и тонкости тела с простотой вычисления интегралов I *0) и I *2). Пусть, например, форма продольного контура ударника задается в виде:
_ . । п x I „
^ ( x ) = R sin I--1 , 0 < x < L .
I 2 L J
e = 0.5x1/n, i = 1,2,..,n , соотношения (32) и (33) преобразуются ду:
к ви-
Тогда ^ (0) = 0 , ^ ( L ) = R и
I (0) = 4 n sin( 0.5 п/ n ) , I (2) _4И cos 0 (O.05 П n )sin(0.5 n/n ) e ~ 1 + cos2(0.25 ^ n ) tg P
, . п R ( п x I
^ ( x ) =--cos I--I , x 2 L I 2 L J
.
^ xx ( x ) =
п2 R
4 L2
. I п x I sin II , I 2 L J
-
3.4. Случай носовой части ударника в виде прямого кругового конуса
Соответствующие формулы можно получить, переходя в соотношениях (35)-(36) к пределу при n ^ да ; в результате получаем:
I '0) = 2 п , I f) = 2 п cos 2 $ . (37)
-
т. е. ^ ( x ) - возрастающая, выпуклая вверх
4. Тонкие ударники
функция на интервале (0, L).
Интегралы I’0) и Ix22 легко вычисля ются:
(0) _ 0. 25 п R г / о т , 1-1 у(2) _ п R /42) Ix = n^l Lexp( P L + 1] , Ix \гт2 .(42)
в L + п 16 L
Эти формулы можно получить из соотношений (13) и (15) для I(0) и I(2 , подставив р ( е ) = 1 и ^ ( x ) = tg $ x .
Для тонких ударников (не обязательно конических) справедливо условие:
Р2^ x << 1 , (38)
с учетом которого формула (15) для I ^2) приобретает вид
В качестве одного из универсальных методов расчета интегралов I x0 и I x22 может быть использован подход, основанный на кусочно-линейной аппроксимации продольного контура.
В этом случае получаем формулы:
N i^ «z
1 = 1
p (x)exp( -e x/> +p (x^ Дхх
^ ( x ) - ^ ( x - 1 ) х
A x
0 2п
IP = f e=о
р 6 de
, р + р 0
I У «У
x
^ < x J± ^ ( x = 1 ) ^х
Ф ( x 1 ) - Ф ( x - 1 ) A x
, (44)
а формулы (13), (15) для Ix0 , Ix2 , I ^0) и формулы (19), (20) для H и v остаются без изменений. Вычисление интегралов I *2) и
где N + 1 - количество точек аппроксимации (включая x 0 = 0 ), xN = L , A x = L/N , x = 1 A x , 1 = 1,2,..., N .
Очевидно, увеличивая N , можно добиться нужной точности аппроксимации.
5. Ударники формы тела вращения
В случае ударника, имеющего форму тела вращения (не обязательно тонкого), формулы (18)–(19) остаются в силе, но
I θ (0) = 2 π , k = 4 πγ L ϕϕ x 3 dx . (45)
m 0 ϕ x 2 + 1
Список литературы Формулы для расчета глубины проникания ударников различной формы в анизотропные преграды
- S. Suresh and A. Mortensen. Fundamentals of functionally graded materials: processing and thermomechanical behaviour of graded metals and metal-ceramic composites. IOM Communications, London. 1998.
- Birman, V., and Byrd, L. W. Modeling and analysis of functionally graded materials and structures // Applied Mechanics Reviews. 2007. Vol. 60. P. 195-216.
- Larson, R. A., Palazotto, A. N., Gardenier, H. E. Impact response of titanium and titanium boride monolithic and functionally graded composite plates. // AIAA Journal. 2009. Vol. 47(3). P. 676-691. DOI: 10.2514/1.38577
- Khan T., Zhang N., Akram A. State of the art review of Functionally Graded Materials. In: 2nd International Conference on Computing, Mathematics and Engineering Technologies. 2019. P. 1-9.
- Guo L.C., Wu L.Z., Zeng T., Cao D.H. The transient response of a coating-substrate structure with a crack in the functionally graded interfacial layer // Composite structures. 2005. Vol. 70(1). P. 109-119.


