Fredgolm integral tenglamalarini rezolventa yordamida yechish

Ushbu integral tenglamani rezolventa orqali yechilishini qaraylik:

x ) ^{— 1} j y ^ ⁽ y ) dy =

3 _x e^x

—

1 x 1

e e —   ,

Bu yerda K ( x , y ) = y , Л = ^

Iteratsiyalangan yadrolarni hisolaymiz:

K2 (x, y) = j K (x, t) K (t, y) dt = | tydt = y, 0                       0

ii

K,( x, y) = J K (x, t) K2( t, y) dt = y j tdt = £, 0                       2 0

K,( x, y) = IK (x, t) KH ( t, y) dt = -y2 J tdt= £

0                      2   0

formulaga asosan berilgan tenglamaning rezolventasini hisoblaymiz

.I .1 i-V 1 У

R x ’ ^У ’~     ^ i — - 1 i — 1 - 1

V      ² / i = 1 ^{2   2}

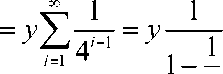
⁴ У

.

(15) formulaga asosan tenglamaning yechimini quyidagi ko’rinishda topamiz:

^ ( x ) = e x

xe

—

1 f 4 y ( 3

e

1 + ⁱ i ⁴ y

2  2 ¹ 3 V 2

y

-

1 У

2 ^ye

-

- dy =

= 1(3 — x ) e x + 1(3 — e ).

Misol. Ushbu     ^ ( x ) — A J ^ ( y ) dy = 1                     (1)

tenglama berilgan bo’lsin. Bu yerda a = 0, b = 1, K ( x , y ) = 1, M = 1 bo’lib, ketma-ketlik | A <  1 bo’lganda yaqinlashuvchi bo’ladi. Lekin bu tenglamani ketma-ket yaqinlashish usulidan foydalanmay ham osongina yechish mumkin. Shu 1

maqsadda                  J ^( y) dy integral biror noma’lum o’zgarmasdan iborat ekanligini e’tiborga olib, uni C orqali belgilab olamiz. U holda (1) tenglamaga asosan ^( x) = 1 + AC

Bu ifodani (18) tenglamaga qo’yib,  (1 - Л ) C = 1

bo’lgan barcha λ lar uchun yechimga ega. Haqiqatdan ham, (2) dan C =      ,

1 - Л demak, ^(x) = —-—. Buni (18) tenglamaga qo’yib, uni qanoatlantirishiga 1 - Л ishonch hosil qilish qiyin emas.

Endi (18) tenglamadan farqli, ozod hadi (0,1) oraliqda ixtiyoriy uzluksiz f (x) funksiya bo’lgan  ^( x) - Лf^( y) dy = f (x)            (3)

^C = f ^ ⁽ У ) dy

tenglamani tekshiramiz. Avvalgiday deb belgilab,

^( x) = f (x) + ЛС tenglikni hosil qilamiz. Buni 0 dan 1 gacha integrallab, C ni topish uchun

(1 - Л ) C = f f ( x ) dx

tenglamaga ega bo’lamiz. Agar Л ^ 1 bo’lsa,

C = Уут f f ( x ) dx ,

^{1 Л} 0

^ ^{( x} ) = ^{f ( x} )

λ

1 - Л

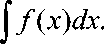
Bu funksiyani (3) tenglamaga qo’yib, uni qanoatlantirishiga ishonch hosil qilamiz, demak, (3) tenglama Л ^ 1 bo’lganda yechiladi va yagona yechimga ega bo’ladi.

Endi Л = 1 bo’lsin. Bu holda (4) tenglama j f (x) dx = 0

ko’rinishga ega bo’ladi. Agar f ( x ) shunday funksiya bo’lsaki, (5) tenglik o’rinli bo’lmasa, (3) tenglama yechimga ega bo’lmaydi, xuddi shunday bo’lishini f ( x ) = 1 da ham ko’rgan edik. Agar (5) tenglik bajarilsa, u holda C aniqlanmay qoladi , bu holda (3) tenglama ^ ( x ) = f ( x) + C

(C-ixtiyoriy o’zgarmas) ko’rinishdagi cheksiz ko’p yechimlarga ega bo’ladi. Misol. Rezolventani yadrodan foydalanib toping.

K ( x , t ) = x - 2t ,  0 <  x <  1,0 <  t <  1

Yechish. Quyidagicha belgilab olamiz, C _o = 1, B _o ( x , t ) = x - 2t

Yuqoridagi formulalardan foydalangan holda misolni yechamiz.

C = j (-s ) ds =

x - 2t  1                                   2

B j —--- f ( x — 2 s )( s — 2 1 ) ds — — x — t + 2 xt +—

1 о      J                                               3

C = (—2 s + 2 s2 + -) ds =

2 J                3       3

B 2 =

x-2t   1                  2

--2 j ( x — 2 s )( — s — t + 2 st + -) ds = 0

3        ^J0                            3

C ₃ = C ₄ = ... = 0,    B ₃ ( x , t ) = B ₄ ( x , t ) = ... = 0.

Л  Л2                                      2.

D ( Л ) = 1 +---1-- ; D ( x , t ; Л ) = x — 2t + ( x + 1 — 2 xt —) Л

2   6                                  3

24„ x — 21 + (x +1 — 2 xt —)Л

R(x, t;Л) =--------——^---3—

1 + —+ —

2   6

Nazariy va amaliy jihatdan muhim va ahamiyatga ega bo’lgan fizika, mexanika, texnika va boshqa sohalar masalalari integral tenglamalar usuli bilan

yechiladi. Ayniqsa, matematik fizikada tekshiriladigan masalalarni yechishda integral tenglamalarning ahamiyati kattadir. Shunday integral tenglamalarni rezolventadan foydalanib yeshish esa birmuncha qiyinchiliklarga barham beradi. Masala qanchalik murakkab bo’lishidan qat’iy nazar agar undan hayotda foydalanolmas ekanmiz yoki uning olam va insoniyat uchun foydasi tegmas ekan u qadrsiz bo’lib qolaveradi. Xuddi shunday integral tenglamalarni talabalar o’rganayotgan paytta hayotga tadbiqini bilmas, mohiyatini tushunmas ekan u talabalar uchun oddiy qog’oz parchalari bo’lib qolaveradi. Integral tenglamalarni tushuntirayotgan paytimizda talabalarga quyidagi hayotiy misollar bilan tushuntirib o’tsak maqsadga muvofiq bo’lar edi deb o’ylayman. Ya’ni ipning tebranishi, moddiy nuqtaning og’irlik kuchi ta’siridagi harakati kabi integral tenglamaga keladigan masalardan foydalanish mumkin.

Bu maqolada Fredgolm tenglamalarni rezolventadan foydalanib yechish uchun nazariy ma’lumotlar va namunaviy misollar keltirib o’tildi.

Foydalanilgan adabiyotlar

• 1.    С.Г.Михлин «Лекции по линейним интегральним уравнениям» Москва 1959

• 2.    М.Л.Краснов    «Интегральные уравнения введение в теорию»

• 3.    М.Л.Краснов, А.И.Киселев, Г.И.Макаренко    «Интегральные

  уравнения» Москва 2003

• 4.    Салахитдинов М. Мирсабуров.М «Нелокальные задачи для уравнений смешанного типа сингулярными коэффициентами» Ташкент 2005

• 5.    Соболев.С.Л «Уравнение математической физики» Москва 1954

• 6.     http://vilenin.narod.ru/Mm/Books/

• 7.     http://www.allmath.ru/

  "Экономика и социум" №5(96) 2022

Москва 1975