Функционал энергии для нелинейной задачи магнитостатики

Эффективным методом исследования и решения эллиптических краевых задач является энергетический метод. Квадратичные функционалы для линейных эллиптических краевых задач построены в монографиях [2, 5] . Применительно к нелинейным краевым задачам энергетический метод изложен в монографии [6] .

В настоящей работе энергетический метод реализован для задачи, возникающей при сведении задачи магнитостатики к одному квазилинейному уравнению для потенциала.

Исходная краевая задача для системы уравнений первого порядка с неизвестными векторными функциями предварительно преобразована в задачу для скалярного потенциала.

Использованы материальные уравнения, обладающие свойствами, характерными для магнитной проницаемости ферромагнетиков, однако с существенным ограничением. Рассматриваются только однозначные функции, то есть исключен гистерезис, для моделирования которого необходим совершенно иной математический аппарат.

Доказаны существование и единственность обобщенного решения задачи для потенциала в пространстве W2 1) (Q) . Такое решение позволяет построить решение исходной задачи, принадлежащее L 2 (Q) .

1 Формулировка краевой задачи

Трехмерные стационарные уравнения магнитостатики имеют вид [4] :

rot H = j div B = 0,                              (1)

где H — напряженность магнитного поля, H — его модуль, B — магнитная индукция, деленная на магнитную проницаемость вакуума ^ д , j — заданное пространственное распределение плотности тока.

Для разрешимости первого уравнения должно быть выполнено условие div j = 0, поскольку div rot = 0.

Предполагаем, что область Q — ограниченная и ее граница Г — гомеоморфная сфере дважды непрерывно дифференцируемая поверхность. Нормальную и касательные к границе компоненты векторов будем отмечать индексами n и l .

Если за границей рассматриваемой области находится идеальный проводник, то на границе обращается в нуль нормальная компонента магнитной индукции B . Условие может быть и неоднородным:

где q — заданная функция.

Для разрешимости задачи заданная функция q должна удовлетворять условию

У qd r = 0 .                         (3)

В противном случае получим противоречие, проинтегрировав второе уравнение (1) по всей области и (2) — по всей границе, поскольку интегралы левых частей равны в силу теоремы Гаусса — Остроградского. Предполагаем, что q является ограниченной функцией в пространстве L 2 (r)

У q ² d r <  c l <  от . (4)

2 Материальные уравнения — модель среды

В ферромагнитных средах связь между векторами B и H является нелинейной. Исключив из рассмотрения явление гистерезиса, полагаем такую связь однозначной. В дополнительном предположении изотропии среды принято записывать эту связь как

B = xh ) h .

Функция ^ ( H ) определяет зависимость относительной магнитной проницаемости от H и может быть разной в разных точках пространства, если ферромагнетик неоднороден, ^ = 1 вне магнетиков.

Построим функцию E ( H ) исходя из соотношения:

B =

dE ( H ) dH

Эта функция будет играть роль плотности магнитной энергии, деленной на µ 0 . Отметим, что выбор такой энергии связан с дальнейшим переходом к скалярному потенциалу. Если сводить исходную задачу к задаче для векторного потенциала, следует взять в качестве энергии интеграл от HdB.

В силу изотропии среды аналогичным (6) соотношением связаны и векторы B и H :

dE ( H )

d h .

Полагаем E (0) = 0 . Тогда из (5, 6) следуют выражения:

^ = H dEH , E ( H )= / H ^hdh.         (8)

Из (5) получаем связь между малыми изменениями векторов B и H :

dB i = ^ dH j ,                       (9)

’ = ' + dH н ,

δ ij — символ Кронекера.

Воспользуемся известными свойствами ферромагнетиков, чтобы показать равномерную положительную определенность этого тензора.

Если ориентировать ось z декартовых координат вдоль вектора H , то тензор а (10) становится диагональным

/ v  00

а=I 0 v°

\ 0 0 v + dH

Отличие B от H обусловлено намагниченностью вещества M :

B = H + M .

Мы рассматриваем изотропные среды, поэтому векторы B , H , M параллельны. В ферромагнетиках вектор M направлен в ту же сторону, что и H , и по величине не убывает с ростом H . Все три вектора равны нулю только при B = 0 . Поэтому суммируются модули

B = н + M,

B ( H ) является строго монотонной функцией:

dB

dH - 1, и магнитная проницаемость

V = B/H - 1 .

Направим вектор d H параллельно H , то есть возьмем dH x = dH y = 0 , dH z = dH . Тогда в силу (11)

dB =

V + H~^

dH,

и из (12) получаем

V + H^ - 1 .

dH

При дополнительном предположении об ограниченности B/H и dB/dH получаем

1 ^- V =   ^- №,

H dµ dB

¹ - ^{V +} HdH = dH - ^{V 1} ,                ⁽¹³⁾

и, значит, тензор a (11) является равномерно положительно определенным. Его собственные значения в любой точке области Q лежат в интервале (1 ,^ 1 ) :

A 2 - A T a A - V 1 A 2 , (14)

где A — произвольный вектор. Это условие является более сильным, чем условие эллиптичности для сформулированного в следующем параграфе квазилинейного уравнения для потенциала:

AT a A > 0, при выполнении которого вариационная задача регулярна [3]. Однако для ферромагнетиков условие справедливо именно в более сильной форме (14).

Отметим, что для реальных ферромагнетиков функция ц ( Н ) действительно ограничена, но если перейти к прецизионным измерениям, обнаруживается, что B ( H ) изменяется не гладко, а микроскопическими скачками, то есть функция dB/dH бывает бесконечной и последнее неравенство (13) несправедливо. Налагая это условие, мы ограничиваемся рассмотрением только макроскопических или сглаженных зависимостей.

В силу (8) из неравенств (13) получаем

H 2 / 2 - E ( H ) - V 1 H 2 / 2 .                   (15)

В пустоте неравенства (13 - 15), естественно, превращаются в равенства и V 1 = 1 , поскольку тогда ц = 1 , a = d ij , E = H 2 / 2 .

3 Задача для скалярного потенциала

Один из методов решения задачи (1, 2, 5) основан на предварительном построении вспомогательной функции H I , имеющей смысл напряженности магнитного поля при тех же заданных токах, но в пустоте:

rot HI = j div Hi = 0 (Hi )n|r = 0.

Решение этой линейной задачи сравнительно просто. Обычно она сводится к задаче для векторного потенциала. Можно использовать энергетический метод [1] .

Разность H - H I в силу первых уравнений из (1, 16) имеет нулевой ротор, и, значит, может быть введен скалярный потенциал ϕ, такой, что

H = H i — grad^.

Первому уравнению из (1) такое H удовлетворяет автоматически, поскольку H I есть решение (16), а оставшиеся уравнения (1, 2, 5) образуют краевую задачу для ϕ :

div ( ^ (| H i — grad ^ | )( H i — grad ^ )) = 0

∂ϕ

- M|H i - grad^ [) дП

= q г

j ^d Q = 0 .

Чтобы исключить несущественную аддитивную постоянную, зафиксировано среднее значение ϕ .

4 Функционал энергии

Рассмотрим множество гладких функций ϕ , удовлетворяющих только последнему условию (17).

Построим следующий функционал энергии:

W ( ^ ) = У E ( | H i - grad^ l) d Q + ^^qd F .

В силу неравенства Коши — Буняковского и (4) линейная часть функционала ограничена в L 2 (r) :

^2df, и также в TW21) (Q), поскольку последнее пространство вложено в L2(r):

|

^qd r| <  c 2 k ^ k .

В силу теоремы об эквивалентных нормах для функций с нулевым средним и неравенства Пуанкаре для таких функций [7] можно использовать следующую норму ^ в ^W^ ¹ ) (Q) :

1И2 = /

( grad^)² d Q .

Нелинейная часть функционала энергии в силу (15) оценивается снизу:

/ E ( | H i

— gradp I) d a > -

j ( H i — gradpfd tt >

>2 /(grad p)² d a - I У H i gradpd ai + - У H I ² d a .

Фигурирующий здесь линейный функционал оценим с помощью неравенства Коши — Буняковского:

У H i grad pd a

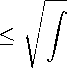
H I d a

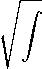
( gradp^d a .

Первый сомножитель ограничен, а второй есть норма ϕ в пространстве W ₂ ⁽¹ ) (a) .

Таким образом, значения функционала энергии оценены снизу:

W ( p ) > 2 \\ p f —

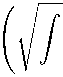
H I d a + c i

k^Pk + 2 / H d ^a .

Значения этой квадратичной формы от k ϕ k ограничены снизу, поскольку интеграл от векторной функции H I ограничен, так как H I является решением задачи (16).

Поэтому существует точная нижняя грань значений W(p) и можно построить минимизирующую последовательность ϕ k :

W ( p k ) ^ d, W ( p k ) >  d.

Без ограничения общности считаем k ϕ k k ≤ M , поскольку в силу (19) при неограниченном возрастании Ip || значение W ( p k ) ^ от .

Введем в рассмотрение еще одну последовательность гладких функций ψ _k , имеющих нулевое среднее и ограниченную норму:

k ψ k k ≤ M.

Рассмотрим значения функционала энергии на последовательности функций p k + Еф k , где е — произвольное число:

W ( p k + Еф k ) = У E (| Н |

— grad p k — е grad ф k |) d a+

+

У p k qd r

+ Е

j> ф k qdr.

По формуле Лейбница

E ( | H i - grad^ k - egrad^ k |) = E ( | H i - grad^ k |) + У |E d H = = E ( | H i - grad^ k |)+

+ У (- egrad^ k ) ^T B ( H i - grad^ k - tegrad^ k ) dt,

где t — параметр, изменяющийся от нуля до единицы. Производная дЕ/д H равна B ( H ) в силу выражения (6) и параллельности векторов B и H .

Аналогично при фиксированном t с учетом (7) и (9):

∂E ∂H i

∂E ∂H i

H I - grad ϕ k

3       _∂ 2 _E

⁺ ^J IH i lH j d j

t

= B ⁽ H i ^- grad^k) + X У ih C j =1 ₀      ^j

-e— — I dT =

t

3             ∂ψ

= B ( H i - grad^ k ) - e^ I    & ij dT I — .

j =1   ₀               ^j

Подставив это выражение в (22), получаем

E ( | H i - grad^ k - egrad^ k |) = E ( | H i - grad^ k |)-

1 t

2 У dt J dT& > grad^ k .

- e B ( H i - grad^ k ) grad^ k + 2 ( grad ^ k ) T

Выражение в фигурных скобках есть симметричный тензор & ^д , поскольку он получен суммированием симметричных тензоров. Поскольку векторы grad ψ k не зависят от t, τ они могут быть внесены под знаки интегралов, и в силу (14)

1 t

2 У dt ^ dT I ( grad^ k ) ² <  ( grad^ k ) ^T d ^ grad^ k <  00

( 1 t \

2 /dt/d ^T I ( grad^ k ) 2 .

Поскольку фигурирующий здесь удвоенный интеграл равен единице, получаем для & ^Л оценки, аналогичные (14):

A ² <  A T & ^д A <  _WA ² .

В отличие от & тензор & ^Л определяется парой значений H . В рассматриваемом случае это H I - grad ϕ k и H I - grad ϕ k - ε grad ψ k .

Подставим выражение (23) в (21)

W ( ^ k + E^ k ) =

^У E ( | H i — grad^ k l) d Q + j> ^ k qd C

+

+ e (— ! ^{b ( h} i — grad^ k ) grad^ k d Q + У ^ k qd^ ε ²

+ — / ( grad^ k ) T ^grad^ k d Q -

Напомним, что компоненты тензора & ^Л не являются заданными функциями координат. В силу (20) и (24) последнее слагаемое оценивается сверху величиной:

ε ²

-2 ^М 2 -                            (26)

Первое слагаемое в (25) есть значение функционала энергии на элементах минимизирующей последовательности. Поэтому можно взять достаточно большое число k 0 , такое, что при k > k 0 отличие этого слагаемого от d будет меньше величины (26).

Поскольку d есть точная нижняя грань, то

W ( ^ k + E^ k ) — d > 0 .

С учетом ограниченности первого и последнего слагаемых (25) при k > k 0 получаем

^д ^ М ² + e У У B ( H i — gradg k ) grad^ k d Q + У ^ k qdT^ + ^g ^ M ² > 0 .

Осталось выбрать знак ε , противоположный знаку выражения в квадратных скобках, чтобы получить оценку:

I - /B ( H I — gradg k ) grad^ k d Q + У ^ k qd Tl < | - | g 1 M ²

при k >  k o , | e | = 0 . Поскольку e - произвольное число, а левая часть от ε не зависит, полученное неравенство означает, что

— У B ( H i — gradg k ) grad^ k d Q + У ^ k qdT ^ 0 .

Для k > k o , m > k o возьмем ^ k = ^ k — ^ m . Это возможно, поскольку нормы ϕ k , ϕ _m ограничены. Тогда из (27) для ϕ k и ϕ _m получаем

/ ^B( H I — grad^ k ) grad &k

-

^ m ) d Q +

У ( ^ k — V m ) qdT

^ ⁰ ,

B ( H I — grad ^ m ) grad ( ^ k

-

- m ' d Q + У

⁽ ^ k - ^ m )^{q dr} ^ 0 .

Вычтем первое из второго:

( B ( H I — grad^ k ) — B ( H I — grad^ m )) grad ( ^ _k — ^ m ) d Q ^ 0 . (28)

При конечном изменении напряженности магнитного поля на величину ^ H изменение 5 B получим интегрированием (9), положив d H = dtδ H , где параметр t изменяется от нуля до единицы:

5 B = у d B = у & ( H ) d H = у & ( H ) 5 H dt = (y & ( H ) dt ) S H .

Обозначим полученный тензор как & ⁵ . Для декартовых компонент

SB i = ^j Щ.

Тензор & ⁵ симметричен, поскольку получен суммированием симметричных тензоров. Рассмотрим квадратичную форму:

5 H T а ⁵ ^ Н

Z 1

5 H T d( H ) 8 H dt.

В силу положительной определенности &  (11, 13) при любом H имеем:

( 5 H ) ² <  5 H T & ( H ) 5 H <  p i ( 5 H ) ² .

Поскольку правая и левая части не зависят от параметра t , интегрированием этих неравенств получаем:

( 5 H ) ² <  5 H T & ⁵ 5 H < _W( 5 H ) ² ,

и, значит, тензор & ⁵ обладает тем же свойством равномерной положительной определенности, что и а (14). Отметим, что эти оценки не зависят от H и от δ H , хотя сам тензор & ⁵ изменяется при изменении этих параметров.

В силу (29) из (28) следует:

У ( grad ( p k - P m )) d Q ^ 0 .

Поскольку пространство W^^ Q) полное, то существует, причем единственный, предельный элемент ϕ и

У ( grad ( p k — р )) ² d Q ^ 0 .

Для ϕ из (27) следует тождество:

— У B ( H i — gradp ) grad^d Q + (^ ^q d r = 0 ,       (31)

справедливое для любой функции ψ , принадлежащей тому же множеству функций, что и ϕ .

Если предельная функция ϕ является гладкой и решение задачи (17) H I тоже гладкое, то можно интегрированием по частям преобразовать тождество (31):

У ф div ( B ( H i — grad p )) d Q —

У ф ( В _п — q ) d r = 0 .

Поскольку функция q удовлетворяет условию (3), добавление константы к ψ не влияет на тождество. Поэтому здесь произвол ψ фактически не ограничен условием нулевого среднего значения ψ . Поэтому из (32) обычным образом [5] получаем:

div ( B ( H i — grad p )) = 0

B n | r = q.                               (33)

В силу граничного условия (16) это граничное условие эквивалентно граничному условию (17). Лишь формой записи отличаются и первые уравнения (33, 17).

Таким образом, функция ϕ , доставляющая минимальное значение функционалу энергии, в случае гладкости позволяет построить решение краевой задачи (17) и тем самым исходной задачи (1, 2, 5) по формулам:

H = H I — radp

B = № )H, где HI — решение вспомогательной линейной задачи (16).

Если функция ϕ не является гладкой, ее следует рассматривать как обобщенное решение в смысле справедливости тождества (32) для про- извольной функции ψ. Существование, единственность и принадлежность обобщенного решения пространству W^1)^) доказаны.

Несложно доказывается и обратное утверждение: решение краевой задачи (17) доставляет минимальное значение на множестве функций

ϕ с нулевым средним значением. Пусть ϕ — решение этой задачи. За-

пишем функционал энергии (18) для функции вида p + еф в форме

(25):

W ( р + еф) =

/ E ( | H i

— gradp |) d Q +

У pq dr^

+

+ е —- У B ( H i — gradp ) gradфd Q + У фqdГ^ +

Е ²

+ ~2    ( gradф ) ^T o^ ^ gradф d Q .

Поскольку ϕ — решение краевой задачи, тождество (32) удовлетворено при любой функции ψ . Интегрированием по частям из него получаем (31), и, значит, коэффициент при ε в (34) равен нулю. Коэффициент при е ² положителен, поскольку тензор & ^ удовлетворяет равномерным оценкам (24) и интеграл от квадрата градиента ψ строго положителен для любой ненулевой функции ψ с нулевым средним значением. Первый член в (34) есть W(p).

Поэтому

W ( p + еф ) >  W ( p )

и равенство достигается только при е = 0 , то есть минимум W достигается на функции ϕ .

Заключение

Таким образом, основная краевая задача магнитостатики с помощью построения решения вспомогательной линейной задачи сведена к задаче для одного квазилинейного эллиптического уравнения для скалярного потенциала.

В рамках энергетического метода доказаны существование и единственность обобщенного решения полученной задачи для потенциала, которые позволяют построить магнитное поле, являющееся решением исходной задачи.

Предложенный и обоснованный принцип минимума фукционала энергии целесообразно использовать при численном решении задач магнитостатики.