Гармонические функции и теория потенциала
Автор: Кибирев В.В.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Математика
Статья в выпуске: 6, 2007 года.
Бесплатный доступ
В статье рассматривается связь гармонических функций с потенциалом распределения масс в некоторой области трехмерного пространства. Доказаны две теоремы о том, что если плотность масс ограничена и интегрируема в области, то потенциал и его первые производные равномерно непрерывны, а также если плотность потенциала удовлетворяет условию Гельдера, то этот потенциал удовлетворяет уравнению Пуассона.
Короткий адрес: https://sciup.org/148183765
IDR: 148183765
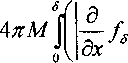
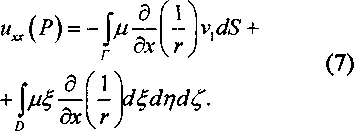
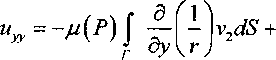
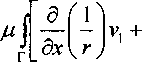
Список литературы Гармонические функции и теория потенциала
- Бицадзе А.В. Краевые задачи для эллиптических уравнений второго порядка. -М.: Наука, 1966 -204с
- Гобсон Е.В. Теорема сферических и эллипсоидальных функций. -М.: ИЛ, 1952. -476с.
- Курант Р. Уравнения с частными производными. -М.: Мир, 1964. -830 с.
- Якушаускас А. К задаче о наклонной производной для эллиптических уравнений//Сиб. мат. журн. -1975. -1. 16. -№ 2. -С. 405-40».
- Якушаускас А. Аналитическая теория эллиптических уравнений. -Новосибирск: Наука, 1979.-192с.
Статья научная
