Газодинамика вакуумно-импульсной сушки пищевых продуктов

Введение. Сушка – один из старейших методов консервирования, используемый в пищевой промышленности. Эта технология развивалась, и применялись различные системы сушки, такие как конвекция, кондукция или излучение, а также их комбинации. Различные аспекты современных технологий сушки приведены в работах [1–7]. Вакуумная сушка широко используется в пищевой технологии для интенсификации процесса, является предпочтительной технологией сушки из-за более высокого качества конечных продуктов [1, 4].

В обзоре [2] изучается процесс, который основан на электромагнитном излучении, испускаемом магнетроном на пищевой матрице в среде вакуума и преобразующемся в тепло. Это перспективный, быстрый и эффективный процесс снижения содержания влаги. Исследования этого процесса и его промышленное использование выросли примерно на 300 % за последние 20 лет.

Вакуумная жарка известна как самый популярный способ обработки пищевых продуктов для производства готовых к употреблению закусок. Количество масла, используемого для жарки, при вакуумном способе жарки меньше по сравнению с другими способами жарки [3].

Управление параметрами микроволновой вакуумной сушки способствует получению высококачественных конечных продуктов [5–7].

С помощью магнитно-резонансной томографии в работе [8] было предложено сопряженное моделирование импульса, тепломассопереноса и структурной деформации при вакуумном охлаждении хлеба на пару.

Оценка влияния выбранных методов предварительной обработки, таких как вакуумноосмотическая дегидратация, вакуумно-ультразвуковая обработка и вакуумно-осмосоническая обработка, на метаболомы и качественные характеристики высушенных в инфракрасном диапазоне ломтиков имбиря произведена в [9]. Установлено, что предварительная вакуумно-осмосо-ническая обработка имбиря перед сушкой имеет большой потенциал для крупномасштабного промышленного применения.

Микроволновая вакуумная сушка концентрированного обезжиренного молока и свойства получаемого в результате порошка изучены в очень ограниченной степени [10]. Результаты исследования микроволновой вакуумной сушки концентрированного обезжиренного молока и рекомендации по производству сухого молока или сохранению заквасок в молочной матрице приведены в работе [10].

В [11] рассмотрены вопросы вакуумной сушки рыбной кости трески и судака. Предложен экспериментальный стенд. С применением методов планирования эксперимента установлен характер влияния температуры и давления на скорость сушки.

Вакуумно-импульсные сушильные камеры (рис. 1) применяются в промышленных масштабах [12, 13].

Цель исследования – сформировать математическую модель газодинамических процессов, происходящих при вакуумно-импульсной сушке, и проанализировать их зависимость от определяющих параметров.

Объекты и методы. В установке вакуумноимпульсной сушки происходят два основных газодинамических процесса: откачивание воздуха из ресивера с помощью вакуумного насоса (сравнительное медленное) и выравнивание давления вакуумной камеры с ресивером (импульсное).

Для моделирования первого этапа необходимо знать нагрузочную характеристику вакуумного насоса - зависимость производительности от давления в ресивере. В вакуумно-импульсных установках используются низковакуумные насосы (водокольцевые, пластинчато-роторные и др.).

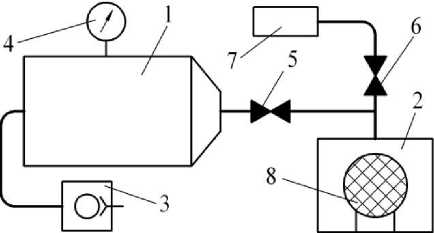
Рис. 1. Установка вакуумно-импульсной сушки: 1 – ресивер; 2 – вакуумная камера; 3 – вакуумный насос; 4 – вакуумметр; 5, 6 – кран шаровой; 7 – нагреватель; 8 – емкость с продуктом [13]

Здесь рассмотрим работу водокольцевого насоса. Воспользуемся ранее разработанным методом моделирования нагрузочных характеристик вакуумного насоса [14–16]. Для примера возьмем насос российского производства ВВН1-1,5. На рисунке 2 точками показаны экспериментальные данные [17]. Они могут быть аппроксимированы зависимостями

N(P) = A o + A i • P, при P o <  P <  P a ,                       (1)

Q(P) =

B ₀ + B 1 • P + B 2 • P ² + B 3 • P ³ + B 4 • P ⁴ , при P_o <  P <  P * ;

Q * = const, при P * <  P <  P a .

Эмпирические константы в формулах (2)-(3) были найдены методом наименьших квадратов. В частности для модели ВВН1-3: P о = 6 кПа; P * = 70 кПа; Q * = 3,44 м³/мин; A о = 5,65 кВт; A i = -0,0111 кВт/кПа; B о = -2,57 м³/мин; B i = 0,531 м³/(минкПа); B 2 =-0,0176 м³/(мин-кПа²); B 3 =2,511^10 -4 м³/(мин^кПа³); B 4 = -2,511 •10⁶ м³/(мин^кПа⁴).

Первый этап - откачивание воздуха из ресивера. Как известно, в общем случае дифференциальное уравнение откачки вакуумным насо- сом воздуха из некоторой емкости имеет следующий вид [14]:

dP

V 2 •“;  =^{- P}2 • Q ( ^P2 ⁾⁺ S T ⁺ S ГВ ’     ⁽³⁾

dt где V2 - объем ресивера; P2 - давление; t - текущее время; Q(P) - зависимость эффективной производительности вакуумного насоса от давления в ресивере (см. формулу (2)); St - поток натекания, обусловленный утечками; S гв - поток газовыделения.

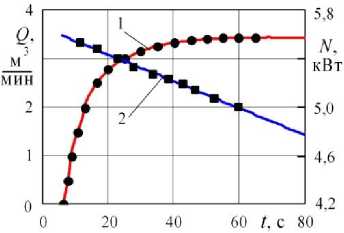
Рис. 2. Нагрузочные характеристики ВВН1-3 (точки – экспериментальные данные [17], линии - результаты расчета по формулам (1), (2))

В низковакуумных насосах, в т. ч. водокольцевых, потоком газовыделения пренебрегают. Для потока натекания используем обычно принимаемую в вакуумной технике гипотезу

S t = Г • QP a ) ■ ( P a - P ) . (4)

где Г - безразмерная эмпирическая константа, определяемая по величине P z , при которой давление в ресивере прекращает уменьшаться из-за натекания, т. е. выполняется равенство:

Г • QP a ) • ( P a - P z ) = P z ■ QP z ) ■    (5)

Из (5) следует

_Г =       Q ( k • P a )

1 — k   Q ( P a ) .

где k = P z I P a .

Подставляя (5) в (3), получим

V 2 • -P ² = Г • Q ( P a ) • P a - P 2 Q ( P 2 ) + Г • Q ( P a )) ■ dt

Результаты и их обсуждение. Для первого этапа работы установки математическая постановка задачи Коши включает дифференциальное уравнение (7) с начальным условием P(0) = Pa. Ее решение было найдено численным методом. Результаты представлены на рисунке 3.

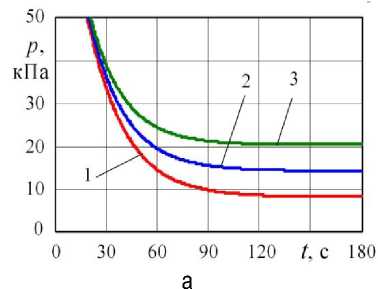
Рис. 3. Влияние натекания на первый газодинамический процесс при V 2 = 1,5 м³: 1 – k = 0,08; 2 – k = 0,14; 3 – k = 0,20; а – давление в ресивере, б – массовый расход газа

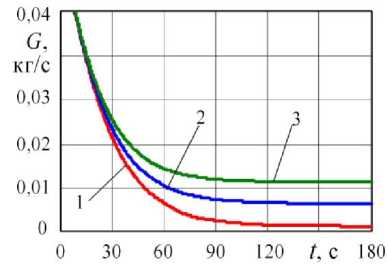
б

Как и в работах [16, 18], интенсивность натекания (утечек) заметно влияет на процесс откачивания воздуха. По рисунку 3 видно, как с увеличением k снижается уровень вакуума, который может быть достигнут. При этом уменьшается время его достижения. Наибольший вакуум будет при давлении P z .

Второй этап начинается после открытия крана 5 на рисунке 1. Газ из вакуумной камеры по трубопроводу начинает поступать в ресивер. При дозвуковом течении в трубе постоянного диаметра массовый расход газовой смеси зависит от давления на входе P i и на выходе P 2 . Он может быть рассчитан по известной формуле Г.Н. Абрамовича [19] :

G = S •

( P( Y + 1 )/ Y ( ^  1 , P 1 --+ -tn -1 1 2 D  Y   P 2 J

- 2(^+1^^ Y • RT P P 1( 1 - Y )/ Y Y + 1

где L, D - длина и внутренний диаметр трубы соответственно; y - показатель адиабаты газа; А - коэффициент гидравлических потерь по длине трубы; Ri - газовая постоянная; Ti - тер- модинамическая температура в вакуумной камере; S = nD 2I4 - площадь поперечного сечения трубопровода.

Коэффициент гидравлических потерь на трение можно рассчитать по известной формуле Альтшуля:

( Л  68 У ⁰²⁵ _ D ■ р • W

X = 0,11 ■! — + — I , Re = —----, (9) D Re          μ где Re - число Рейнольдса; △ - абсолютная эквивалентная шероховатость стенки трубы; р -плотность газа; р - коэффициент динамической вязкости газа; W = G/(р S) - скорость течения.

Прежде чем продолжать расчет, необходимо убедиться, что число Маха на выходе из трубо- провода не превышает единицу (a - скорость звука):

M = W/a <  1 , a = Y RT , (10)

Если условие (10) не выполняется, то рассчитывать массовый расход газа в трубе следует не по формуле (8), а по скорости звука: G = р^ aS .

Математическая постановка задачи процесса выравнивания давлений включает два дифференциальных уравнения и начальные условия к ним:

dm¹ = - G + 0 , dm² = G , m i (0) = m 10 , m 2 (0) = m 20 , dt            dt

где m 1 , m 2 - масса газа в вакуумной камере и в ресивере в некоторый момент времени второго этапа соответственно; 0 - интенсивность испарения пищевых продуктов, кг/с.

Массу газа в вакуумной камере и в ресивере в начале второго этапа рассчитаем по уравнению состояния:

m 10 = P 10 V 1 /( R 1 T 10 ), m 20 = P 20 V 2 /( R 2 T 20 ). (12)

Если G << 0, то в первом приближении можно в первом уравнении (11) положить 0 » 0. Тогда задача Коши ( 11 ) упростится:

dm2 = G, m 2(0) = m 20, m 1 = m 0 - m 2, (13) dt где m 0 = m 10 + m 20.

Решение (13) найдено численным методом при L = 3 м и начальных давлениях P 1 = P_a , P 2 = 0,1 P a . Результаты расчетов представлены на рисунках 4-6.

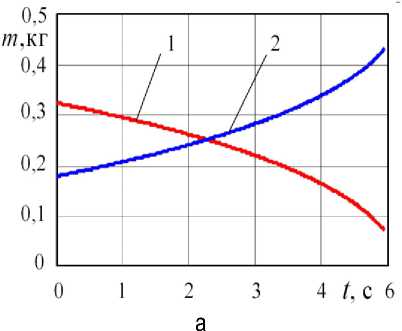
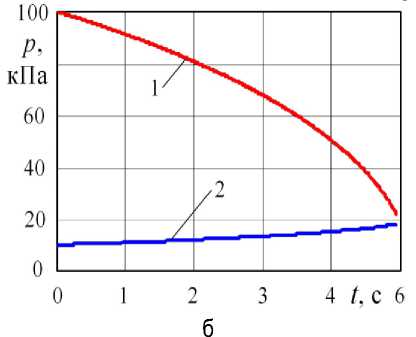
Рис. 4. Газодинамика на втором этапе при V 1 = 0,3 м³, V 2 = 1,5 м³, D = 25 мм, L = 3 м; а – масса газа в камере (1) и в ресивере (2); б – давление в камере (1) и в ресивере (2)

По рисунку 4 процесс выравнивания давлений является нелинейным даже при сделанных упрощающих предположениях. Темп изменений к завершению процесса увеличивается. В рассматриваемых условиях конечное абсолютное давление получилось около 20 кПа.

По рисунку 5 увеличение диаметра трубопровода приводит к ускорению процесса выравнивания давлений, но на конечное значение давления не влияет.

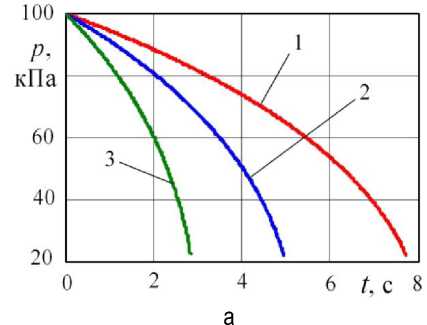
Рис. 5. Влияние диаметра трубопровода на газодинамику при V 1 = 0,3 м³, V 2 = 1,5 м³:

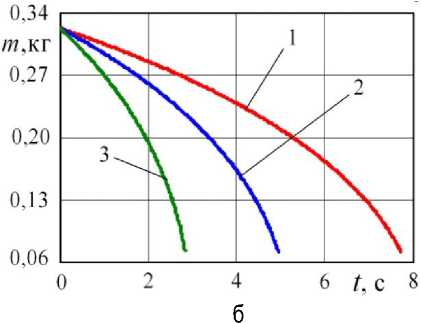
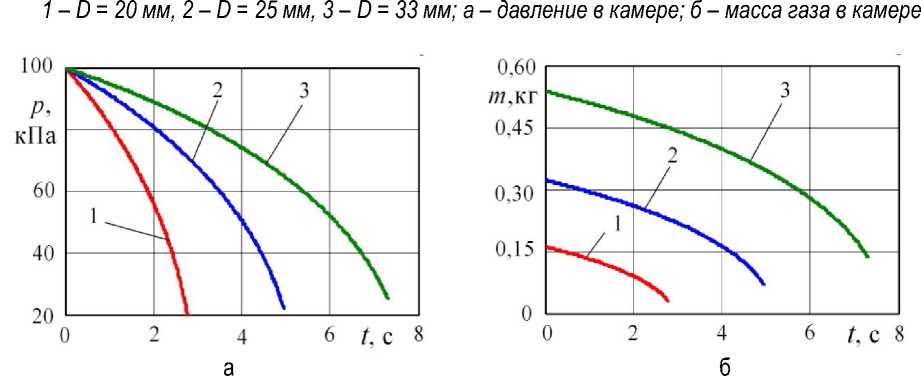
Рис. 6. Влияние объема вакуумной камеры V 1 на газодинамику при объеме ресивера V 2 = 1,5 м³, D = 25 мм, L = 3 м: 1 – V 1 = 0,15 м³, 2 – V 1 = 0,3 м³, 3 – V 1 = 0,5 м³; а – давление в камере;

б – масса газа в камере

По рисунку 6 увеличение объема вакуумной камеры (при неизменном объеме ресивера) приводит к росту времени выравнивания давлений. При этом происходит небольшое увеличение конечного давления и более заметное увеличение массы газа в камере.

Заключение. Исследовано влияние утечек на зависимости давление в ресивере и массового расхода газа от времени при заданном объеме ресивера. При возрастании интенсивность натекания (утечек) от 0,08 до 0,2 давление уменьшается от 20 до 9 кПа. Это свидетельствует о заметном влиянии утечек на процесс откачивания воздуха. Видно, как с увеличением интенсивность натекания снижается уровень вакуума, который может быть достигнут. При этом уменьшается время его достижения. Аналогично снижается и массовый расход при возрастании интенсивность натекания. При увеличении объема вакуумной камеры время дости- жения заданного давления увеличивается, а при увеличении диаметра трубопровода это же время уменьшается.

Представляется целесообразным в дальнейшем для усовершенствования предложенной модели учесть влияние температуры и влажности воздуха на рабочие характеристики водокольцевых вакуумных насосов, а также интенсивность испарения различных пищевых продуктов Θ.