Generalization of the Ostrowski inequalities on time scales
Автор: Khan A.R., Mehmood F., Shaikh M.A.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.25, 2023 года.
Бесплатный доступ
The idea of time scales calculus’ theory was initiated and introduced by Hilger (1988) in his PhD thesis order to unify discret and continuous analysis and to expend the discrete and continous theories to cases ``in between''. Since then, mathematical research in this field has exceeded more than 1000 publications and a lot of applications in the fields of science, i.e., operations research, economics, physics, engineering, statistics, finance and biology. Ostrowski proved an inequality to estimate the absolute deviation of a differentiable function from its integral mean. This result was obtained by applying the Montgomery identity. In the present paper we derive a generalization of the Montgomery identity to the various time scale versions such as discrete case, continuous case and the case of quantum calculus, by obtaining this generalization of Montgomery identity we would prove our results about the generalization of the Ostrowski inequalities (without weighted case) to the several time scales such as discrete case, continuous case and the case of quantum calculus and recapture the several published results of different authors of various papers and thus unify corresponding discrete version and continuous version. Similarly we would also derive our results about the generalization of the Ostrowski inequalities (weighted case) to the different time scales such as discrete case and continuous case and recapture the different published results of several authors of various papers and thus unify corresponding discrete version and continuous version. Moreover, we would use our obtained results (without weighted case) to the case of quantum calculus.
The ostrowski inequality, the holder inequality, the montgomery identity, time scales, quantum calculus
Короткий адрес: https://sciup.org/143180474
IDR: 143180474 | УДК: 517.51 | DOI: 10.46698/q4172-3323-1923-j
Текст научной статьи Generalization of the Ostrowski inequalities on time scales
Ostrowski proved an inequality to estimate the absolute deviation of a differentiable function from its integral mean. The below inequality is called the Ostrowski inequality which is extracted from [1]. For more study about the Ostrowski inequality, we refer to [2–7].
ℓ g^) - [ g(T) dT ^ sup |g‘(^)|(l - K)
1 - K J K<6<1
κ
1 (6 - K+l ) 2
4 + (I — к) 2
(1.1)
holds and this result had obtained by applying the Montgomery identity [8]. These properties would be derived for general time scales, which recapture discrete, continuous and many other cases. The pattern of current paper is consist of four sections. In the Section 1 and 2, we would present some preliminaries about time scales that are needed in the remainder of the paper. In the Section 3, we would get time scales versions of the generalized Montgomery identity and of the generalized Ostrowski inequality. While in the section 4 we would give several weighted time scales of the Ostrowski inequality. Throughout, we use our established results for the especial cases of discrete, continuous and quantum time scale. In the Section 5, we would give conclusion of the paper.
2. Time Scales Essentials
The idea of time scales calculus’ theory was initiated and introduced by Hilger (1988) in his PhD thesis [9] (supervized by Aulbach) in order to unify discret and continuous analysis and to expend the discrete and continous theories to cases “in between”. Since then, mathematical research in this field has exceeded more than 1000 publications and a lot of applications in the fields of science, i. e., operations research, economics, physics, engineering, statistics, finance and biology [10]. Even the time scale calculus theory may be used in most of the branches of science in which dynamic processes are explained by discrete-time/continuous-time models. We prefer the researcher to the book [11] written by Bohner and Peterson about the introduction to the singled variable time scale calculus and its implementations.
In 2004, Bohner introduced the variations’ calculus on time scale, he used the delta derivative and delta integral [12], and it has since then been further developed by several different authors in several different publications (see [13–18]). Many classical results of calculus of variations as necessary or sufficient conditions of optimality have been generalised to arbitrary time scale.
Definition 2.1. A time scale is an arbitrary nonempty closed subset of the real numbers. The most important examples of time scales are R, Z and q N 0 := {q l ll E N o } .
Definition 2.2. If T is a time scale, then we define the forward jump operator ст : T ^ T by ст(6) : = inf { t E T | t > 6} for all 6 E T, the backward jump operator p : T ^ T by p(6") := sup { T E T | t < 6} for all 6 E T, and the graininess function у : T ^ [0, to) by у(6) := ст(6) — 6 for all 6 E T. Furthermore for a function g : T ^ R, we define g " (6) = д(ст(6)) for all 6 E T and g p (6) = g(p(6)) for all 6 E T. In this definition we use inf 0 = supT (i. e., p(6) = 6 if 6 is the maximum of T) and sup 0 = inf T (i. e., p(6) = 6 if 6 is the minimum of T).
These definitions allow us to characterize every point in a time scale as following classifcation of points:
-
(i) 6 right-scattered = ^ 6 < ст(6),
-
(ii) 6 right-dense = ^ 6 = ст(6),
-
(iii) 6 left-scattered = ^ p(6) < 6,
-
(iv) 6 left-dense = ^ p(6) = 6,
-
(v) 6 isolated = ^ p(6) < 6 < ст(6),
-
(vi) 6 dense = ^ p(6) = 6 = ст(6).
Definition 2.3. A function g : T ^ R is called rd-continuous (denoted by C rd ) if it is continuous at right-dense points of T and its left-sided limits exist (finite) at left-dense points of T.
Theorem 2.1 (existence of antiderivatives) . Let g be rd-continuous. Then g has an antiderivative G satisfying G ^ = g.
<1 See Theorem 1.74 of paper [11]. >
Definition 2.4. If g is rd-continuous and θ 0 ∈ T, then we define the integral
θ
G(9) = j g(s)As
θ 0
for
θ ∈ T .
(2.1)
Therefore for g E C rd we have J 1 g(s)As = G(l) - G ( k ) , where G ^ = g. Theorem 2.2. Let g, h be rd-continuous, κ, ℓ, l ∈ T and α, β ∈ R . Then ( i ) J^M9) + WW = a J " 1 g ( 9 )A 9 + e J" 1 h ( 9 )A 9, (ii) fl g(9)A9 = - JK g(9)A9, (iii) J I g(9)A9 = £ g(9)A9 + // g^AQ, (iv) flg(9)h ^ (9)A9 = (gh)(l) - (gh)(K - flg ^ (9)h(a(9f)A9, (v) f f g(9)A9 = 0.
< See Theorem 1.77 of paper [11]. >
Definition 2.5. Let hc, fc : T2 ^ R, c E No, be defined by ho(9,T) = fo(9,T) = 1 (Vт,в E T)
and then recursively by
θ hc+i(9,T) = j hc(a(s),T)As (Vt, 9 E T)
τ
and
θ fc+i(9,T) = j fc(s,T)As (Vt,9 E T).
τ
Theorem 2.3 (Holder’s inequality) . Let к, I E T and g, h : [к, I] ^ R be rd-continuous. Then
ℓ j |g(9)h(9)|A9 ^
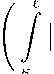
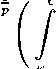
| h(9)
i q A9^ q ,
(2 . 2)
where 1 < p and p + q = 1 .
< See Theorem 6.13 of [11]. >
In 2008, Bohner et. al. proved the Ostrowski inequalities on time scales and they obtained unified and extended results to the literature and they also gave results to the quantum calculus case. In the current paper, we would obtain generalization of the Ostrowski inequalities on time scales and recapture the results of [19] for discrete and continuous versions and also recapture some results of papers [1, 8, 11, 20–22]. Moreover, we will use our parametric results to the case of quantum calculus.
3. Generalization of the Ostrowski Inequality on Time Scales
To prove the our main Theorem 3.1, we require the below generalized Montgomery identity.
Lemma 3.1 (the generalized Montgomery identity) . Let к,1,т,9 E T , к < I and g : [к, l] ^ R be differentiable and parameter A E [0,1] . Then
ℓℓ
(1 — A ) g ( 9 ) + | (g(K) + g(1)) = [ g^ ( т )А т + [p(9,т ^( т )А т, (3.1)
2 I — kJ I — kJ
κκ where
Р(9,т ) = <
-
τ -
(к + ' ),
(I — )■
к C т < 9,
9 C т C I.
<1 Applying Theorem 2.2 (iv) we have
θθ
/ (т — ( k +A~ r~ ))g Л ( т )А т = (9 — ( k +A~ r~ ))g ( 9 )+A~ т~ д ( к ) — / g" ( 9 )А т- κκ
ℓℓ j (т — (l — A^Ж(т)Ат = —(9 — (l — A1—-^))g(9) + A1^g(l) — / g"(9)Ат. θθ
Therefore
ℓℓ ℓ
[ g^( т )А т + [р( 9,т )g Л ( т )А т = [ g^( т )А т + ( l — k)(1 — A ) g ( 9 )
ℓ - κ ℓ - κ ℓ - κ ℓ - κ
κκ κ
ℓ
+ A ^2— ( g ( K ) + g ( l )) — j g " ( т )А т
κ
= (1 — A)g(9) + 2(g(K)+ g(l)),
as we just require 1 C a C n , 0 C b C n — 1 .
Remark 3.2. If we put A = 0 in Corollary 3.1, then we recapture Corollary 3.2 of paper [19] and Theorem 2.1 of paper [20].
Continuous Case:
Corollary 3.2. We let T = R . Then
ℓℓ
(1 — A )g( 9 ) + A (g(K) + g(1)) = [ д( т ) dT + —^— [ p( 9,т) g ‘ ( т) dr.
2 I — kJ I — kJ
κκ
Remark 3.3. If we put A = 0 in Corollary 3.2, then we recapture the Montgomery identity in the continuous case which may be seen in [8, p. 565] and Theorem 2.1 of paper [20].
Quantum Calculus Case:
Corollary 3.3. We let T = q N 0 , q> 1 , к = q m , I = q n and т = q c with m < n. Then
. n —1 n —1
(1—A)g(»)+2 (g(qn)+»Г‘)) = -n—m E g(qc+1)+E g q—g(qc )]p(», qc), 4 4 c=m c=m where
p(9,q c ) = <
q c
-
q c
-
nm qm + A»-—- ), (q n — 2q),
q m ^ q c < 9,
9 ^ q c ^ q n .
b =0
p(a, b) =
b
-
λn
b
-
2, Ч1 — 2)-
0 < b < a — 1, a C b ^ n — 1.
Remark 3.4. If we put A = 0 in Corollary 3.3, then we recapture Corollary 3.4 of [19].
Theorem 3.1 (the generalized Ostrowski inequality) . Let κ,ℓ,τ,θ ∈ T , κ < ℓ and g : [к, I] ^ R be differentiable and parameter A € [0,1] . Then
ℓ
(1 — A)g(9) + A (g(K) + g(f)) — [g" (т)Ат
< — ^(9,*) + f 2 (9,l)),
(3.2)
2 I — kJ
κ where
M = sup \g ^ (9)\. κ<θ<ℓ
This inequality is sharp in the sense that the right-hand side of (3.2) cannot be replaced by a smaller one.
<1 Using Lemma 3.1 with р(9,т ), we have
ℓ
ℓ
[ Р(9,т )g A (т )Ат ℓ - κ
κ
(1 — A)g(9) + A (g(K) + g(l)) — ^ [g - (т)Дт
2 I — kJ
κ
<
M ℓ - κ
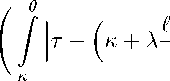
^ Ат + J | т — ^l
κ
-
ℓ
-
θ
A^—^ )^т)
M
ℓ
-
θℓ
/ (т — ( k + A^)) А т + / ((' — A^) — т) А т κθ
= ^---- (f 2 (9,к)+ f 2 (9,l)). ▻
ℓ - κ
Remark 3.5. If we put A = 0 in Theorem 3.1, then we recapture Theorem 3.5 of [19] and which is stated in the following as:
Corollary 3.4. Suppose the assumptions of Theorem 3.1 is true. Then
<
M
θ
ℓ
-
κ
κ
g(^)
τ
-
-
ℓ
-
κ
к | Ат +
ℓ
j g" (t)At
κ
ℓ
θ
M
ℓ
-
κ
ℓ
ℓ
-
κ
j p(9,T )дл (т )A t
κ
θ
κ
(t — к)Ат +
MW f 2 (9,1))
ℓ
j(i - т )AtJ θ
(3.3)
Note that, since p(9, к) = 0, the smallest value attaining the supremum in M is greater than к. To prove the sharpness of inequality (3.3), let g(9") = 9, к = T, I = T2 and 9 = T2.
It follows that д л (9) = 1 and M
= 1. Beginning with the left-hand side of (3.2), we have
T 2
-
g(9)
-
ℓ
T 2
T 2 - T 1
ℓ
-
-
κ
j gCT ( t )A t = T 2
κ
-
T 2
T 2 - T 1
У ст(т )Ат
T 1
T 2
T 2
-
T 1
T 1
T 1
У (т 2 ) л At
T 2
-
T 1
1TAt
T 1
-
T i +
T 2
-
T 1
T 2
1T А
T 1
Beginning with the right-hand side of (3.2), we have
M
ℓ
-
κ
(f 2 (9,к)+ f 2 (9,l)) =
T 2 - T 1
T 2 T 2
I У (т — Т 1 )Ат — У (т — T 2 )A t j
T 1 T 1
T 2
T 2 - T 1
(
T 2
-
T 1 T 2 + t 2 +
1тAt
T 1
=
— T i +
T 2
T 2 - T 1
1 т А т
T 1
Therefore in this particular
case
g(9)
-
ℓ
ℓ
-
κ
j g" (t)At
κ
>
M
ℓ
-
κ
(f 2 (9,K)+ f 2 (9,l))
and by (3.2) also
g(9)
-
ℓ
-
κ
ℓ
j g" (t)At
κ
<
M
ℓ
-
κ
(f 2 (9,K)+ f 2 (9,l)).
So the sharpness of the Ostrowski inequality is shown.
The following are the different cases of the generalized Ostrowski inequality with A = 0. Discrete Case:
Corollary 3.5. We suppose T = Z. Let к = 0, I = n, t = b, 9 = a and g(c) = yc. Then where
|
1 n У а - n^y b |
M |
n + 1 |
2 n 2 - 1 |
|
n |
a 2 |
1 4 |
|
|
b =1 |
M = max | Ay„ | .
1 -1 a
(3.4)
This is the discrete Ostrowski inequality (see Theorem 3.1 of [20]) , where the constant 1/4 in the right-hand side of (3.4) is the best possible in the sense that it cannot be replaced by a smaller one.
Continuous Case:
Corollary 3.6. We suppose T = R . Then
= M (I - к)
1 (9 — K+l ) 2
4 + (I - к) 2
ℓ
g ( 9 ) - т-к $gT )dT
κ where
M = sup \ g ‘ (9) | .
κ<θ<ℓ
This is the Ostrowski inequality in the continuous case [1], where again the constant 1/4 in the right-hand side is the best possible.
Quantum Calculus Case:
Corollary 3.7. We suppose T = q N 0 , q> 1, к = q m and I = q n with m < n. Then
g(9)
-
-------[ g" (t )At qn - qm qm
^ q n
M
- q m
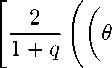
-
1+q (q m + q n )
+
- ( 1+qflqm + q n ) 2 + (2(1 + q) - 2)(q 2m + q 2n )
,
where
M = sup qm <θ g(q9)—_g(9) (q — 1)9 and 1/4 in the right-hand side is the best possible. Corollary 3.8. If put A = 1 in Theorem 3.1. Then we obtain following average trapezoid type inequality on time scale ℓ д(к) + g(l) - ^ / g"(t)At 2 I — к J κ < —~ (f2(9,к) + f2(9,l)), (3.5) where M = sup \gA(9)\. κ<θ<ℓ
4. The Weighted Case The below weighted Ostrowski inequality with parameter on time scale holds. Theorem 4.1. Suppose the assumptions of Theorem 3.1 is true and £ E T and q E Crd. Then A + (1 ℓ —A)g(0) —У q"(т)g"(t)At κ ^ ^ A + θ I q"(t)|(1 - A)g(0) κ ℓ A + (1— A) ( у |g(°) κℓ + ℓ —g"(t)|At + У q"(t)|(1 -W —g"(t)|At θ 1ℓ κ 1ℓ κκ A + sup q" (t )[h2(K,9) + h2(l, 0)], K^T<1 1 + 1 = 1, p> 1, pq (4.1) (4.2) g(^(l)) —gHK))+ (1 —a) (0) —gHKl+gHl)) 2 ' 2 where ℓ A = |(д(к) +g(l)), У q"(T)At = 1, q(T) > 0. κ <1 As from left side of (3.2) we have ℓ A (д(к) + g(l)) +(1 — A)g(9) — У q"(t)g"(t)At κ ℓ = 2(g(K)+ g(f))+ jq" (t )((1 — A)g(O) — g" (t ))At κ θℓ < A + У q" (t )|(1 — AW) — g" (t )|At + j q" (t )|(1 — A)g(0) — g" (t )|At and therefore (4.1) is shown. The first part of (4.2) can be done easily by applying Holder’s inequality. By factoring suPk θℓ A + У q" (t )|(1 - A)g(9) - g" (t )|At + j q" (t )|(1 - X)g(9) - g" (t )|At κ θ ^ A + sup q" (t) K^T<1 ' / (g" (t ) - (1 - Л)д(9))Ат + У ((1 - A)g(9) - g" (t )}At) = A + sup q" (t) K^T<1 ' У ((1 - A)g(9) - g" (t )}At + У ((1 - A)g(9) - g" (t )}At) = A + sup q"(t) [h2(K, 9) + h2(l, 9)] K^T<1 and therefore the 2nd part of (4.2) holds. Finally for deriving the 3rd inequality, we implement the fact that suP {\д(^(т)) - (1 - АЫ9)|} = max {g(a(l)) - (1 - A)g(9), (1 - A)g(9) - д(ст(к)^ K^T<1 = дИ1)) -дИк))+ (1 - Л) (9) - дИк)) + дИ1)) 2 ' 2 Thus (4.2) is shown. > Remark 4.1. If we put q"(t) = i—k in Theorem 4.1 then obtain the result without weights. Remark 4.2. If we put q"(t) = i—k and A = 0 in Theorem 4.1 then we recapture the Theorem 3.1 of [19]. Remark 4.3. Theorem 4.1 with A = 0 states a similar result as shown in Theorem 3.1 of [21], if we consider the normalized isotonic functional B(g) = jf q"(t)g"(t)At. Remark 4.4. The second inequality of (4.2) with A = 0 is comparable to the achievement in Theorem 3.1 of [22] for the continuous case (see Corollary 3.3 of [22]). Discrete Case: Corollary 4.1. We suppose T = Z. Let к = 0, I = n, t = b, 9 = a, £ = c and g(c) = yc. Then En=1qa = 1, 0 ^ qa, and n A + (1 - A)ya - ^^ qbyb b=1 nn ^ A + (1 - A) ^ qb|ytt| + ^ qb\yb\ b=1 b=1 n pn q n pn q a + (1 - A) (^E WpJ (E qqb) + (E\yb\p) (E qqb) , p + q = 1, p> 1, ^ A + maxb=1 ,n q(b) ( bE Уь^ , yn-y0 + (1 - A)ytt- y0^ where A = 2(yo + yn). Remark 4.5. If we put A = 0 in Corollary 4.1 then we recapture the Theorem 4.1 of [20] and Corollary 4.3 of [19]. Continuous Case: Corollary 4.2. We suppose T = R. Then j"1q(т)dт = 1, 0 < q(т) and A + (1 ℓ - X)g(9) - j q(тMt ) dт к θℓ < A + jq(T)|(1- ХМ9) -g(T)|dт +jq(т)|(1 - X)g(9)- д(т)\ dr < ℓ A + (1 - X)[ / ℓ + 1ℓ x к 1ℓ к 1 + 1 = 1, p> 1, pq A + sup q(т) [h2(K,9) + h2(l,9), K<T<1 ^ ^ + (1 — X)g(9) - g(K)+■ 2 ' 2 where ℓ A = |(s(k) +g(l)), j q(T) dT = 1, q(T) > 0. Remark 4.6. If we put X = 0 in Corollary 4.2 then we recapture the Corollary 4.4 of [19]. Corollary 4.3. If we put X = 1 in Theorem 3.1. Then we obtain following average trapezoid type inequality with weights on time scale < s(k) + g(l) s(k) + g(l) + s(k) + g(l) + ℓ - j qa (т )gCT (т )Ат к ℓ К |pАт <s(k) +g(l) 1ℓ 7 x к ℓ sup qCT(т) / K<T<1 \ J ℓ + j qa (т )|gCT(т )|Ат 1 + 1 = 1, p> 1, pq _ g(^(l))- Another interesting conclusion of Theorem 4.1 with q"(т) = i-1^ and X = 0 is the following corollary. Corollary 4.4. Suppose κ, ℓ, τ, θ ∈ T, κ < ℓ and g is differentiable. Then ℓ S(9) - [ S"(т)Ат ℓ-κ < 1-M (f2(9,K)+ f2(9,l)), (4.3) where M = sup \g^ (0)|. ct(k)<6<1 Note that this was shown in several ways in Theorem 3.1 In inequality (4.3) we implement the fact that the functions h2 and f2 satisfy h2(T, 9) = (—1)2f2(9,T), V9 G T, т G Tc(see Theorem 1.112 of [11]). Remark 4.7. Moreover note that there is a small difference of (4.2) in comparison to Theorem 3.1, as we have supCT(K)<ginstead of supK
5. Conclusion In this paper, the generalized Ostrowski inequalities (with weights and without weights) are proved on time scales and thus our results unified and extended corresponding to discrete and continuous versions of previously proved results of different researchers in various papers [1, 8, 11, 19–22]. Moreover, we have used our obtained results to the quantum calculus case.
Список литературы Generalization of the Ostrowski inequalities on time scales
- Ostrowski, A. Uber die Absolutabweichung einer Differenzierbaren Funktion von Ihrem Integralmittelwert, Commentarii Mathematici Helvetici, 1937, vol. 10, no. 1, pp. 226-227. DOI: 10.1007/BF01214290.
- Hassan, A., Khan, A. R., Mehmood, F. and Khan, M. BF-Ostrowski Type Inequalities via 0-A-Convex Functions, International Journal of Computer Science and Network Security, 2021, vol. 21, no. 10, pp. 177-183. DOI: 10.22937/IJCSNS.2021.21.10.24.
- Hassan, A., Khan, A. R., Mehmood, F. and Khan, M. Fuzzy Ostrowski Type Inequalities via h-Convex, Journal of Mathematical and Computational Science, 2022, vol. 12, pp. 1-15. DOI: 10.28919/jmcs/6794.
- Hassan, A., Khan, A. R., Mehmood, F. and Khan, M. Fuzzy Ostrowski Type Inequalities via 0-A-Convex Functions, Journal of Mathematical and Computational Science, 2023, vol. 28, pp. 224-235. DOI: 10.22436/jmcs.028.03.02.
- Bohner, M., Khan, A. R., Khan, M., Mehmood, F. and Shaikh, M. A. Generalized Perturbed OstrowskiType Inequalities, Annales Universitatis Mariae Curie-Sklodowska, Sectio A — Mathematica, 2021, vol. 75, no. 2, pp. 13-29. DOI: 10.17951/a.2021.75.2.13-29.
- Dragomir, S. S., Khan, A. R., Khan, M., Mehmood, F. and Shaikh, M. A. A New Integral Version of Generalized Ostrowski-Griiss Type Inequality with Applications, Journal of King Saud University — Science, 2022, vol. 34, no. 5, pp. 1-6. DOI: 10.1016/j.jksus.2022.102057.
- Shaikh, M. A., Khan, A. R., and Mehmood, F. Estimates for Weighted Ostrowski-Griiss Type Inequalities with Applications, Analysis, 2022, vol. 42, no. 3, pp. 1-11. DOI: 10.1515/anly-2021-0044.
- MitrinoviC, D. S., PecariC, J. E. and Fink, A. M. Inequalities Involving Functions and their Integrals and Derivatives, Mathematics and its Applications (East European Series), vol. 53, Dordrecht, Kluwer Academic Publisher Group, 1991, 565 p. DOI: 10.1007/978-94-011-3562-7.
- Hilger, S. Ein Mafikettenkalkul mit Anwendung auf Zentrumsmannigfaltigkeiten, Ph.D. Thesis, Uni-versitat Wurzburg, 1988.
- Bohner, M. and Georgiev, S. G. Multivariable Dynamic Calculus on Time Scales, Springer International Publishing, 2016. DOI: 10.1007/978-3-319-47620-9.
- Bohner, M. and Peterson, A. Dynamic Equations on Time Scales, Boston, MA, Birkhaiuser Boston Inc., 2001. DOI: 10.1007/978-1-4612-0201-1.
- Bohner, M. Calculus of Variations On Time Scales, Dynamic Systems and Applications, 2004, vol. 13, no. 3-4, pp. 339-349.
- Bartosiewicz, Z., Martins, N. and Torres, D. F. M. The Second Euler-Lagrange Equation of Variational Calculus on Time Scales, European Journal of Control, 2011, vol. 17, no. 1, pp. 9-18. DOI: 10.3166/ejc.17.9-18.
- Ferreira, R. A. C., Malinowska, A. B. and Torres, D. F. M. Optimality Conditions for the Calculus of Variations with Higher-Order Delta Derivatives, Applied Mathematics Letters, 2011, vol. 24, no. 1, pp. 87-92. DOI: 10.1016/j.aml.2010.08.023.
- Hilscher, R. and Zeidan, V. Calculus of Variations on Time Scales: Weak Local Piecewise C^ Solutions with Variable Endpoints, Journal of Mathematical Analysis and Applications, 2004, vol. 289, no. 1, pp. 143-166. DOI: 10.1016/j.jmaa.2003.09.031.
- Hilscher, R. and Zeidan, V. Weak Maximum Principle and Accessory Problem for Control Problems on Time Scales, Nonlinear Analysis: Theory, Methods and Applications, 2009, vol. 70, no. 9, pp. 3209-3226. DOI: 10.1016/j.na.2008.04.025.
- Malinowska, A. B., Martins, N. and Torres, D. F. M. Transversality Conditions for Infinite Horizon Variational Problems on Time Scales, Optimization Letters, 2011, vol. 5, no. 1, pp. 41-53. DOI: 10.1007/s11590-010-0189-7.
- Malinowska, A. B. and Torres, D. F. M. Natural Boundary Conditions in the Calculus of Variations, Mathematical Methods in the Applied Sciences, 2010, vol. 33, no. 14, pp. 1712-1722. DOI: 10.1002/mma.1289.
- Bohner, M. and Matthews, T. Ostrowski Inequalities on Time Scales, Journal of Inequalities in Pure and Applied Mathematics, 2008, vol. 9, no. 1, pp. 1-8.
- Dragomir, S. S. The Discrete Version of Ostrowski's Inequality in Normed Linear Spaces, Journal of Inequalities in Pure and Applied Mathematics, 2002, vol. 3, no. 1, art. 2.
- Dragomir, S. S. Ostrowski Type Inequalities for Isotonic Linear Functionals, Journal of Inequalities in Pure and Applied Mathematics, 2002, vol. 3, no. 5, art. 68.
- Gavrea, B. and Gavrea, I. Ostrowski Type Inequalities from a Linear Functional Point of View, Journal of Inequalities in Pure and Applied Mathematics, 2000, vol. 1, no. 2, art. 11.


