Геодинамические индикаторы для поиска нефтегазоносных полей

На сегодняшний день в мире открыто около 10 тыс. месторождений нефти и газа [2; 4; 5; 7; 12; 16; 18; 25]. Из них в Российской Федерации находится около полутора тысяч нефтяных и четырехсот газовых [2; 4; 5; 7; 12].

В промышленных масштабах нефть обнаружена и добывается в 65 странах мира. Кроме России, наиболее богатыми на запасы черного золота являются Саудовская Аравия, США, Ирак, Ливия, Иран, Венесуэла, Объединенные Арабские Эмираты, Канада. От них не отстают Алжир, Нигерия, Катар, Аргентина, Мексика, Индия [2; 5; 12; 16].

Поиск и разведка нефтяных и газовых месторождений в последние несколько лет достигли больших успехов. Сегодня исследован примерно 1% всей суши Земли на глубинах порядка 2–3 километров [4; 7; 13; 16; 17; 23]. Активно ведется поиск морских месторождений [5; 12].

Как известно, существуют следующие методы поиска нефтегазоносных бассейнов: геологический, геофизический, гидрогеохимический, бурение и исследование разведочных скважин [2; 7; 12; 16–18; 23; 25].

Успех применения того или иного из указанных методов зависит от ряда факторов, например, таких как сложность геологического строения района, глубина залегания и мощность залежи, информация о физико-механических свойствах и агрегатном состоянии горных пород, наличие достоверных данных о геофизических полях и многих других данных [2; 7; 12; 16–18; 23; 25].

Ведущим геофизическим методом поиска нефтегазовых месторождений является сейсморазведка, на которую тратится более двух третей капиталовложений, выделяемых на геофизические работы [2; 4; 7; 12; 23]. Если же говорить о ряде районов Восточной Сибири, Казахстана и Средней Азии, где сейсмогеологические условия крайне неблагоприятны, сейсморазведку применяют в комплексе с гравиразведкой и электромагнитным зондированием [13; 17; 18; 23; 25; 29].

В настоящей статье не ставится цель выполнить исчерпывающий анализ методов поиска нефтегазовых месторождений – о преимуществах и недостатках того или иного метода написано и сказано уже немало в перечисленных литературных источниках. Наша задача – обосновать принципиально новый индикатор, позволяющий по косвенным измеримым либо вычисляемым признакам идентифицировать тот или иной район как нефтегазоносный.

Многочисленными исследованиями установлено, что динамические изменения, происходящие в литосфере Земли, есть следствие протекания в ней различных гео-деформационных процессов. Такие процессы, генетически связанные с опасными геодинамическими явлениями, принято подразделять на «быструю» составляющую – сейсмические процессы (землетрясения) и «медленную» составляющую – современные движения отдельных слоев и блоков земной коры [8; 14; 15; 26; 30].

Искать геодинамический индикатор наличия нефтегазоносных бассейнов в «быстрой» составляющей не имеет смысла, поскольку исследования многих авторов однозначно говорят о том, что никакой пространственной связи между нефтегазоносными бассейнами и распределением эпицентров землетрясений в верхних слоях земной коры (а нас интересуют именно верхние слои земной коры, где залежи нефти и газа фиксируются в диапазоне глубин до 4 км) не прослеживается (рис. 1).

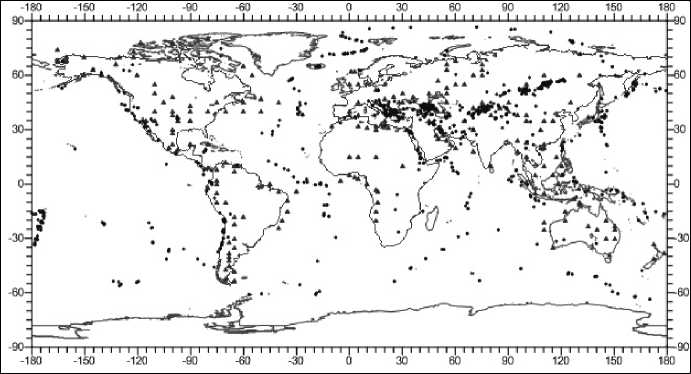
Рис. 1. Совместное распределение нефтегазоносных месторождений (обозначены треугольниками) и эпицентров землетрясений (обозначены точками), произошедших в период с 115 по 2014 г. на глубинах до 4 км

Следовательно, искать нужно среди параметров, характеризующих «медленную» составляющую, исследуя те из них, которые определяют особенности современных движений верхних слоев земной коры. А для этого необходимо знать распределение геодинамических напряжений и смещений в земной коре на упомянутых выше глубинах.

При этом на начальном этапе возник резонный вопрос: какой моделью пользоваться – упругой или упруго-вязкой? Для ответа на него авторами выполнены численные оценки распределения вязкости на интересующих нас глубинных уровнях.

Расчеты производились в соответствии с моделью изменения вязкости η( z ) с глубиной [10], а именно:

[ T ( z )] 0^{857      f}    2.5 p ( z ) gz   )

10      p (X ( z ) + 2/3 p ( z ) )

= Ak (z)exp где ρ(z) – плотность вещества земной коры; λ(z) – упругий модуль Ламе; μ(z) – модуль сдвига, характеризующие прочностные свойства литосферы; T(z) – температура вещества земной коры; g – ускорение свободного падения; z – глубина; Ak(z) – коэффициент пропорциональности.

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Как следует из соотношения (1), все входящие в него переменные величины являются функциями от глубины z . Поэтому в нашем исследовании была проведена весьма объемная работа по численным оценкам указанных величин на интересующих нас глубинных уровнях.

Данные по распределению плотности вещества земной коры ρ(z) (рис. 2) заимствованы из созданной в 2013 году модели земной коры CRUST 1.0, представляющей собой 9-уровневую модель с осреднением по сетке 1°х1° edu/~gabi/, распределения упругих модулей λ(z) (рис. 3) и μ(z) (рис. 4) рас- считывались в соответствии со следующими соотношениями:

ц ( x , у , z ) = р ( x , у , z )V 2 ( x , у , z ),

X(x, у, z) = p(x, у, z) (Vp(x, у, z) - 2Vs2(x, у, z)), где Vp и Vs – скорости продольных и поперечных сейсмических волн соответственно, которые также взяты из модели земной коры CRUST 1.0.

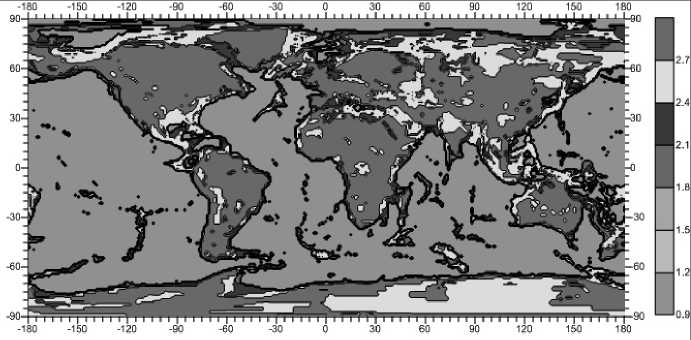
Рис. 2. Распределение плотности вещества земной коры на глубине 3 км, г/см³

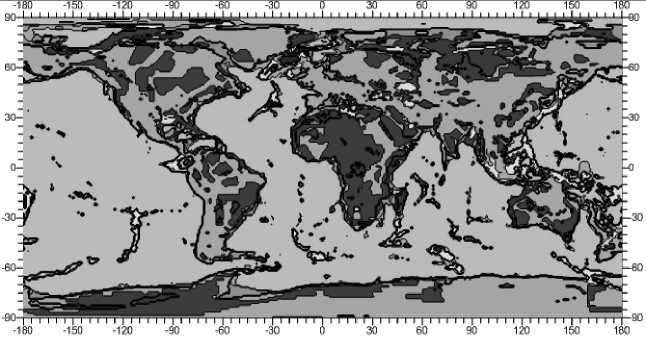
Рис. 3. Распределение упругого модуля Ламе λ × 10¹⁰ Па на глубине 3 км

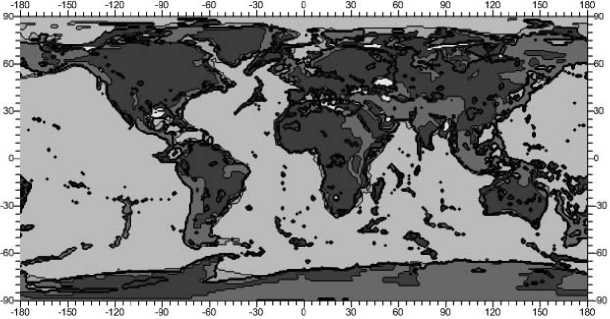
Рис. 4. Распределение модуля сдвига μ × 10¹⁰ Па на глубине 3 км

Распределение температуры в земной коре рассчитывалось по двум различным моделям – отдельно для континентальной части литосферы и отдельно – для океанической [8; 26; 30].

Так, для континентальной части литосферы температура определялась в соответствии с предложенной авторами моделью [10]:

T ( z ) = CA- ^ D ^:   + C ln( a + bz ) + C 3 ,                (3)

a n ~ 0    n + 1 b

1                                                f ^{( n} ) ( z _n)

где A 0 - константа, равная 3 • 10^-6 Вт/м³; a = —, H - толщина литосферы; D_n = -—;

-

( k_n - k„ )                      ^{H                                    n} !

a = k ; b = - -      ; k k - коэффициенты теплопроводности на дневной поверх-

0          H 0H ности и на границе «литосфера – литосферная мантия» соответственно; z – глубина.

Все это позволило выполнить расчет распределения температуры в земной коре на интересующих глубинных уровнях. Для примера на рис. 5 приведено распределение температуры на глубине 3 км.

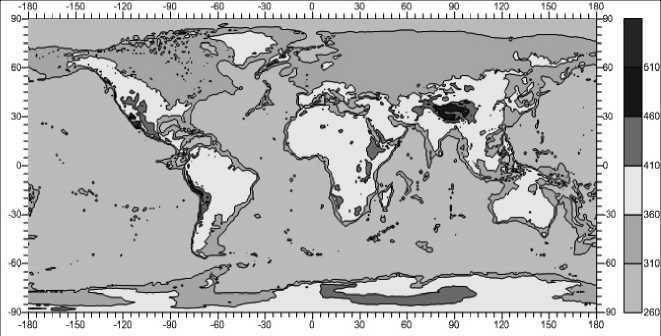
Рис. 5. Распределение температуры на глубине 3 км, K

Величины D_n из (3) находились в соответствии с рекуррентным выражением, обоснованным авторами [10]:

f ⁽ n ) ( z ) =

( - 1) n e -°² ( a + bz ) n ^{+ 1}

< a n ( a + bz ) n + nb

×

×

n-1                                      m an-1 (a + bz)n-1 + У an-(m+1)bm (a + bz)n-(m+1) П (n — k) m=1                                     k=1

Коэффициенты C ₁, C ₂, C ₃ вычислялись следующим образом:

^( T h - T o )

Ci =

a aQ 0 in a + bH bk ₀        a

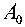
Y Dn

n = 0

H n ^{+ 1}

n + 1

1₁ a + bH ln

C = aQ o _- A o C

2     k 0      a ¹

ln a

—

C2, b где T0, Q0, k0 – температура, тепловой поток и коэффициент теплопроводности на дневной поверхности, а TH – температура на границе литосфера – литосферная мантия.

Распределение температуры в океанической части литосферы рассчитывалось в зависимости от ее возраста в рамках модели остывающего полупространства [26;

• 30]    в соответствии с соотношением

T ⁽ z ) - T ⁰ = erf [ z-^

T -J э ГУТ* h ²o        V ^ZV ^x t 7

где T_H – температура на границе литосфера – литосферная мантия (принималась равной 1717.15 K ), x - коэффициент температуропроводности (принимался равным

10^–6 м²/с [26; 30], erf – функция ошибок, t – возраст литосферы.

Величины коэффициента A_k в зависимости от глубины z определялись исходя из следующей системы соотношений:

A ⁽²⁾ _— A ⁽¹⁾

если z <  H M , то ^Ak ⁽ z ) = A ™ + - |kl- ⁽ z ^— H o );

^HM ^H 0

A ⁽³) _— A (4)

если z >  H_M , то A ( z ) = A ^⁴⁾ + ^k---- k ---( z — H_M — H ).

^m              k              k                                                                1

H L ^— H M ^— H 1

В соотношениях (7) использованы следующие обозначения: H_M – глубина литосферы до границы Мохо; H_L – общая толщина литосферы до границы «литосфера – литосферная мантия»; H ₀ – глубина расположения океанического дна; H ₁ – глубинный уровень под Мохо (принимается на 1 км глубже самой границы Мохо).

Величины коэффициентов A_k ⁽ⁱ⁾ определялись на основе имеющейся информации о величине вязкости на фиксированных глубинах z = z _фикс по крайней мере в четырех местах [26; 30]:

• 1)    на дневной поверхности (или на океаническом дне);

• 2)    на границе Мохо;

• 3)    непосредственно под границей Мохо;

• 4)    на границе литосфера – литосферная мантия.

В этих «точках» оценивались величины коэффициентов по формуле

A k ( z фико ) =

n ( z фико )

a ⁽ z фико

RT ^)

2,5 P ( z фико )

X ( z фико + 2 Ц ( z фико )/3

Приведем эквипотенциальное распределение величины вязкости, рассчитанное по формуле (1) с учетом соотношений (2)–(8) (рис. 6).

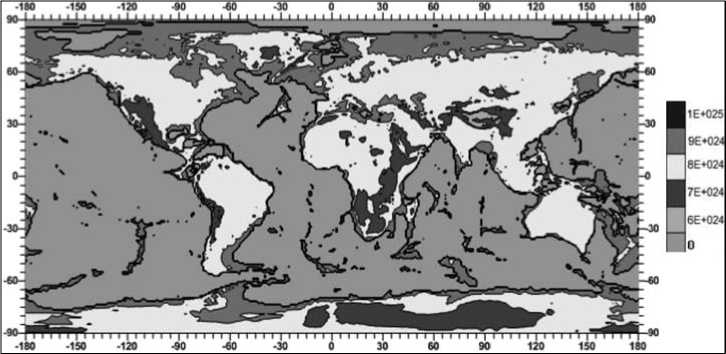
Рис. 6. Распределение вязкости на глубине 3 км, Па∙с

Видно, что величина вязкости значительна, изменяясь в пределах одного порядка, что говорит о нецелесообразности использования упруго-вязкой модели для верхних слоев земной коры на глубинах 1–4 км.

Поэтому мы применили упругую модель для расчета компонент тензора напряжений и составляющих вектора смещений в геологической среде для этих глубин. Рассмотрим эту модель.

Математическая модель оценки глобальных напряжений, смещений и деформаций в литосфере Земли

Основным фактором, влияющим на формирование и развитие геодинамических неустойчивостей, является гравитационное поле планеты [1; 20–23; 28; 29], поэтому для математической модели напряжений будем использовать аномальное гравитационное поле в изостатической редукции (рис. 7).

Если подходить к вопросу о построении математической модели напряженно-деформированного состояния литосферы в глобальном масштабе, то возникает необходимость в первую очередь в корректно рассчитанной характеристике, его отражающей, значения которой известны в указанном масштабе. В качестве такого параметра

Рис. 7. Гравитационная модель EGM96 (Lemoine et al., 1998)

предложено использовать данные о скоростях движений на поверхности земной коры (рис. 8).

Рис. 8. Карта скоростей горизонтальных движений на поверхности земной коры, мм/год

Представленная на рис. 8 карта создана в Калифорнийском технологическом институте с использованием данных группировки из 30 спутников, входящих в глобальную систему позиционирования .

Данные о скоростях горизонтальных и вертикальных движений на поверхности земной коры обработаны с целью получения распределения значений скоростей этих движений по равномерной сетке как в долготном, так и в широтном направлениях. Процедура обработки выполнялась на основании метода Крайгинга [3; 11; 31]. В результате построены поля распределения векторов скоростей горизонтальных (рис. 9) и вертикальных (рис. 10) движений на поверхности земной коры.

Рис. 9. Распределение поля скоростей горизонтальных движений на поверхности земной коры

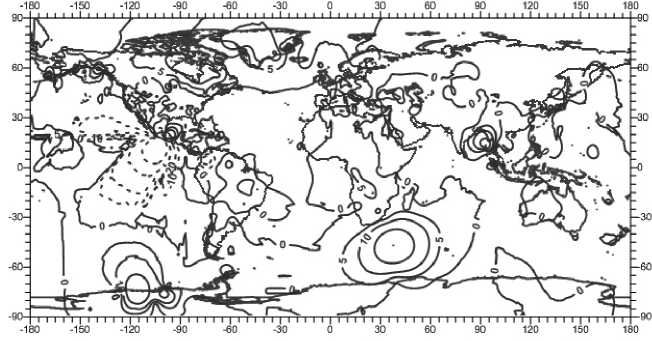
Рис. 10. Распределение поля скоростей вертикальных движений на поверхности земной коры, мм/год. Здесь a z ( x , y , 0) - вертикальная компонента нормальных напряжений на границе литосфера - литосферная мантия; u_z ( x , y , h ) - вертикальная составляющая вектора смещений на поверхности земной коры; u x ( x , y , h ) - x -компонента горизонтальной составляющей вектора смещений на поверхности земной коры; u y ( x , y , h ) - y -компонента горизонтальной составляющей вектора смещений на поверхности земной коры; т _xz ( x , y , h ) - компонента сдвиговых напряжений в плоскости XZ на поверхности земной коры; т yz ( x , y , h ) - компонента сдвиговых напряжений в плоскости YZ на поверхности земной коры; А д и ( x , y ) - величина аномалии гравитационного поля в изостатической редукции в точке с координатами ( x , y ); h ( x , y ) - толщина литосферы в точке с координатами ( x , y ) (в аргументах функций в (9.1) и (9.2) для упрощения толщина литосферы обозначается как h без указания ее аргументов); х - безразмерный коэффициент, равный 10⁶;

t - временной интервал (1 год); рh(x, y) - плотность геологической среды в точке h (x, У)

с координатами ( x , y ), вычисляемая из соотношения р h ( x, y ) = J р ( x, У , z ) dz

Рассмотрим математическую модель напряженно-деформированного состояния литосферы Земли, построенную на основании данных об аномальном гравитационном поле в изостатической редукции и распределении скоростей горизонтальных движений на поверхности земной коры. Величины гравитационных аномалий измеряются в миллигалах (мГал), скорости движений пересчитаны в м/год.

Модель представляется двумя системами уравнений [10]:

'о z ( x , y ,0) = р h ( x , y )A g „ ( x , y)ih ( x , y ),

	u z ( x , y , h ) = v z ( x , y , h ) t ,                                             (91) U x ( x , y , h ) = V x ( x , y , h ) t , _ t xz ( x , y , h ) = 0; ст z ( x , y ,0) = р h ( x , y) A gM ( x , y )x h ( x , y ), U z ( x , y , h ) = V z ( x , y , h ) t ,
	(9.2) U y ( x , y , h ) = V y ( x , y , h ) t , _T yz ( x , y , h ) = 0 .

Для расчета компонент тензора напряжений и составляющих вектора смещений в литосфере достаточно воспользоваться одним из соотношений (9), поскольку выражения для компонент сдвиговых напряжений и компонент горизонтальной составляющей вектора смещений формально одинаковы, различаясь только координатами X и у .

Будем строить выражения для компонент тензора напряжений и составляющих вектора смещений, основываясь на системе уравнений (9.1) и следующих соотношениях (для к -й гармоники), принятых в научной литературе, посвященной оценке гео-динамического риска [1; 19-22; 27; 28]:

ст _z ( x , y , z ) = k ²

—^ C - k ( B + Dz ) X + p

sh kz +

—— D - k ( A + Cz ) X + p

ch kz > cos k x x cos k y y ,

k uz(x, y,z) = T~ I .

2p [^Х + p

2p

D - k ( A + Cz ) sh kz +

^P C - k ( B + Dz ch kz >cos kx cos k y , xy

X + p              JI

k ux (x, y, z) = p- {[ k (B + Dz) + C ] sh kz + [ k (A + Cz) + D ] ch kz} sin kx cos k^y,

т xz ( x , y , z ) = kk x

k ( A + Cz ) + —— D

X + p

sh kz +

k ( B + Dz ) + —— C

X + p

ch kz > sin k_x x cos k_y y ,

где A , B , C , D - неизвестные коэффициенты, определяемые из условий математической модели (9.1).

Подставляя уравнения (10) в соответствующие соотношения системы (9.1) и выполнив необходимые преобразования, приходим к следующей системе уравнений:

k ²1 . ^{p D - kA} | = P h ^{( x} , У ) ^A g „ ^{( x}, У )x ^{h ( x}, У ),

(X + p J

—' ^^ D - k ( A + Ch) 2p[Lx + p

sh kh +

-^ C - k ( B + Dh ) X + p

ch kh ^ = v z (x , y , h ) t ,

-k x - { [ k ( B + Dh ) + C ] sh kh + [ k ( A + Ch ) + D ] ch kh } = v_x ( x , y , h ) t , 2p

k ( A + Ch ) + —— D X + p

sh kh +

k ( B + Dh ) + —— C X + p

ch kh = 0.

Выражая из первого уравнения системы (11) неизвестный коэффициент A , получим:

A = ц D _ P h ⁽ x , y ) A g _и ⁽ x , y ) % ^{h (} x , y )

k ( X + ц )                  k³             ’

2^- D _ kA _ Ckh sh k* + C _ kB _ Dkh X + ц                  X + ц

chM = ^{2 ц} v- ⁽ x,y, ^h ) t k

(kB + Dkh + C) shk* + (kA + Ckh + D) chk* = 2цvx(x, y, h)t, kx kA + Ckh + —— D | shk* +1 kB + Dkh + —— C | chk* = 0.

X + ц J (           X + ц J

Подставляя выражение для коэффициента A в остальные уравнения системы (12) и вводя для удобства расчетов обозначение P g ( x , y ) = р h ( x , y ) A g_u ( x , y ) % h ( x , y ) , придем к следующей системе уравнений:

—^D + P g ⁽ x, y ) _ Ckh ) shkh + ^f      C _ kB _ Dkh ) ch kh = ^{2 ц} v^{z (} x ^, y ^, h ) t ,

X + ц        k²         J IX + ц             J              k

( kB + Dkh + C )sh kh + D I —^ I X + ц

—

P g ^{( x} , y ) k²

+ Ckh ch kh = ^{2 ц} v x ⁽ x , y , h ) t

kx

, (13)

P_ (x, y)

C I ch kh = 0.

D —g-^Д- + Ckh shkh + kB + Dkh +--- k2         J I

Выразим из третьего уравнения системы (13) коэффициент B :

P, ( x, У )

B = g X   th(kh) -[kh + th(kh)]D- -----+ khth(kh) C.(14)

k3                        VX + цJ

Подставив выражение для коэффициента B в первое и второе уравнения системы (13) и выполнив необходимые преобразования, придем к системе, состоящей из двух уравнений:

C + D th( kh )

2 ц ( X + ц ) v z ( x, y, h ) k ( X + 2 ц )

^+^ ch(kh) _ th(kh)sh(kh) ID +1 khch(kh) + — sh(kh) _ khth(kh)sh(kh) IC =

X + ц                   J (         X + ц

= ^{2 ц} v x ⁽ x , y , h ) + P g ( x y ) [ ch( kh ) _ th( kh )sh( kh ) ] .

Получим теперь из первого уравнения системы (15) соотношение для коэффициента C :

C =

2 ц ( X + ц ) v z ( x, y, h ) k ( X + 2 ц )

_ D th( kh ).

С учетом соотношения (16) второе уравнение системы (15) будет содержать только один неизвестный коэффициент D . Приведем окончательное выражение для его нахождения:

D = | 2ц v x ⁽ x , y , h )

I      k x

Pg (xx’ y) [ ch( kh) - th( kh )sh( kh)] - 2^(^+^)vZ^h) x xl kh ch( kh) +

—^Ц— sh( kh ) - kh th( kh )sh( kh )        + 2ц

[ ch( kh ) - th( kh )sh( kh ) ] +

X + ц                      JJ/ [ X + ц

,, ,      Гsh(kh)            )

+ kh sh( kh ) -------th( kh ) -1 >

( ch( kh )          J J

Таким образом, используя соотношения (14), (16), (17) и первое уравнение из системы (12), можно рассчитать компоненты о _z ( x, y, z ) , т xz ( x, y, z ) тензора напряжений и составляющие u_z ( x, y, z ) и u_x ( x, y, z ) вектора смещений в литосфере, представленные в системе (10).

Далее были использованы выражения для u y ( x, y, z ) - составляющей вектора смещений и остальных компонент тензора напряжений [1; 19–22; 27; 28]. Используя эти выражения и систему (10), можно восстановить во всем объеме литосферы поля напряжений (рис. 11) и смещений (рис. 12), соответствующие упругой модели, учитывающей пространственные вариации упругих модулей, поскольку величины λ и μ входят в выражения для компонент тензора напряжений и составляющих вектора смещений.

С учетом величин составляющих полного вектора смещений в геологической среде рассчитаны сдвиговые деформации у _xz, у _yz, у _xy в плоскостях XZ , YZ , XY соответственно из соотношений [6]

Пxz = 1 тxz , Yyz = 1 тyz , Yxy = 1 тxy , (18) [ ц ц ц и затем уже можно построить поле скоростей этих деформаций.

Перейдем к выбору геодинамического индикатора при поиске нефтегазоносных бассейнов.

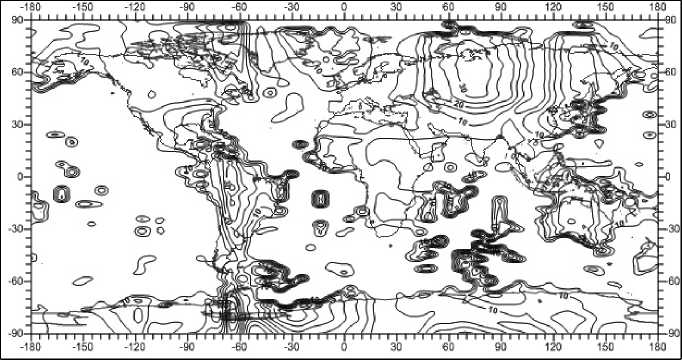
Рис. 11. Распределение сдвиговых напряжений на глубине 3 км, МПа

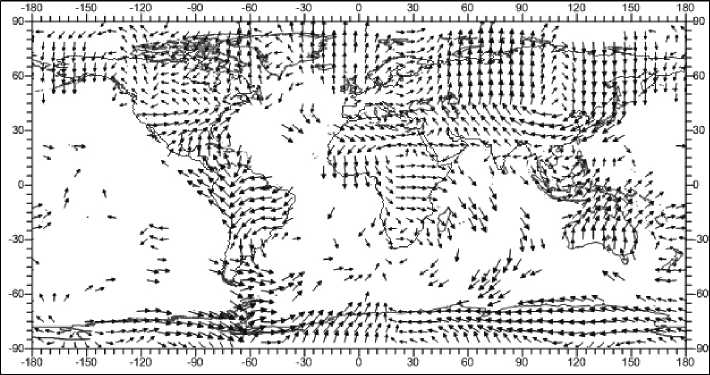
Рис. 12. Распределение горизонтальных смещений на глубине 3 км, усл. ед.

Итак, мы располагаем пятью характеристиками, позволяющими количественно оценивать интенсивность геодинамических процессов: 1) нормальные геодинамиче-ские напряжения; 2) сдвиговые геодинамические напряжения; 3) вертикальные смещения в геологической среде; 4) горизонтальные смещения в геологической среде; 5) скорости сдвиговых деформаций.

Первая из них - нормальные геодинамические напряжения - количественно характеризует способность отдельных слоев и блоков земной коры к сжатию и растяжению под действием приложенных к ним сил, возникающих вследствие влияния гравитационного поля, наличия в литосфере как коровых, так и подкоровых аномалий, а также протекания в ней процессов метаморфоза, об интенсивности которых можно судить по величине поверхностного теплового потока (рис. 13).

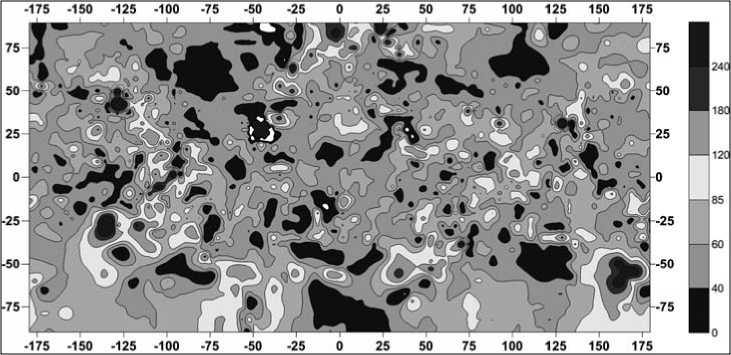
Рис. 13. Распределение поверхностного теплового потока, МВт/м²

Посмотрим, как соотносятся между собой распределение известных нефтегазовых месторождений и особенности распределений вертикальных нормальных напряжений (рис. 14) и горизонтальных нормальных напряжений (рис. 15).

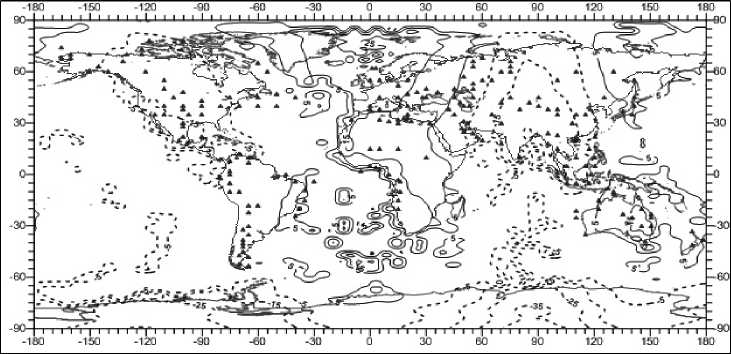
Рис. 14. Распределение нефтегазоносных месторождений и вертикальной компоненты нормальных напряжений, МПа. Глубина 3 км

Видимых закономерностей между распределением нефтегазовых месторождений и особенностями распределения нормальных напряжений, как видно из рис. 14 и 16, не наблюдается. Это позволяет заключить, что первая характеристика не является приоритетной для использования в качестве возможного геодинамического индикатора поиска нефтегазоносных бассейнов.

Теперь рассмотрим вторую характеристику – сдвиговые геодинамические напряжения. Этот показатель, связанный со сдвигом, может иметь определенные шансы на роль такого индикатора, имеющего связь с кольцевыми геологическими структурами [19; 27; 28], являющимися, как полагают [4; 7; 9; 18; 24; 29], своеобразными геоло-

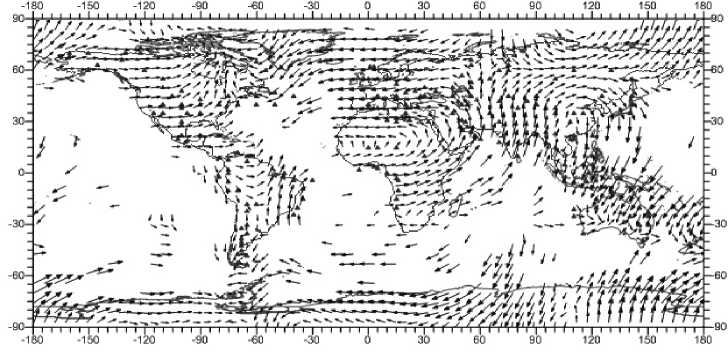
Рис. 15. Распределение нефтегазоносных месторождений и горизонтальных нормальных напряжений, усл. ед. Глубина 3 км гическими «ловушками» применительно к нефтегазовым месторождениям. Однако и эта характеристика также в целом непригодна в качестве геодинамического индикатора для поиска нефтегазовых месторождений, так как и в этом случае четкого соответствия между особенностями распределения сдвиговых напряжений и распределением месторождений не выявлено (рис. 16).

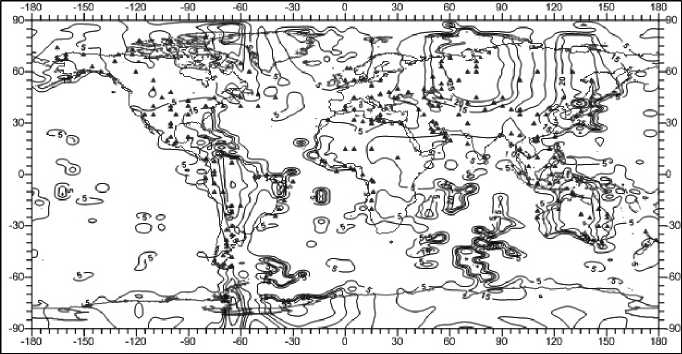
Рис. 16. Распределение нефтегазоносных месторождений и сдвиговых напряжений, МПа. Глубина 3 км

Исследуем третью и четвертую характеристику – вертикальные и горизонтальные смещения в геологической среде. Смещения связаны со сдвигом и могут быть, особенно горизонтальные смещения, интересны на предмет возможности их использования в качестве искомого индикатора.

Посмотрим карты распределений этих характеристик (рис. 17, 19). Особенности распределения вертикальных смещений в литосфере практически не связаны с распределением нефтегазовых месторождений (рис. 17), а вот в распределении векто-

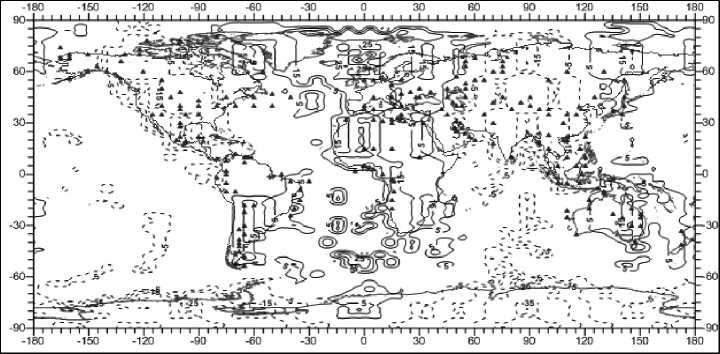
Рис. 17. Распределение нефтегазоносных месторождений и вертикальных смещений в литосфере, мм. Глубина 3 км

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

ров горизонтальных смещений прослеживаются некоторые закономерности. Так, из рис. 18 следует, что некоторые из нефтегазоносных бассейнов соответствуют областям с циркуляциями векторов горизонтальных смещений. Это, в частности, характерно для территорий Северной Америки, Средиземноморья, Центральной Азии и Юго-Восточной Азии.

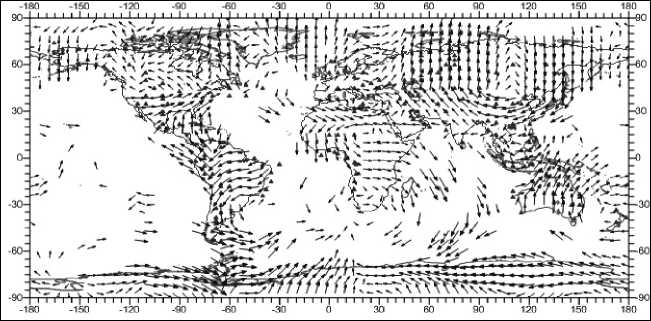
Рис. 18. Распределение нефтегазоносных месторождений и векторов горизонтальных смещений в литосфере, мм. Глубина 3 км

Но еще более устойчивое соответствие можно наблюдать для векторов скоростей горизонтальных сдвиговых деформаций – пятой из рассматриваемых нами характеристик (рис. 19). Соответствующие основные зоны показаны овальными областями. Таким образом, по итогам наших исследований в качестве возможного геодинамиче-ского индикатора поиска нефтегазоносных бассейнов можно предположить распределение векторов скоростей горизонтальных сдвиговых деформаций (РВС ГСД).

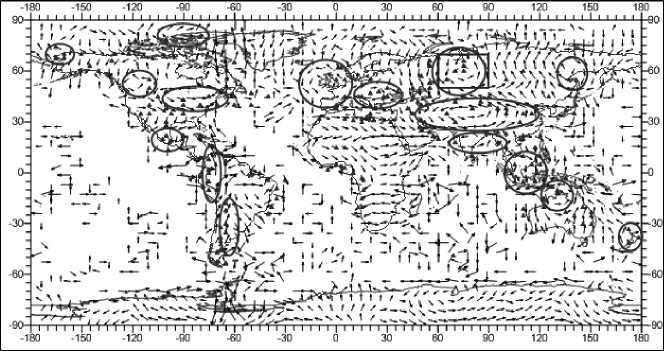
Рис. 19. Распределение нефтегазоносных месторождений и особенности распределения векторов скоростей горизонтальных сдвиговых деформаций, усл. ед.

Эллипсами обозначены области очевидной циркуляции векторов скоростей горизонтальных сдвиговых деформаций. Глубина 3 км. Прямоугольником обозначен Западно-Сибирский нефтегазоносный бассейн

Отметим, что разработанное авторами программно-математическое обеспечение позволяет проводить не только глобальное исследование РВС ГСД, но и локальное, соответствующее имеющимся районам нефтедобычи (рис. 20).

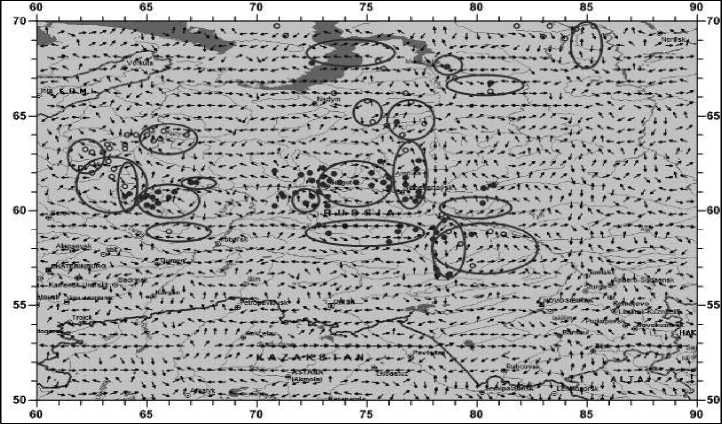
Рис. 20. Распределение нефтяных (круги) и газовых (овалы) месторождений и особенности распределения векторов скоростей горизонтальных сдвиговых деформаций (усл. ед.) для территории Западно-Сибирского нефтегазоносного бассейна. Эллипсами обозначены области очевидной циркуляции векторов скоростей горизонтальных сдвиговых деформаций. Глубина 3 км. Примечательно, что на схеме также прослеживаются вложенные «вихревые» структуры

Выскажем предположение, почему именно эта характеристика – скорость горизонтальных сдвиговых деформаций, наиболее подходит для целей поиска нефтегазовых месторождений.

Как следует из ряда научных источников, анализа материалов изыскательских работ и разведочного бурения в районе известных нефтегазовых месторождений, наряду с нефтегазовыми залежами структурного или тектонического типа, представляющими собой единую залежь с общим контуром нефтеводяного контакта, значительные скопления нефти и газа фиксируются в специфических участках, так называемых локальных геодинамических зонах, расположение которых, как правило, привязано к границам блоков фундамента и региональным разломам [4; 7; 9; 17; 18; 24; 29].

В пределах локальных геодинамических зон под влиянием избыточного давления изменяются физико-механические свойства горных пород и за счет вторичной пористости и трещиноватости возникают участки с повышенными фильтрационными и емкостными свойствами, образующие своеобразные «ловушки» геодинамическо-го типа для углеводородного флюида, мигрирующего по трещинам и разломам и образующего при определенной количественной концентрации нефтегазовую залежь [4; 7; 9; 17; 18; 24; 29].

Изменения скорости сдвиговых деформаций как по величине, так и по направлению (циркуляции векторов скоростей деформаций) указывают на имеющиеся неоднородности в земной коре, обладающие перечисленными выше свойствами. Значительным положительным моментом описанного нами подхода является то, что вычисление полей скоростей сдвиговых деформаций выполняется исключительно

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

методами математического моделирования, когда затраты на проведение подобных исследований минимальны, а эффект достижения требуемого результата может оказаться весьма большим.

Заключение

Активный поиск нефтяных и газовых месторождений продолжается. Используемые на сегодняшний день методы поиска таких бассейнов существенным образом зависят от достоверности информации о геологии исследуемого региона, физико-механических свойствах пород его верхних слоев, особенностях распределения различных геофизических полей и многих других факторов.

В настоящей статье представляется не новый метод, а принципиально новый гео-динамический индикатор (в определенном смысле – даже индикаторное поле), позволяющий по косвенным, математически вычисляемым признакам идентифицировать тот или иной район земного шара как нефтегазоносный. Этот индикатор предлагается искать среди характеристик, определяющих особенности современных движений верхних слоев земной коры.

Для этой цели в работе предложена и обоснована в рамках реологии Ньютона новая математическая модель оценки геодинамических напряжений, смещений и деформаций в литосфере, учитывающей совместное использование информации об аномальном гравитационном поле в изостатической редукции и данных о скоростях движений на поверхности земной коры, а также представлены результаты расчетов, выполненных по этой модели.

По итогам исследований предложен возможный геодинамический индикатор поиска нефтегазоносных бассейнов – распределение скоростей сдвиговых деформаций, и высказано предположительное обоснование целесообразности его использования.

Разумеется, материал представленной статьи и сам предложенный геодинамиче-ский индикатор не следует использовать в качестве конечного инструментария для поиска нефтегазовых месторождений на локальных участках. Подход, описанный в работе, имеет отношение к масштабным нефтегазоносным бассейнам и может применяться в рамках глобальной математической модели оценки напряжений, смещений и деформаций. Однако имеющиеся к настоящему моменту информационно-технические возможности позволяют на основании развития математических моделей и соответствующих численных методов создать и практически реализовать точную и эффективную методику поиска нефтегазовых месторождений на локальных участках континентальных и шельфовых территорий.

• 1.    Абрамова А.В., Бондарь К.М., Данилов Р.М., Минаев В.А., Павлова С.А., Попов А.Н., Фаддеев А.О. Моделирование геодинамических рисков в чрезвычайных ситуациях : монография / под ред. К.М. Бондаря, В.А. Минаева, А.О. Фаддеева. – Хабаровск : Изд-во Дальневост. юрид. ин-та МВД России, 2014. – 124 с.

• 2.    Антонова Е.О. Основы нефтегазового дела. – М. : Недра – Бизнес центр, 2003. – 307 с.

• 3.    Аронов В.И. Методы построения карт геолого-геофизических признаков и геометризация залежей нефти и газа на ЭВМ. – М. : Недра, 1990. – 301 с.

• 4 .    Басарыгин Ю.М., Булатов А.И., Проселков Ю.М. Бурение нефтяных и газовых скважин. – М. : Недра – Бизнес центр, 2002. – 632 c.

• 5.    Басарыгин М.Ю., Басарыгин Ю.М., Булатов А.И. Строительство и эксплуатация морских нефтяных и газовых скважин : в 4 т. / отв. ред. А.И. Булатов. – Краснодар : Просвещение – Юг, 2003. – Т. 4. – Кн. 3. – 342 с.

• 6.    Биргер И.А., Мавлютов Р.Р. Сопротивление материалов : учеб. пособие. – М. : Наука, 1986. – 560 с.

• 7.    Вадецкий Ю.В. Бурение нефтяных и газовых скважин. – М. : Изд. центр «Академия», 2013. – 352 c.

• 8.    Викулин А.В . Физика Земли и геодинамика. – Петропавловск-Камчатский : КамГУ им. Витуса Беринга, 2008. – 463 с.

• 9.    Гиматудинов Ш.К. Физика нефтяного и газового пласта : учебник. – 2-е изд., перераб. и доп. – М. : Недра, 2005. – 312 с.

• 10.    Грачев Д.С., Минаев В.А., Топольский Н.Г., Фаддеев А.О. Методы оценки температурного поля литосферы Земли как источника геодинамических угроз для зон шельфовой нефтегазодобычи // Технологии техносферной безопасности : Интернет-журн. – Вып. 5 (75). – 2017 [Электронный ресурс]. – Режим доступа: http://agps-2006 . narod.ru/ttb/2017-5/21-04-17.ttb.pdf/ (дата обращения: 30.11.2017).

• 11.    Давид М. Геостатистические методы при оценке запасов руд. – Л. : Недра, 1980. – 360 с.

• 12.    Коршак А.А. Основы нефтегазового дела. – Уфа : Изд-во ДизайнПолиграф-Сервис, 2005. – 528 с.

• 13.    Кременецкий М.И., Ипатов А.И., Гуляев Д.Н. Информационное обеспечение и технологии гидродинамического моделирования нефтяных и газовых залежей. – М. : Ин-т компьютер. исслед., 2012. – 894 c.

• 14.    Кузьмин Ю.О., Жуков В.С. Современная геодинамика и вариации физических свойств горных пород. – М. : Горная кн., 2012. – 264 с.

• 15.    Лобковский Л.И., Никишин А.М., Хаин В.Е. Современные проблемы геотектоники и геодинамики. – М. : Науч. мир, 2004. – 612 с.

• 16.    Лысенко В.Д. Разработка нефтяных месторождений. Проектирование и анализ. – М. : Недра – Бизнес центр, 2003. – 638 c.

• 17.    Лысенко В.Д., Грайфер В.И. Разработка малопродуктивных нефтяных месторождений. Development of Low-Productive Oil Deposits. На русском и английском языках. – М. : Недра, 2001. – 565 c.

• 18.    Милосердова Л.В. Геология, поиски и разведка месторождений нефти и газа : конспект лекций / под ред. к.г.-м.н., доц. В.Г. Мартынова. – М., 2003. – 179 с.

• 19.    Минаев В.А., Фаддеев А.О . Оценки геоэкологических рисков. Моделирование безопасности туристско-рекреационных территорий. – М. : Финансы и статистика; Изд. дом ИНФРА-М, 2009. – 370 с.

• 20.    Минаев В.А., Фаддеев А.О., Бондарь К.М., Сычев М.П., Видов С.В., Кираков-ский В.В., Кузьменко Н.А., Попов А.Н. Математическое моделирование геодинамиче-ских рисков: оценки и перспективы / под ред. В.А. Минаева, А.О. Фаддеева, К.М. Бондаря. – Хабаровск : Изд-во Дальневост. юрид. ин-та МВД России, 2015. – 212 с.

• 21.    Минаев В.А., Фаддеев А.О., Кузьменко Н.А. Моделирование и оценка геодина-мических рисков. – М. : РТСофт – Космоскоп, 2017. – 256 с.

• 22.    Минаев В.А., Топольский Н.Г., Фаддеев А.О., Бондарь К.М., Мокшанцев А.В. Геодинамические риски и строительство. Математические модели. – М. : Акад. ГПС МЧС России, 2017. – 208 с.

• 23.    Покрепин Б.В. Эксплуатация нефтяных и газовых скважин. – М. : ИнФолио, 2011. – 496 c.

• 24.    Сваровская Н.А. Физика пласта : учеб. пособие. – Томск : Изд-во ТПУ, 2003. – 155 с.

• 25.    Тагиров К.М. Эксплуатация нефтяных и газовых скважин. – М. : Изд. центр «Академия», 2012. – 336 c.

• 26.    Теркот Д., Шуберт Дж. Геодинамика : в 2 т. – М. : Мир, 1985. – 730 с.

• 27.    Фаддеев А.О. Геоэкологический аспект функционирования подразделений УИС и управления ими. – Рязань : Акад. права и упр. Минюста России, 2003. – 190 с.

• 28.    Фаддеев А.О., Данилов Р.М. Геодинамическая безопасность ландшафтно-территориальных комплексов / под ред. В.А. Минаева. – Хабаровск : Изд-во Дальневост. юрид. ин-та МВД России, 2010. – 132 с.

• 29.    Фазлыев Р.Т. Площадное заводнение нефтяных месторождений. – М. ; Ижевск : ИКИ РАН, НИЦ «Регулярная и хаотическая динамика», 2008. – 256 с.

• 30.    Хаин В.Е., Ломизе М.Г. Геотектоника с основами геодинамики. – М. : Моск. у-т, 2005. – 560 с.

• 31.    Kerry, K.E., Hawick, K.A. Kriging Interpolation on High-Performance Computers [Электрон. ресурс]. Department of Computer Science, University of Adelaide, SA 5005, Australia. Technical Report DHPC-035. – Режим доступа: http://acsys.adelaide.edu.au/re-ports//035/abs-035.html

  • 1.    Abramova, A.V., Bondar, K.M., Danilov, R.M., Minaev, V.A., Pavlova, S.A., Popov, A.N., Faddeev, A.O. Modelirovanie geodinamicheskikh riskov v chrezvychaynykh situatsiyakh : monografiya / pod red. K.M. Bondarya, V.A. Minaeva, A.O. Faddeeva. – Khabarovsk : Dalnevost. yurid. in-t MVD Rossii, 2014. – 124 s.

  • 2.    Antonova, E.O. Osnovy neftegazovogo dela. – M. : Nedra – Biznes tsentr, 2003. – 307 s.

  • 3.    Aronov, V.I. Metody postroeniya kart geologo-geofizicheskikh priznakov i geometrizatsiya zalezhey nefti i gaza na EVM. – M. : Nedra, 1990. – 301 s.

  • 4.    Basarygin, Yu.M., Bulatov, A.I., Proselkov, Yu.M. Burenie neftyanykh i gazovykh skvazhin. – M. : Nedra – Biznes tsentr, 2002. – 632 s.

  • 5.    Basarygin, M.Yu., Basarygin, Yu.M., Bulatov, A.I . Stroitel’stvo i ekspluatatsiya morskikh neftyanykh i gazovykh skvazhin : v 4 t. / otv. red. A.I. Bulatov. – Krasnodar : Prosveshchenie – Yug, 2003. – T. 4. – Kn. 3. – 342 s.

  • 6.    Birger, I.A., Mavlyutov, R.R. Soprotivlenie materialov : uchebnoe posobie. – M. : Nauka, 1986. – 560 s.

  • 7.    Vadetskiy, Yu.V. Burenie neftyanykh i gazovykh skvazhin. – M. : Izd. tsentr “Akademiya”, 2013. – 352 c.

  • 8.    Vikulin, A.V. Fizika Zemli i geodinamika. – Petropavlovsk-Kamchatskiy : KamGU im. Vitusa Beringa, 2008. – 463 s.

  • 9.    Gimatudinov, Sh.K. Fizika neftyanogo i gazovogo plasta : uchebnik. – 2-e izd., pererab. i dop. – M. : Nedra, 2005. – 312 s.

  • 10.    Grachev, D.S., Minaev, V.A., Topol’skiy, N.G., Faddeev, A.O . Metody otsenki temperaturnogo polya litosfery Zemli kak istochnika geodinamicheskikh ugroz dlya zon shel’fovoy neftegazodobychi // Tekhnologii tekhnosfernoy bezopasnosti: Internet-zhurn. – Vyp. 5 (75). – 2017 [Elektronnyy resurs]. – Rezhim dostupa: http://agps-2006.narod.ru/ ttb/2017-5/21-04-17.ttb.pdf/ (data obrashcheniya: 30.11.2017).

  • 11.    David, M. Geostatisticheskie metody pri otsenke zapasov rud. – L. : Nedra, 1980. – 360 s.

  • 12.    Korshak, A.A. Osnovy neftegazovogo dela. – Ufa : Izd-vo DizaynPoligrafServis, 2005. – 528 s.

  • 13.    Kremenetskiy, M.I., Ipatov, A.I., Gulyaev, D.N. Informatsionnoe obespechenie i tekhnologii gidrodinamicheskogo modelirovaniya neftyanykh i gazovykh zalezhey. – M. : In-t komp’yuter. issled., 2012. – 894 s.

  • 14.    Kuz’min, Yu.O., Zhukov, V.S. Sovremennaya geodinamika i variatsii fizicheskikh svoystv gornykh porod. – M. : Gornaya kniga, 2012. – 264 s.

  • 15.    Lobkovskiy, L.I., Nikishin, A.M., Khain, V.E. Sovremennye problemy geotektoniki i geodinamiki. – M. : Nauch. mir, 2004. – 612 s.

  • 16.    Lysenko, V.D. Razrabotka neftyanykh mestorozhdeniy. Proektirovanie i analiz. – M. : Nedra – Biznes tsentr, 2003. – 638 s.

  • 17.    Lysenko, V.D., Grayfer, V.I. Razrabotka maloproduktivnykh neftyanykh mesto-rozhdeniy. Development of Low-Productive Oil Deposits. Na russkom i angliyskom yazykakh. – M. : Nedra, 2001. – 565 s.

  • 18.    Miloserdova, L.V. Geologiya, poiski i razvedka mestorozhdeniy nefti i gaza : konspekt lektsiy / pod red. k.g.-m.n., dots. V.G. Martynova. – M., 2003. – 179 s.

  • 19.    Minaev, V.A., Faddeev, A.O . Otsenki geoekologicheskikh riskov. Modelirovanie bezopasnosti turistsko-rekreatsionnykh territoriy. – M. : Finansy i statistika; Izd. dom INFRA-M, 2009. – 370 s.

  • 20.    Minaev, V.A., Faddeev, A.O., Bondar’, K.M., Sychev, M.P., Vidov, S.V., Kirakov-skiy, V.V., Kuz’menko, N.A., Popov, A.N .Matematicheskoemodelirovaniegeodinamicheskikh riskov: otsenki i perspektivy / pod red. V.A. Minaeva, A.O. Faddeeva, K.M. Bondarya. – Khabarovsk : Izd-vo Dal’nevost. yurid. in-ta MVD Rossii, 2015. – 212 s.

  • 21.    Minaev, V.A., Faddeev, A.O., Kuz’menko, N.A . Modelirovanie i otsenka geodinami-cheskikh riskov. – M. : RTSoft – Kosmoskop, 2017. – 256 s.

  • 22.    Minaev, V.A., Topol’skiy, N.G., Faddeev, A.O., Bondar’, K.M., Mokshantsev, A.V. Geodinamicheskie riski i stroitel’stvo. Matematicheskie modeli. – M. : Akad. GPS MCHS Rossii, 2017. – 208 s.

  • 23.    Pokrepin, B.V. Ekspluatatsiya neftyanykh i gazovykh skvazhin. – M. : InFolio, 2011. – 496 s.

  • 24.    Svarovskaya, N.A. Fizika plasta : uchebnoe posobie. – Tomsk : Izd-vo TPU, 2003. – 155 s.

  • 25.    Tagirov, K.M . Ekspluatatsiya neftyanykh i gazovykh skvazhin. – M. : Izd. tsentr “Akademiya”, 2012. – 336 s.

  • 26.    Terkot, D., Shubert, Dzh . Geodinamika : v 2 t. – M. : Mir, 1985. – 730 s.

  • 27.    Faddeev, A.O. Geoekologicheskiy aspekt funktsionirovaniya podraz-deleniy UIS i upravleniya imi. – Ryazan’ : Akad. prava i upr. Minyusta Rossii, 2003. – 190 s.

  • 28.    Faddeev, A.O., Danilov, R.M . Geodinamicheskaya bezopasnost’ land-shaftno-terri-torial’nykh kompleksov / pod red. V.A. Minaeva. – Khabarovsk : Izd-vo Dal’nevost. yurid. in-ta MVD Rossii, 2010. – 132 s.

  • 29.    Fazlyev, R.T. Ploshchadnoe zavodnenie neftyanykh mestorozhdeniy. – M. ; Izhevsk : IKI RAN, NITS “Regulyarnaya i khaoticheskaya dinamika”, 2008. – 256 s.

  • 30.    Khain, V.E., Lomize, M.G. Geotektonika s osnovami geodinamiki. – M. : Mosk. un-t, 2005. – 560 s.

  • 31.    Kerry, K.E., Hawick, K.A. Kriging Interpolation on High-Performance Computers [Elektron. resurs]. Department of Computer Science, University of Adelaide, SA 5005, Australia. Technical Report DHPC-035. – Rezhim dostupa: http://acsys.adelaide.edu.au/ reports//035/abs-035.html

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»