Геометрическая интерпретация аналитических категорий как основа осознанного освоения математического содержания

Проблема формирования понятий у учащихся не теряет своей актуальности как в XX в., так и в настоящее время. В условиях становления информационного общества изменяются требования к средствам и методам формирования математических понятий на уроках и во внеурочной работе. Широко используемые в XX в. средства и методы, опирающиеся на синтез и обобщения, перестают быть эффективными при работе с обучающимися, у которых преобладает «кликовое» мышление, которые с детства привыкли к динамическим объектам, анимационным эффектам и т. п.

На уроках математики особое место занимает работа с математическими понятиями как «результатом выделения из предметов и явлений окружающего мира количественных и пространственных свойств и отношений и абстрагирования их от всех других свойств» [2]. В тоже время в современных учебниках разделяют понятия и аналитические категории. Последние – это такие понятия, которые являются только родами по отношению к другим понятиям, не могут быть видами в отношении «род – вид». У категорий наибольший объем и наименьшее содержание по сравнению с остальными понятиями.

Учитывая вышесказанное и тенденции развития математического образования в России, мы приходим к необходимости использования геометрических интерпретаций при формировании у учащихся математических понятий и аналитических категорий. Геометрическая интерпретация – это объяснение математического процесса или связи между объектами с помощью геометрических методов или иллюстраций. Мы исходим из того, что любую статичную иллюстрацию, демонстрирующую геометрическую интерпретацию, можно сделать анимированной или динамичной. В рамках данной статьи приведены примеры статичных иллюстраций, которые легко преобразуемы в динамичные средствами “Power Point”, “Macromedia Flash” или создания видеоролика.

Как отмечает Л.С. Выготский, геометрическая интерпретация аналитических категорий и понятий обеспечивает формирование у учащихся более глубокого и осознанного понимания смысла каждой формулы, теоремы, аксиомы и математического предложения, которые «как бы оживают», а также доступное восприятие абстрактной математической информации [1]. В отечественной методике обучения математике исследователи неоднократно обращались к вопросу обучения аналитическим категориям с опорой на геометрические образы, однако акцент делался на использование иллюстраций как средства наглядности при обучении. При этом до настоящего времени не сформировалось целостной методики, обеспечивающей осознанное освоение математического содержания на основе геометрических интерпретаций.

Рассмотрим несколько примеров геометрического истолкования способов возведения в квадрат чисел, оканчивающихся цифрой 5.

Например: 352 = 30 · 40 + 25 = 1225. Геометрическое объяснение: необходимо вычислить площадь квадрата со сторонами в 35 единиц. Перемещая, как указано на рис. 1 заштрихованный прямоугольник, получим «новый» прямоугольник со сторонами 35 и 40. Определим площадь этого прямоугольника и, прибавляя к ней площадь квадрата со стороной 5 единиц, получим площадь искомого квадрата (см. рис. 1).

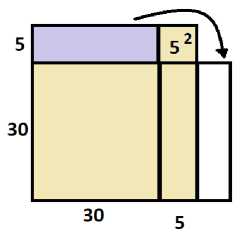
Рис. 1. Вычисление квадрата 35

Аналогичными будут геометрические иллюстрации вычисления значений квадратов следующих чисел:

6,22 = 6 • 7 + 0,5:2 = 42,25 (8-) = 8 • 9 + - = 72- и

Мы исходим из того, что геометрические интерпретации необходимо использовать не только при возведении в квадрат чисел. Геометрическая интерпретация основного свойства бесконечно убывающей геометрической прогрессии: сумма ее членов при безграничном увеличении числа не растет беспредельно, а приближается к определенной предельной величи-

1 , 1 , 1 , 1 , 1 Iт не, которую принимают за сумму этой прогрессии. Например:,

/                            х v n — 1 х                        2    4   816

• i-              /          1      1      11

• т. е.                                               . Данный предел можно на иллюстрации на

глядно представить в виде предела суммы площадей бесконечного числа прямоугольников, уменьшающихся по площади (см. рис. 2).

1	1 2
	1 4		L
		1 16	1/32

Рис. 2. Геометрическая интерпретация основного свойства бесконечно убывающей геометрической прогрессии

Наглядно на рис. 2 на с. 14 показано, что чем больше на рисунке прямоугольников, тем меньше сумма этих площадей будет отличаться от площади двух квадратов. Аналогичной будет иллюстрация суммы ряда                     .

• 2   9   27

Т.К. Смыковская указывает на целесообразность применения геометрических иллюстраций при исследовании алгебраических выражений [3]. Например: a · b – площадь прямоугольника со сторонами а, b; а² – площадь квадрата построенного по стороне а; a³ – это площадь куба, ребро которого равно а .

Такие задания следует включать в математические или графические диктанты.

Прием геометрической иллюстрации широко используется для демонстрации алгебраических тождеств формул площадей и объемов.

С.Е. Ляпин предлагает обобщать формулы сокращенного умножения с геометрической точки зрения (см. рис. 3) [2].

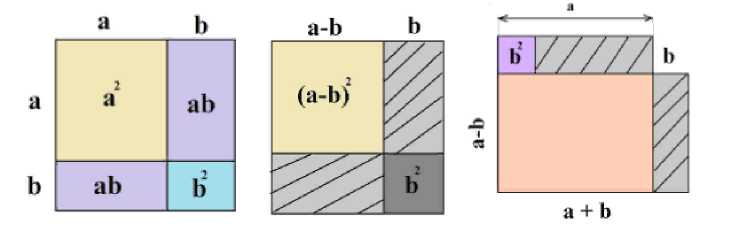
Рис. 3. Геометрическое представление формул сокращенного умножения

Работая с геометрическими интерпретациями, учащиеся формулируют выводы, обобщая материал, показывая связь алгебры с геометрией.

Например:

• 1.    Формула квадрата двучлена показывает, как меняется площадь квадрата при увеличении каждой его стороны на несколько единиц.

• 2.    Формула (a — ЬУ = a² — 2.ab + b² выражает изменение площади квадрата, если каждую его сторону уменьшить на несколько единиц.

• 3.    Формула произведения разности двух выражения их суммы дает ответ на вопрос, как меняется площадь квадрата, если одну его сторону уменьшить на несколько единиц, а другую увеличить на столько же единиц (при неизменном периметре).

В опоре на представленные выше выводы и учитывая графические иллюстрации, учащиеся могут сделать следующие выводы: 1) в первых двух случаях изменение площади зависит, как от стороны первоначального квадрата, так и от увеличения их стороны; 2) в третьем случае изменение площади зависит только от изменения величины стороны, т. е. не зависит от стороны первоначального квадрата.

Геометрические иллюстрации продуктивно используются для геометрического истолкования применения формул произведения суммы и разности двух выражении для устных вычислений.

Например, можно предложить следующие задания, предварительно рассмотрев формулу: a² — b² = (a — bXa + b"). Ее геометрический смысл заключается в следующем: если одну сторону лобового квадрата уменьшить на несколько единиц ( b ), одновременно другую строну увеличить на столько же единиц, то площадь обычного прямоугольника будет меньше площади первоначального квадрата на b² .

Рассмотрим задания для устного счета, предусматривающие опору на геометрическую интерпретацию аналитических категорий, в том числе и формул сокращенного умножения.

Задание 1. Вычислите.

Рассуждения: вычисляется площадь прямоугольника со сторонами 43 и 37 единиц. Вместо этого можно вычислить площадь квадрата со стороной 40 и вычесть площадь квадрата со стороной 3, т. е..

Задание 2. Вычислите.

Рассуждение: если любую строну квадрата уменьшить на одну единицу, а другую увеличить на одну единицу то площадь уменьшается на 12, независимо от стороны первоначального квадрата. .

Задание 3. Не производя вычислений, определите площадь какого земельного участка больше и на сколько – квадрата со стороной 100 м или прямоугольника со сторонами: а) 140м и 60м, б) 95 и 105, в) 101,5 и 98,5.

Рассуждения: делается вывод, что наибольшей будет площадь 100 ∙ 100, т. е. площадь в 1 га, при этом площадь каждого участка сравнивается с площадью в 1 га. Геометрическую иллюстрацию можно анализировать, рассматривая вопрос о периметрах этих участков.

Так же в устную работу на уроках необходимо включать задания, при решении которых требуется, не производя вычислений, устанавливать, что больше и на сколько:

• а) 372или 38-36; б) 372или37-- -

• '                    22

• в) а2или(а— 1,5)(а + 1,5)при a > 1,5; г) 128 • 125 или(126,5)2.

Так же, используя графическую иллюстрацию, можно показать, что целесообразно разность квадратов двух чисел представлять следующим образом:                             .

Например,

;

.

Задание. Вычислите: (19,7)2. Можно провести следующие рассуждения: вычисляется площадь квадрата со стороной 19,7, при этом это действие можно заменить на вычисление площади прямоугольника со сторонами 20 и 19,4, к которой прибавляется площадь квадрата со стороной 0,3. .

Такой прием решения дает возможность возводить некоторые числа в квадрат устно, т. к. один из сомножителей округляется и умножается на однозначное число. Это тождество можно пояснить с опорой на рис. 4. Используются следующие рассуждения: площадь со стороной квадрата со стороной а равна площади прямоугольника со сторонами a - b и a + b , сложенным с площадью квадрата со стороной b .

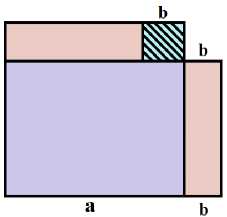
Рис. 4. Вычисление площади квадрата с помощью площадей прямогугольников

Итогом такой работы станет то, что учащиеся смогут сделать обобщение о том, что квадрат обладает замечательным свойством по сравнению с другими прямоугольниками того же периметра: он имеет наибольшую площадь. При равных площадях на всех прямоугольниках он обладает наименьшим периметром, это свойство имеет практическое значение, например, при построении домов. Основание дома по возможности делают квадратное или близкое по возможности к квадратному, в зависимости от строительного материала.

Таким образом, использование геометрической интерпретации позволяет сформировать не только вычислительные навыки и показать практическую направленность обучения математики, но и формировать систему математических понятий и категорий, обеспечивать осознанное освоение математического содержания.