Геометрия фазовых диаграмм четверных водно-солевых систем простого эвтонического типа

Состояния многокомпонентной физико-химической системы описываются правилом фаз Гиббса, принципами соответствия и непрерывности, предложенными Кур-наковым [1].

Фазовые диаграммы используются для их анализа с целью определения составов и соотношений равновесных фаз и решения различных прикладных задач химической технологии. Построение математических моделей позволяет быстро устанавливать природу, состав и соотношения равновесных фаз.

Анализ таких систем осложняется тем, что размерность пространства фазовой диаграммы зависит от количества компонентов водно-солевой системы. Если диаграмма тройной системы, исследованной в изобарноизотермических условиях, может быть изображена на плоскости, то таковая четверная система является трехмерным объектом. Наглядно представление фазовых диаграмм растворимости большей размерности возможно только в виде оптимальных проекций.

В статье рассмотрена геометрическая структура фазовых диаграмм разных размерностей, исследованная в изобарноизотермических условиях, для систем простого эвтонического типа без образования кристаллогидратов и ограниченных рядов твердых растворов. Предложен способ вычисления физико-химических характеристик: плотности и показателя преломления в точках, находящихся на поверхности ликвидуса, составов смесей компонентов на границах и гранях фазовых областей – на основе имеющихся экспериментальных данных. Описано математическое содержание модуля визуализации фазовых диаграмм четверных водносолевых систем рассматриваемого типа.

• 1.    Фазовые диаграммы водно-солевых систем простого эвтоничсекого типа

  • 1.1.    Тройные водно-солевые системы простого эвтонического типа

Тройная водно-солевая система простого эвтнического типа согласно правилу фаз и принципам соответствия и непрерывности состоит из трех компонентов и включает восемь фазовых областей. Фазовая диаграмма ее изображается в виде равностороннего треугольника, образованного вершинами (S1, S2 и H2O). В нем боковые ребра S1–H2O и S2–H2O являются оконтуривающими двойными системами. Точки R1 и R2 соответствуют растворимостям в этих системах при данной температуре, точка E – эвтоника – составу насыщенного при постоянном давлении и темпе- ратуре раствора, находящегося в нонвариант-ном равновесии с двумя или более твердыми фазами [2].

Внутреннее пространство треугольника

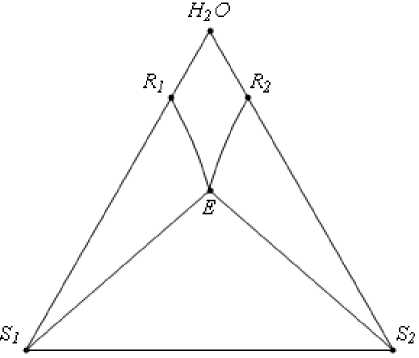
Рис. 1. ФДР тройной водно-солевой системы простого эвтоничсекого типа

(рис. 2) делится на четыре фазовые области:

• 1)    область совместной кристаллизации двух солей (рис. 3, а);

• 2)    две области кристаллизации одной соли (рис. 3, б):

область кристаллизации соли S 1 – область

S1R1E, область кристаллизации соли S2 – область S2R2E;

• 3)    область ненасыщенных растворов (рис. 3, в).

Кривые R₁E и R₂E называются ветвями растворимости и являются линиями монова-риантного равновесия солей S₁ и S₂ и соответствующих насыщенных растворов. В настоящее время не существует аналитического описания этих кривых, поэтому они строятся приближенно по имеющимся экспериментальным данным.

• 1.2.    Четверные водно-солевые системы простого эвтонического типа

Изотерма и изобара четверной системы изображается уже в виде тетраэдра в трехмерном пространстве состояния (рис. 4, а).

Как следует из правила фаз и принципов непрерывности и соответствия, структура диаграммы системы простого эвтонического типа усложнилась и содержит восемь фазовых областей. Можно заметить, что боковые ребра пирамиды являются оконтуривающими двойными системами, боковые грани – окон-туривающими тройными системами, а внутренняя часть ее – собственно четверной системой.

С увеличением числа компонентов системы увеличивается размерность пространства фазовой диаграммы, количество и разнообразие фазовых областей.

Внутреннее пространство тетраэдра делится на восемь фазовых областей:

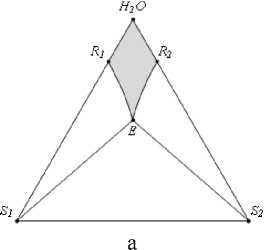
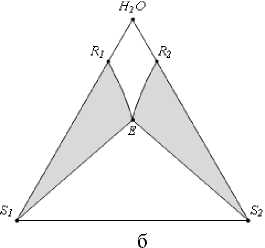
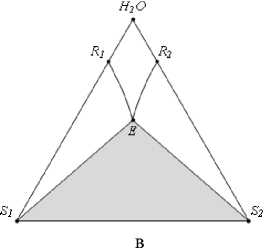
Рис. 3. Фазовые области на ФДР тройной водно-солевой системы простого эвтонического типа

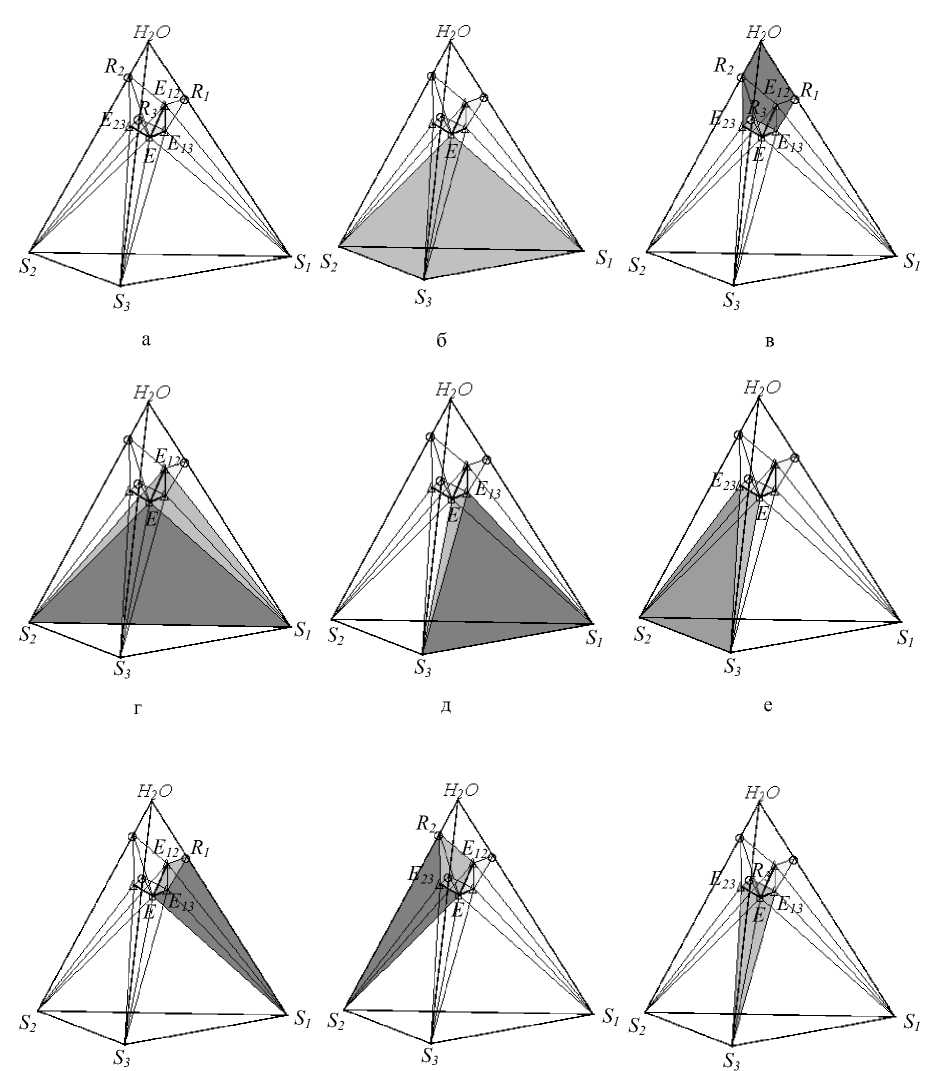
• 1)    область совместной кристаллизации всех трех солей - пирамида S 1 S 2 S 3 E (рис. 4, б);

• 2)    три области кристаллизации двух солей: область совместной кристаллизации солей S 1 и S 2 (рис. 4, г),

область совместной кристаллизации солей S1 и S3 (рис. 4, д), область совместной кристаллизации со- лей S2 и S3 (рис. 4, е);

• 3)    три области кристаллизации одной соли: область кристаллизации соли S 1 (рис.4,ж),

область кристаллизации соли S 2 (рис.4, з), область кристаллизации соли S 3 (рис.4, и);

• 4)    область ненасыщенных растворов - область H 2 O - R 1 E 12 R 2 E 23 R 3 E 13 (рис. 4, в).

  

  и

  ж

  з

  Рис. 4. Фазовые области ФДР четверной водно-солевой системы простого эвтонического типа

  
  

• 2.Структура фазовых диаграмм водно-солевых систем простого эвтонического типа

Линии моновариантного равновесия E 12 E, E 13 E, E 23 E являются кривыми, восстановленными по экспериментальным данным.

Поверхности кристаллизации R 1 E 12 EE 13 , R 2 E 23 EE 12 и R 3 E 13 EE 23 солей S 1 , S 2 и S 3 соответственно также не имеют аналитического описания и на практике строятся по данным экспериментов.

Как видно из приведенного материала, с увеличением числа компонентов водносолевой системы увеличивается размерность пространства фазовой диаграммы, количество и разнообразие фазовых областей внутри самой диаграммы.

Введем обозначения: d - размерность пространства фазовой диаграммы, k - число компонентов водно-солевой системы.

Для построения фазовых диаграмм растворимости простых эвтонических систем применяют метод Гиббса-Розебома [1], использующий барицентрические координаты.

Диаграмма к- компонентной водносолевой системы изображается в виде d-мерного симплекса, каждая вершина которого соответствует компоненту системы, причем d = к -1. (1)

Любая точка внутри симплекса соответствует некоторой смеси компонентов, причем состав этой смеси определяет координаты этой точки. Пусть данной смеси X соответствуют массовые концентрации компонентов системы x 1 , x₂ ,., x k , тогда сумма этих концентраций всегда составляет 100%. Поэтому, зная солевой состав, всегда можно вычислить долю воды:

к - 1

Х к = 100 - £ х^ (2)

i = 1

Таким образом, любой состав системы описывается точкой d -мерного пространства.

Так как компоненты рассматриваемой простой водно-солевой системы эвтоническо-го типа не вступают в химические реакции друг с другом, возможно выпадение солей в осадок в любом сочетании.

Пусть t - количество солей, находящихся в твердой фазе (t=0, 1, ., к-1). Тогда ко- личество различных фазовых областей, содержащих t твердых фаз, равно числу сочетаний:

ф t = с к - 1 .                  (3)

Общее количество фазовых областей на фазовой диаграмме простой к -компонентной системы равно в изобарно-изотермических условиях:

к - 1

Ф = £ ф t = 2 ^{к - 1}.              (4)

t = 0

Описание структуры диаграммы сводится к определению ее фазовых областей. Рассмотрим (2 ^{к - 1} - 1) фазовые области, в которых хотя бы одна соль находится в твердой фазе ( t= 1, 2, ..., к -1). Каждая такая область содержит t точек состава компонентов, отвечающих солям, выпавшим в осадок, и точки, образующие геометрические образы фазовых равновесий различной вариантности.

Размерность этих образов можно определить с помощью правила фаз Гиббса [2], с учетом постоянного давления и температуры в системе:

v + f = к + 0 .           (5)

Здесь f - число фаз, v - число степеней свободы (или вариантность) [2]. Так как число фаз в данном случае равно t+1, число степеней свободы v = к -1 -1.              (6)

Составы фаз, участвующих в нонвари-антном равновесии ( v =0), отображается точками, в моновариантных равновесиях ( v =1) -линиями, в дивариантных равновесиях ( v =2) -поверхностями, в тривариантных и более ( v >3) - гиперповерхностями. Поливариантные равновесия не имеют аналитического описания и строятся приближенно по наборам точек, которые находятся на этих поверхностях.

Важной задачей является определение составов равновесных фаз для любой исходной реакционной смеси данной водно-солевой системы. Для этого необходимо решить задачу определения фазовой области, в которой лежит фигуративная точка, соответствующая составу данной исходной смеси компонентов (ИСК), который может находиться в любой из 2 ^{к - 1} фазовых областей.

Задача по определению местоположения ИСК решается путем последовательного исключения фазовых областей, в которые не попадает данная фигуративная точка.

Оптимальная последовательность проверки областей кристаллизации фазовой диаграммы рассматриваемых четверных водносолевых систем, на наш взгляд, должна быть следующей:

• 1)    четырехфазная область кристаллизации трех солей (рис. 4, б);

• 2)    три трехфазные области кристаллизации двух солей (рис. 4, г, д, е);

• 3)    три двухфазные области кристаллизации одной соли (рис. 4, ж, з, и);

• 4)    область ненасыщенных растворов (рис. 4, в).

• 2.1.    Определение положения фигуративной точки относительно симплекса

На каждом шаге проверки фазовые области кристаллизации t солей ( t=1, 2, .., к -2) разбиваются на совокупность непересекающихся d -мерных симплексов, и определяется положение точки F относительно каждого из них. Если фигуративная точка принадлежит хотя бы одному из симплексов разбиения, то делается вывод о принадлежности этой точки данной фазовой области.

Пусть фигуративная точка F имеет координаты в d -мерном пространстве:

F ( x ( ^F ) , x 2 ^F ) ,..., x d^{F +} ) .

Симплекс задан d +1 вершинами ( i + х< i +        х( i

S   РА ^Х 1 , x 2 ,...,x d Hi = 1, d + 1 .

Каждая грань симплекса S образована d его вершинами, определяющими d -мерную гиперплоскость G i , ( i =1, 2, ..., d +1), описываемую уравнением d

£ a j ) X j + a d + 1 = 0.         (7)

j = 1

Вычислив расстояния от грани G i симплекса S до точки F и до вершины S i этого симплекса, противолежащей данной грани, по формулам

d

£ a j ) x ( F ' + a d' +

S( G i , F ) = ^j"                ,        (8)

£я

• V j = 1

d

£ a j ) x ( i ) + a di + 1

8 G, S i ) = ^j = 1                ,        (9)

d

• . £( a j 7

• \ j = 1

• 2.2.    Разбиение фазовых областей и вычисление равновесных фаз

запишем систему неравенств:

S G,F ) • S ( G i ,S i) > 0, ( i = 1k ) .     (10)

Если все неравенства (10) выполняются строго, то фигуративная точка F , соответствующая ИСК, находится внутри данного симплекса. Если n ( 1 <  n <  d ) неравенств системы (10) обращаются в равенство, то это означает, что фигуративная точка находится на грани d- мерного симплекса (при n = 1), на грани меньшей размерности, являющейся пересечением n граней симплекса (при 1 <  n <  d) или в одной из его вершин (при n = d ).

В соответствии с предложенной последовательностью проверки областей кристаллизации фазовой диаграммы первой рассматривается четырехфазная область кристаллизации трех компонентов: S i , S 2 и S 3 .

Единственным равновесным составом в этой области является нонвариантный раствор E. Три другие твердые фазы, хотя и имеют постоянный состав, но могут присутствовать в донной фазе в самых разнообразных соотношениях. Соединив ее предельными нодами со всеми вершинами солевого основания (равновесными составами твердых фаз), получим четырехфазную область кристаллизации трех солей, геометрическим образом которой является трехмерный симплекс. Поэтому проверка принадлежности фигуративной точки F сводится к проверке принадлежности этой точки симплексу S 1 S 2 S ₃ E .

Если ИСК находится в четырехфазной области кристаллизации трех компонентов: S 1 , S 2 и S 3 (рис. 5), то состав равновесной жидкой фазы является постоянным и соответствует тройному эвтоническому раствору (точка E ), а состав донной фазы - переменным и отвечает точке F S на солевом основании диаграммы. Соотношение твердых и жидких фаз определяется по правилу центра масс или путем последовательного применения правила рычага.

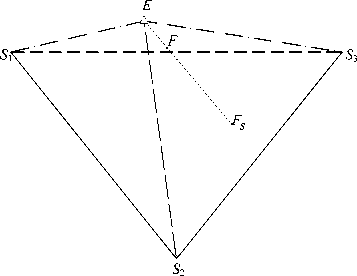
Рис. 5. Моделирование объема совместной кристаллизации компонентов S 1 , S 2 , s 3

Для трех объемов совместной кристаллизации двух солей моделирование сводится к нахождению функциональной зависимости линии моновариантного равновесия, а также к определению принадлежности ИСК данной фазовой области. Линия моновариантного равновесия E ₁₂ E представляется ломаной, составленной из отрезков E ₁₂ M 1 , M i M 2 , ..., M n -1 M n , M n E , где M 1 , M 2 , ..., M n - экспериментальные моновариантные точки на данной линии или вычисленные интерполяционные значения.

Зафиксировав точки S 1 и S 2 , и последовательно взяв по две ближайшие друг к другу моновариантные точки, получим разбиение трехфазной области на тетраэдры S 1 S ₂ E ₁₂ M 1 , S i S 2 M i M 2 , ., S i S 2 M n -1 M n , S i S 2 M n E (рис. 6).

Рис. 6. Моделирование области совместной кристаллизации компо нентов S 1 и S2

Далее решается задача последовательной проверки принадлежности данной фигуративной точки каждому из ( n +1) объемов.

Если ИСК не принадлежит ни одному объему, то он не находится в данной фазовой области. Если же среди полученных объемов будет найден такой трехмерный симплекс S 1 S 2 M i M j , который включит точку F , то равновесная жидкая фаза является решением СЛАУ [2]:

⁽ z j ^- z i ) x L ^{- (} x j ^- x i ) z L = xz j ^- zX j

<( zj - zi) yL - (yj - y,) zL = y.zj - zy       (11),z0xL + z0 yL + (100 — x0 — У0 — z0)zL = 100 z0, где F(x0, y0, z0)   - фигуративная точка,

F L ( x L , y L , z L ) — точка, соответствующая равновесной жидкой фазе, M i ( x i , y, , z i ) и M j ( x j , y j , Z j ) -экспериментальные точки на линии монова-риантного равновесия двояконасыщенных растворов.

По формулам (12) и (13) вычисляется равновесная донная фаза F S ( x S , y S , z S ):

xS

x L^Z 0 ^{- Z}L x 0

^ZL ^{- Z} 0

X s + y S = 100, Z S = 0. (13)

В случае, если фигуративная точка не принадлежит ни одному из частных объемов, проверяется принадлежность данного состава исходной реакционной смеси двум другим областям совместной кристаллизации двух солей, которая проводится аналогичным образом.

После исключения из рассмотрения области кристаллизации трех солей и трех объемов кристаллизации двух солей задача определения фазовой области сводится к следующему: определить, в какой из трех двухфазных областей (объеме кристаллизации компонента S 1 , S 2 или S 3 ) или области ненасыщенных растворов лежит данная фигуративная точка.

Для проверки принадлежности точки F двухфазной области кристаллизации соли S 1 эту область разбивают на треугольные пирамиды. Поверхность кристаллизации представляется в виде "мозаичной" поверхности, построенной как совокупности плоскостей, проведенных по трем ближайшим точкам.

Обозначим множество точек поверхности насыщенных растворов компонентом S1 через M1, M2, ..., Mi, ..., Mn-1, Mn. В первом приближении задача сводится к нахождению ближайших трех точек поверхности насыщенных растворов от точки состава перспективной проекции дан- ной исходной смеси из вершины соответствующего солевого компонента на поверхность насыщенных растворов (рис. 7). В качестве такого критерия "близости" нами был выбран косинус угла между двумя прямыми в трехмерном пространстве (заданными в виде векторов с соответствующими координатами: a ={xa; ya; za}, bi={xb;yb, zb}), определяемый по формуле

F L , как усредненного значения по ближайшим точкам.

cos l a,b

a • b

I al • bl ’

При этом a = S 1 M i , ( i =1, 2, ..., n ), b = S 1 F . Чем меньше угол между прямыми, т.е. чем ближе значение cos ^ к 1, тем ближе находится точка поверхности M i к точке пересечения луча кристаллизации (прямая S i F).

Вычислив значения всех n косинусов, выберем такие три ближайшие к F точки M i , M j и M k , что

• 1)    косинусы соответствующих им углов были наибольшими;

• 2)    эти точки не лежали на одной прямой;

• 3)    эти точки не лежали на одной линии моновариантного равновесия.

3. Вычисление физико-химических характеристик в точках на границе ликвидуса

В случае невыполнения этих условий самая дальняя точка из этих трех заменяется другой, более дальней.

Равновесной твердой фазе соответствует вершина солевого компонента S _1; а равновесной жидкой фазе - точка F L , точка пересечения прямой S ₁ F и плоскости M i M j M k (рис.7).

Если фигуративная точка не принадлежит ни одной из двухфазных областей кристаллизации одной соли, то делается вывод о том, что фигуративная точка находится в области ненасыщенных растворов.

Пусть некоторая фигуративная точка F попала в фазовую область, в которой хотя бы одна из солей находится в твердой фазе. Тогда для нее могут быть вычислены координаты точки, отвечающей составу равновесной жидкой фазы F L ( x ₁, x ₂,., x _k). Эта точка лежит на поверхности ликвидуса.

Если в точках ликвидуса известны физико-химические характеристики (р ), такие как плотность или показатель преломления, то требуется вычислить их и для новой точки -

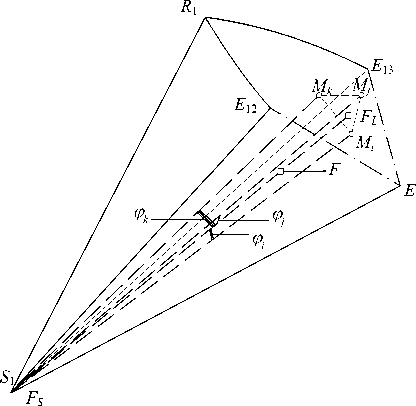
Рис. 7. Определение состава насыщенного раствора при использовании мозаичной модели поверхности кристаллизации

Если точка равновесной жидкой фазы принадлежит v -вариантному геометрическому образу фазового равновесия, то существует такой минимальный v -мерный симплекс S в d -мерном пространстве, которому принадлежит эта точка:

S = { s i ( x ⁽ i ), x 2 ⁱ ),..., x d ), p ⁽ i ) )} i = 1У + . (15)

В каждой вершине этого симплекса известно значение интересующего свойства p . Учитывая v <  d , запишем координаты этих точек в матрицу:

.

X ( v + 1 ) I ^x 1

. (1)

x

v

—

■ ( 2 ) v

v

—

v

p — p ^{( 1 )} p ^{( 2 )}— p ^{( 1 )}

. (16)

X ( v + 1 )

x _v

v

p ( v + 1 ) — p (D J

Приравняв определитель этой матрицы к нулю и выразив p , получим формулу для вычисления заданной характеристики:

p = p(i) — -J1— ^(x — xi(1)R- ,      (17)

A 1, v + 1   i = 1

где A ij - алгебраическое дополнение элемента a ij матрицы A .

4. Визуализация ФДР четверных водно-солевых систем простого эвтонического типа

Приведенное описание геометрической структуры фазовой диаграммы простых эвто-нических водно-солевых систем без образования кристаллогидратов и ограниченных рядов твёрдых растворов позволяет построить объектную модель, программная реализация которой автоматизирует вычисления, связанные с обработкой информации о системе. При этом наглядное представление фазовых диаграмм с числом компонентов до 4 является важной прикладной задачей, поскольку визуальная обработка графической информации играет огромную роль при интерпретации результатов исследований.

Поскольку в настоящее время далеко не все графические библиотеки поддерживают визуализацию в барицентрических координатах, возникла задача графического представления фазовых диаграмм четверных водносолевых систем на основе декартовой системы координат.

Координатным симплексом четверной системы служит трехмерный симплекс – тетраэдр. Его вершины имеют координаты H 2 O (0;0;0), S 1 (100;0;0), S 2 (0;100;0), S 3 (0;0;100). В декартовой системе координат этот симплекс не является правильным, поскольку прямые H 2 O-S 1 , H 2 O-S 2 , H 2 O-S 3 взаимно ортогональны и записаны в ортонорми-рованном базисе:

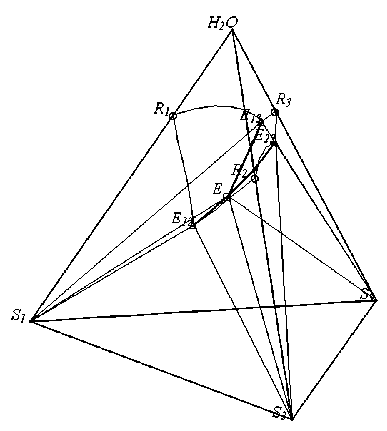
Рис. 8 . Система NH 4 H 2 PO 4 -(NH 4 ) 2 HPO 4 NH 4 Cl-H 2 O при t=20°C

' e i = ( 1,0,0 )

e = у

e ₂

^ e 3 = ( 0,0,1 )

Для того чтобы точки симплекса образовывали правильный тетраэдр, вершиной которого была бы точка H 2 O , а основанием – правильный треугольник A S j S₂S ₃, применяется аффинное преобразование координат, с матрицей T перехода в новый базис:

T =

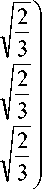
Используя приведенное описание геометрической структуры ФДР и преобразование координат (19) был разработан прототип модуля визуализации четверных ФДР в пакете Wolfram Mathematica 7. Модуль визуализации позволяет строить ФДР четверных водносолевых систем простого эвтонического типа без образования кристаллогидратов и ограниченных рядов твердых растворов по входным экспериментальным данным (рис. 8).

5. Приложение визуализации

Одним из приложений визуализации диаграмм растворимости многокомпонентных водно-солевых систем является подтверждение и проверка открытого недавно коллига-тивного свойства плоскостности линий моно-вариантного равновесия [3-6].

Фундаментальное объяснение свойства плоскостности заключается в преимущественно физическом взаимодействии молекул в растворе [7].

Пример, подтверждающий близость линий моновариантного равновесия к плоскости, построенной на эвтониках оконтуриваю-щих систем, приведен на рис. 9.

Свойство плоскостности используется для прогноза эвтоник по данным об эвтониках окон-туривающих систем, что значительно облегчает планирование эксперимента при изучении этих многокомпонентных систем [8].

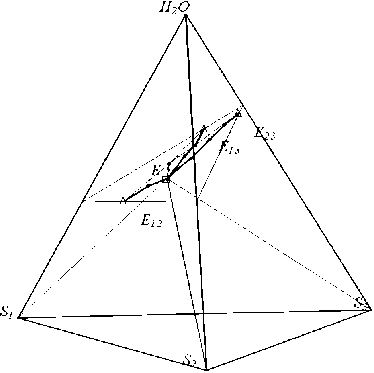
Рис. 9. Плоскость, построенная по оконтуривающим эвтоникам

Заключение

Описанная в статье геометрическая структура фазовых диаграмм позволила создать модуль визуализации фазовых диаграмм четверных водно-солевых систем. Представленный модуль является инструментом для проведения исследовательских работ и решения многочисленных прикладных задач, а также служит образовательным целям.