Гидравлический расчет технологического трубопровода для перекачивания молочных продуктов центробежным насосом

Введение. Центробежные насосы широко используются в технологических линиях по производству молочных продуктов [1–3]. По мнению [1], при выборе центробежного насоса для молочных продуктов (ЦНМП) необходимо учитывать следующие основные факторы: вязкость жидкости и содержание взвешенных веществ в ней; чувствительность характеристик жидкости к сдвигу и диссипации энергии вязкого сдвига, требования к насосу (давление, расход); гигиенические требования и стоимость насоса и эксплуатационные затраты. Необходимо обращать внимание на то, чтобы механическое воздействие насоса в наименьшей степени влияло на характеристики жидкости; насос работал близко к своей оптимальной точке; отсутствовала кавитация; механический износ элементов насоса не приводил к значительной потере эффективности перекачивания [1].

Совершенствованию характеристик ЦНМП посвящен ряд публикаций (см. [4–7]). Известно, что РК ЦНМП оказывает существенное механическое воздействие на дисперсный состав жировой фазы. Результаты экспериментов по оценке влияния конструкций РК на среднее количество жировых шариков молока позволили выделить основные причины потерь: 1) за счет травмирования жира РК, вследствие чего про- исходит налипание на поверхности коммуникаций; 2) снижение жира за счет разрушения оболочек жировых шариков РК и, как следствие, осаждения на внутренних поверхностях коммуникаций после молочного насоса [4].

В [5] была предпринята попытка подобрать профиль лопастей РК ЦНМП, чтобы его воздействие на жировую частицу оставалось величиной постоянной, не превышающей предельного значения. Дальнейшее развитие этого направления исследований ЦНМП представлено в [6]. В [7] была предложена конструкция модернизированного ЦНМП для использования его в качестве смесителя.

Цель исследования – разработка метода расчета гидравлической системы для перекачивания молочных продуктов центробежным насосом с учетом переменной величины разности уровней.

Объекты и методы. В транспортировке жидких молокопродуктов отдается предпочтение НЦМП с открытым РК, несмотря на их меньшую производительность и худшие показатели энергетической эффективности [8–10]. Это связано с легкостью и удобством их разборки и очистки. На рисунке 1 это иллюстрируют фотографии ОНЦ 10/10, характеристики которого будут использованы в данной статье.

а

Рис. 1. Центробежный молочный насос ОНЦ: а – внешний вид; б – открытое рабочее колесо

б

Далее будем рассматривать гидравлическую систему, показанную на рис. 2 (вентили 7 и 8

открыты, 6 и 9 – закрыты). Ее особенностью бопроводе будет нестационарным.

является переменная по времени величина разности уровней H(t), из-за чего течение в тру-

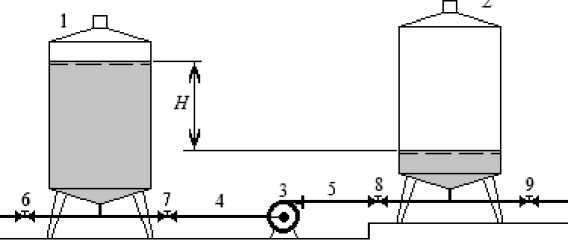
Рис. 2. Гидравлическая схема транспортировки молокопродуктов в технологической линии: 1 – исходная емкость; 2 – конечная емкость;

3 – ЦНМП; 4 – всасывающий трубопровод; 5 – нагнетательный трубопровод; 6–9 – вентили

Рассмотрим систему со следующими параметрами базовой версии технологического трубопровода: рабочий объем резервуаров V 1 = V 2 = 10 м³; их рабочая высота H 0 = 3 м; внутренний диаметр трубопровода d = 35 мм; длина L = 20 м; абсолютная эквивалентная шероховатость Δ = 0,03 мм; суммарный коэффициент местных гидравлических потерь ς М = 4.

Оценим сдвиговую скорость ^γ . Сначала в ЦНМП: диаметр рабочего колеса D= 95 мм; размер осевого зазора δ = 13 мм; частота вращения n = 2900 об/мин = 48,3 об/с; окружная скорость U = 2π · 48,3 · 0,095 = 28,8 м/с. Оценка скорости сдвига в ЦНМП

Y « U/ 6 = 2215 c ¹

Оценим скорость сдвига у стенки трубы для ньютоновской жидкости по формуле

Y = X • W2 /(8v) , где λ – коэффициент гидравлических потерь по длине трубопровода.

При расходе молочных сливок от 2 л/с и выше сдвиговая скорость будет более 2000 с –1.

Опубликовано большое количество работ, в которых приводятся данные о реологическом поведении молока и сливок при высоких скоростях сдвига (см. [11–13]). Общее мнение, что при скорости сдвига более 500 с-1 молочные сливки жирностью 20% и менее можно считать ньютоновскими жидкостями. Далее будем рассматривать жидкости, которые можно считать ньютоновскими (вода, молоко, сливки жирностью менее 20 %).

Полагаем, что в гидравлической системе на рисунке 2 выполнены условия отсутствия кавитации. Режим течения жидкости - турбулентный. Давление на поверхности жидкости обоих резервуаров - атмосферное. Постановка задачи, кроме дифференциального уравнения для объема перекачиваемой жидкости V , требует задания начального условия:

dV/dt = Q , V (0) = 0, Q = WS о ,      (1)

L dQ gS 0   ^dt

= H p ( Q ) + H ( t ) - b • Q

где L - общая длина трубопровода; ^g - ускорение свободного падения; H p - мгновенное значение напора насоса; H - текущая разность уровней; Z - коэффициент гидравлического сопротивления сети.

Z = ^{л L} + Z f «i ^л = ^0,11 • d_i

, где Д - эквивалентная шероховатость трубопровода; Z Mi - коэффициенты потерь в местных гидравлических сопротивлениях; ^v - коэффициент кинематической вязкости жидкости; Re - число Рейнольдса.

где Q , W - объемный расход и скорость жидкости в трубопроводе соответственно; t - время; S о = п d ²/4 - площадь поперечного сечения трубопровода; d - его внутренний диаметр.

Полагаем, что на всем протяжении потока скорость движения жидкости одинакова и плавно изменяется по времени. Тогда нестационарное уравнение Бернулли также представляет собой дифференциальное уравнение первого порядка [14] (с начальным условием Q (0) = 0):

b = tsi , ⁽²⁾

Коэффициент гидравлического сопротивления сети рассчитывался с использованием известной формулы Альтшуля:

0,25

Д 68 I    „ W • d

1+ F I Re = d Re)

,,

Зависимость напора H p ( Q ) в уравнении (2), а также затраченной мощности ЦНМП от подачи аппроксимируем многочленами:

H p = f i ( Q )= a 0 + a 1 Q + a 2 Q ², N = f 2 ( Q ) = c 0 + c 1 Q + c 2 Q ², + c 3 Q ³,

где размерные эмпирические коэффициенты определяются для заданного ЦНМП по рабочим характеристикам методом наименьших квадратов.

Результаты и их обсуждение. В качестве примера в данной статье используем рабочие характеристики молочного насоса с открытым рабочим колесом ОНЦ 10/10 (показаны точками на ри- сунке 3, получены для воды при 20 °С) [15]. Коэффициенты в формулах (4) будут a0 = 23,35 м; ai = -1,479 м/(дм3/с); a2 = -0,228 м/(дм3/с)2; c0 = 0,292 кВт; ci = 0,840 кВт/(дм3/с); c2 = -0,172 кВт/(дм3/с)2; c3 = -0,0134 кВт/(дм3/с)3. Видно, что результаты расчета по формулам (4) хорошо согласуются с экспериментальными данными.

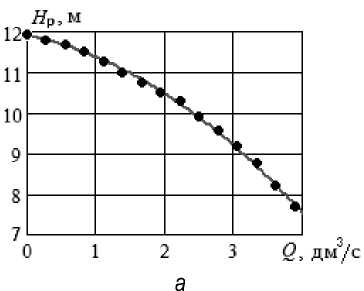
Рис. 3. Рабочие характеристики насоса ОНЦ 10/10: a – напор; б – затраченная мощность. Точки – данные испытаний [15], линии – результаты расчета по формулам (4)

б

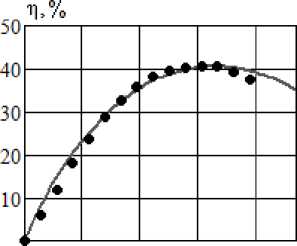
В технической документации [15] приведена и Пересчитаем КПД по данным испытаний напора зависимость КПД от подачи (точки на рис. 4, a ).   и мощности (рис. 3) по формуле

П = Ф й ) = 100 • ^ w gHQ = 100 • p . g ■ Q ■ ^, N                  ^f 2 ^{( Q} )

где ρ w – плотность воды.

Рисунок 4, a показывает, что в технической документации [15] КПД практически не отлича- ется от результата расчета по графикам напора и мощности.

б

a

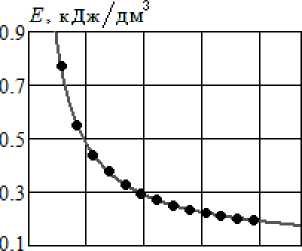
Рис. 4. Показатели энергетической эффективности насоса ОНЦ 10/10: a – КПД; б – удельная затраченная работа. Точки – по данным испытаний [15], линии – результаты расчета по формулам (5) и (6)

Для оценки энергетической эффективности насосных систем успешно применяют показатель удельных энергозатрат (например [16]):

E = N / Q . (6)

Показатель E , рассчитанный для перекачивания воды, приведен на рисунке 4, б. Как и в [16], величина E снижается при увеличении подачи выше номинального значения, тогда как КПД ухудшается. Разумеется, подача не должна выходить за правую границу рабочей области, иначе могут снизиться другие показатели работы насоса.

Необходимо учесть отличие свойств жидких молокопродуктов от аналогичных параметров воды. Имеющаяся методика [17] позволяет вы- полнить оценку влияния этих свойств для ньютоновских жидкостей. Заметим, что изменение характеристик ЦНМП при перекачивании обезжиренного молока столь мало, что его можно не учитывать в инженерных расчетах.

В качестве примера рассмотрим сливки молочные жирности 18 % при температуре 20 °С с плотностью ρ = 1011 кг/м³, коэффициентом кинематической вязкости ν = 8,22 · 10^–6 м²/с = 8,22 сСт [11], частота вращения рабочего колеса ЦН n = 2900 об/мин. По рисункам 3 и 4 при перекачивании воды с наибольшим КПД η 0 w = 0,406; Q 0 w = 11,88 м³/час; H 0 w = 8,75 м; N 0 w = 0,698 кВт. По формулам [17, с. 8] рассчитаем значения аналогов числа Рейнольдса и коэффициента быстроходности:

n

, ₌ 3/ g o w² • n ₌311Й900

^q       ν             8 , 22

n  Q w  '5

1 3600 J

2900 •

11 , 88 A ⁰ ' 5

3600 J

q

H

0 , 75 0 w

8 , 75 ^{0 , 75}

= 32 , 75 .

Вспомогательный параметр

B =       16 ,5      =         ¹⁶ , 5         = 2 , 92

12 60 - n q ■ ^Re q   ^l2 60 • 32 , 75 • 400

Поправочные коэффициенты

C H = C Q = exp [ - 0 , 165 - ( log B ) ³ ' ¹⁵ ] = 0 , 985 ; C _n = B ^{- 0 , 0547}' ^{B 0,69} = 0 , 885 .

По формулам (10), (11) оценка снижения напора и подачи всего 1,5 %, а КПД – 11,5 %: η0= 0,359; Q0 = 11,71 м3/час; H0 = 8,62 м, откуда с учетом увеличения плотности затраченная мощность возрастет до N0 = 0,787 кВт. Следователь- но, показатель удельных энергетических затрат увеличится на 14,4 % – с 0,211 до 0,242 кДж/дм3.

Результаты расчетов представлены на рисунках 5–8.

a

б

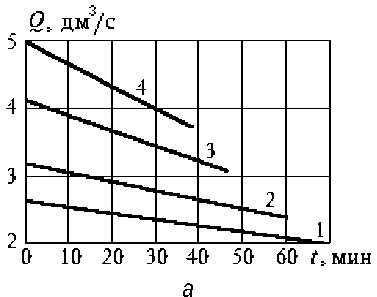
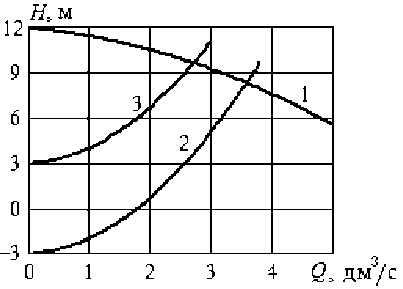
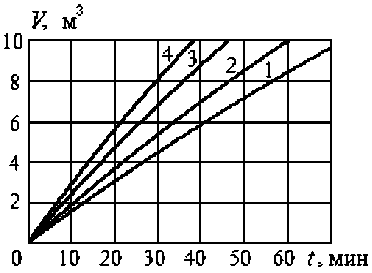
Рис. 6. Динамика перекачивания сливок насосом ОНЦ 10/10 при L=20 м, H(0)=3 м и различных диаметрах трубопровода: 1 – d = 32 мм; 2 – d = 35 мм; 3 – d = 40 мм; 4 – d = 45 мм; a – изменение расхода по времени; б – объем перекачанной жидкости

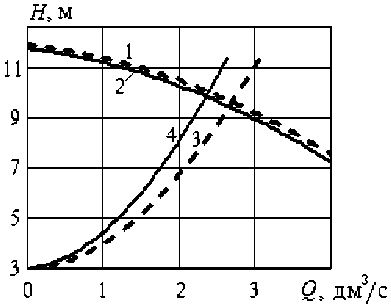
Рис. 5. Рабочая точка насосной установки ОНЦ 10/10 при H(0) = 3 м, L = 20 м, d = 35 мм: a - вода ( 20 °С) ; 1 - напорная характеристика насоса; 2 - характеристика трубопровода в начале перекачивания; 3 – в конце перекачивания; б – вода и сливки; 1, 2 – напорная характеристика насоса (1 – вода, 2 – сливки); 3, 4 – характеристика трубопровода в конце перекачивания (3 – вода, 4 – сливки)

б

б

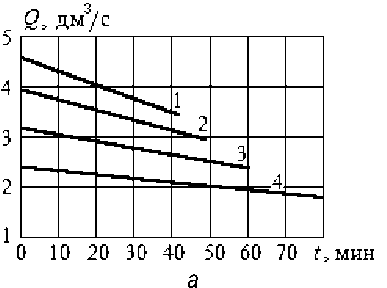
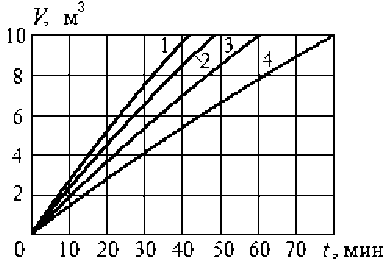
Рис. 7. Динамика перекачивания сливок насосом ОНЦ 10/10 при d = 35 мм, H(0) = 3 м и различной длине трубопровода: 1– L = 5 м; 2 – L = 10 м; 3 – L = 20 м; 4 – L = 40 м; a – изменение расхода по времени, б – объем перекачанной жидкости

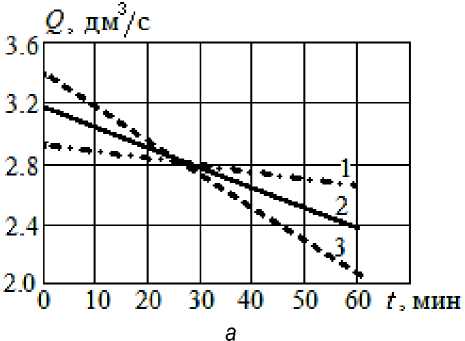
Рис. 8. Динамика перекачивания сливок насосом ОНЦ 10/10 при d=35 мм, L = 20 м и различном перепаде уровней: 1– H(0) = 1 м; 2 – H(0) = 3 м; 3 – H(0) = 5 м;

a – изменение расхода по времени; б – объем перекачанной жидкости

По рисункам 6, а, 7, а, 8, а снижение расхода близко к линейной зависимости. Поэтому можно предложить инженерный метод расчета, без решения дифференциальных уравнений численным методом. Определить расход в начальный и конечный момент перекачивания (Q0 и QК), по ним среднее значение QС = 0,5 (Q0 + QК), приближенное значение времени перекачивания TС = V/QC. Отличие от значения времени перекачи- вания, полученного из решения системы дифференциальных уравнений TК, менее 0,5 %.

По рисунку 8, а увеличение H (0) заметно влияет на Q 0 и Q К , при этом среднее значение Q С изменяется незначительно. Поэтому время перекачивания на рисунке 8, б почти не изменяется.

Зная зависимость расхода от времени, можно найти полезную (гидравлическую) A u , и затраченную работу A z на перекачивание жидкости:

T K                                T K

A u = g ■ P - J Q ^T ) • ^f 1 ⁽ Q ^{( t} )) d ^T ., A z = j ^f 2 ⁽ Q ( ^T )) d ^T .

0                                          0

В функциях H = f1(Q), N = f2(Q) необходимо     Результаты расчета параметров гидравли- учесть вышеуказанную поправку на вязкость ческой системы представлены в таблице. сливок.

Результаты расчета параметров гидравлической системы

d, мм	L , м	Q 0, дм3/с	Q К , дм3/с	T К , мин	A u , кДж	A z , кДж	E , кДж/м3	η, %
35	5	4,57	3,43	41,7	721	2144	214,4	33,6
35	10	3,93	2,94	48,5	820	2337	233,7	35,1
35	20	3,17	2,76	60,4	923	2663	266,3	34,6
35	40	2,39	1,78	80,0	1009	3184	318,4	31,7
32	20	2,61	1,95	73,2	986	3006	300,6	32,8
35	20	3,17	2,76	60,4	923	2663	266,3	34,6
40	20	4,10	3,06	46,6	796	2284	224,4	34,8
45	20	4,97	3,71	38,4	656	2051	205,1	32,0

Заключение. С увеличением длины трубопровода растет его гидравлическое сопротивление. Расход жидкости заметно падает. Если L = 5 м, то время перекачивания менее 42 мин, а при 40 м оно увеличивается до 80 мин. При этом показатель энергетических затрат на перекачивание сливок монотонно возрастает с 214,4 до 318,4 кДж/м³.

С увеличением диаметра трубопровода снижается его гидравлическое сопротивление. Расход жидкости заметно растет. Если d = 32 мм, то время перекачивания более 73 мин, а при 45 мм оно уменьшается до 34,4 мин. При этом показатель энергетических затрат на перекачивание сливок снижается с 300,6 до 205,1 кДж/м³. Разумеется, увеличение диаметра трубопровода ограничено стоимостными показателями. Для чего необходимо решать оптимизационную задачу, как, например, в [18]. Но это предмет отдельного исследования.

Заметим, что в обоих случаях КПД, в отличие от показателя E , изменяется не монотонно, но совсем незначительно. Подбор насосного оборудования по КПД производить нецелесообразно, следует опираться на показатель E .