Гидродинамика процесса охлаждения молочной сыворотки при поточной кристаллизации лактозы

Поточная кристаллизация лактозы развивается в сложных гидродинамических условиях и широком температурном диапазоне для молочной сыворотки. [1, 5, 6]. Для технической реализации поточной кристаллизации лактозы в ГНУ ВНИИ молочной промышленности Рос-сельхозакадемии, разработана опытнопромышленная установка (рисунок 1). Основной частью этой установки является пластинчатый скребковый теплообменник, который используют как охладитель-кристаллизатор.

Молочную сгущённую сыворотку с температурой 55-60 °С подают насосом в первую секцию пластинчатого скребкового теплообменника, где она охлаждается до температуры массовой кристаллизации лактозы, затем поступает в дисковый обработник, состоящий из набора подвижных и неподвижных дисков.

Рисунок 1 - Схема установки для поточной кристаллизации лактозы в молочной сыворотке: 1-приёмная ёмкость, 2-насос подачи продукта, 3-пластинчатый скребковый теплообменник, 4- I секция охлаждения, 5- II секция охлаждения, 6-дисковый обработник, 7-щит управления, 8-ёмкость для затравки, 9-насос-дозатор, 10-термометры сопротивления, 11-манометр с разделительной мембраной, 12-струйный смеситель, 13-буферная ёмкость.

Подвижные диски снабжены выступами со специальными проточками, обеспечивающими кавитационный режим течения. Перед дисковым обработчиком в поток продукта через струйный смеситель насосом-дозатором впрыскивается взвесь затравки, которая диско

вым обработчиком гарантированно распределяется по всему объёму продукта, при этом подвергая его интенсивному гидродинамическому воздействию. Охлажденный во II секции теплообменника до конечной температуры продукт поступает в буферную ёмкость и затем на фасовку.

Авторами проведено исследование гидродинамика охлаждения молочной сыворотки при поточной кристаллизации лактозы в пластинчатом скребковом теплообменнике. [1,5-6]. Такой аппарат представляет собой набор чередующихся теплообменных и так называемых продуктовых пластин в форме диска, установленных и зажатых на специальных штангах. Набор последовательно соединенных теплообменных элементов образует теплопередающую поверхность аппарата для нагревания или охлаждения продукта. В зависимости от организации процесса молочная сыворотка может поступать в пространство между дисками как из центрального отверстия, так и из отверстий, расположенных на периферии дисков.

Внутри продуктовых пластин расположены подвижные диски, закрепленные на валу. С обеих сторон этих дисков подвижно закреплены полиамидные ножи специальной формы. При вращении дисков эти ножи счищают с поверхности теплообменных пластин пристенный ламинарный слой обрабатываемого продукта, при этом происходит его перемешивание. В зависимости от направления движения молочной сыворотки и хладоносителя аппарат может рабо тать по схеме прямотока и противотока.

Исследование основано на решении дифференциального уравнения теплопереноса в движущихся жидких средах, записанных в цилиндрической системе координат при осе симметричном распределении температуры, без учета диссипации энергии:

д T

Vr — + Vz д r д T

д z

(д2 T 1 д T д2 T ), a . ++ 2- v д r2 r д r дz2 v

где T - температура в точках продукта, оС, r и z - цилиндрические координаты точки продукта, vr и vz - проекции скорости точек продукта на оси r и z, а - коэффициент температуропроводности.

Расчётная схема процесса приведена на рисунке 2.

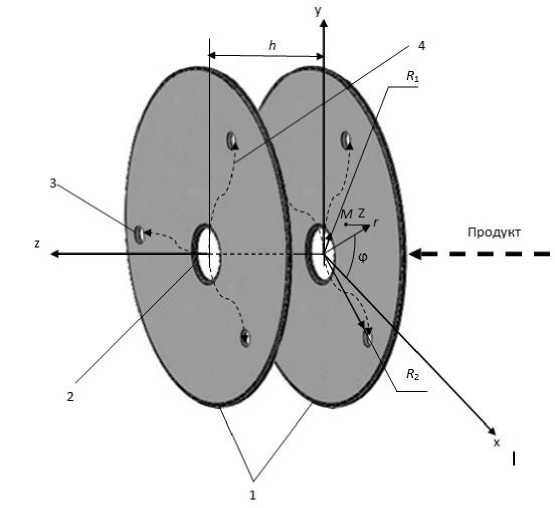
Рисунок 2 - Расчётная схема: 1 - продуктовые пластины; 2 - центральное отверстие; 3 - периферийные отверстия; 4 - линии тока продукта

Полагаем, что осевая скорость продук -та v _z значительно меньше радиальной v_r и окружной v ^ скоростей, поэтому в уравне- д 7

нии (1) v —® 0 положим. Для определения z дz радиальной скорости vr воспользуемся дифференциальным уравнением стационарного осесимметричного течения несжимаемой нелинейно-вязкой жидкости, полагая в нем реологические константы и плотность продукта р не зависящими от температуры для данной пары дисков (охлаждающего элемента). Для этого запишем общее дифференциальное уравнение осесимметричного стационарного течения сплошной среды в напряжениях [2] в проекции на радиальное направление г:

Интегрируя уравнение (5), находим:

v r = ¹ f ⁽ z ) . r

д vr      дv r vr — + v, — дr     дz

—

v ²

— ^ = F_r +

r

На основании равенства (6) для интенсивности скоростей деформации H из (4) получим выражение:

₊1 Р ^т„ । ^{д т} „ ₊ ^T rr ^{— т} фф p  д r     д z      r

H =r fz ) 1 +( f s Г     ⁽⁷⁾

у у r ) у 2 r )

где T _rr , т _фф - нормальные напряжения на

площадках перпендикулярных соответственно

радиальной r и окружной ф осям, T _rz - касательное напряжение на площадках перпендикулярных осям r и z .

Реологические исследования молочной сыворотки позволяют с большой точностью принять в качеств е её реологической модели степенную модель Оствальда-Де Виля. Для такой модели компоненты тензора напряжений, входящие в уравнение (1), при сделанных ранее предположениях имеют вид [3, 4]:

Tr =— Р + 2 kM—1   , д r т„ = — Р + 2k\H\"—1 vr-, ,         (3)

т„ = kH дz где k и n- реологические константы молочной сыворотки, H - интенсивность скоростей деформации равная:

где штрих во втором слагаемом подкоренного выражения и далее означает производную по координате z .

Оценим порядки слагаемых в подкоренном выражении формулы (7), приведя ее к безразмерному виду. Для этого запишем следующие соотношения между размерными и безразмерными величинами, входящими в (7): z = z h ,

r = r R 2 ,

f ^{( z} ) = v r ^R 2 Ж) ,        ⁽⁸⁾

f'(z ) = vR    , где в качестве характерных координат взяты: зазор h между дисками и радиус R2 центров выходных отверстий (рисунок 1); маленькая

дуга над v r означает осреднение по координа

те r , а верхняя черта обозначает безразмерную величину. Подставив выражения размерных величин по соотношениям (8) в формулу (7), приведем ее к виду:

H =

д v r

vr r

и vr h

H = х

r

д r

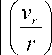
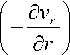
х

J [ fz ) ] ² h 2 +[ ® 1 ² у у r ) ^R 2 у ² )

1 ( д v_r + — I —-

4 У д z

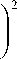
Величина k|H|” ¹ может рассматриваться как некоторая кажущаяся (эффективная) вязкость.

Уравнение неразрывности (несжимаемости) справедливое для любой жидкой среды при сделанных предположениях имеет вид:

И rv r ) = ₀. д r

Так как в формуле (9) подкоренное выражение приведено к безразмерной форме, то порядки слагаемых в этом выражении будут определяться порядком коэффициентов при этих слагаемых. Коэффициент при первом слагаемом значительно меньше коэффициента при втором слагаемом, т. е. __ << _• Так, R 22    4

например, если положить h ~ 10 ^{— 3} м и

„               h ²   „ _

R ₂ ~10 м, то--0,01. Таким образом, в

R 2 ²

подкоренных выражениях (9) и (7) можно оставить только вторые слагаемые. На этом основании интенсивность скоростей деформации (7) запишется как:

H =

2 r

= i f 'И .

2 r

но пренебречь по сравнению с давлением p . Это следует из условия малости угловой скорости to вращения мешалок. Так, например, в реальных охладителях данного типа p ~ 10 5 Па , to ~4 c ¹, r ~ 0,1 м , р ~10 ³ кг/м ³ . Отсюда

В этом случае с учетом (6) соотношения (3) примут следующий вид:

следует справедливость усиленного неравенства, написанного выше. На этом основании уравнение (13) запишется как:

T rr = - P - 2 k

f'(-z) ”-" f (z)

2 r

2     ^,

r

rn

” -1

х

.

^т ФФ = ^- p + ^{2 k}

f '(z) ”-1f (z)

2 r

2     ^,

r

.

т = к rz

f '(z ) ” ^-1 f ' ( z )

2 r

r

Так как продукт принудительно вращается при помощи крестообразных лопастей, то окружная скорость точек продукта не больше величины to r , где to - угловая скорость лопастей мешалки. Поэтому примем эту величи

ну за окружную скорость v ^ , т. е.:

х4[( f,(z)) n] signf,(z) 5z

При этом считается, что давление p не зависит от поперечной координаты z. В дальнейшем, в силу симметрии профиля радиальной скорости относительно срединной плоскости дисков, будем при гидродинамических расче-h тах рассматривать область 0 < z < —. Для этой области sign f'(z )= 1. Приравнивая левую и правую части (14) к одной и той же константе A с учетом sign f'(z) = 1, получим два обык-

V _v = ^{to r} . (12)

Подстановка выражений компонент тензора напряжений из (11) и окружной скорости (12) при условии v « 0 в уравнение (2) приводит это уравнение к следующему виду:

[f (z )Г _ 1 '

r3       р д r новенных дифференциальных уравнения сительно функции f (z) и давления p :

отно-

rn dp (P )= A.        (15)

5 r

k f1) — [(f‘(z))” ]= A • (16) к 2 J 5zL J

Уравнения (15), (16) будем решать

P -

к

2 2 к

2 7

+

при следующих граничных условиях:

1 Г к ” ^-1 С 1 к ” п

k I 1 I I 1 I 5+ — I - I 1-1 — х

р к 2 J к r 7 5z

^{х [ ( f} '^{( z} )) ” ^] signf '( ^z )

^r = R 1 , P ⁽ R 1 ) = P 1 ;

r = R2, P(R2) = P2,      (17)

z = 0, f (r, 0)= 0;

z = -, f 'fr, h) = 0,       (18)

2 к ,2 J

Выражение в левой части равенства (13) значительно меньше каждого из слагаемых в его правой части. Это следует из оценок, сделанных аналогично оценкам в формуле (7).

Тогда можно принять

[ f ( z ) ] ²

r ³

~ 0 и в полу

чившемся уравнении разделяются слагаемые, зависящие только от соответствующих координат r и z. Кроме того, в первом слагаемом 2 2

правой части величина ^р ----<< p и ей мож- 2

где R2 - расстояние центров выходных отверстий от центров дисков; последнее из граничных условий (18) следует из симметрии профиля радиальной скорости относительно сре-h динной плоскости z = —. Интегрированием уравнений (15) и (16) при граничных условиях (17) и (18) получаем выражения для давления p (r ) и функции f (z):

Р ⁽ r ) = P i - p ^P1 _ p 21-

^R 2 R i

x ( r ^{l —} " - R 1 ^- ' )

f ( z ) = —

⁽ P i — P 2 ^{)( l} — n ) 1 n k ( R 2 ^{- n} - R ^{1 — n} )

n

X---- n + l

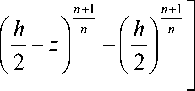
Для полного гидродинамического расчета охладителя представляется важным получить зависимость между перепадом давления p 1 — p2 на входе и выходе продукта из данного охладительного элемента и расходом продукта h q , используя формулу

q = 4 п r J v r dz .

2 n <  h q = 2 п h -----1 —

2 n + П 2

Подставив в эту формулу выражение v _r c учетом (20) и интегрируя, получим:

n +l

n

X

. (21)

(Pl - P 2 )(l - 1) 1 n k (R 2-n - Rin)

Таким образом, полученные формулы позволяют проводить гидродинамический расчет пластинчатых скребковых теплообменных аппаратов при охлаждении молочной сыворотки для кристаллизации в ней лактозы.