Границы применимости метода геометрической оптики для задачи рассеяния света на шестигранных ледяных пластинках перистых облаков

В настоящее время решение задачи рассеяния света на ледяных кристаллах перистых облаков удается получить с разной степенью точности и эффективности как на основе точного решения уравнений Максвелла, так и с использованием приближений физической и геометрической оптики [1]. Очевидно, что использование приближенных методов позволяет более эффективно получать решение, однако, остро встает вопрос о границах применения данных приближений. В работе используется приближение физической оптики для оценки границ применимости геометрической оптики.

К настоящему времени проведено большое количество экспериментальных работ посвященных исследованию входящих в состав перистых облаков кристаллических ледяных частиц. В частности установлено, что для гексагональных ледяных пластинок справедливо соотношение h = 2.02 D °'449 (1)

где h – толщина и D – диаметр частицы.

Пространственная ориентация частиц в облаке может варьироваться от полностью хаотической, до ярко выраженной преимущественной [2]. В данной статье пространственная ориентация частицы задается тремя углами Эйлера – α , β , γ , и предполагается, что частицы в облаке равномерно распределены относительно углов α и γ , а распределение частиц по углам наклона β подчиняется Гауссовому распределению.

Основной вклад в направление назад от гексагональных ледяных частиц вносится двумя качественно различными типами траекторий и может быть мысленно разделен на зеркальную и уголковую компоненты рассеянного света [3]. Зеркальная компонента, в свою очередь, может быть разделена на внешнюю , и внутреннюю .

Как уже было показано [3], для случая вертикального зондирования ледяных пластинок, уголковой

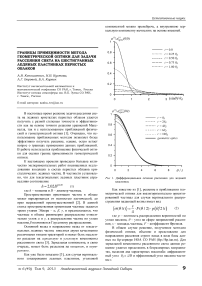
Рис 1. Дифференциальное сечение рассеяния для ледяной пластинки.

Как известно из [1], решение в приближении геометрической оптики для квазигоризонтально ориентированной частицы для случая вертикального распространения падающей волны имеет вид

(CT(9|t» = ^ ■ F (9 /2) ■ p (9/ 2|t) (2)

где p – плотность распределения вероятностей по углам наклона, θ – угол на сфере направлений рассеяния, s – площадь частицы, F – коэффициент Френеля.

В общем случае решение, полученное методом физической оптики, объемно и представлено для направления рассеяния строго назад в виде базы данных на ftp-сервере ИОА СО РАН ( ftp://ftp.iao.ru ). Для зеркальной компоненты рассеянного света данное решение удается представить в безразмерных координатах, выделив два характерных масштаба: дифракционный угол θ_d = λ / D и эффективный угол наклона частицы t .

Для малых углов флаттера, когда t <<  θ_d , характерным масштабом на сфере направлений рассеяния является дифракционный угол θ_d . Дифференциальное сечение рассеяния <  Г >  в данном случае удобно пронормировать на величину ДСР в нуле для строго горизонтально ориентированной частицы, которая определяется выражением

,                ,                 V2

Г spec ( 0|0 ) = г ( 0|0 ) = F (0) -у   ⁽³⁾

л

Из рисунка 1, видно, что при увеличении угла флаттера ДСР постепенно теряет вид дифракционной кривой, переходя к виду функции p( в 1 1 ) .

Для больших углов флаттера, когда t >> θd, характерным масштабом на сфере направлений рассеяния является эффективный угол t. Дифференциальное сечение рассеяния < Г > в данном случае удобно пронормировать на величину ДСР в нуле для геометрической оптики, посчитанную при заданном t, которая определяется выражением о£ (0|t ) = F (0) p (0|t)     (4)

Как видно из рис. 1, граница применимости геометрической оптики при наличии флаттера определяется соотношением величины флаттера к угловому размеру дифракционного кольца (рис. 1). Полученный результат может быть полезен для обоснования применимости метода геометрической оптики.

Работа выполнена при финансовой поддержке РФФИ (грант № 12-05-00675а, 13-05-90774мол_рф_нр).