Границы законов распределений показателей надёжности машин

Изучение надёжности техники в реальных условиях эксплуатации даёт основу для объективного планирования производственной деятельности. В свою очередь, обоснованная методика сбора и обработки информации позволяет сделать достоверные выводы об изучаемом процессе. Существующие теоретические и практические методики дают возможность определить устойчивые математические закономерности проявления отказов машин. Случайность и зачастую внезапность возникновения неисправностей технических систем предопределяет также вероятностную оценку достоверности этих событий. На основе теории вероятностей устанавливают математические закономерности проявления отказов машин, которые аппроксимируются соответствующими функциями. Для этого применяются законы распределения случайных величин, каждый из которых имеет свою область употребления, но обеспечивающих абсолютное совпадение с экспериментальными данными в настоящее время нет [1]. При анализе работоспособности машин, как правило, используются нормальный (ЗНР), Вейбулла (ЗРВ), Релея (ЗРР) и экспоненциальный (ЗРЭ) законы распределения, диапазон предварительного приложения их осуществляется по коэффициенту вариации случайных величин. Возможности логнормального распределения (ЛНР) в исследовании надёжности установлены не полно, известно лишь описание времени безотказной работы некоторых объектов. В данном случае предполагается, что если случайная величина распределена по ЛНР закону, то логарифм её по любому основанию будет распределён по нормальному закону. Эта функция предназначена для описания совокупного действия многих равнозначных факторов, когда перемены выходного показателя примерно пропорциональны изменению самих факторов. Кривые распределения имеют асимметрию и эксцесс, математическое ожидание, мода и медиана не совпадают.

Для анализа взяты выборки информации по отказам систем и механизмов зерноуборочных комбайнов с различной степенью их рассеивания [2]. Далее было проведено последовательное, попарное сравнение законов распределения. Выявлено, что при коэффициенте вариации V = 0,25 отклонение логарифмически-нормального распределения от опытных точек больше, чем нормального (рис. 1).

Рис. 1. Дифференциальные функции ЗНР и ЛНР

При этом относительная ошибка определения среднего показателя для ЗНР – 2,6%, ЛНР – 7,2%. При сравнении с зако- ном Вейбулла (V = 0,5) ошибки соответ ственно равны 3,7% и 6,1% (рис. 2).

Рис. 2. Вероятность плотности отказов при ЗРВ и ЛНР

Переход в зону действия закона Релея (V = 0,75) показывает, что аппроксимация распределением ЛНР также менее точна, погрешности составляют 3,9% и 6,8% (рис. 3).

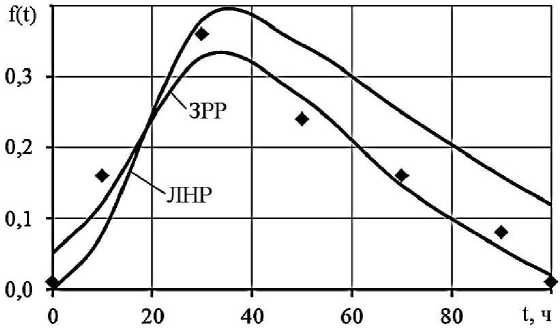
Рис. 3. Распределение отказов при ЗРР и ЛНР

Как видно из рисунка 5 при экспоненциальном характере отказов (V = 0,75) логнормальная функция не приемлема, ошибки расчёта в данном случае 2,2% и 9.7%.

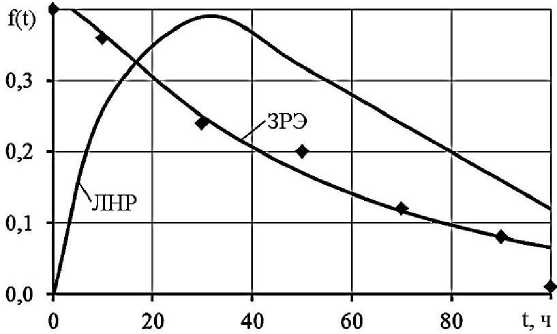
Рис. 4. Функции распределения отказов при ЗРЭ и ЛНР

На основе критерия Пирсона была выполнена оценка вероятности совпадения опытных и теоретических данных (рис. 5).

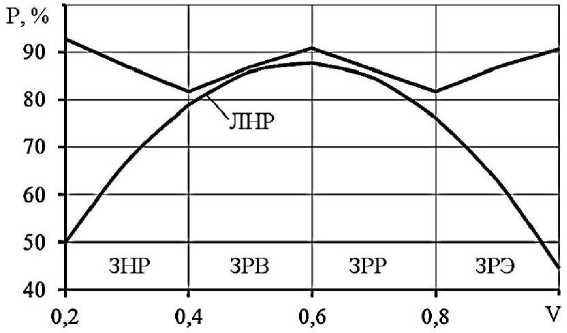
Рис. 5. Точность аппроксимации эмпирических распределений

Установлено, что наивысшая точность логарифмически-нормального распределения достигается при коэффициенте вариации 0,5…0,7. Следовательно, при назначении целевой функции описания безотказ- ности объектов в этом диапазоне целесо образно рассматривать по критериям со гласия одновременно три закона: Вейбул ла, Релея и логнормального.