Гребневая модель прогноза половозрастной структуры детей и молодежи

Источник: РОССТАТ. Демографический прогноз до 2030 года. Численность населения по отдельным возрастным группам //

Рис. 1. Прогноз (средний вариант) численности населения по отдельным возрастным группам (на начало года, тыс. человек)

Основная задача при построении Гребневой модели (далее Ридж модель) возрастной структуры детей и молодежи —разработка подхода, основанного на эконометрическом моделировании и позволяющего более точно увязывать структуру демографической динамики с изменениями в системе образования.

Предлагается новый инструментарий, позволяющий с определенной долей вероятности оценить количество детей и молодежи в определенной когорте на различных уровнях образования. Это дает возможность моделировать количество мест в до- школьных учебных заведениях, в школах, в системе СПО и ВПО. Для построения Ридж модели следует учесть специфику демографической динамики: рождение детей, изменение половозрастной структуры на различных уровнях российской системы образования.

В нашем подходе будет применен анализ статистических данных по различным когортам детей и молодежи, на основе которого выстраивается регрессионная зависимость между показателями рождаемости и возрастной структурой в детских са- дах, школах и профессиональном образовании.

Сегодня это особенно актуально для всех учебных заведений, так как реализуется программа подушевого финансирования. Основным критерием «эффективности образовательного учреждения» является наполняемость классов и групп: количество детей не должно быть меньше 25 человек. Таким образом, возникает объективная необходимость в разработке специального подхода к процессу планирования бюджетных и внебюджетных мест в учебных заведениях.

Данную задачу можно осуществить на основе Гребневой модели, которая позволит с определенной долей вероятности предопределить ожидаемое количество учащихся на всех уровнях обучения.

Реализация и построение модели заключается в следующем: на основе данных РОССТАТа [4] формируется когортная выборка учащихся. Для соблюдения правила репрезентативности целесообразно выделить следующие возрастные категории: 1) дети до 1 года;

• 2)    рождение с учетом смертности в

• 1    год (1 год);

• 3)    дошкольный возраст (ясли и детский сад) (3 года);

• 4)    начальная школа (7 лет);

• 5)    старшие классы или СПО (16 лет);

• 6)    вуз (18 лет).

Выбор данных групп обусловлен следующим: первая — это «Дети до 1 года» — предусматривает статисти- ческий анализ и учет динамики детей в данном возрасте.

На рис. 2 представлена их численность с 1990 по 2013 гг.

Вторая группа учитывает смертность до года, т.е. выборка осуществляется из всех детей которые на данный момент были в возрасте от 0 до 1 года. Из рис. 2 и 3 видна положительная динамика.

Третья группа анализирует «потенциальных» детей, которые могут претендовать на место в детских садах. В 2013 г. их количество на 222 тыс. больше, чем в 2010 г. (рис. 4).

Четвертая группа — это учащиеся начальной школы. Как видно из данных (см. рис. 5), прирост количества детей в этом возрасте замедлился и остановился на уровне 1,6 млн. человек.

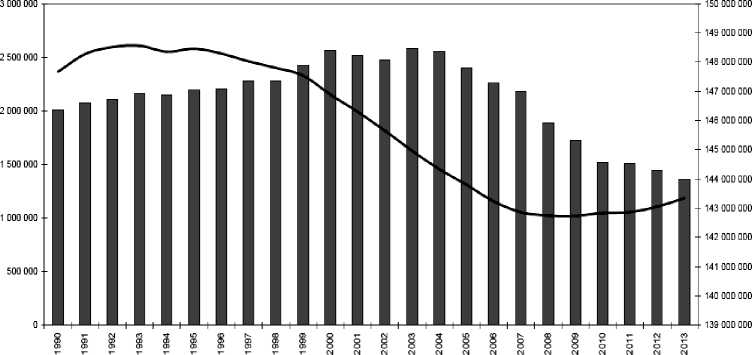
Учащиеся старших классов или студенты среднего профессионального образования (СПО) учитываются в пятой группе (рис. 6).

В отличие от предыдущей, видна тенденция к сокращению (1,36 млн. человек). Это является последствием «демографической ямы». Однако, учитывая рост численности в предыдущих когортах, в дальнейшем можно ожидать положительную динамику в старших классах.

Деление внутри категории на тех, кто учится в СПО или продолжает обучение в школе происходит, исходя из долевого деления в предыдущие моменты наблюдения.

Последняя шестая категория представлена потенциальными претендентами в высшие учебные заведения (рис. 7).

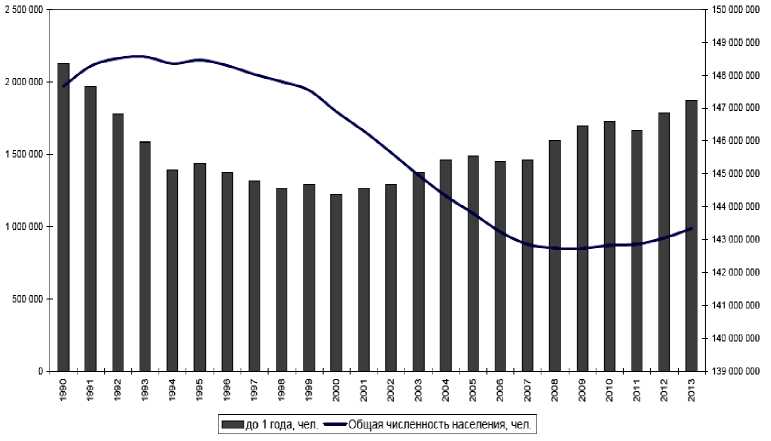
Рис. 2. Численность населения РФ на 1 января по категории «Дети до 1 года», человек

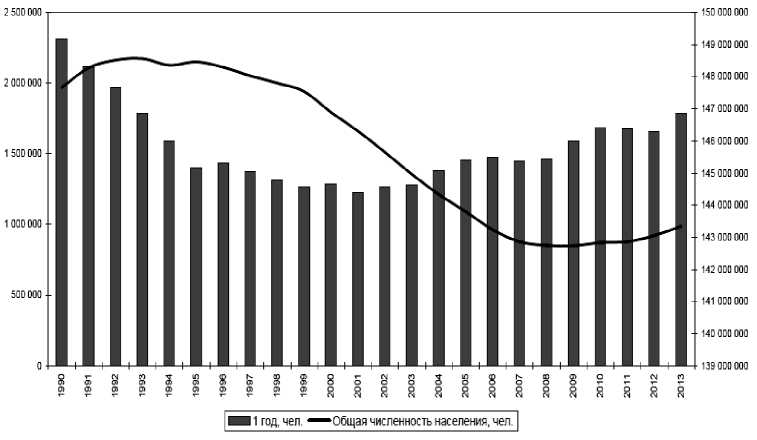
Рис. 3. Численность населения РФ на 1 января по категории «Рождение с учетом смертности в 1 год (1 год)», человек

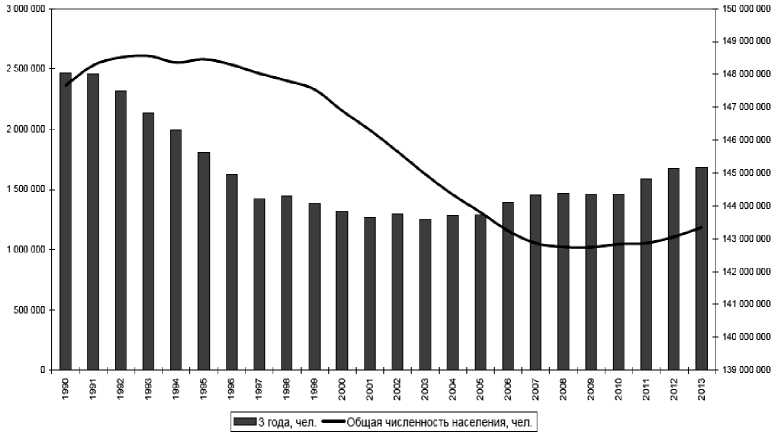
Рис. 4. Численность населения РФ на 1 января по категории «Дошкольный возраст (3 года)», человек

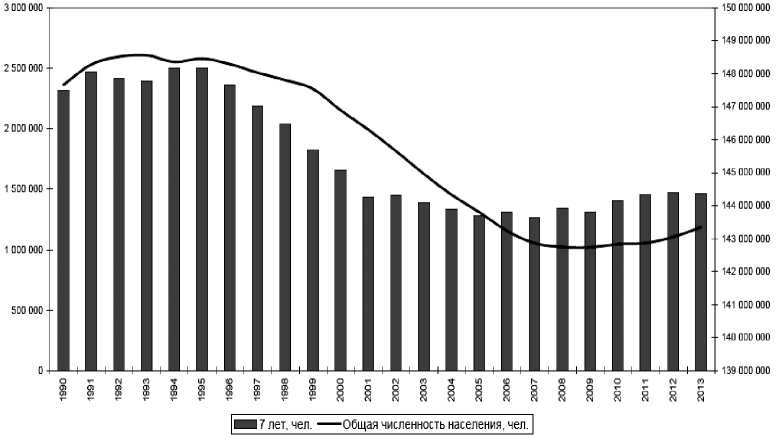
Рис. 5. Численность населения РФ на 1 января по категории «Начальная школа (7 лет)»,

человек

^е 16 лет, чел. —Общая численность населения, чел.

Рис. 6. Численность населения РФ на 1 января по категории «Старшие классы или СПО (16 лет)», человек

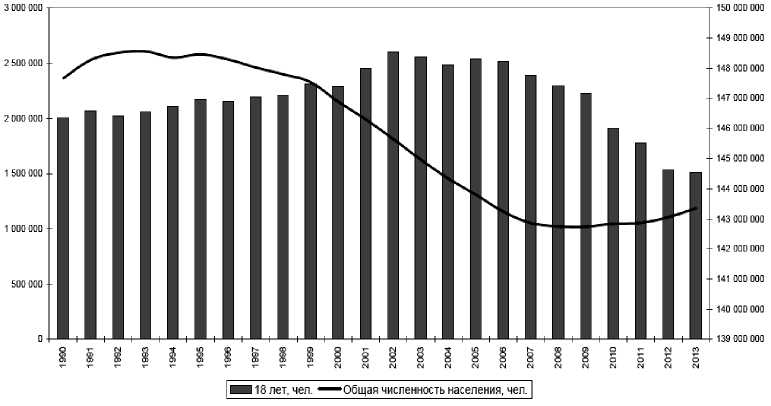
Рис. 7. Численность населения РФ на 1 января по категории «ВУЗ (18 лет)», человек

Систематическое снижение численности (см. рис. 7) с 2002 г. прекратилось и стабилизировалось в 201213 годы. Сейчас их количество составляет 1,5 млн. человек. Анализ всех представленных категорий стал основой формирования Гребневой модели.

Для наглядной демонстрации процесса формирования когортной выборки необходимо изучить период с 1990-2010 гг. (табл. 1).

Таблица 1

Когортная выборка данных РОССТАТа за период 1990-2010 гг., человек

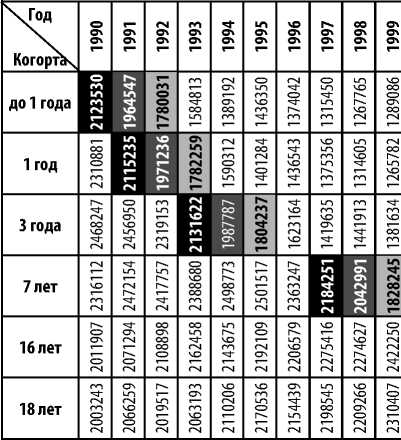
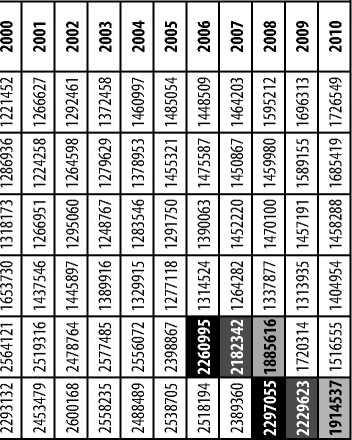
Источник: данные РОССТАТа и расчеты авторов

На приведенных в табл.1 данных отражен механизм формирования «волны», а также выбор когорты-гребня, позволяющей оценить показатели численности детей и молодежи на различных уровнях системы образования.

В рамках первого этапа исследования (параметризация модели) необходимо проанализировать показатели для периода с 1990 по 1995 гг. Данный диапазон позволит определить «полную» волну — гребень до 2013 года (табл. 2).

Таблица 2

Когортная выборка за период рождения 1990-1995 гг., человек

Год рождения Когорты/	1990	1991	1992	1993	1994	1995
Дети до 1 года	2123530	1964547	1780031	1584813	1389192	1436350
Рождение с учетом смертности в 1 год (1 год)	2115235	1971236	1782259	1590312	1401284	1436543
Сад (3 года)	2131622	1987787	1804237	1623164	1419635	1441913
Начальная школа (7 лет)	2184251	2042991	1828245	1653730	1437546	1445897
Старшие классы (16 лет)	2260995	2182342	1885616	1720314	1516555	1507135
ВУЗ (18 лет)	2297055	2229623	1914537	1777762	1662919	1555494

Источник: Расчеты авторов на основе данных РОССТАТа

В табл. 2 «волна» по всем выделенным возрастным категориям сгруппирована в один столбец. Визу- ализация когортной выборки за период детей, рожденных с 1990 по

1995 гг., приведена на рис. 8.

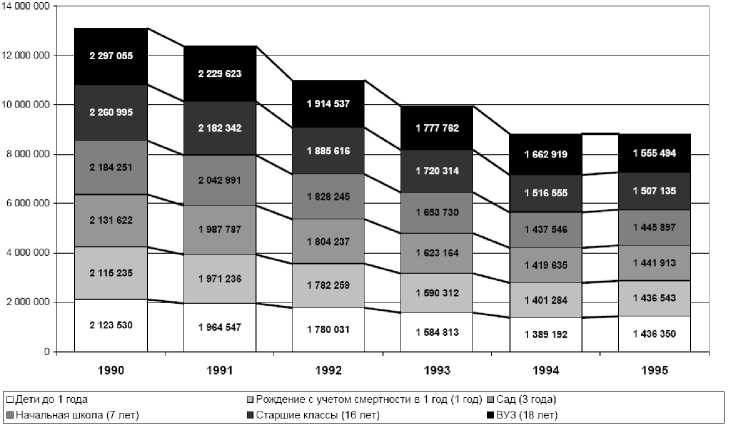
Рис. 8. Визуализация когортной выборки за период рожденных детей с 1990 по 1995 гг., человек

Из рис. 8видно, что имеется тенденция к уменьшению численности в каждой последующее когорте.

Для построения Гребневой модели были использованы методы эконометрического моделирования. Для этого осуществлена параметризация и определен вид зависимости на основе статистических данных. С помощью идентификации моделей и оценивании неизвестных параметров, выполнена верификация и осуществлен расчет возрастной структуры детей и молодежи на период с 2010-2031 гг. (рис. 9).

Согласно прогнозу количество учащихся в группе 16 и 18 лет будет постепенно расти.

Однако ситуация может измениться, если на следующем этапе моделирования будут учтены новые переменные. Более наглядно результаты моделирования можно представить в виде волновой диаграммы (рис. 10).

Таким образом, авторским коллективом разработанная Гребневая модель возрастной структуры детей и молодежи позволяет анализировать изменения демографических показателей с помощью эконометрического моделирования. С определенной долей вероятности (и учетом погрешностей в данных РОССТАТа) можно предопределять количество учащихся на различных уровнях образования. Использование Гребневой модели дает возможность планировать необходимое количество мест в дошкольных учебных заведениях, в школах, в системе СПО и ВПО, что в целом позволяет реализовывать стратегическое планирование и более эффективно управлять системой образования. С учетом изменения входных параметров данный подход может быть адаптирован для прогнозирования возрастной структуры учащихся в любом регионе: не только на макро-, но также на мезо- и микроуровне.

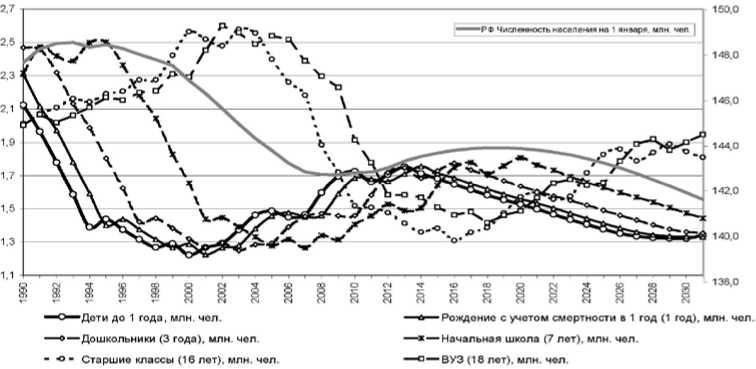
Рис. 9. Применение Гребневой модели для прогнозирования возрастной структуры учащихся (1990-2031 гг.), человек

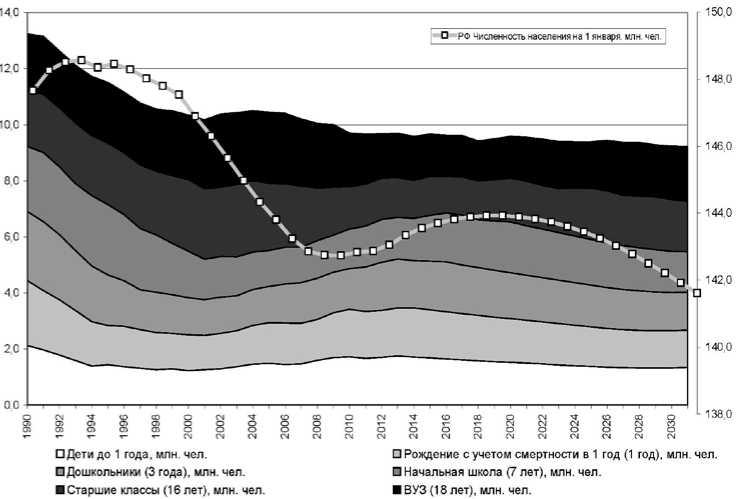
Рис. 10. Волновая диаграмма прогнозирования возрастной структуры учащихся на основе применения гребневой модели 1990-2031 гг., человек