H-spaces (H41,G) of type {41}: projective-group properties

A vector field X on a live-dimensional pseudo-Riemannian manifold (M, g) with a ， projective sti’ucture П is called an injlnite projective tr ( i-nsform ( i^ or a projective motion if the local 1-par am eter group of local transformations, which is generated by this field in a neighbourhood of each point т e M, consists of (local) projective transformations, that is, automorphisms of the projective struct иге П.

(Lxgij)，左=2仇/ 屮,k + 9注 R/ + gjk 夕,", where g is a function of t\ which we shall call a defining function of a projective motion X.

The equation (1) can be written in the form of two relations:

(the generalized Killing equation) and

九 ij,k = 2gijRk + gik 夕,j + gjkg,i

(the Eisenhart equation). If 夕 =const, that is, divX = const, then the vector field X preserves the affine connection and hence it is an infinitesimal affine transformation, or an affine motion.

An affine motion X is an infinitesimal homothety, or a homothetic motion when hij = const • gj and an infinitesimal isometry, or an isometric motion when hij = 0 [1].

After making a change of variables hij = @ij + 2 夕gij , where @ij is a symmetric bilinear form with the same Segre characteristic x (that is of the same type X)as hij. the equation (3) becomes

@ij,k = gik 屮 ,j + gjkg,i.                                             (4)

We call ,%j an h-metric of type x and we call (M, g) an h-space of type x [2].

Given the type of tensor hij, one can find solutions of the Eisenhart equation (3) and then of the Killing equation (2).

In a canonical skew-normal frame ( [3], p. 97) {匕} on V C M the equation ⑷ takes the form

九 ddpq +): 6%(Q%q®pR + Qp%®qR) = (^^夕)°p + (^^夕)0q , %:1

where Өһ is the canonical 1-form which is conjugate to %, ®pq = — ®qp is the connection 1-form, and pq,r = 1,..., 5.

In [4] h-spaces (%i,g) of type {41} were found, and necessary and sunicieut conditions for the existence of projective motion of type {41} were obtained. To calculate the maximal projective Lie algebra in (H41, g) it is necessary to obtain a general solution of the Eisenhart equation (3) in h-space ("4i,g). To solve this probleiiL one needs to study the inl.egral. ) ilil.y conditions (25) for the Eisenhart equation, which contain the curvature form Qij. In this case, spaces of constant curvature should be excluded, the structure of the projective group of which is well known [2].

The outline of the article is as follows. Basic definitions and formulas are given in Section 1. The curvature structure of the h-space ( 〃 4i ,g) is defined in Section 2. In Section 3 we derive the necessary and sufficient conditions that h-space (^41, g) be a space of constant curvature. In Section 4 we discuss the integrability conditions of the Eisenhart equation in (%i,g) and obtain an important characteristic of its solutions in an h-spасе (H41, g) of non-constant curvature. In Section 5 we establish necessary and sufficient conditions for the existence of a non-homothetic projective motion in h-sp а се (H41, g) of type {41}. and determine the struct uro of a non-homot het ic project ive Lie algebra in (% 1 ,」 ).

1. Computing curvature of (-H41, <7).

In the paper [4] a canonical skew-normal frame (匕)=(£jdj) has been defined with the following i components in the appropriate coordinates:

3            11

， 1      ，      (/ 2 — / 1 )^1/2, І     2(/ 2 — / 1 )³/²,

1            ³ £2            ¹ £1             5

3      8（ / 2 -力 ） 5 / 2 ' 3      2（ / 2 一力 ） 3 / 2 , 4      16（ / 2 -力 ） 7 / 2 '

『 =8（/ 2 - / і ）^1/2 （ （/ 2 -/ і ）² - :е" ） ' 『 =2（/ 2 - / і ）^1/2 （ Т 2 -Л - ^е* f= _A（/2 2 / 1 ） 1 / 2 ' 『= （/ i 「/ 2 ） ² '   5= ^3е （ ， ³ + 3 （， ⁴） ） + ^{1 - е}） ・

The canonical forms 电/ and 仇/ are given by the formulas

/ 0     0     0    6 1 / 1     0 \		/ 0   0   0   6 1    0 、
	0      0    6 1 / 1     6 1       0		0   0   6 1    0   0
Qpq =	0     6 1. / 1     6 1       0       0	' gpq =	0 6 1 000
	6 1. / 1 6 1   000		6 1 0000
	\ 0     0     0     0    6 2 / 2 丿		\ 0   0   0   0  6 2 丿

and the following equations are satisfied:

匕夕 ="д= 匕夕 =0'

d/ l = 2 （ 吗夕）仇 , 力 2 = 2（ 为夕 ） 。 5 ,

^ 13 =：（吗夕） 。 1 , 6^ 14 = - （吗夕） 0 2 , ^ 15 = "[ —,

²                                                   ./ 2 ^- ./ i

^ 24 =^{- （} 吗夕 ） 。 3 ' ^ 25 = " ”与 ）2 & + 广 A 仇,

（/2 -九）2     /2 -九 y5A           y5夕      1y5夕夕

“ ³⁴ =^- （吗冋" ⁴ ' “ ³⁵ =（ / 2-/y& ⁺ c^--/p ° ² + K-J &，

匕 9      招 9       匕 9      9 亠吗 9

3⁴⁵ = ČKF °¹ + 丁/戸 °² +       °³ + К-Л °⁴ +「 1 °⁵'

Here g=2/1 + 2 /2

⑸

⑹

⑺

⑻

⑼

（10）

is the defining function of a projective motion of type {41}⑴叮=%派°" is the 1-form of connection in the skew-normal frame （У^）, /1 = ет4 + （1 - е）к, /2 = /2（十5）, е takes values 0 and 1,呂 is a constant, 61'62 = ±1. [4]. Using the first Cartan structure equation d°〃 = — £5=1 £/®叮 A % and the formulas （9）, we find d°1 = -3^°1 A °2 -吿°1 A °5'

²                    ./2 ^- ./1

d°2 = -6 1 （吗 9）° 1 A ° 3 - 6² （ -? ° 1 A ° 5 - ⁶ ； ^（" ° 2 A ° 5 '

^{（ /} 2 一 力） ²          力 一 J1

d° 3 =	一屮 ° 1 A ° 4 -	6 2 （号 9 ） А （ / 2 - / 1 ） 3 ° 1 A °5-	62 （口 9 ） a 人 4 （ / 2 - / 1 ） 2 °2 A °5	第 5"° 3 A ° 5 , ./ 2 - ./ 1
d° 4 =	62 （ %3 ） A （/ 2 - / 1 ） 4 ° 1 A °5 -	62 （。 9 ） A （ / 2 - / 1 ） 3 ° 2 A °5	62 （ %3 ） a -（/ 2 -/I °3 A °5 -	小° 4 A ° 5 , ./ 2 - ./ 1
		d° 5 =-戸* ./ 2 - ./ 1	° 1 A ° 5 .

We introduce the notation

^A 1 三吗 д ， ^A 2 三 y5 屮，

0 1 三 ⁶ 1 ! 4 ^（I 4 夕 ） ，。 2 三 ⁶ 2 ^y 5 ^（y 5 夕 ） .

（11）

心 12 = 0' 心 13 = 0' d^ 14 = - 。 1 ° 1 A ° 2 + A ； 。 ] A ° 3 +   ~2 ° 1 A ° 5 '

^（/ 2 ^-九） ²

加 15

36 1 / 1 / 2

2(/ 2 - / 1 )

^ 1 Л 久 -

(/Ь ： - ( / 2 - / 1 )²) & ^Л 賑

心 23 = 0 ,

eiA2

d® 24 = — 。 1 仇 Л & +--2— ^ 1 Л & +

e ? A 1 A ? (/ 2 — / 1 )³

仇 Л % + 3 2 ¹ 出 Л & +

e 2 A 1 A 2 (/ 2 — / 1 )²

/   _  ^e 1 ^A 1 ^A 2 口 口 (    ° 2         ^2e 2 ^A 2 、口 口

²⁵ = ^- A-T^Л "^{3 -} ( U2-T1P - u2-/Р^Л "^5-

(/Т-Т Т - (І—І)²) 。 ^{2 Л} " ^5,

加 34 = - 。 1 仇 Л0 4 +

^e 1 ^A 1 ^A 2 2( / 2 — / 1 )³

0 1 Л0 2 +

e 1 A 1 A 2 2(/ 2 — / 1 )²

。 1 Л0 3

e 1 A 1 A 2 2(/ 2 — / 1 )

0 1 Л0 4 -

( Q      3e 2 ^A 2 、       」 Q      2e 2 ^A 2 、

I ( / 2 — / 1 )³   ( / 2 — / 1 )⁴ 丿&     ⁵   (( / 2 — / 1 )²   ( / 2 — / 1 )³ 丿仇 ⁵

(НТ! - (.j—l)2)。3 Л。5, did 45

e 1 A z A 1

^(/ 2 ^- / 1 )⁴

0 1 Л0 2 +

e 1 A 2 A 1 (/ 2 — / 1 )³

0 1 Л0 3 +

e 1 A 2 A 1 (/ 2 — / 1 )²

0 1 Л0 4 +

(    。 1          。 2     + ^4e 2 ^A 2         ^e 1 ^A 1

( / 2 — / 1 ) — ( / 2 — / 1 )^{4 +} ( / 2 — / 1 )⁵ — 2( / 2 — / 1 )²

。 2          ^3e 1 ^A 1

( / 2 — / 1 )^{3 +} 2( / 2 — / 1 )

3e 2 A 2 (/ 2 — / 1 )⁴

)

。 2 Л0 5 —

(J 一产之 )& Л 。 5 -( 乙一 ) 。 4 Л 。 5

^(/ 2 ^一力) ²    (. 7 2 ^一力 )³              / 2 ^-九   ^{( /} 2 ^一力) ² 丿

dA2 is similarly calculated.

Using the obtained relations and the second Cartan structure equation 。叮=心叮 + £ 5=1 e/i 皿 Л ®。 , we calculate the curvature 2-form 。叮 оf 九 -space of type {41}:

^e 2 ^A 2 ( / 2 — / 1 )²

0 1 Л 。 2 ,

Q 13

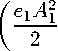
^e 2 ^A 2 ( / 2 — / 1 )³

)

0 1 Л0 2 —

^e 2 ^A 2 ( / 2 — / 1 )²

0 1 Л 。 3 ,

0 14 = — ( С 1 + Л 4 ) 。 1 Л 。 2 + (竺 一 ( е*з ) 。 1 Л 。 3 — (      2 & 人。 4 ,

(力^一九) ⁴/         \ ²     (力^一九) ³            (%^一九) ²

0 15 = - ( 7% -         ) 。 1 Л 。 5 , 0 23 = ( 竽- ) 。 1 Л 。 3 -

/ 2 ^-九(%^一力) ^{2                 2}     (%^一九尸丿

(J* 2 0 2 Л0 3 , 0 24 = - (a + ( J* 4 ) 0 1 Л0 3 + (婚 - ( e* з ) 0 1 人 0 4 +

(力 一 / 1 ) ²                            (力 一 / 1 ) ^{4                2}      (力 一 / 1 ) ³ /

（于 -     ）仆&-° 2 人 ％

2     （%^一九） 3 ，         （%^一九） ²

。 25 = - （J 汴 - 片也* ） 。 1 人。 5 - （ н 广 -       ） 。 2 人。 5 ,

（力 ^一 ） 1 ） 2    （力 ^一 ） 1 ） 3               力 ^一 ） 1    （力 ^一 ） 1 ） 2 /

出 4 = — ( C i +(      ) & 人 ％ + (竽-)奥人 ％—       賜人&,

⁽⁾ 2 ^-九产                ^{2     ()} 2 ^-九) 3 /           ⁽⁾ 2 ^-九) 2

о       (    ^C 2     I   ^е 1 ^ 1       3e 2 ^ 2 、@ м

°³⁵ = ^{- +} 2(K-A) - 「) 7 丿& 人 “ ^{5 -}

(- 户 ²" ) 。 2 人 。 5 - ( 产戸 -戸 2 下 ) 。 3 人 。 5 ,

^{( )} 2 ^-九) 2    ^{( )} 2 ^-力尸/          1 力^{- )}1   ^{( )} 2 ^-九) 2 丿

(    ^C 1 ^C 2         4e 2 — 2 e 1 — 1    、

⁴⁵= ((. ) 2 -. ) 1 )    ( ) 2 - ) 1 ) 4 ⁺ (. ) 2 -.) 1 )⁵    2( ) 2 - ) 1 )² 丿" ⁵

(    ^C 2        6 途 1 3 e2—2 、 л _Л л _

I ( ) 2 - ) 1 ) 3 ⁺ 2( ) 2 - ) 1 )   ( ) 2 - ) 1 ) 4 丿 ^{2    5}

( - П2^¥) 人 ° 5 - ( - ) 人

• ⁽⁾ 2 ^- ) 1 ) 2     ⁽⁾ 2 ^- ) 1 ) 3                  / 2 ^- / 1     ⁽⁾ 2 ^- ) 1 )2 /

2. H-spaces (-H41, g) of constant curvature.

Theorem 1. The necessary and sufficient condition for an h-space (" 41 ,9) 。/ 力 ype { 41 }力。 be a space

of constant curvature K: Qij = KOi Л Oj, is K1312 = 0, which is equivalent 力。 eiA2      62^42 О 三- “ 2 2、з = 0,                                (13) 2      ()2 - )1)3 moreover, Kij^i = 0, p^ = 0 for all (，/) and (k/) = (，/), th at is Q^j = 0, and any h-space "41 0/ type {41} of constant curvatiire. is flat.

Proof. We write the curvature 2-form as

Qij 三 £ Kij*i Ө_к 人仇(儿 / = 1,..., 5, k < /)                           (14)

(kl) and put Kijij = pij, then the formula (14) takes the form

Qij = PijӨі 人 Oj + £ Kijk/k Л Өі ( ， J k, / = 1,..., 5, ， < J, k < /),

(kl) = (ij) where, by virtue of (12), P12 = —-242   — .                      с -   ()    / )2 = p13 = p14 = p23 = p24 = Р34,                        (丄5丿 C2       -242 P15 =   £    £丨/£    £、2 = p25 = p35 = p45, 力一)1    ()2 - )1)2 and among the coefficients Kijki for (k/) = (，J) are nonzero only

K 1312 =

- 1 4 1      - 2 4 2    г         о      - 2 42 2      () 2 - ) 1 ) 3 ,   1412 =  C1   () 2 - ) 1 ) 4 ,

K l413 = K l312 =k 2313 ,K 2413 =k 1412 , k 2414 =k 1312 =k 2423 ,

k 2515

Q ,   262 老

(力一力) ^{2 +} (/ 2 - / l ) 3 ^{，    3414} =   ¹⁴¹ 2 ^，

。 2         £ l 用        36 2 ^ 2

( / 2 — / 1 ) 3 - 2( / 2 — / 1 ) + (力 — / i )⁴ ,

К 3525 = К 2515 , К 4525 = К 3515 , К 4535 = К 2515 ,

К 4515 =

° 1          ° 2          6 1 A 2         46 2 A 2 -/ 2 -/ 1     (/ 2 -/ 1 )4    2(/ 2 - / 1 )2  1  (/ 2 -/ 1 ) 5 ,

Equating К^ 恥 with (k,/) = (i,j ), i, j,k,L = 1,..., 5, to zero, we get the following five conditions:

6 1 用 6 2 ^ 2

2      (/ 2 - / 1 )³

- °^{1 -} (/ 2 - i)⁴ =^0,

- (/ 2 °²/ 1 ) ² + (/ 2 i /² ) ³ = ^0,

° 2         ⁶ 1 揚       3⁶ 2 A2  _ °

- (/ 2 — / 1 ) ³ - 2(/ 2 -/ 1 ) ⁺ (/ 2 — /I⁴ =

° 1          ° 2          61A2        46 2 A 2

/ 2 -/ 1 - (/ 2 — / 1 ) ⁴ - 2(/ 2 — / 1 ) ^{2 +} (/ 2 — /О⁵

Given the formulas (10), (11) and (5), the equation (17) becomes

46 1 f²6 2 (/ 2 ) 2 (/ 2 - / 1 ) A² - 2(/ 2 - / 1 ) 7

where /2 = с/?/"/⁵. Differentiating it with respect to t ³ , we find £ = 0, after that from (13) we get /2 = 0, it follows A1 = A2 = 0, °1 三 61y4(A1) = 0, °2 三 62y5(A2) = 0. In this case, the conditions (17)(21) are carried out identically, moreover, p 叮 三 0 for all i, j = 1, ...5. He nee, 0 叮 = 0 for all i, j = 1, ...5, therefore К = 0, and 九 -space (" 41 ,9) is Hat. Q.E.D.

3. Integrability conditions of the Eisenhart equation.

Theorem 2. Any solution (k,g,“) of the Eisenhart equation

▽k(Y, Z,爪)=2g(У, Z)爪少 + g(W, Z)У^ + д(У,爪)Z“, which is equivalent after change k = b + 2^g 力。the equation

▽ b(y, Z, 爪 )=g(W, Z)У^ + 9(У, 爪 )Z",

in. 九- spe ice. (%] ,g) of type { 41 } of /101 i-coi ?,s 力 ai z 力 c 〃广"〃力 ure satisjles the coi z diti01 z

3 = C 1

(2/1+2/2)

+ CO 〃 S 力 =C1^ + co 〃 s 力,

where the function g is defined by the relation (10), and q is an arbitrary constant.

P г о o f. In view of the invariance of the quantities 力 and the tensor nature of the equality (23), it suffices to prove it in the canonical skew-frame (5), where the equation (22) takes the form

而 pq + £ ⁶% ('q3pX + %% 3 成) = (% ³ )% + (鬲 ³ ) %,                (24)

九 =1

here ®р 刃 is defined by the formulas (9), and b_pq are the comp onents of the tensor b in the skew-frame

By differentiating the Eisenhart equation (24), we obtain its integrability conditions:

^bp%Q"q + MqQ"p = ^ph^^h A % + ^hq 。 " △ %

where Q^hp = £ 九。刃 p ， 3Ph 三 — %%3 — )'phH3 = ^hp- By equating the coefficients for identical basic 2-forms 19a A 0© left and right in (25), for (pq) = (13) and ( q/3 ) = (24) we find

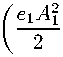
62^2

(/2 — /1)³

)bii

If bii = 0, then it follows (13), and, by Theorem 1, (%i,g) is a space of constant curvature. As this contradicts the assumption, we have bii = 0. We similarly get bi2 = bi3 = bi5 = b22 = b25 = Ьз4 = Ьз5 = b《4 = b《5 = 0.

From the equation (24), where ^hs are defined by the formu las (9), (10) and (5), for (pq) (11), (12), (33), (34) and (35), using the equalities (26) and considering that ^⁴ = 0, £⁵ = 0, we find

产& 3 = 0, 产& 3 + Юз = 0, 产 di3 + Юз + €³дз3 = 0, i               2           2               3           3           3

КЬзз = 0, = 1,..., 5),

@43 = 2ei Ьзз/1 , дб3 = 2 61Ьзз/2 .

From the equation (27) we derive 3 = 3(^x4,^x5) by using the formulas (5). Then from the equation (2$) it lollows Ьзз = eici = const. By rntegratmg the equations (29,) and (3U[ we obtarn

3 = ci

(^2/i+ 力

+ const = Ci^ + const.

Q.E.D.

4. Main theorems.

Theorem 3. Any covariantly constant symmetric tensor b 叮 in h-space (H4i,g) 。/ type { 41 } 。/ nonconstant curvature is proportional to the metric tensor:

b ， 3 = C2 92/     (C2 = const).

Proof. In the skew-normal frame (5) the equation b ,,,左 =0 takes the form

"bpq + ^3 eh (bhq^ph + bph^qh) = °. h=i

The integrability conditions for the equations (31) are obtained from (25) for 3 = const and have the form bphQ) + bhq Q' = 0.

Hence, as in the previous case, we obtain the equalities (26) in h-space (%i,g) of non-constant curvature. From (32) for (pq) = (14), (33) it follows Ob?4 = ОЬзз = 0, and since in h-space (^4i, 9) of non-constant curvature D = 0, then b?4 = Ьзз = 0. From (31) for (pq) = (14), (23), (55) we find dbi4 = 0, 曲 23 = 0 and "655 = 0, whence il. lollows that bi4, 623 and 655 are constant.

From (32) for (困) =(13) we find

。(仇4 - b23)= 0, from here for 0 = 0 we have 仇4 = 623, after that from (31) for (pq) = (45) we derive

(實矶 - £і ⁶ 14 ) А2 = ^0,

( £2^55 - £1 ⁶ 14 ) Ai = 0.

If (£2655 — ei&i4 ) = 0 then Ai = Л2 = 0; this implies (13) and by Theorem 1 ("41,9) has constant curvature, which contradicts the assumption. Therefore, £1614 = £1623 = £2 655. Putting 614 = eiC2 we find finally 6Pq = c2g_p ① where (g_pq ) is defined by (6). Q.E.D.

Since the vector field X is an affine motion in ("41,9), if and only if (Lx g),“ = 0, then the theorem (3) implies

Theorem 4. Every affine motion X in an h-space ("41, g) 。/ 力 ype { 41 } 。/ non-constant curvature is an infinitesimal homothety: Lxg = cg, c = const .

Since any two solutions Һ1 and Һ2 of the Eisenhart equation (3) with the same right-hand side can differ only by the covariantly constant tensor 6, from the theorem 2 and the linearity of the equation ⑶ it follows that the general solution of the Eisenhart equation in an h-space ("41, g) of non-constant curvature can be written in the form qh + 6 or, by virtue of the theorem 3, in the form qh + C2g, where h = q + 2gg, g and q are defined in the skew-normal frame (5) by canonical forms (6) [4], q, C2 are constant. From here it follows

Theorem 5. A vector field X is a projective motion in an h-space ("41, g) of non-constant curvature if and only if

Lxg = C1h + c2g 三 q(q + 2夕g) + C2g, where 夕 is the defining function of the projective motion X, g and q are defined in the skew-normal frame (5) by canonical forms (6), C1, C2 are arbitrary constants.

• Theorem 5 implies

Theorem 6. If an h-spa ce ("41, g) 。/ type {41} 。/ non-constant c urvature admits a r-dimensional non-homothetic projective Lie algebra 4, then this alge bra contains a (r — 1)-dimensional homothetic subalgebra.

Proof. If (X1,..., X,) is the basis of the Lie algebra 4, then Lx_s g = c ]h + c 2g, s = 1,...,r, where one of the constants c 1, for ex ample, c 1 is nonzero (otherwise P_r consists of homotheties). In the s                        1

new basis Z1 = X1, Z 『 = c ]X 『 —c 1X1 we have Lz 『 g = (c 1 c2 — c2 c 1 )g, 丁 = 2,...,r. Q.E.D.

1           T                         T '       1T 1 T