How to explain the efficiency of triangular and trapezoid membership functions in applications to design

For engineering design, expert knowledge is often important . In many engineering design problems, it is often very important to take into account the opinion of the human experts.

Expert knowledge is not easy to take into account. Taking into account expert’s knowledge is not always easy, since experts often formulate their knowledge not in precise computer-understandable terms, but by using imprecise (fuzzy) words from natural language such as “small”, “approximately”, “close”, etc. To take imprecise expert knowledge into account, Lotfi Zadeh came up with special fuzzy techniques [1-6].

1    First stage of fuzzy methodology: eliciting membership functions.

In the fuzzy approach, first, we describe the meaning of the corresponding natural-language words in precise numerical terms. For this purpose, for each such word (e.g., for the word “small”):

• ■    We provide the expert with several possible values x of the corresponding quantity,

• ■    For each of these values, we ask the expert to mark a point, on a scale from 0 to 1, to what extent the given value satisfies this property (e.g., to what extent this value is small).

The resulting points ц _P(%) £ [0,1] corresponding to different values x form what is called a membership function or a fuzzy set describing the corresponding natural-language property P .

2    Second stage of fuzzy methodology: combining membership degrees

An additional problem stems from the fact that many expert rules have several conditions: e.g., “if the road will have heavy traffic and the region experiences drastic changes from freezing to thawing, then the road pavement must be made reasonably resilient to such changes.” The condition to this rule contains two imprecise natural-language words: “heavy” and “drastic”. In the ideal world,

• ■    In addition to asking the experts for all possible values of ц_пeaV(( t) and ц_{dr asttc}(c),

• ■    we should also ask, for all possible combinations of traffic t and temperature change c, to what extent the above condition is satisfied for the corresponding pair (t, c).

However, in practice, already asking the expert about all possible values of one quantity takes a long time. So, asking the expert about all possible pairs is not realistically possible.

Since we cannot elicit, from the expert, the degree to which each pair satisfies the corresponding condition, we must therefore estimate this degree based on what we know, i.e., on the degrees to which the traffic is heavy and to which the temperature change is drastic. In general, we know the degrees and to which imprecise statements and are true, and based on these degrees, we need to estimate the degree to which the “and”-combination & is true. Let us denote the corresponding estimate by / & ( a, b ).

The algorithm that computes these estimates based on the two given degrees is known as an “and”-operation or a t-norm. The t-norm has to satisfy several reasonable properties. For example, since A &  В means the same as В & A , we expect that the estimates for these two “and”-combinations should be the same, i.e., that f & (a, b ) = f & (b , a) for all a and b.

Similarly, since A & (В &  C) and (A &  В ) &  C mean the same, we expect that the resulting estimates are equal, i.e., that f & (a, f & (b , c)) = / & (/ & (a, b ), c) for all a, b, and c.

All t-norms that satisfy all these properties are known. The most widely used “and”-operations are f&(a, b ) = min(a, b ) and f&(a, b ) = a • b, but many other operations are also used.

3    Triangular and trapezoid membership functions are usually very efficient

In principle, if we ask an expert, we can get different shapes of membership functions. In the beginning, practitioners tried to describe these membership functions as accurately as possible. However, it soon turned out that in most applications, it is sufficient to consider simple membership functions whose graphs have triangular or trapezoid shape (See Figure 1).

To be more precise, triangular membership functions are the following functions which are different from 0 on an interval [x,x] with midpoint x:

• ■    they linearly increase from 0 to 1 when x is smaller than the midpoint x and then

• ■    they linearly decrease from 1 to 0 when x is larger than the midpoint x.

• ■    In precise terms:

• •    ц(x) = ^X—= when x <  x <  x x - X      —

• •    ц(x) = =—^X when x <  x <  x

X - x

• •    ц(x) = 0 when x <  x and or when x >  x.

Trapezoid membership functions also have an interval in the middle when the function is identically equa l to 1. To be more precise, we select four values x <  t <  t < and then we take:

• ■   jw(x) = 0 when x <  x

• ■   ц(х) = ^ _ ^ when x <  x <  t

• ■   jw(x) = 1 when t <  x <  t

• ■   jw(x) = ^ _ ^ when t <  x <  x

• ■   jw(x) = 0 when x >  x

Open problem: why are these membership functions efficient? While empirical evidence shows that triangular and trapezoid membership functions are efficient in many engineering applications, there is still no convincing general explanation for this empirical efficiency.

A partial explanation was provided in [7], but this explanation is only valid when we use a minimum t-norm. In this paper, we show that a similar explanation can be made general by extending it to general “and”-operations.

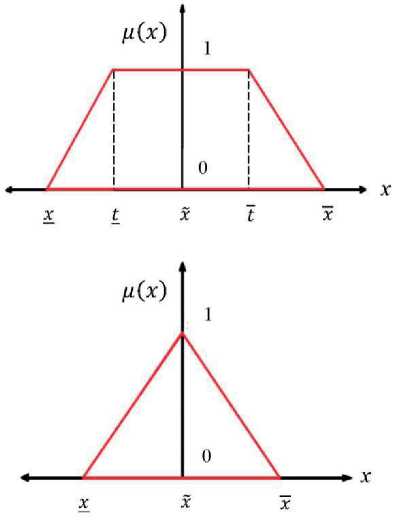
Figure1 - Graphs of membership functions have triangular or trapezoid shape

4 Main idea behind known partial explanation: a brief reminder

To explain this main idea, let us recall, in some detail how membership functions are usually elicited.

Elicitation of membership functions: first step . Usually, for each property, there is a threshold below which, according to the expert, the corresponding property is definitely not satisfied. For example, experts may have different opinions on what constitutes warm, but for every expert, there is a temperature below which it is clearly not warm. For some people from the North, this threshold may be 14 C, for people from the tropics, even 19 C may be chilly, so for them it will be around 22 C, but there is such threshold for every expert.

In precise terms, this means that /z(%) = 0 when x <  x.

Elicitation of membership functions: second step . Similarly, there exists a threshold above which the corresponding property is definitely not satisfied. This means that [л(х) = 0 when x >

.

Elicitation of membership functions: third step. There also usually exist values for which the corresponding property is definitely satisfied. For example, for “warm”, most people will agree that 25 C is warm.

Sometimes, there is a single value ̃ for which the original property is definitely satisfied. Sometimes, there is a whole interval of values [t, t] for all of which the given property is definitely satisfied. For all such values x, we have [л(х) = 1.

Elicitation of membership functions: fourth step . For the intervals [ x, x] and [ x,x] (or, alternatively, [x, t] and, [t ,x]), the membership degrees change from 0 to 1 and then from 1 to 0. These are the values that we need to elicit from the expert.

For each of the intervals, to elicit these values, we provide the expert with several values x0 < xT < x2 < ••• < __ _ !

< x

n

from the corresponding interval - where and are the interval's endpoints - and elicit the corresponding membership degrees ц_t = ц(x_i') for i = 1, .„,x_n (the values ц₀ and ц_п corresponding to endpoints are known). Usually, the values x^ are equally spaced: х_г — x ₀ = x₂ — x ₁ = •-, so that ц i = Ц₀ + i " h, where we denoted h = x₁ — x ₀.

Main idea behind the known (partial) explanation of the effectiveness of triangular and trapezoid membership functions. When the value x ' is close to the value x (x ' « x), we do not expect that the expert's degree of confidence ц(x ' ) that x ' satisfies the given property to be much different from the expert's degree of confidence ц(x) that the original value x satisfies this property: we should have ц(x) « ц(x ' ). For example: if x is reasonably small, and x ' is close to x, then it is reasonable to conclude that should also be reasonably small - with almost the same degree of smallness as .

In other words, if x and x ' are close, then the values ц(x) and ц(x ' ) should also be close. For large , the differences between and are small, so is close to . Thus, we conclude that for every , the values and should be close.

The more this property is satisfied, the more it is reasonable that the values adequately describe the expert's knowledge. It thus makes sense to select the values that satisfy the above property to the largest possible degree. In precise terms: for each possible sequence of the values , we can find the degree to which the above property is satisfied, and then as the most adequate description of the expert's knowledge, we select the values for which this degree is the largest possible.

How can we describe this degree? What does it mean that two values and are close? Intuitively, it means that the absolute value of their difference |ц_t — ц _ ₁| is small. Let s(v) denote the membership function corresponding to “small”. Then, for each the degree to which and are close is equal to 5(|ц_t — ц_t _ ₁|), and the degree to which this closeness condition is satisfied for i = 1 and for i = 2, etc., is equal to

• ⁽¹⁾                     / & (5^(|Ц i — Ц о |),5⁽|ц 2 — Ц 1 ^|),^,5^(|ц _п — ц_п _ J))

for an appropriate “and”-operation / & ( a, b ).

We must find the values ц₁, .„,ц_п _ i for which the expression (1) attains the largest possible value.

5 Analysis of the problem and the resulting justification

It is reasonable to expect that this optimization problem has a unique solution . In engineering problems, in principle, we may have optimality criteria that allow many different solutions. For the same problem, we have several solutions which are equally good according to the selected criterion. However, from the practical viewpoint, this means that the corresponding criterion is not final.

For example, if we have several plane designs with similar energy consumption and similar manufacturing and exploitation costs, this means that we can select, among these designs, the one with the smallest negative effect on the environment - and thus narrow down the set of all optimal designs. Eventually, we will end up with a final optimality criterion for which exactly one alternative is optimal. From this viewpoint, it is reasonable to require that our criterion (1) is, in this sense, final - i.e., that it leads to the unique selection of the corresponding membership degrees ц < .

Let us describe this requirement in precise terms.

Definition 1

• ■    By a membership function , we will (as usual) mean a mapping s (v ) from real numbers to the interval [0,1] .

• ■    By an n- aggregation operation , we mean a function /(a₁, ^, a_n) of n variables a _t E [0,1] with

values from [0,1] which is symmetric, i.e., for which:

f (^a 1 , -■, ^a n ) = ^{f( a} tt( 1) , ■■■, ^a n-(n) )

for all and for any permutation .

• ■    We say that a pair (f & , s,, where f & is an n-aggregation operation and s is a membership function, is final for increasing sequences if there exists exactly one sequence of values щ₀ = 0 <  p.1 < щ 2 < '" < M_n = 1 for which the expression (1) attains its largest possible value. The corresponding sequence will be called the optimal increasing sequence.

Proposition 1

For every pair ( f & , s) which is final for increasing sequences, the optimal increasing sequence has the form щ = A

Comments

• ■     For reader's convenience, the proof is given in the special (last) Proofs section.

• ■    According to this result, for the optimal increasing section of the membership function, we have щ (x_z) = ц(х₀ + i • h) = щ = к Let us describe щ (x_z) in terms of X[.

From x_t = x₀ + i • h ,we conclude that i = ^{x 1} ^^x0 , thus ц.(х^ = ^x^ ^x° , i.e., ц(х^ = a • X_t + b where a = ^ and b = — ~^. So, the optimal membership function ^(x) on the interval [x, X] is a linear function that takes the value 0 for x = x, and the value 1 for x = X, thus, ц(х) = |—| . This is exactly the increasing linear segment that we have been trying to explain.

• ■    Proposition 1 does not require that the n -aggregation operation is minimum - it can be any t-norm. Moreover, we do not even require that this operation be a t-norm: we do not require its associativity or monotonicity. So, our result is even more general than what we wanted.

• ■    A similar result holds for optimal decreasing sequences.

Definition 2

We say that a pair ( f & , s,, where f & is an n-aggregation operation and s is a membership function, is final for decreasing sequences if there exists exactly one sequence of values щ₀ = 1> щ₁> p ₂ >  •- > щ_п = 0 for which the expression (1) attains its largest possible value. The corresponding sequence will be called the optimal decreasing sequence .

Proposition 2

For every pair ( f & , s) , which is final for decreasing sequences, the optimal decreasing sequence has the form щ = 1 — ^ .

Comment

According to this result, for the optimal decreasing section of the membership function, we have ц(х^ = щ (x₀ + i • h) = щ = 1 — к Let us describe щ (x_z) in terms of x_t. From x_t = x₀ + i • h, we have i = ^{x 1 x 0} , thus ц.(х^ = 1 — T—T” i.e., M(x_t) = a • x_t + b , where a = — ^ and b = 1 + ^

So, the optimal decreasing membership function щ(х) on the interval [X,X], is a linear function that takes the value 1 for x = X, and the value 0 for x = X, thus, щ(х) = |—| . This is exactly the decreasing linear segment that we have been trying to explain.

6 Proof of Propositions 1 and 2

It is sufficient to prove Proposition 1, the proof of Proposition 2 is similar.

Let us prove, by contradiction, that for the optimal increasing sequence щ_t, we have щ — щ₀ = M₂ — M ₁ = '", i.e., that all the differences Д< = щ — щ_t__г are equal to each other.

Indeed, assume that some of these differences are different, i.e., ∆ ≠∆ for some ′ and ′′. Without losing generality, we can assume that i‘ <  i ‘‘. In this case, we can form the following auxiliary sequence .

• ■    for i <  i ‘, we take щ ■ = щ _t;

• ■    for i = i ' , we take / / = H i '__г + Д_t ', ;

• ■    when i ' <  i <  i '', we take h ■ = H i + (Д^'' — Д _t , );

• ■    finally, for i >  i" , we again take h ■ = h . .

This sequence is different from the original sequence , since ∆ ≠ ∆ and thus, Hi, = H i ' _ i + Д ' ^ H i, = Hi I _ ! + ^Д i = H i..

On the other hand, the differences ∆ ≝   - corresponding to the new sequence has the following form:

• ■    for i < i', we have Д ■ = Д _i,

• ■    for ', we have Д Д ;

• ■    when          '', we get Д Д ;

• ■    for i = i'', we get Д ■ / = Д ■ /, ; and

• ■    for i > i'', we again get Д ■ = Д_i.

Thus, the new sequence of differences ∆ is obtained from the original sequence of differences ∆ by an appropriate permutation π: namely, by a permutation that swaps the indices ′ and ′′ and leaves all the other indices unchanged. Thus, the values з(Д ■ ) = s(| /1 - h' i _ J) are also obtained from the values з(Д_i) = s(|h _i — h _i _ _i |) by a similar permutation.

Since we assumed that the n-aggregation operation is symmetric, i.e., that the result of applying this operation does not change if we simply permute the inputs, we thus conclude that

• (2)             / & (s^(|H i - H 0D ,s^(|H 2 -H 1 |), -,s^(|H П - н П_ iD)

= f & (s^(|H i - H o ^|),s^(|H 2 - H i ^|),^,s^(|H n - H n_ iD)

• i .e., that the expression (1) attains the same value for both sequences and .

Since we assumed that the sequence is optimal, this means that for this sequence, the value of the expression (1) is the largest possible. Thus, the above equality (2) shows that the value of the expression (1) for the new sequence h' _i is also optimal. So, we have two different sequences h _i and ′ on which the expression (1) attains its maximum – which contradicts to our assumption that the pair (/ & , s) is final for increasing sequences.

This contradiction shows that the differences ∆ cannot be different, so they are all equal: Д i = Д 2 = - = Д п , i.e., H i - H o = H 2 - H i = ^ = Д 1

Thus:

• ■    From h 0 = 0, we conclude that h 1 = Д 1 .

• ■    From h ₂ - H_i = Д 1 , we conclude that h ₂ = H_i + Д 1 = 2Д 1 .

• ■    By induction, once we have shown that h _i = i • Д 1 , we can conclude that

H_i + 1 = H_i + i • Д 1 + Д 1 and thus, that h _i + 1 = (i + 1) • Д 1 .

• ■    So, we conclude that h _i = i • Д 1 for all i.

• ■    In particular, for i = n, we conclude that H_n = ^ • Д_г, hence Д_t = - and thus,

^H i = i-A i = n

The proposition is proven.

Acknowledgments

This work was supported in part by US National Science Foundation grant HRD-1242122 (Cyber-ShARE Center).

The authors are thankful to Professor N. Borgest for his encouragement and valuable discussions.