Hyperbolic-logarithmic model of nonlinear electrodynamics

It is well known that strong electromagnetic field has strong connection with nonlinear theory. QED one-loop quantum corrections give a non-linear terms in classical Maxwell's Lagrangian [1]. Nonlinear electrodynamics uses in a wide range of contexts :cosmology and astrophysics [2], high power laser technologies and plasma physics [3], nuclear physics [4].

On the other hand, some models of nonlinear electrodynamics can solve the problem of Coulomb singularity, namely infinite energy of a point-like charge, which comes out in Maxwell?s electrodynamics. The most famous example is Born-Infield electrodynamics [5]. In arcsin-electrodynamics [6] and generalized ModMax electrodynamics [7] this singularity is also absent.

Considerated model contains finite energy of a point-like charge as well. This fact makes Hyperbolic-logarithmic model more attractive for deep investigation.

We use the Heaviside-Lorentz system with 方 =c = s = 〃 ° = 1, Latin letters run from 0 to 3.

1.    The model

In this paper we introduce a new model of nonlinear electrodynamics witch given by Lagrangian:

£ =-尸-]@"九(/3尸)--[ln(1 + 7尸)+ ln(1 - 8f)].(1.1)

Here 尸 =4 月左 F * =2(B² - E² ) - invariant of electromagnetic field, A,B - dimensionless parameters,

0 - parameter with dimension L4. First pair of Maxwell equations is following

Second pair of Maxwell equations, of course, remains unchanged:

&F* 注 =0 .

(1.3)

The electric displacement can be calculate with the help of expression D = d£ /dE:

D

厶 ^A -вс 尸 、 〔 1 - (" )² 丿

(1-4)

The magnetic field is given by H = -d£/dB:

H О в.

We can represented equations (1.4) and (1.5) in tensor form:

。 2 = G/ E^j ,   H, = 〃-・ 1 B^j ,

(1.5)

(1.6)

where gj and 〃/ - electric permittivity and inverse magnetic permeability tensors, respectively. We can write components of these tensors:

Gj = 〃 J = e6" ,  € = (] +

A - BC 尸 1 - (B 尸 )²

.

(1.7)

First pair of Maxwell's equation can be rewritten in the D - H framework:

dD

VD = 0,  — - Vx H = 0 .

(1-8)

Second pair of Maxwell?s equation has the standard form:

dB

VB = 0 ,   — + Vx E = 0 .

(1-9)

In order to see the dual symmetry of this model, from equations (1.4) - (1.6) we can obtain :

DH = /Е B = E B.

(1.10)

In other words, dual symmetry is broken [8] . In case (A = 0, C = 0 т e = 1 ) we arrive at classical electrodynamics with dual symmetry.

2.    Electrostatics

In this section we consider electrostatic case (B=H=0). Assume that a point-like charge q located al. r = 0. Equation for this charge is given by with the solution:

Taking into account (1.4), we obtain

E 。

▽ D о = qb(r)

D 0 = Л

47rr3

(1 +

A + ” ~^

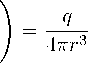
Solution of this equation at r т 0 is given by:

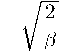
(2.1)

(2.2)

(2.3)

(2.4)

So, we can see what in this model maximum electric field is finite. Coulomb singularity is absent like in Born-Infeld theory.

3.    Energy-momentum tensor

In this section we find canonical and Belinfante energy-momentum tensors. The expression of canonical energy-momentum tensor is:

T 泳=- @A% ( F 嗚 + ^(A /税仆 ) -产£ .            (3.1)

This tensor is conserved &T 萌 =0 but is not symmetrical and gauge-invariant. So, we obtain symmetrical Belinfante tensor by the relation [9]:

where

and

T 駒)= T 派 + -X -,

X 皿 =1 (п%8* - n?s 唸- n*s 臨，)

п ^гк = —些— = ^гк

= д(& Ak )=      .

(3.2)

(з.з)

(3.4)

Obviously, X'2^k = — X 2^1k that give give rise to Сд^X'2^k = 0. So, using (3.1)-(3.4) we can obtain:

T 淸)= —F 皿 ( ғ% + ^{( A} J 芸戸 )—产乙             ( 3.5)

The trace of Belinfante tensor is

Tk = — 4 ( ]_.尸 ) 2 ) — 丁 th(!3 尸 )+ 豆 [ln(1+ " ) + ln(1 — / 尸 )].        (3.6)

If A = 0 and C = 0 we arrive at Maxwell electrodynamics. The trace of energy-momentum tensor (3.6) becomes zero.

4.    Energy of the point-like charge

In this section we study the electric energy of point-like particle - electron. In electrostatic case (B=0) the energy density is given by:

in ( 1 + 于) +ln ( 1- 于 /HD

尸 ₀₀     2 1 A +         A     //E² 、    C

P = ' ( В ) = ^E (j+ 「 T 丿^- §a 『 c"( 亍)+〃

Total energy can be obtain from: £ = f p^dV. Using new variables [6]

X

4 ， 2 开 r² e 強

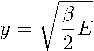
(4.2)

we can find expression for total energy:

"⁴ 2 二妥广遂卜( ¹ + 中产) ^-5/ ) + ^{C ln(1 -} / )]

(4.3)

Taking into account (2.3) we can write

1 -y4

7?=------------：.................... - y(1 - y4 + A + Cy2)

(4.4)

Thus, we can transform integral (4.3) to

/ 4 2

e2    /1 y²(1 — y² + 2(A + Cy²)) — Aarcth(y2)(1 — y⁴) + 与 (1 — y⁴) ln(1 — y⁴)

2¥ 西 J о                y⁽2)(1 — y⁴ — A + 2Cy²)² У1 — y⁴

X ( 4y⁴(1 — y⁴ + A + Cy²) + (1 — y⁴)(1 — 5y⁴ + 3Cy² + A) ) dy .               (丄 5)

With the help of numerical calculation of integral (4.5) we can realize the Abraham and Lorentz idea [10] about pure electromagnetic mass of electron. Let's consider the Heaviside-Lorentz system with

q = 72 = We obtain e = , 4 冗 q 仁 0 . 30286. 4 亓 137                      V

On the other hand, we can use quantities of classical electron radius r 。 = 2.818 fm and electron mass 0 , 511 、 I eV to obtain dimensionless left pari, of (4.5) ：炉 4 2 = 1 . 440 .

Numerical calculus gives that, for, example, this value corresponds to the following quantities of model parameters:

A = 0, 008 В = 0,0011.

(4-6)

Conclusion

We introduce a new, "Hyperbolic-logarithmic" model of nonlinear electrodynamics with three parameters: dimensionless A, В and dimensional /. After finding the field equations of the theory, we calculated the electric field of a point-like charge and we showed that at the origin - the location of the charge - it takes a finite value, that is E 。 = ^/2 , and is not singular. We showed that the dilatation symmetry is broken due to the nonzero quantities of parameters. We obtain the canonical and symmetric Belinfante energy-momentum tensors. Moreover, we show the example of values of model parameters, witch corresponds the idea about electromagnetic mass of electron.

Acknowledgments

The work was supported by the Russian Foundation for Basic Research (Grant N 20-52-05009).