Идентификация массовых распределений жировой фазы в молоке с помощью универсальных распределений Пирсона

Использование связи значений масс распределения жировых шариков по массовым или объемным фракциям [1, 2] со спектром времен релаксации молока от акустических свойств раствора [3] при параметрической идентификации представляет трудности по следующим причинам:

• -    число точек H ( т ) ограничено количеством их измерений;

• -    разная разрешающая способность по массе и частоте усложняет сопоставление точек, полученных экспериментально, на кривых релаксационного спектра и распределения масс жировых шариков по массовым или объемным фракциям с релаксационным спектром молока;

• -    вероятное увеличение случайной ошибки без фильтрации исходных данных.

То есть необходима аппроксимация экспериментальных значений H (τ) и распределения жировой фазы. Рассмотрим синтез аппроксимирующей зависимости на примере массового (объемного) распределения жировой фазы в молоке. Поскольку полная функция распределения начинается с нулевого значения и заканчивается нулевым значением, проходит через один или несколько максимумов и при этом вид спектра заранее неизвестен, то для его аппроксимации можно использовать решения дифференциального уравнения Пирсона [4, 5]:

dHT1) = А T + \ 2 • HT) , (1) ат b0 + b1T + b2т где a, b0, b1, b2, — постоянные.

Общее решение этого уравнения может быть представлено в виде:

j ( т + a ) d T

h ( t ) = He ^b ° ⁺ b ¹ ' ^{+ b} 2 ^{T 2}             (2)

Параметры a, b0, b1, b2, определяются по методу моментов:

a — м (м + 3ц2) / A, bо = - ^2 (4 ^2 M4 — 3^2) / A,

* b — - M ( ^ 4 + 3 M ) / A, b 2 — ^- ( ²M Ц 4 ^- 3 ^{M -} 6 M ₂ ) / A, A — 10 MM - 18 м - 12 М ,

где μ 1 , μ 2 , μ 3 , μ 4 – первые четыре центральных момента распределения измеряемой величины:

n

A k — X ( т - M ) k • H ( т ) ,            (4)

i — 1

где k – порядок рассматриваемого момента;

n – количество экспериментальных точек.

Структура решения дифференциального уравнения (1) зависит от полученных корней V ₁, ^ уравнения [5]:

b ₀ + b ₁ T + b 2 T ² — 0           (5)

Для проверки корней данного уравнения вводится параметр:

$ —

b i²

^{4 b} 0 ^b 2

Величина æ называется критерием Пирсона (каппа Пирсона) и ее значения определяют следующие свойства корней уравнения:

• -    Если $ <  0, уравнение (2) имеет действительные корни разных знаков.

• -    Если 0< $<1, уравнение (2) имеет комплексные корни.

• -    Если $>1, уравнение (2) имеет действительные корни одного знака.

Всем этим вариантам Пирсон ставит в соответствие три основных типа своих кривых, которые он назвал кривыми I, IV и VI типа. Также $ может принимать значения 0,1 ± », что дает переходные типы кривых. Всего семейство кривых Пирсона включает 12 типов, плюс нормальную кривую.

Имея рассчитанный параметр æ, можно определить вид кривой, аппроксимирующей экспериментальные данные.

В случае нескольких основных времен релаксации согласно принципу суперпозиции релаксационных процессов в молоке суммарная функция f ( T , ^ ) будет аппроксимироваться взвешенной суммой функций плотности в двумерном виде:

N f (T ,^) —X 5f (T ,^),      (7)

I — 1

где i – номер рассматриваемого релаксационного процесса, N – количество рассматриваемых релаксационных процессов, ^ - весовой коэффициент для i -го релаксационного процесса в общие механические потери.

Таким образом, алгоритм, с помощью которого осуществляется построение математической модели, которая описывает спектр времен релаксации в молоке, будет выглядеть следующим образом (рисунок 1):

• 1.    Разделение множества всех экспериментально точек в плоскости ( T , ю ) на под-

• множества, соответствующие отдельным выборкам и относящиеся к конкретному релаксационному механизму.

• 2.    Создание из множества экспериментальных точек, соответствующих каждому механизму релаксации, подмножеств экспериментальных точек, связанных с фиксированным частотам или температурам, для создания выборок условных распределений по частотам и температурам.

• 3.    Приведение к нормированным значениям для расчета выборочных моментов условных распределений.

• 4.    Расчет выборочных моментов M _m , M T условных распределений.

• 5.    Расчет коэффициентов квадратного уравнения в знаменателе (1) С _ю, С и вычис

• 6.    Выбор типа распределения из семейства универсальных распределений Пирсона.

• 7.    Расчет параметров распределения Г ^ Г т , п_ю , ^п т .

• 8.    Дополнительное уточнение коэффициентов суммарного многомодального распределения с помощью метода покоординатного спуска по среднеквадратичному критерию и начальными приближениями, полученными на этапе 7.

• 9.    Оценка адекватности и точности модели.

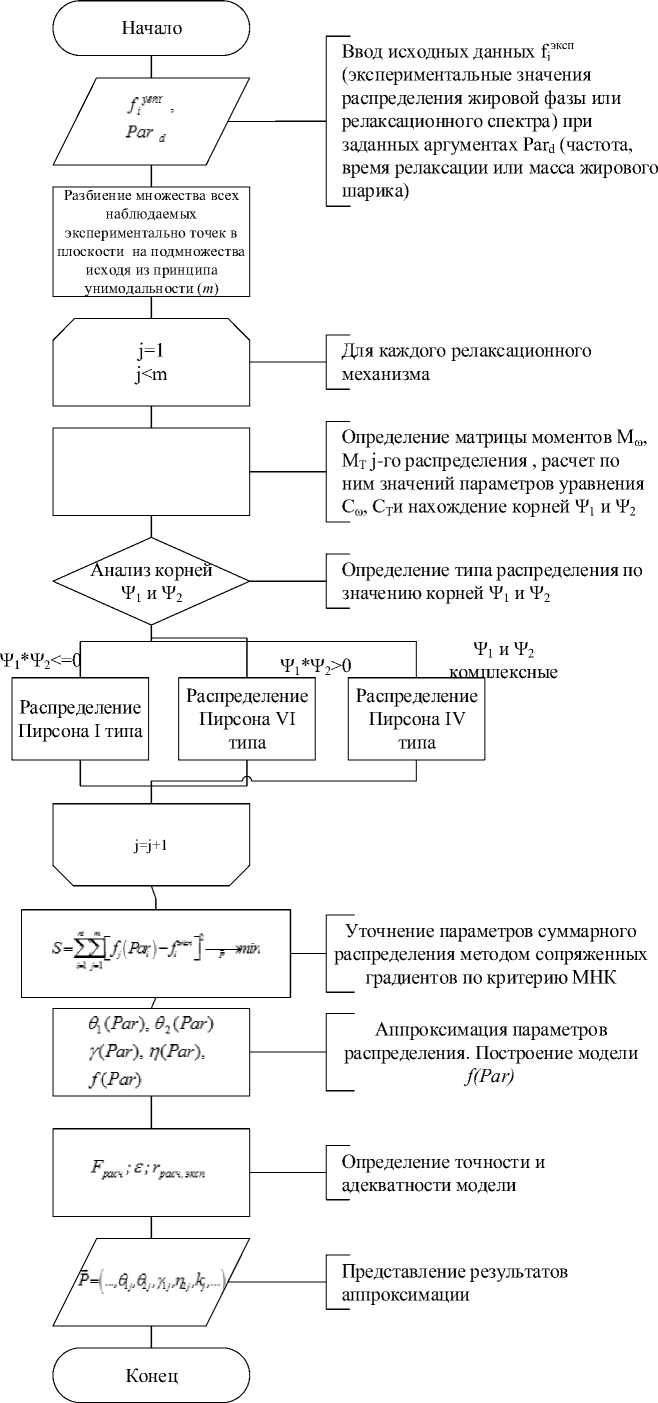
Рисунок 1. Алгоритм построения математической модели

ление его корней у_ю , V T .

По проведенным экспериментальным исследованиям установлено, что полученные корни уравнения (2) – вещественные числа разных знаков. Поэтому для моделирования спектра времен релаксации необходимо использовать бета-распределение первого рода:

H ^ ) = У ⁽ т ) - ■ (1 - у ⁽ т )) - ² к ■ B ( - 1 , - ₂)

где s1, s2 – параметры рассматриваемого распределения; y(τ) - аргумент; B(s1,s2) - значение полученной бета-функции.

Параметры для распределения вычисляются по формулам:

c - a х, =-----1---------

¹    B 2 ( c + c 2 ) ,

^- 2 =

c ₂ - a

B 2 ( c i + c 2 )

Аргумент распределения можно определить по формуле:

У ( т ) = ^-Г ¹ ,              (10)

где 1 1 = ^ - с 1 , 1 ₂ = с 1 + с ₂.

Для того чтобы идентифицировать параметры модели релаксационного спектра был использован среднеквадратичный критерий:

^ = f ( H( т _i ) э^ксп - H( т _i ) расч ) ²----- >

^- 1 , ^- 2 , k ^{, 1} 1 ^{, 1} 2

■> Ш1П

При проведении экспериментальных исследований использовано 42 образца молока с различным массовым распределением жировой фазы вследствие проведения процедуры гомогенизации при разных давлениях.

Необходимо заметить, что в процессе параметрической идентификации использованы предварительно нормированные данные эксперимента. Переход от абсолютных значений H(τ) к нормированным вызван тем, что площадь под кривой распределения жировой фазы должна быть равна 1, однако условие J H(т)dт = 1 не тШ1П выполняется, поэтому для дальнейшего расчета массового распределения жировой фазы по спектру времен релаксации необходимо осуществить нормировку исходных данных.

Для чего необходимо соблюдение следующего условия:

N f н (т) = 1,               (12)

i = 1

где N – количество точек измерения.

Для чего необходимо осуществить введение дополнительного нормирующего коэффициента k норм , который обеспечивает выполнение равенства (4):

k норм    N                      ⁽¹³⁾

f ^н ( т , ) i = 1

При дальнейших расчетах используемые экспериментальные значения спектра времен релаксации подразумеваются как нормированные значения.

На рисунке 2 представлены экспериментальные значения распределений жировой фазы молока до процесса гомогенизации и при разных давлениях проведения процесса. Приведенные данные показывают увеличение содержания низкоразмерных фракций с увеличением давления гомогенизации.

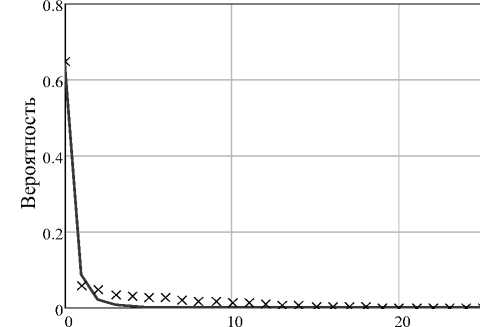
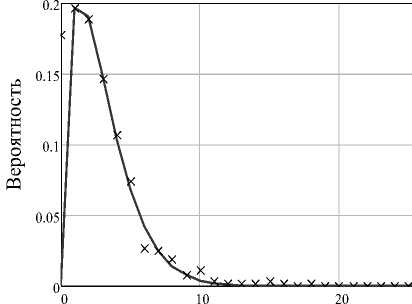
Аппроксимация семейством кривых Пирсона с использованием зависимости структуры (3) позволила качественно верно описать изменение распределения жировой фазы в ходе процесса гомогенизации (рисунки 3, 4, 5). Из представленных графиков видно, что в начале процесса гомогенизации вид распределения имеет ярко выраженный экстремум, благодаря чему распределение можно считать унимодальным. В этом случае математическая модель на основе кривых Пирсона с приемлемой погрешностью (порядка 18%) описывает распределение жировой фазы.

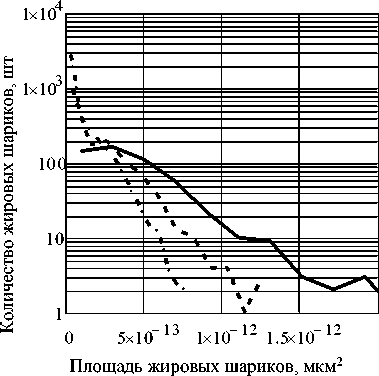
– – негомогенизированное молоко, - . - . - – гомогенизированное при давлении 90 и 180 МПа, соответственно

Рисунок 2. Сравнительные распределения жировых шариков в объеме пробы по диаметру

Диаметр жировых шариков, мкм

̶ кривая аппроксимации, ××× экспериментальные данные

Рисунок 5. Аппроксимация экспериментальных данных распределения жировых шариков гомогенизированного молока при давлении 180 МПа ДУ Пирсона

Диаметр жировых шариков, мкм

̶ кривая аппроксимации, ××× экспериментальные данные

Рисунок 3. Аппроксимация экспериментальных данных распределения жировых шариков негомо-генизированного молока ДУ Пирсона

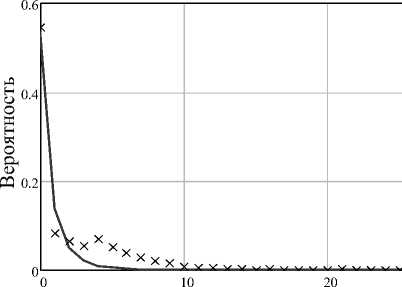
Диаметр жировых шариков, мкм ̶ кривая аппроксимации, ××× экспериментальные данные

Рисунок 4 Аппроксимация экспериментальных данных распределения жировых шариков гомогенизированного молока при давлении 90 МПа ДУ Пирсона.

Однако в ходе процесса гомогенизации вид кривой распределения изменяется, и экстремум смещается к левой границе области определения функции распределения фазы по размерам. Кроме этого, ввиду наличия как гомогенизированной, так и негомогенизирован-ной части в общем объеме начинает проявляться остаток негомогенизированного молока в виде небольшого локального экстремума. В этом случае для того, чтобы достигнуть приемлемого уровня отклонений модельных данных от экспериментальных в математическую модель приходится вводить вторую моду. Такое усложнение модели не только увеличивает в два раза количество её параметров, но и усложняет интерпретацию результатов измерений в системе управления и ЛПР.

Проведенные исследования показали возможность качественного описания изменения объемного (массового) распределения жировой фазы в молочных продуктах с использованием семейства распределений Пирсона. Для более точного описания необходимо вводить в математическую модель описание второй моды или использовать описание функции распределения статистическими моментами.

Вестник ВГУИТ, №2, 2015