Индуктивный порог формирования алгоритмического процесса решения математических задач

Algorithmic process, inductive limit, trajectory of learning activity, strategy of problem solving search. Independent student work on the formation of algorithmic process of the transformation of curves of the second line is analyzed. The histograms of algorithms and inductive thresholds are experimentally constructed. The trajectories of operational steps of the performance of educational actions in accordance with a trial and error method at the beginning of learning and algorithmic process at the end of learning are obtained. The analysis of the function of selflearning activities of students and the strategies of problem solving search are offered.

m

e

В

процессе научения студентов решению алгоритмических задач можно обучать алго-

ритмам с учителем и без учителя. Во втором случае реализуется способ обучения алгоритмической деятельности, описанный Л.Н. Ланда следующим образом «…не обучать ни алгоритмам, ни методам неалгоритмического характера, ни правилам, а ставить человека в проблемную ситуацию, сталкивать его с задачами, рассчитывая на совершенно самостоятельное нахождение (открытие) алгоритмического процесса (алгоритмической процедуры) в ходе самонаучения» [Ланда, 1966, с. 523]. Студенту не сообщается напрямую, как поступить или какое действие предпринять. Он сам на основе собственного опыта узнает, какие действия приводят к целевому состоянию задачи. Действия обучающегося определяются не только сиюминутным результатом, но и последующими действиями и случайными подкреплениями. Эти два свойства (метод «проб и ошибок» и подкрепление) являются основными характери-

стиками компьютерной системы интерактивного управления учебной деятельностью студентов, обучающихся решению алгоритмических задач [Дьячук, Пустовалов, Суровцев, 2008. с. 258–263].

Как указывает Дж. Люгер, «… обучение с подкреплениями не определяется конкретными методами обучения. Оно характеризуется действиями объекта в среде и откликом этой среды» [Люгер, 2003, с. 435]. Такое обучение отличается от обучения с учителем, который напрямую инструктирует или тренирует обучающегося. При обучении с подкреплением студент обучается сам с помощью метода проб и ошибок и обратной связи. Для достижения целей обучения студент сам определяет тактику и стратегию своей деятельности. Чтобы оптимизировать процесс научения студент не только опирается на свои знания, но и исследует пространство состояний алгоритмических задач данного типа с тем, чтобы найти правильный алгоритм поиска решения задач. Очевидно, что одна решенная задача не даст нуж-

к m

S к

1 Работа выполнена в рамках Программы стратегического развития КГПУ им. В.П. Астафьева, № 2011-ПР-217, проект 14/12.

и и и m

к

m к и

w

s и

к

к

ного результата в исследовании алгоритмического процесса поиска решения задач. Для получения обучающимся достоверной информации об алгоритме решения задач проводимые им исследования должны многократно повторяться.

Поскольку студенту не сообщается алгоритм решения задачи, то его действия недетермини-рованы и требуют от студента в процессе решения задач самостоятельного нахождения действий и самостоятельного принятия решений. Незнание алгоритма и, как следствие этого, недетерминированность действий, незнание (или неточное, неполное знание) того, какие операции надо в том или ином случае производить, чтобы решить задачу, и является, по-видимому, той существенной особенностью, которая позволяет назвать такую деятельность самостоятельной.

Теоретический анализ. Интерактивное управление неопределенностью проблемной среды алгоритмических задач позволяет варьировать степень самостоятельности или творчества в поиске решения задач. Научение решению задач подразумевает обобщение на основе опыта. Полученный ограниченный опыт решения задач обучающийся должен корректно распространить на все множество задач данного типа. Количество задач, которые необходимо решить обучающемуся, прежде чем сделать обобщение, является индуктивным порогом. Индукция, или способность человека к обобщению на основе ограниченного множества решенных примеров, является, как указано в [Люгер, 2003, с. 435], одной из фундаментальных задач обучения. Соответственно, индуктивный порог является важной процессуальной характеристикой научения решению алгоритмических задач.

Рассмотренная в [Дьячук, Пустовалов, Суровцев, 2008. с. 258–263] компьютерная система управления учебной деятельностью ставит обучающегося в проблемную ситуацию поиска решения задач. При этом студент самостоятельно формирует алгоритмический процесс решения задач.

В качестве примера возьмем задачи по конструированию эллипса, заданного уравнениями:

x cosa+y sina+x0 = x x sina-y sina + y0 = y-

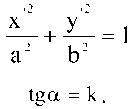
На экране дисплея в нештрихованной системе координат имеется заготовка-объект в виде окружности единичного радиуса. Управляющими кнопками студент может производить различные операции с этим объектом: растягивать, сжимать, поворачивать, перемещать по горизонтали и вертикали. Задача состоит в том, чтобы сконструировать эллипс, соответствующий уравнениям задачи. Рандомизация параметров эллипса k, a, b, x0, y0 позволяет получить серию аналогичных задач по конструированию эллипса. В пространстве состояний задачи конструирования эллипса случайным образом генерируются целевые состояния. Начальное состояние задач одно и то же. Это единичная окружность, описываемая уравнением x² + y² + 1 .

Операции по преобразованию эллипса про- нумеруем следующим образом: 1

–

смеще-

ние графика вдоль оси OX; 2 – смещение графика вдоль оси OY; 3 – сжатие-растяжение полуоси а; 4 – сжатие-растяжение полуоси b; 5 – операция поворота эллипса; 6 – ввод ответа. Если деятельность студента приобретает алгоритмический характер, то можно делать вывод о том, что у студента, по крайне мере, сформирована алгоритмическая последовательность (алгоритмический процесс) при решении задач по конструированию кривых второго порядка. Но при этом студент может не осознавать алгоритмический процесс как некоторую систему предписаний. Лишь когда алгоритмический процесс осознается и формулируется в виде некоторой системы правил или указаний, можно говорить о нахождении студентом не только алгоритмического процесса, но и соответствующего алгоритма предписания [Ланда, 1966, с. 523].

Экспериментальная часть. На рис. 1 а, б показаны графики пооперационного выполнения действий в процессе решения задачи в начале (метод проб и ошибок) и в конце научения (алгоритмический метод). По завершении научения деятельность студента стала носить строго упорядоченный (алгоритмический) характер. При этом все совершенные студентом действия правильные (рис. 1 а, б).

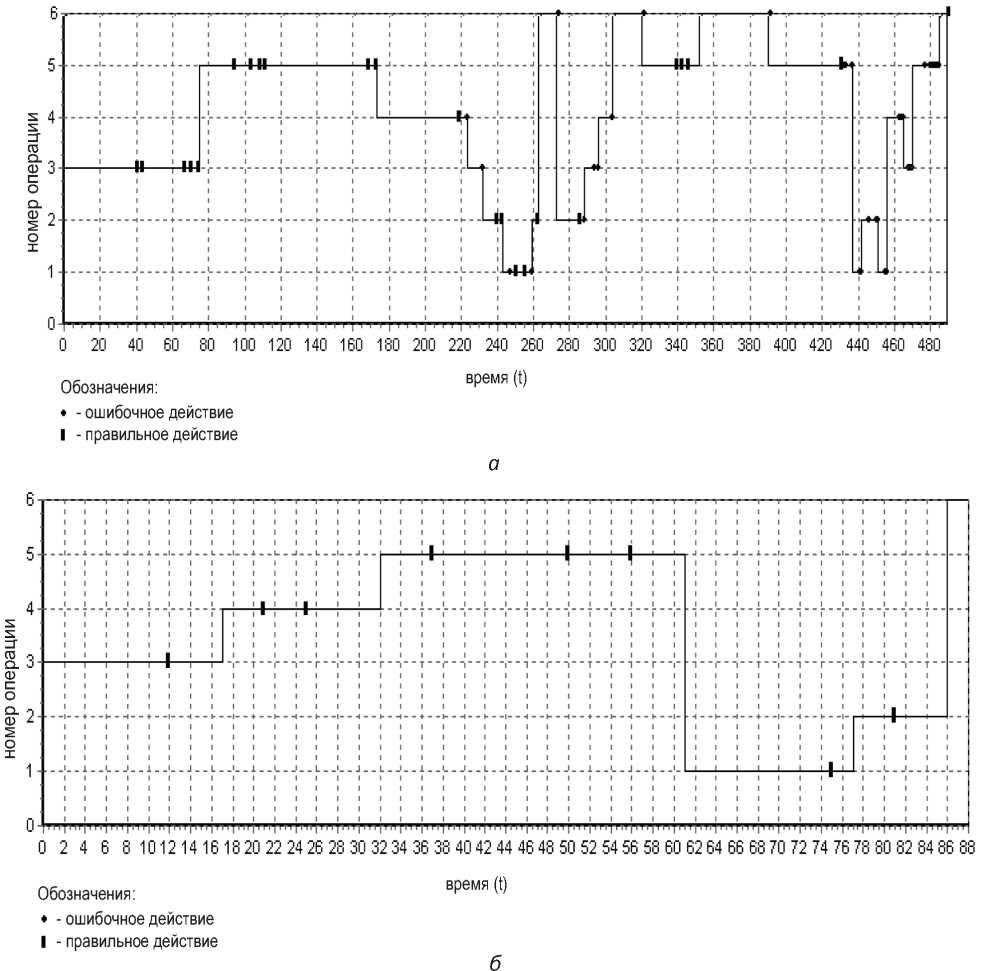
Рис. 1. График пооперационного выполнения задания в зависимости от времени: а – в начале; б – в конце научения решению алгоритмических задач

о к к

G

к

К

к к

Из

анализа рис. 1 б можно сделать вывод

о том, что у студента сформирован алгоритмический процесс решения задачи, но не факт, что им осознается алгоритмический процесс в виде алгоритма предписаний. При анализе формулировок алгоритмических предписаний, данных студентами, можно отметить выстроенную обучающимся последовательность операций. Однако почти в каждом пункте предписаний отмечается незавершенность указаний. Правила сформулированы нечетко и логически не завершены. Если кто и сможет пользоваться таким предписанием, так это только авторы. Тем не менее совершенно очевидно, что самостоятельная работа студентов по научению алгоритмической деятельности развивает творческий потенциал студентов.

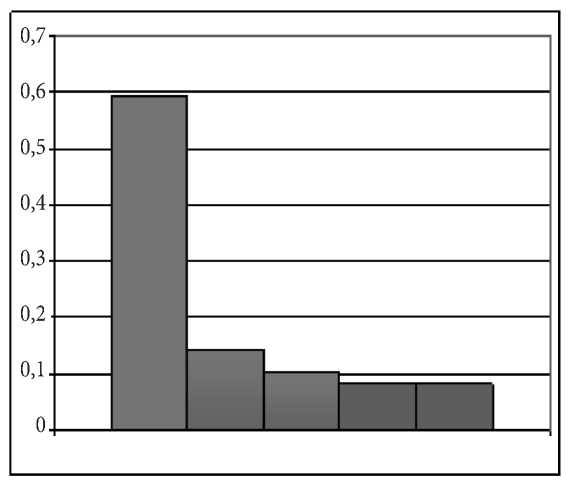
На рис. 2 а приведено распределение студен-

тов по типам алгоритмических последовательностей: xyabtg; tgabxy; abtgxy; tgxyab; abxytg выполняемых операций (x, y – операции смещения; a, b – операции растяжения-сжатия; tg – операция поворота), выработанных в результате самостоятельной учебной деятельности. Видно, что большинство студентов (около 60 %) выбирают последовательность xyabtg, то есть вначале студенты выполняют операции смещения эллипса вдоль осей координат OX и OY, затем выполняют операции растяжения и сжатия полуосей a, b и завершают преобразование графика операцией поворота.

Как уже говорилось, индуктивный порог [2] равен количеству упражнений (задач), выполнив которые, студент самостоятельно находит (открывает) алгоритмический процесс в ходе самонауче-ния [Дьячук, Пустовалов,Суровцев, 2008]. Если этот

о о S

S к

«

о

S

S

К

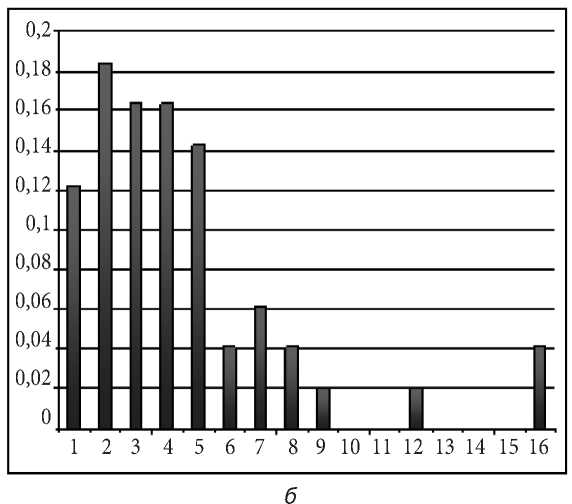
процесс формулируется в виде некоторой системы правил или указаний о том, как надо в определенных условиях действовать, то можно говорить о нахождении обучающимся не только требуемого алгоритмического процесса, но и соответствующего алгоритма предписания. На рис. 2 б приведена гистограмма распределения студентов по индуктивным порогам. По вертикали гистограммы отложена относительная доля студентов, имеющих индуктивный порог, заключенный в интервале от 8*(i -1)+1 до 8*i, где i – номер группы студентов. Первый столбец гистограммы соответствует индуктивным порогам, лежащим в интервале от 1 до 8 задач, индуктивный порог для последней 16 группы студентов отвечает интервалу от 121 до 128 задач. Максимум гистограммы распределения студентов по индуктивным порогам лежит в интервале от 9 до 16 задач (рис. 2 а, б).

Следует отметить, что далеко не все студенты достигают индуктивного порога при научении решению алгоритмических задач. В выборке студентов, участвующих в эксперименте, 40 % испытуемых не сделали обобщение (то есть не достигли индуктивного порога) и, соответственно, не смогли организовать безошибочную алгоритмическую деятельность. При этом временного ограничения на процесс научения не накладывалось.

В проведенном эксперименте доля студентов (женского пола), достигших индуктивного порога от общего числа студенток, участвующих в нем, составила 53 %. Доля студентов (мужского пола), достигших индуктивного порога от общего числа студентов мужского пола, существенно больше и равна 83 %. Отсюда можно сделать вывод о том, что юноши более способны к алгоритмической деятельности, чем девушки, что обусловлено доминированием у них левополушарного мышления, отвечающего за алгоритмическую деятельность.

Стратегии решения задач, которыми пользуется человек, выражают поиск операций для достижения определенных результатов. Для человеческого мышления в процессе решения задачи не характерно использование какого-либо вида поиска в чистом виде, поэтому речь идет о доминировании одного из них, что определяет индивидуальную когнитивную стратегию личности в решении задачи. Вид поиска решения задачи может изменяться по мере обучения в ходе решения задач.

Когнитивные стратегии решения задач подразумевают разработку плана, выражающего один из возможных способов решения, который человек формирует или выбирает из известных ему для решения задачи. Стратегия строится на основе обобщенных программ действия, которыми располагает человек. В условиях работы над задачей действия человека заключаются в поиске её решения. Поиск решения – это отыскание принципа, логики решения, в соответствии с чем выполняются

а

Рис. 2. Гистограмма: а – распределение студентов по типам алгоритмов: слева направо xyabtg; tgabxy; abtgxy; tgxyab; abxytg (x ,y – операции смещения; a, b – операции растяжения-сжатия; tg – операция поворота); б – распределения студентов по индуктивным порогам (номер столбца гистограммы определяет соответствующий интервал индуктивного порога, см. текст)

те или иные операции, о которых нельзя заранее сказать: приведут ли они к требуемому результату или не приведут. Л.Л. Гурова выделяет четыре вида поиска решения, которые не всегда резко разграничиваются в конкретном решении, но различны по существу [Гурова, 1976].

Первый вид поиска – поиск посредством систематических проб, по порядку обследующих все возможные ходы на каждом этапе решения.

Второй вид поиска – это случайный поиск, при котором направление решения определяется по какому-нибудь случайному критерию.

Третий вид поиска – выборочный поиск. В этом случае очередной ход, действие выбирается только на основании предыдущего. В психологии мышления такой метод получил название метода проб и ошибок: если проба привела к ошибке, опробуется другой ход.

Четвертый вид поиска – интеллектуальный (селективный) – когда действия человека зависят от сложившейся ситуации и он свободен в принятии решения о том, какой должна быть следующая попытка. Происходят оценка возможных ходов и выбор лучшего из них. В этом состоит отличие селективного поиска от метода проб и ошибок, который хотя и может улучшать решение, но в сложных задачах улучшение (и, следовательно, решение) вряд ли будет достигнуто.

Для интеллектуальной деятельности человека наиболее характерны третий и главным образом четвёртый виды поиска решения. Метод полного перебора вариантов человек использует редко, только на отдельных этапах решения в комбинации с другими методами поиска. Это связано с тем, что мышлению человека не свойственна абсолютная систематичность (иначе он не был бы самоорганизующейся системой), кроме того, решающему задачу большей частью не известны все возможные варианты решения (за исключением самых несложных задач). Использование методов случайного и выборочного поиска допускает возможность самообучения и, следовательно, самоорганизации. Отсутствие строго определенного регламента создает свободу во взаимодействии со средой.

Стратегии поиска решения задач также изучались на основе применения интерактивных систем управления учебной деятельностью

[Дьячук, Пустовалов, Суровцев, 2008; Дьячук П.П. (мл.), Дьячук И.П., 2011].

Для определения вида поиска была выбрана функция уровня самостоятельности обучающегося (i), напрямую зависящая от уровня информационной энтропии испытуемого (i=1- Н(p)). На рис. 3 а приведена функция уровня самостоятельности деятельности обучающегося в зависимости от номера выполненного задания. В данном случае она же является экспериментальной кривой научения.

Эмпирически было получено, что при 0.7<Н<1 поиск решения задачи испытуемые осуществляли методом проб и ошибок. При 0.33<Н<0.7 испытуемые реализовали выборочный поиск решения задач. Он характеризуется определенной структурой последовательности выполняемых операций, но сохраняется неопределенность в принятии решения о прекращении или продолжении операции.

Если 0<Н<0.33, то осуществляется алгоритмический процесс поиска решения задач. В процессе эксперимента испытуемые выполняли от 20 до 70 (рис. 3 а, б) заданий, поэтому у нас есть возможность проследить динамику изменения стратегии поиска решения в зависимости от процента выполненных заданий по всей выборке испытуемых. Эти результаты отражены на рис. 3 б.

По оси абсцисс отображается процент заданий, по оси ординат – количество студентов, применяющих указанную стратегию поиска решения.

В заключение отметим, установлено, что в продуктивном, развивающем обучении ведущую роль играет учебная деятельность по научению решению задач. Показано, что обучающийся самостоятельно реализует свою целевую функцию научения на основе подкреплений своих действий со стороны проблемной среды алгоритмических задач. В качестве целевой функции научения выступает энтропия деятельности обучающегося H.

Основной задачей системы интерактивного управления учебной деятельностью является содействие адаптации студентов к проблемным средам. Мерой адаптации является величина энтропии деятельности, которая по мере формирования алгоритмического процесса уменьшается до нуля.

Рассмотрен конкретный пример интерактивного управления учебной деятельности по научению решению задач по конструированию кривых второго порядка. Машинная обработка продуктов деятельно- m

e

к m

S к

и и и m

к

m к и

w

s и

к

к

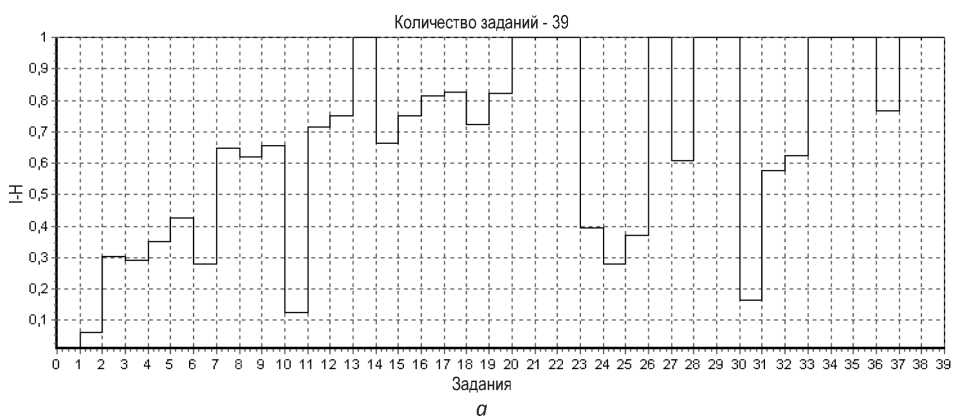
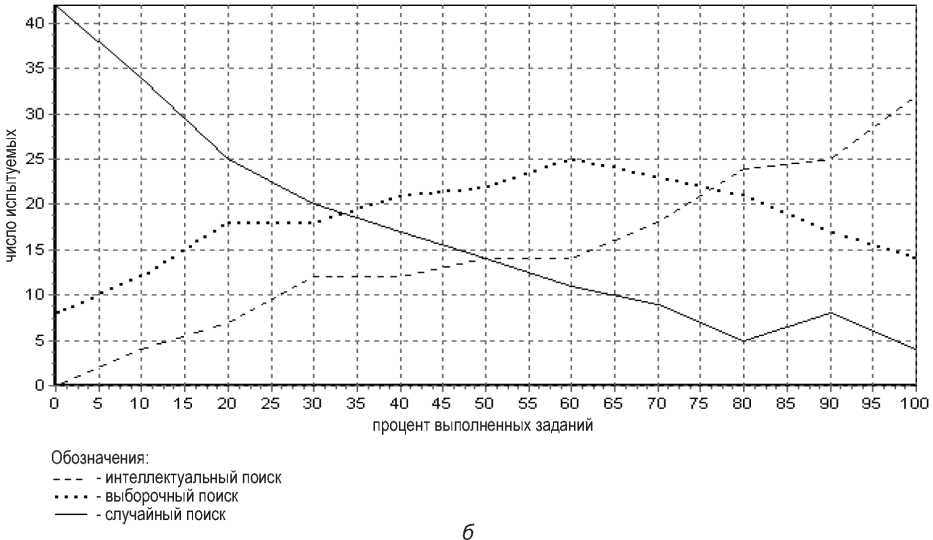
Рис. 3: а – функция уровня самостоятельности деятельности обучающегося в процессе научения решению задач в зависимости от номера задания;

б – динамика изменения стратегии поиска решения в зависимости от процента выполненных заданий (сплошная линия – случайный поиск; линия, изображенная точками, – выборочный поиск; штрих-пунктирная линия – интеллектуальный поиск, отвечающий алгоритмическому процессу)

сти позволила получить гистограмму распределения индуктивных порогов учебной деятельности студентов и гистограмму распределения алгоритмических последовательностей выполнения операций, а также построить экспериментальные кривые научения и графики пооперационного выполнения задания в зависимости от времени и номера задания. В результате группового статистического анализа у испытуемых выделено три вида поиска решения задач: случайный, выборочный и избирательный. Установлено, что в процессе научения стратегия поиска решения задач изменяется в направлении алгоритмизации или интеллектуализации деятельности.