Inelastic interaction and splitting of strain solitons propagating in a granular medium

Математические модели, описывающие распространение и взаимодействие нелинейных волн в распределенных системах, к которым относится и зернистая среда, принято подразделять на интегрируемые и не интегрируемые методом обратной задачи рассеяния [1]. На сленге специалистов упомянутые модели называются, соответственно, «интегрируемыми» и «неинтегрируемыми» системами.

Во многих работах (см. например [1, 2]) аналитически и численно показано, что в «интегрируемых» системах локализованные волны (солитоны) ведут себя подобно частицам: при столкновении они сохраняют свою индивидуальность и приобретают лишь сдвиг фаз (имеет место «упругое» взаимодействие). Этот факт подтвержден экспериментами, где объектами исследования были нелинейные волны в плазме, жидкость с пузырьками газа, а также электромагнитные волны [3, 4].

Для «неинтегрируемых» систем, наряду с упругим, характерен и другой сценарий поведения локализованных волн. При обгоне друг друга солитоноподобные волны излучают часть своей энергии в виде квазилинейных волновых пакетов (наблюдается неупругое взаимодействие) [5].

В работе [6] (ее русский перевод можно найти в книге [7]) экспериментально обнаружены не только эффекты неупругой связи, но и эффекты расщепления сильно нелинейных волн, когда после взаимодействия из волнового пакета выделяются дополнительные солитоноподобные волны. Эффекты расщепления были найдены при встречном столкновении сильно нелинейных волн, распространяющихся по резиновой ленте.

В публикуемой работе методом структурного моделирования [8] получена система нелинейных уравнений в частных производных, описывающая волновые процессы в зернистой среде и позволяющая исследовать особенности взаимодействия локализованных сдвиговых волн. Данная математическая модель относится к классу «неинтегрируемых» систем.

В настоящее время отсутствуют какие-либо регулярные методы построения аналитических решений, способных отобразить как обгонное, так и встречное взаимодействие солитоноподобных волн, поэтому

в предлагаемой работе приводятся результаты только численного моделирования. Процессы, происходящие при встречном столкновении, строго говоря, не могут быть представлены эволюционными уравнениями одноволнового приближения [9], и нужно привлекать полные уравнения нелинейной динамики, учитывающие волны, движущиеся в обоих направлениях. Такие уравнения, как правило, не интегрируемы, и их решения описывают уединенные волны, не являющиеся солитонами в строгом математическом смысле [1], однако для простоты также будем называть их солитонами.

2.    Дискретная модель

Рассмотрим элемент среды — цепочку, состоящую из однородных круглых частиц — зёрен массой M и диаметром d . В исходном состоянии частицы сосредоточены в узлах решетки, и расстояние между центрами масс соседних частиц вдоль оси x равняется a . (Рис. 1). При движении в плоскости каждая частица с номером N = N ( i ) имеет три степени свободы: трансляционные — смещение центра масс u i и w i по осям x и у , и ротационную ф i — поворот относительно центра масс (Рис. 2). Кинетическая энергия частицы N ( i ) описывается формулой

T i = M ( и 2 + w , ²) /2 + J ф 2/ 2,

где J = Md ²/8 — момент инерции частицы относительно оси, проходящей через центр масс.

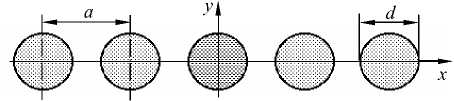
Рис. 1. Цепочка из круглых частиц

Считается, что частица N взаимодействует лишь с двумя ближайшими по цепочке соседями, центры масс которых в начальный момент времени удалены от центра масс частицы N на расстояние a по оси x (Рис. 2). Центральные и нецентральные взаимодействия соседних зёрен моделируются упругими пружинами трех типов [8]: центральными (с жесткостью K ₀ ), нецентральными (с жесткостью K ₁ ) и диагональными ( K ₂ ). Взаимодействия при растяжении–сжатии материала характеризуются центральными и нецентральными пружинами. Через пружины типа K ₁ передаются также моменты при поворотах частиц. Пружины с жесткостью K ₂ описывают реакцию частиц на сдвиговые деформации в материале. Для удобства дальнейших вычислений будем считать, что точки соединения пружин K ₀ лежат в центрах круглых частиц, а пружин K 1 , и K ₂ — в вершинах квадрата со стороной h = d /V2, вписанного в окружность (Рис. 2).

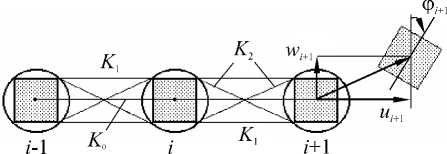
Рис. 2. Схема силовых взаимодействий между частицами и кинематика

Предполагается, что элементарной ячейкой рассматриваемой решетки является частица вместе с прикрепленными к ней десятью пружинами трех вышеуказанных типов, а смещения зёрен малы по сравнению с размерами такой ячейки. Воздействие частиц друг на друга при отклонениях от положения равновесия определяется относительными удлинениями пружин (Рис. 2). Потенциальная энергия, обусловленная взаимодействием частицы N c восемью ближайшими соседями по решетке, описывается формулой

2  44

и ₌ 11 у K I_D^ ₊ у K_D^ ₊ у _ 2__D^ I

U N I ^ D 0 n + ^ ^ D 1 n ⁺ ^ D 2 n I,

2 X. n=1 2          n=1 2          n=1 2 J где Dn (I = 0,1,2,3) — удлинения пронумерованных в произвольном порядке пружин четырех типов, соединяющих частицу с ее соседями, причем удлинения центральных пружин зависят от изменений расстояний между геометрическими центрами круглых частиц, а растяжения остальных пружин — от изменений расстояний между вершинами квадратов, вписанных в окружности (Рис. 2). В выражение (2) входит дополнительный множитель 1(2, поскольку потенциальная энергия каждой пружины делится поровну между двумя частицами, соединенными этой пружиной.

Обозначив A u = u i - u i _{- 1}, вычислим удлинения пружин D n в приближении малости величин A u ~ A w ~ а б , Аф ~ е ^3/2 , Ф ~ Ve , где Ф = (ф _t + ф ) /2 « л/ 2 и е — мера деформации ячейки. После подстановки этих выражений в (2) составим функцию Лагранжа L = T - U i для частицы с номером N ( i ) с точностью до слагаемых порядка е ^2,5 включительно. Затем с помощью уравнений Лагранжа 2-го рода из (1) и (2) можно получить нелинейные дифференциально-разностные уравнения, описывающие динамику рассматриваемой решетки [10]. Однако в данной работе обсудим лишь континуальное приближение предложенной модели.

3.    Континуальное приближение

В случае длинноволновых возмущений, когда X » а (где X — характерная длина акустической волны), лагранжиан рассматриваемой среды с микроструктурой имеет вид:

L = M ( u t ⁺ w ⁺ R ²ф² ) ^- MM [ c ² u 2 ⁺ c ² w X ⁺ R ² c з² ф Х ^{+ 2} Р ²⁽ W x ф + ф ^{2) +}

+а ₁ u x + а ₂ u x w x + а ₃ u _x ф ² + а ₄ u _x w _x ф! .                                  (3)

Производные по времени t и координате x обозначены соответствующими индексами. С помощью вариационного принципа Гамильтона-Остроградского из лагранжиана (3) выведем систему нелинейных дифференциальных уравнений, описывающих динамические процессы в одномерной решетке с круглыми частицами в узлах:

u t - c 1² u xx = ТТ" ^{(3 а} 1 u x ^{2 +а} 2 w ^{2 +а} 3 ф ^{2 +а} 4 w x ф ), 2 д x

• .      1 д _

  
  

w„ - c2 w„ - в ф, =--(2а2urwr +а4u m), tt 2 xx          x                   2 x x 4 x

• 2    д x

R ²⁽ ф tt ^- c 3² ф xx ) + P ²⁽ w x ⁺ N) =^{- 2 а} 3 u x ф^-а 4 u x w x ■

Здесь введены обозначения: c i ( i = 1, 2, 3) — скорости распространения, соответственно, продольной и сдвиговой волн, а также волны микровращений; в — параметр дисперсии; а i ( i = 1,...,7) — коэффициенты нелинейностей; R = d ^8 — радиус инерции частицы. Заметим, что линейные части уравнений (4) совпадают с линейными уравнениями одномерного континуума Коссера [11-13].

Квадраты скоростей упругих волн [14] и коэффициенты нелинейностей выражаются через силовые постоянные K ₀, K 1 , K ₂, период решетки а и размер частицы h = d /V² ( d — диаметр частицы) следующим образом:

c2 = —— k + 2 K +■

¹ M ( ^{0     1}

₂ _ a ² f      2 h ²

2( a - h ) ² K

( a - h ) ² + h ^{2 2}

c ²    M ( ( а - h ) ² + h²

K 2 1=в ² ,

2 _ a2 h2 Г           a2

cl               -KI +

• ³    2 MR ² ( ¹ ( a - h ) ² + h ^{2 2} J

M а , = ^2- a ³( a - h ) h ², r ⁴

a 3

M а2 = K 0 a2 + K1-----+    a 3( a - h)(a2 - 2 ah - h2), a - h r4

M a ₃ = K 1 ah— + K 2 ah- (2 h - a )(5 ah - 2 h ² - a ²), a - h r ⁴

2 a ² h 2 a ³ h

M a ₄ = K 1---- +-- —K ₂ ( 5 h - 5 ah + a ) .

a - hr ^{4      v}                '

Здесь r = д/( a - h ) ² + h ² — длина пружин с жесткостью K ₂ (Рис. 2) в начальный момент времени.

4.    Низкочастотное (двухмодовое) приближение

Теоретические оценки [14] и экспериментальные данные [15] показывают, что ротационные волны в твердых телах существуют в области высоких частот ( > 10 9 ^ 10" Гц), где проведение акустических экспериментов сталкивается с большими техническими трудностями. Тем не менее информацию о микроструктуре среды можно получить по акустическим измерениям даже на сравнительно низких частотах (10 6 + 10 7 Гц), например в случае, когда ротационные волны в среде не распространяются. Поэтому рассмотрим низкочастотное приближение уравнений (4), в котором микроповороты частиц среды зависят от поля смещений. Связь между микроповоротами ф и смещениями и и w можно найти из линейной части третьего уравнения (4) методом последовательных приближений. Так как в этом уравнении главную роль играет слагаемое р ² ( w x + 2 ф ), а следующим по порядку малости является второе слагаемое линейной части уравнения R ² ( ф _tt - c ₃ ² ф xx ), то в первом приближении

ф ( x , t ) ~ w x /²,

а во втором приближении переменную ф можно выразить через w _x и ее производные следующим

1 д w . R ² ( д ³ w образом: ф ( x , t ) ®--- - +--- ---- x-

2 д x 4 р ² I д x д t ²

—

2 д3wr

c32      x дx3

.

Учет этой связи ведет к «замораживанию» ротационной степени свободы и, как следствие, исключению ф из системы (4). В результате система (4) вырождается в двухмодовую систему — без уравнения для ротационной моды. При этом в среде с двумя трансляционными степенями свободы остаются и два типа волн — продольные и сдвиговые (поперечные). Лагранжиан L с учетом связи (6) принимает вид

т M Г 2    2 R2 2^ M Г 2 2  . 2 Р\ 2 R 2 2 2      3        2

,

L = — и, + w. + — w«--cu г + (c г--) w, + — c3 w„ + ai и r +Y urwr

2t t 4xt 21x 22x 43xx 1x x x где Y = a2 +a3/4 -a4/2, причем из трех последних равенств (5) следует, что у> 0. Видно, что в лагранжиане (7) появляются дополнительные слагаемые, содержащие вторые производные от поля смещений. Подобных слагаемых нет в классическом варианте теории упругости, но именно в них и сохраняется информация о микроструктуре среды. Слагаемые со смешанными производными по времени и пространству wxt учитывают вклад в кинетическую энергию, вносимый ротационными движениями, а члены с пространственными производными wxx и подобными им описывают вклад напряжений, обусловленных изгибом решетки, в потенциальную энергию. Из лагранжиана (7) можно получить уравнения градиентной теории упругости [16], содержащие слагаемые с производными высокого порядка (в данном случае — четвертого):

u « - c 12 u xx

1 д( 3a1 u2+Y w2)

2       д x

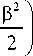
w

R ² д

4 д x

д ² w _{x 2} д ² w _x д t ^{2 3} д x²

д(у uxwx) дx

(8a)

(8b)

Необходимо подчеркнуть, что, несмотря на отсутствие микроповоротов в уравнениях (8a, 8b), микроструктура среды повлияла на коэффициенты уравнений в этом низкочастотном приближении. По сравнению с исходными уравнениями (4) здесь изменился коэффициент перед w _xx : с учетом второго соотношения (5) он фактически уменьшился вдвое.

5.    Солитонные решения

Рассмотрим продольную статическую деформацию зернистой среды (8) и сдвиговую волну в ней. Тогда из уравнения (8a) получим уравнение

2           1 д            2 . .    2 "I

- C i U xx =—1 3 a u, + Y w, I , 2 d x     1 x x

которое после интегрирования

преобразуется к виду:

3 a , u x + 2 c 2 u _x + y w 2 = C ,

где C — константа интегрирования. Заметим, что для уравнения в деформациях ненулевая константа интегрирования означает, что среда имеет предварительное напряжение, которое никак не влияет на дальнейшие исследования. Таким образом, без ограничения общности в (9) можно положить С = 0, и тогда продольная деформация может быть выражена через сдвиговую одним из двух способов:

u X ¹’ =

—

Л W 2 c ₁ ^{2 x}

(2)       ² c l       ^Y 2

или u () =--^L + —₇ w_Y.

^x     3 a 1 2 c ^x

При первом способе уравнение для поперечной моды (8b) принимает вид

I 2 PI R (           2       \

W„ — СT--w rr-- ( W”xx — c 3 Wxxxx ) tt 2 xx               ttxx 3 xxxx

Y ² d w 3

2 c 2 d x ’

(10a)

при втором

w tt

—

c ₂

—

—

2 с Y

3 a ,

w

—

R ² — w

4 ttxx

—

c ² w xxxx ) =

Y ² d W 3

2 c d x

.

(10b)

Уравнения (10a) и (10b) можно записать единообразно:

R² l 2     A - Y^{2 d} W 3

w tl ^{—a W}xx 4" ( w ttxx ^— c 3 w xxxx )= + 2 c r ”d x" ,                                (11)

где коэффициент a принимает одно из двух возможных значений:    a ⁽¹⁾ = c 2 — в ² /2,

a ⁽²⁾ = c ₂ ² — 0 2/ 2 — 2 c 2 Y/ ( 3 a 1 ) .

Приведем уравнение (11) к безразмерному виду. Для этого используем безразмерные величины перемещения, координаты и времени: W = w/w ₀, x = x]X , ^f = t/T , и получим следующее уравнение:

W-tt

T ² .     R ² T ² d ² I 1 .      2 1             Y 2 T ² w ₀ ² d W 3

— a-- X W=--;--x —x AV- — c --X W_s-- 1---:--; --.

X ² xx   4 X ² d x ² ( T ² “   ³ X ²     J     2 c 1²   X ⁴   d 5c

Положим X2/T2 = a , X2 = R2/4, тогда уравнение (12) преобразуется к виду wti

—

w xx

d ² d 5c ²

—

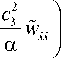
= _ 6Y ² W 2

⁺ c 1² a R²

[ i v 2 i v xx ] .

Пусть 6 y ² w 0 /( a c 1² R ² ) = 1, откуда w 2 = a R ² c 1² Д 6 y ² ) или w ₀ = ( Rc 1 /y)707 6 , и (13) запишется как

W- tt

— ( 1 - T V 2 ) eV xx

d ²

W- d x ^{2 (} tt

— c ² w ^ xx ) = 0,

где с2 = c32 /a; знак « + » во втором слагаемом слева соответствует жесткой нелинейности, а знак « — » — мягкой нелинейности. Термины «жесткая» и «мягкая» нелинейности происходят от нелинейного закона Гука для пружин: a = Eе + E'е2, где коэффициент нелинейности E‘ может быть положительным (жесткая нелинейность) или отрицательным (мягкая нелинейность). Из (5) следует, что с2 > 1 как при a = a(1), так и при а = а(2) для всех допустимых значений параметров микроструктуры (0 < ha < —41, K 1 > 0 , 0 < K2 < 2K0).

Далее, введем обозначения w = W , t = t , x = x . Уравнение (14) допускает решения, описывающие солитоны смещения:

W ( t , x ) = ^24 | v ² - c ² 1 arctg ( exp(( x - vt )/ A ) ) ,

где A = ( c ² - v ² )/( 1 — v ² )

— ширина солитона, v — его скорость. Плотность энергии солитона смещения имеет вид:

E = ^- 1 W ² + W ² ± ¹ W 4 + W 2 + c ² W 2 2 t x          x tx         xx

V             6

а полная энергия вычисляется путем простого интегрирования (16):

+x

J Ed ( x - vt ).

-да

Ее зависимость

от скорости описывается формулой:

+да

J Ed ( x - vt ) =

-да

± ( 6 v ⁴ - 5 v ² c ² + v ² - c ² - 1 ) 4 v ² - 1

V v - c

Из решения для смещений простым дифференцированием (15) можно получить выражение для солитона деформации:

U (t, x) =

d W ( t , x ) d x

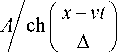
где A = ^6 | v ² -1| — амплитуда солитона. С точки зрения графического представления и дальнейшей интерпретации результатов анализировать солитоны деформации предпочтительнее, чем солитоны смещения, так как при x ± vt ^±да w ( t , x ) ^ 0. Уравнение для солитонов деформации также можно получить из уравнения (14) простым дифференцированием:

д ² и  д ² Г_т и ³ )  д ² fa ² и   ₂а ² и ) _Л

—9---ri и + а— I--т1 —9— c—т 1 = 0

д t ²    д x ² V         3 J д x ² V д t ²        д x ² J

Решения уравнения (14) полностью совпадают с решениями уравнения (19) при условии учета (18).

6.    Дозвуковые солитоны

В системе могут существовать солитоны, соответствующие решению (15) или (18), распространяющиеся со скоростями v , меньшими скорости звука. При этом их амплитуда также вычисляется по формуле: A = ^ 611 - v ²| . На рисунке 3 показана зависимость энергии дозвуковых солитонов, удовлетворяющей (17), от скорости v при различных значениях параметра c ² . Из рисунка видно, что энергия имеет максимум при v = v * = 0,78.

Формальное решение (15) или (18) предполагает существование дозвуковых солитонов с любой сколь угодно малой скоростью, однако численные эксперименты показывают, что солитоны со скоростями, меньшими v * , неустойчивы. График v * от c ² , имеющий горизонтальную асимптоту v * = 0,78 , изображен на рисунке 4.

Уравнение (14) и, соответственно, (19), в отличие, например, от уравнения Кортевега–де Вриза, не имеют бесконечного числа полиномиальных законов сохранения. Такие системы называются «не полностью интегрируемыми», и взаимодействие (столкновение) солитонов происходит в них неупруго. Это означает, что в результате столкновения параметры вторичных (или дочерних) солитонов изменяются: они теряют часть энергии, которая может реализоваться в квазигармоническое излучение и, если ее

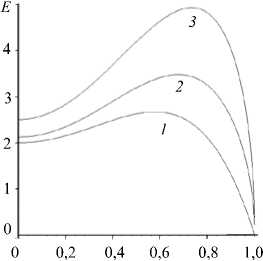
Рис. 3. Зависимость энергии дозвуковых солитонов от их скорости при различных значениях параметра c ² : 1 (кривая 1 ); 2 ( 2 ); 4 ( 3 )

0,76

0.70

0,60

0,58

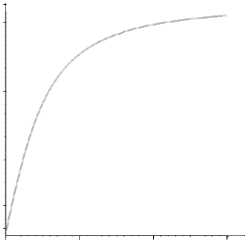
4 с максимального значения

Рис. 4. Зависимость

скорости солитона от c

количество достаточное, в другие солитоны. В этом плане интересно исследовать взаимодействие однополярных и разнополярных солитонов. Но прежде следует отметить, что поскольку область взаимодействия солитонов ограничена, при численном моделировании таких процессов будем считать, что граница среды находится на бесконечности и граничные условия являются естественными: на бесконечности функция W ( t , x ) тождественно равна нулю вместе со всеми своими производными.

Численные эксперименты показали, что взаимодействие однополярных солитонов со скоростями, меньшими 0,77, неустойчиво. При больших скоростях солитоны ведут себя подобно линейным волнам: они сливаются, их суммарная амплитуда возрастает примерно на 15 ^ 20%, затем амплитуда падает и солитоны расходятся, правда, слегка деформированными, что свидетельствует о неупругости их взаимодействия. «Классические» же солитоны, такие как солитоны Кортевега–де Вриза, Шредингера и другие, не сливаются, а только подходят друг к другу на некоторое расстояние, как бы «обмениваются импульсами», и затем расходятся, претерпевая временную задержку (или ускорение), называемую сдвигом фазы, но в итоге «классические» солитоны не изменяются. В нашем случае солитоны также получают временную задержку, однако называть ее сдвигом фазы некорректно, так как при взаимодействии солитоны изменяются, к ним «примешиваются» квазигармонические волны, движущиеся со скоростью, близкой к 1. Но точно определить продолжительность взаимодействия не представляется возможным, можно лишь сказать, что она прямо пропорциональна ширине взаимодействующих солитонов.

Столкновение разнополярных солитонов происходит по другому сценарию: их совместная амплитуда падает до нуля, а взаимодействие устойчиво, уже начиная со скоростей v ^* (см. Рис. 4). Так как амплитуда взаимодействующих солитонов падает, то скорость их движения увеличивается, поэтому уменьшается время взаимодействия. Полагая, что солитоны, находящиеся на расстоянии 10 А , где А — ширина солитона, не влияют друг на друга, предлагаем для оценки «коэффициента искажения времени» формулу:

Kt = ( Тэ - Тт )/То

где T _Э — время взаимодействия, полученное в эксперименте, T _т — теоретическое время прохождения солитоном расстояния 10 А без взаимодействия, Т_о — время прохождения солитоном своей ширины.

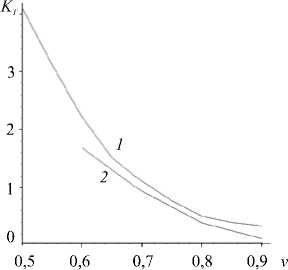
Рис. 5. Зависимость «коэффициента искажения времени» K _T от скорости взаимодействующих солитонов при различных значениях c ² : 1 (кривая 1 ); 4 ( 2 )

На рисунке 5 показана зависимость коэффициента K _T от скорости взаимодействующих солитонов при различных c ² . Из рисунка видно, что при скоростях, близких к 1, «коэффициент искажения времени» стремится к нулю, то есть солитоны вырождаются в линейные волны.

Процесс столкновения разнополярных солитонов показан на рисунке 6. В начальном состоянии солитоны находятся на расстоянии 10 А и не влияют друг на друга (Рис. 6, а ). Далее, после столкновения, они опять расходятся на 10 А . Видно, что после столкновения солитоны практически полностью восстанавливаются, за исключением небольшого участка с деформацией (заключенного на рисунке в овал), которая является пакетом квазигармонических волн, движущихся со звуковой скоростью. Через некоторое время солитон «очищается», то есть отстает от волнового пакета

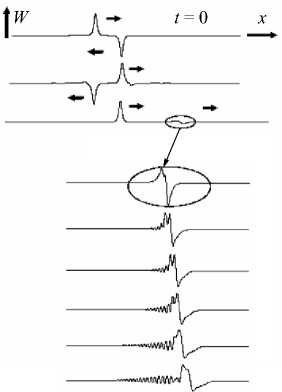
а

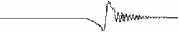
б

Рис. 6. Столкновение разнополярных солитонов: c ² = 1 ( а ); c ²’ >  1 ( б )

и движется в соответствии со своими характеристиками, незначительно изменившимися в результате взаимодействия. Ниже на этом же рисунке в увеличенном масштабе показана эволюция волнового пакета. Рисунок 6, а соответствует c ² = 1, когда формально дисперсия в линейном приближении отсутствует. Однако видно, что низкочастотное возмущение имеет большую скорость, чем высокочастотное. Это свидетельствует о наличии в системе нелинейной дисперсии. Если после «очищения» солитона «выключить» нелинейность, то волновой пакет будет двигаться без изменения формы весьма длительное время, вследствие чего напрашивается вывод, что дисперсия из-за дискретности расчетной схемы, как минимум, на порядок меньше нелинейной.

На рисунке 6, б показан тот же процесс столкновения разнополярных солитонов при c ² >  1, когда присутствует дисперсия линейных волн. Процесс практически не отличается от предыдущего, за исключением эволюции квазилинейного пакета. Теперь уже высокочастотные составляющие имеют большую скорость по сравнению с низкочастотными, и распространение квазигармонических волн происходит как бы в зеркальном отражении.

7.    Сверхзвуковые солитоны

Сверхзвуковые солитоны, распространяющиеся со скоростью v >  c ² , описываются теми же формулами (15) или (18), где амплитуда по-прежнему A = ^б|1 - v ²| . В этом случае энергия является монотонно возрастающей функцией скорости, и солитоны устойчивы при любых скоростях, поэтому здесь можно рассматривать различные виды взаимодействий (и «догонное», и встречное) однополярных и разнополярных солитонов. С точки зрения удобства графического представления результатов целесообразно исследовать «догонное» взаимодействие однополярных солитонов. Качественно различные сценарии «догонного» взаимодействия зависят не столько от энергии взаимодействующих солитонов, сколько от относительной скорости столкновения.

При небольшой относительной скорости столкновение происходит аналогично сценарию обменного взаимодействия классических солитонов. Солитон с большей скоростью догоняет солитон с меньшей скоростью, они сближаются на некоторое расстояние, не сливаясь. Затем амплитуда медленного солитона возрастает, а быстрого — падает; происходит, по сути, обмен энергией, после чего солитоны расходятся, продолжая движение в соответствии со своими скоростями, как показано на рисунке 7, а . Создается впечатление, что солитоны взаимодействуют упруго, так как после столкновения изменения характеристик солитонов не наблюдается.

При большей скорости движения солитоны проходят сквозь друг друга как прозрачные, при этом амплитуда суммарного возмущения не возрастает. В результате столкновения солитоны теряют относительно небольшое количество энергии. Ее потери реализуются в пакет квазигармонических волн, как показано на рисунке 7, б . Интересно отметить, что волновой пакет распространяется в противоположную сторону, то есть если взаимодействующие солитоны движутся слева направо, то пакет движется справа налево.

Дальнейшее увеличение скорости взаимодействия приводит к тому, что образуются два пакета квазигармонических волн, причем один из них, как и на рисунке 7, б , движется в противоположную сторону, а другой в ту же сторону, что и солитоны (Рис. 7, в ). Пакет квазигармонических волн показан на рисунке 8, а в увеличенном масштабе. Его дальнейшая эволюция подобна той, что демонстрирует рисунок 6, б . Попутный пакет изображен на рисунке 8, б .

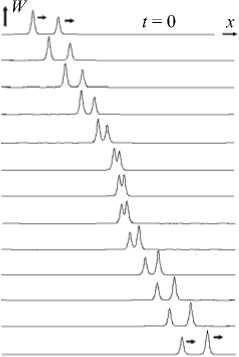
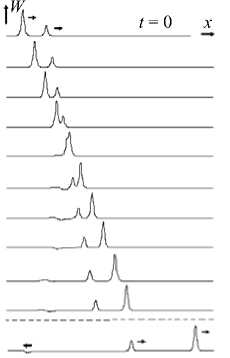
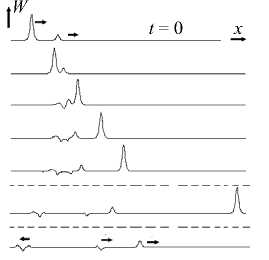
в

Рис. 7. Попутное взаимодействие сверхзвуковых солитонов при скорости столкновения v c <  1 ( а ), 1 <  v c <  1,5 ( б )

и 1,5 <  v c <  2 ( в )

Взаимодействия солитонов, приведенные на рисунке 7, получены при относительных скоростях столкновения 0,8, 1,2 и 1,8 соответственно. Сравнительно большие скорости столкновения солитонов, приводящие к расщеплению, удобнее исследовать, когда солитоны движутся навстречу друг другу (встречное взаимодействие). Из соображений симметрии взаимодействующие солитоны должны быть одинаковыми.

а б

Рис. 8. Пакет квазигармонических волн ( а ) и попутный пакет ( б ) в увеличенном масштабе

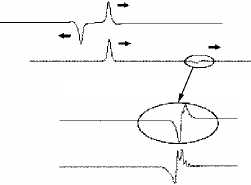
Наиболее эффектно выглядит процесс расщепления при встречном движении разнополярных солитонов (Рис. 9, а ). Под расщеплением понимается такой эффект, когда два солитона с начальными амплитудами A после взаимодействия образуют большее количество вторичных солитонов с амплитудами A i ( i >  1). На рисунке 9, а показано образование двух вторичных солитонов и, естественно, нестационарного волнового процесса. По отношению к начальной амплитуде A ₀ амплитуды вторичных солитонов распределяются следующим образом: A 1 = 0,96 A 0 , A ₂ = 0,27 A 0 (относительная точность измерения составляет 1,2%). Интересно отметить, что такое распределение амплитуд вторичных солитонов не зависит от значения параметра c ² в диапазоне 1 <  c ² <  5 и от относительной скорости взаимодействия в диапазоне 5 <  v c <  16 .

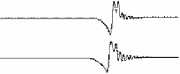
Расщепление при «догонном» столкновении в едином масштабе продемонстрировать невозможно, так как скорости вторичных солитонов различаются почти на порядок, а их амплитуды — практически на два порядка. Поэтому на рисунке 9, б , полученном при c ² = 64/25 и скоростях солитонов большого v = 20 и малого v = 5, показаны только отдельные фрагменты взаимодействия, причем некоторые из них в увеличенном масштабе. После того как более скоростной солитон опережает более медленный и оба солитона «очистятся», на месте взаимодействия остается нестационарный волновой пакет, из которого выделяются еще два разнополярных вторичных солитона (см. уровень I и солитоны в увеличенном масштабе). После выделения этих вторичных солитонов остается квазигармонический волновой пакет (см. уровень II и ниже он же в увеличенном масштабе).

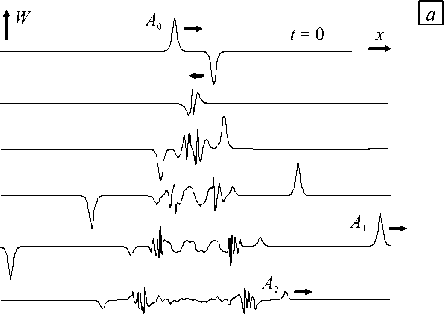
Рис. 9. Расщепление разнополярных солитонов при встречном взаимодействии ( а ) и однополярных солитонов при попутном взаимодействии ( б )

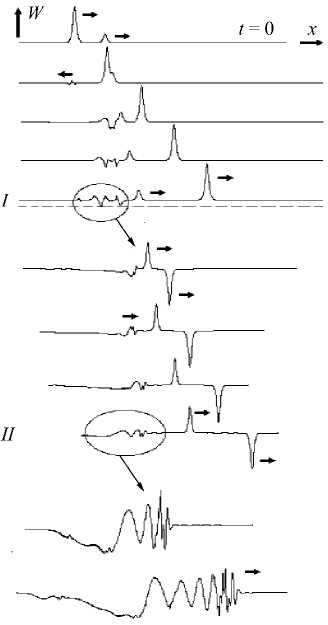
8.    Заключение

В данной работе проведено численное исследование встречного и попутного взаимодействий сильно нелинейных солитоноподобных дозвуковых и сверхзвуковых волн в одномерной зернистой среде, моделируемой неинтегрируемой системой нелинейных уравнений в частных производных. В зависимости от значений параметров микроструктуры система может обладать как жесткой, так и мягкой нелинейностью.

В системе с мягкой нелинейностью могут существовать дозвуковые солитоноподобные волны, которые устойчиво распространяются, начиная с некоторой скорости. Дозвуковые солитоны воздействуют друг на друга неупруго, при этом наблюдается их взаимное ускорение, то есть отрицательный сдвиг фазы.

В системе с жесткой нелинейностью реализуются сверхзвуковые солитоноподобные волны, которые также взаимодействуют неупруго, однако сценарий взаимодействия зависит от относительной скорости столкновения. При малой скорости столкновения взаимодействие носит обменный характер. При попутном столкновении со сверхзвуковой скоростью могут образоваться один или два пакета квазигармонических волн, распространяющихся в противоположные стороны. Если скорость столкновения превосходит в несколько раз скорость звука, то и при встречном, и при попутном движениях наблюдается расщепление солитона на ряд вторичных солитонов с образованием пакетов квазигармонических волн.

Работа выполнена при финансовой поддержке РФФИ (проекты № 12-08-00888-а, № 12-08-90032-бел_а).