Информационная оптимизация процессов проектирования трубобетонных конструкций с совместным применением стержневых и твердотельных моделей

Acknowledgements. This work was supported by the Russian Science Foundation, project no. 22-13-20009,

На сегодняшний день внедрение современных информационных технологий в производственный процесс – это явление, затрагивающее самые разнообразные экономические отрасли страны [1–6]. Многообразие применяемых конструктивных систем, непрерывное усложнение принимаемых архитектурных решений, перекрестное вовлечение в процесс проектирования специалистов различных научных и производственных сфер – лишь малая часть причин, по которым неотвратима стала и цифровизация современного строительства. С этим связано непрерывное развитие технологий информационного моделирования строительных объектов (ТИМ), усовершенствование существующих методик расчета конструкций с использованием продвинутого программного обеспечения.

Эпоха отвлеченного от компьютерной науки развития строительной области осталась в прошлом, в настоящее время любая идущая в ногу со временем проектная организация непрерывно ощущает потребность в накоплении своих информационно-технических ресурсов, оптимизации и рационализации их использования.

Однако некоторые задачи, возникающие в процессе проектирования, при традиционном прямолинейном их решении с использованием даже самого технологичного компьютера, настолько сложны, что могут привести к полному истощению мощностей вычислительной техники и нехватке ее производительности. Одной из таких задач является расчет строительных конструкций с применением композитных материалов [7–9], например, сталежелезобетонных или, в частности, наиболее распространенных на сегодняшний день – трубобетонных [10–18].

Возникающие в процессе расчета сложности [13, 18] объясняются особыми свойствами, приобретаемыми конструкциями вследствие совместной работы двух различных по физико-химическим показателям материалов – стали и бетона [14–17]. Как и для любого композитного материала, одной из главных целей статического расчета таких конструктивных элементов является получение картины распределения напряжений в их сечениях, позволяющей произвести оценку прочностных и жесткостных характеристик каждого элемента в отдельности и всей конструктивной системы в целом [18].

Для достижения заданной цели возможно применение двух различных подходов к моделированию расчетных схем композитных стержней. Пер- вый предполагает максимально возможное упрощение конструктивного элемента до элементарной стержневой модели, геометрические и физические характеристики которой задаются как цифровые значения, а сама модель может состоять в наиболее простых случаях из одного конечного элемента, имеющего единственную визуализируемую в расчетной схеме характеристику – длину рассматриваемого стержня. Второй подход предполагает создание твердотельной конечно-элементной модели, учитывающей действительные габариты поперечного сечения стержня. В этом случае физические свойства материалов его компонентов присваиваются каждому конечному элементу модели, количество которых может изменяться в зависимости от требуемой в расчете степени точности.

На рис. 1 приводится схема, обобщающая преимущества и недостатки стержневых и твердотельных расчетных моделей композитных стержней.

В статье описывается методика расчета трубобетонных конструкций, следование которой позволяет минимизировать потребную производительность вычислительной техники в процессе достижения вышеописанных целей.

Метод

Традиционный подход к статическим расчетам конструктивных схем зданий и сооружений заключается в их рациональном упрощении и обобщении в виде конечно-элементных стержневых и/или пластинчатых расчетных моделей и последующем вычислении напряжений в каждом элементе такой модели [13, 18]. При отсутствии в расчетной схеме сооружения элементов, обладающих свойствами композитных материалов, данные расчетные предпосылки позволяют в короткие сроки достичь приемлемых результатов, не испытывая при этом нужды в повышении мощности вычислительной техники.

Однако использование композитных материалов заставляет отказаться от подобной методики ввиду сложности корректного присвоения стержневым трубобетонным элементам жесткостных характеристик, распределение которых в составе расчетной модели напрямую повлияет на итоговые расчетные усилия.

Невозможность применения стержневых моделей для расчета трубобетонных конструкций может привести к необходимости их моделирования в качестве объемных конечных элементов в составе расчетной схемы. Однако данное решение неизменно приводит к многократному повышению

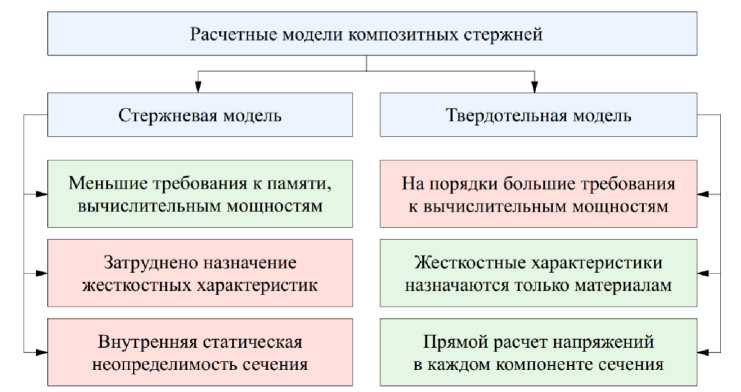
Рис. 1. Преимущества (зеленый) и недостатки (красный) стержневых и твердотельных расчетных моделей композитных конструкций

степени дискретизации расчетной модели, резкому увеличению количества конечных элементов и, как следствие, возрастанию требуемых для расчета временных ресурсов и вычислительных мощностей, при параллельном усложнении процесса моделирования.

Делая вывод о практической непригодности модели, составленной из объемных конечных элементов, необходимо признать невозможным и отказ от стержневой модели зданий и сооружений при их статическом расчете. При этом решением проблемы корректного задания жесткостных ха- рактеристик могут выступать численные исследования, проводимые для отдельных конструктивных элементов, моделируемых дискретно в полном объеме, но не являющихся при этом частью общей стержневой модели конструкции.

Для наглядного представления метода, позволяющего анализировать напряженно-деформированное состояние трубобетонных конструкций с использованием комбинации стержневых и твердотельных конечно-элементных моделей, на рис. 2 показана структура, иллюстрирующая основные этапы выполнения расчета.

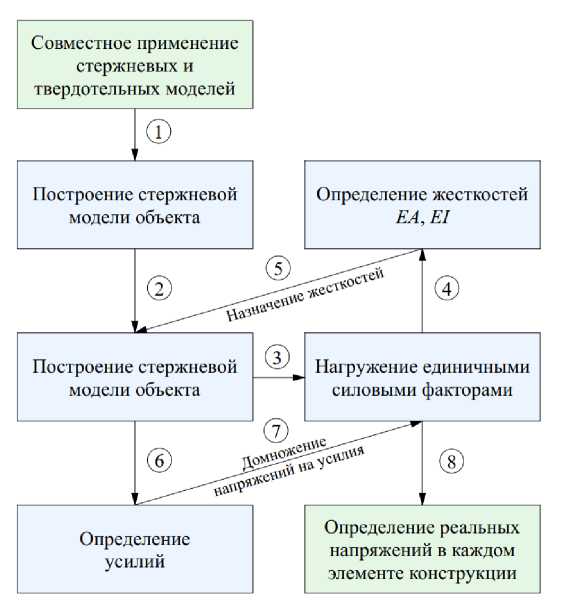
Рис. 2. Структура проведения совместных расчетов с применением стержневых и твердотельных расчетных моделей

В качестве демонстрации предлагаемого под-

хода к определению жесткостных характеристик процесс рассматривается на примере цифровой компьютерной модели трубобетонной колонны (рис. 3), каждому компоненту сечения которой

присваиваются геометрические и жесткостные характеристики, свойственные соответствующему конструкционному материалу. Расчетная схема

колонны при этом упрощается и представляется в виде жестко-защемленной консоли, находящейся под влиянием единичного силового фактора.

Значение перемещения конца стержня Д_А может быть определено по формуле Мора – Максвелла (1) или по правилу Верещагина (2):

Если перемещение точки A является известной величиной, становится возможным решение обратной задачи с целью определения значения эквивалентной жесткости рассматриваемой трубобетонной колонны. Компьютерное моделирование отдельного стержневого элемента (рис. 4б) позволяет произвести его статический расчет и однозначно определить значение Д_А , а затем выделить значение эквивалентной жесткости колонны из формулы (2):

Е]

экв

Ml2

2Дл

1 Hw36 м2 2^0,116 •IO^-7 м

1,55 • 106 кН^м2.

Д_л = fM^ Ss, ^А 0° Е]₃кв

Д_А = М^— ,

^2Е /экв

где I - длина стержня; М_р - ордината на эпюре моментов M p (эпюра на рис. 4а); M_t - ордината на эпюре M i (эпюра на рис. 4а); Е/_экв - искомая жесткость колонны; ds - дифференциал длины стержня.

Таким образом, задача определения изгибной жесткости трубобетонного элемента для задания в пространственную стержневую расчетную модель любой сложности не требует интеграции в модель объемных конечных элементов (со всеми сопутствующими осложнениями процесса расчета) и сводится к ряду исследований с применением компьютерного моделирования отдельных стержней, а точнее – к числу таких исследований, равному

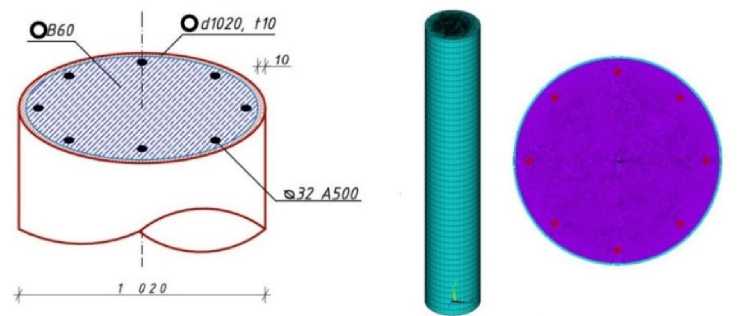
а)

б)

Рис. 3. Компоненты трубобетонной колонны (а) и ее цифровая модель (б)

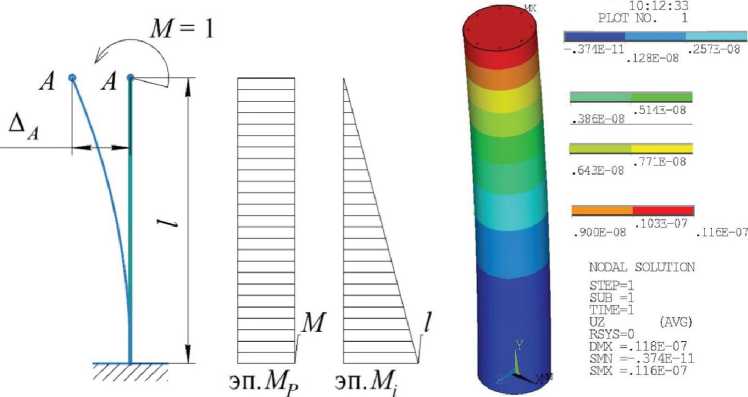
а)                                                   б)

Рис. 4. Упрощенная расчетная схема колонны: а – графическое отражение; б – цифровая модель

количеству типоразмеров применяемых композитных конструктивных элементов (см. рис. 2).

Данный подход с равным успехом может быть применен к определению продольных жесткостей с разницей в том, что единичный момент в расчетной схеме (см. рис. 4а) должен быть заменен единичной продольной силой.

Результаты и обсуждения

В качестве объекта для применения вышеописанного метода в исследовании выступает конструктивная схема, эквивалентная высотному зданию, напряженно-деформированное состояние конструкций которого предлагается оценить с применением его пространственной стержневой конечно-элементной модели (рис. 5) [13, 18].

Колонны представленного в качестве примера объекта представляют собой трубобетонные стержни, изгибные и продольные жесткости которых определялись в соответствии с изложенным алгоритмом по формуле (3) и присваивались каждому соответствующему конечному элементу расчетной модели здания [13, 18], что в конечном итоге позволило произвести корректный статический расчет его модели и выделить наименее выгодные комбинации нагрузок, соответствующих наибольшим расчетным усилиям в исследуемых трубобетонных элементах колонн.

Для колонны, рассматриваемой выше (см. рис. 3а), значения расчетных усилий для двух наименее выгодных комбинаций в составе представленной конечно-элементной модели составили:    Мрасч = 245 кНм, Nрасч = 16 675 кН    и

^ расч = 360 кНм, N_расч = 13 035 кН по критериям N max и M max соответственно.

Накладывая усилия на пространственную твердотельную модель отдельной трубобетонной колонны (см. рис. 4б), возможно проверить прочность ее элементов по формуле

_ расч . расч _

^max = 0 м + ° N =

О м • М расч + O n • N р _a сч <  R y ,                (4)

где о расч, о расч - возникающие в элементе конструкции напряжения от действия расчетных момента или продольной силы (см. рис. 5); о_м, a_N - те же значения, но вызванные единичным силовым фактором (моментом или продольной силой), определяемые по рис. 6 и 7 соответственно; М _расч , N р_асч -расчетные момент и продольная сила, представленные выше; R_y - расчетное сопротивление материала (стали трубы, стали арматуры, бетона),

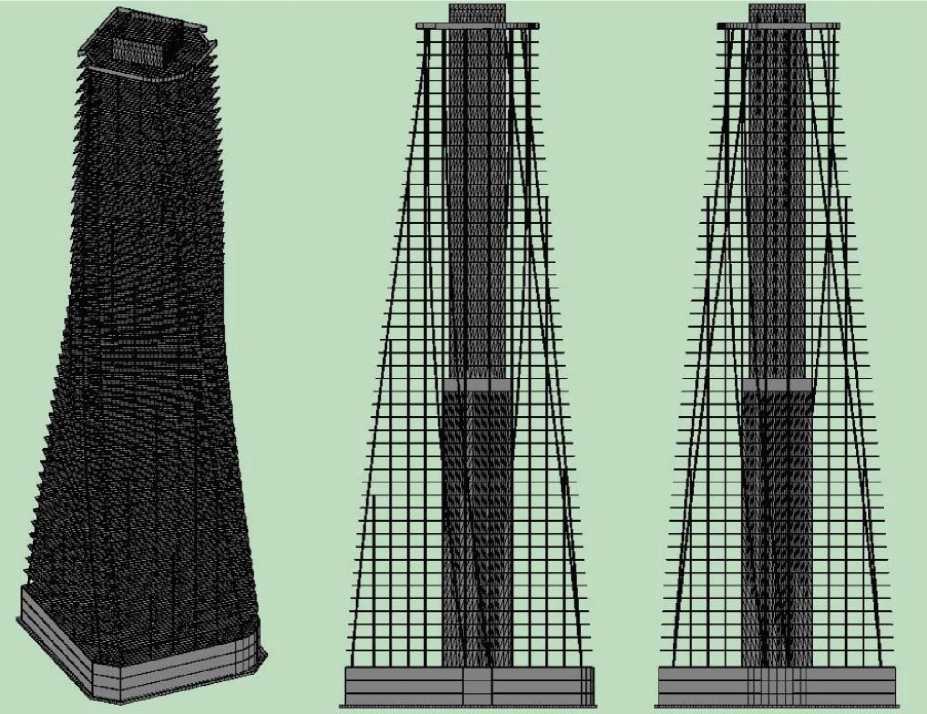
Рис. 5. Пространственная конечно-элементная расчетная модель высотного здания

KCDAL SOLUTION

NODAL SOLUTION

(АТС)

(АТС)

ANSYS

2019 R2

ANSYS

2019 R2

RSYS=O

DMX =.369E-09

SM< =-13.3453

SMX =-.539274

SUB =1

TIME=1

SY

1Л0.501

APR 1 2021 09:38:54

HOT ND. 1

SUB "1

TM-1

SY (АТС)

BSYS=O

ЕМС «.369E-C9 St® - 13.3453 SMC --.539274

ANSYS

2019 U

-26.1672

-2.90286

2.913227

-59-7822

-179.319

APR 09:30:54

33.5046 ^

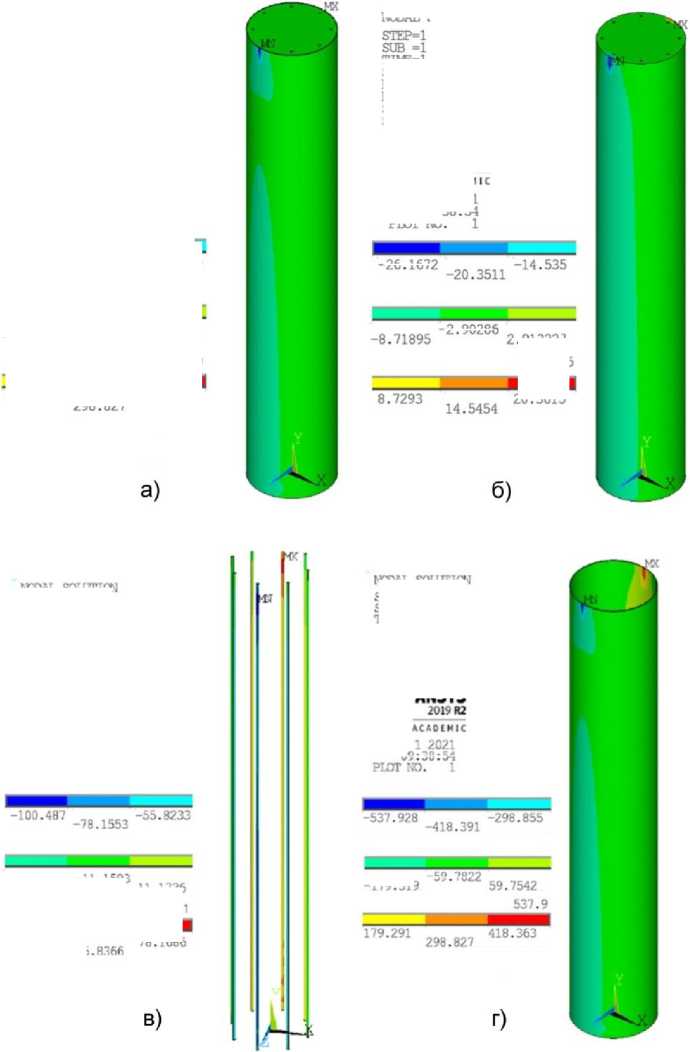
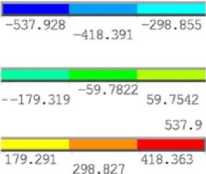
Рис. 6. Нормальные напряжения (Па) в элементах трубобетонной колонны от действия единичного момента: а – композитная конструкция; б – бетон; в – арматурные стержни; г – стальная труба-оболочка

TIME=1 SY

RSYS=O

DMX =.369E-09

SMQ =-1.1671

SMX =-.396243

APR 1 2021 09:38:54 PLOT №.

APR 1 2021 09:38:54 PLOT NO. 1

NODAL SOIOTION

NCDAL SOLUTION

STEP-1

SUB -1

TIMS=1

SY

(AVC)

=SYS3

I»: .369E-C9

S№ —13.3453

ЯК —.5392 74

ANSYS

26.1776

20.3615

-33.4913 * ’ 93 11.1726

78.1686

определяемое по соответствующим нормативным документам.

Результаты расчета прочности трубобетонной колонны (см. рис. 3а) с использованием формулы (4) сведены в таблицу.

Таблица демонстрирует, что описываемый алгоритм расчета трубобетонной колонны позволяет оценить несущую способность каждого компонента ее сечения дискретно, учитывая при этом их совместную работу, что говорит о достижении одной из главных целей статического расчета таких конструктивных элементов.

По результатам выполненного расчета можно заключить, что прочность колонны обеспечена. При этом максимальные запасы прочности возникают в арматурных стержнях, тогда как материал стальной трубы-оболочки работает практически на пределе, что визуализирует диаграмма коэффициентов использования материала различных компонентов колонны (рис. 8).

NODAL SOLUTION

-10.4995

-.539274

a)

-4.80795    „     -1.96217

-3.38506

-9.07663 "7"65374 -6.23084

NODAL SOLUTION

SIEP=1

SUB =1

TI№=1 SY RSYS=O

DMX -.369E-09

SMN =-13.3453

SMX =-.539274

ANSYS

2019 R2

ACADEMIC

APR 1 2021 09:38:54 MOT NO.

SUB =1 TIME-1 SY RSYS=O dmx =.:

(AVG)

369E-09

SMI =-13.3453

SMX —.539274

ANSYS

2019 R2

ACADEMIC

APR 1 2021 09:38:54 PLOT NO. 1

-12.4078    _ -11.336

-11.8719

-10.2642

-10.8001          -9.72827

-7.58463

-9.19236 л -8.12054

-8.65645

B)

«

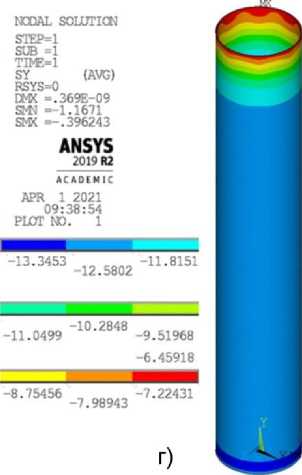
Рис. 7. Нормальные напряжения (Па) в элементах трубобетонной колонны от действия единичной продольной силы: а – композитная конструкция; б – бетон; в – арматурные стержни; г – стальная труба-оболочка

Проверка прочности элементов колонны

Комбинация усилий		Элемент	° M , Па	G n , Па	расч Па • 10 6	расч Па • 10 6	Gmax , Па • 10 6	Ry , Па • 10 6	Запас, %
М расч, Нм	N расч , кН
245000	1,668^ 10 6	Бетон	20,36	1,16	4,99	19,3	24,3	33,0	26
		Арматура	78,17	12,41	19,2	207	226,2	436	48
		Труба	179,32	12,58	43,9	210	253	265	5
360000	1,304-10 6	Бетон	20,36	1,16	7,33	15,1	22,8	33,0	31
		Арматура	78,17	12,41	28,1	162	190,1	436	56
		Труба	179,32	12,58	64,6	164	228,6	265	14

Коэффициент использования

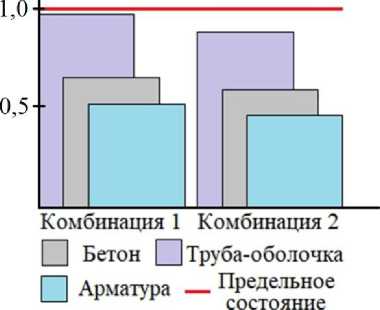
Рис. 8. Диаграмма коэффициентов использования компонентов трубобетонной колонны

Коэффициент включения в работу различных составляющих композитного сечения позволяет судить о необходимости внесения корректировок в конструкцию для создания наиболее экономичного сочетания материалов.

Выводы

Комбинированный подход, предполагающий использование как общей стержневой, так и объемной конечно-элементных моделей, позволяет произвести проверку прочности каждого конструктивного элемента трубобетонной колонны независимо друг от друга, не пренебрегая при этом учетом совместности их работы. При этом необходимые усложнения процесса компьютерного моделирования сводятся к приемлемому минимуму и сопряжены только с созданием отдельных простейших конечно-элементных моделей трубобетонных стержней и их расчетом.

Дискретный расчет каждого используемого типоразмера композитных элементов ведет к уменьшению потребных вычислительных мощностей в сравнении с методиками, предполагающими непосредственное внедрение объемных элементов в пространственную стержневую расчетную модель.

Поэтапный характер проведения таких расчетов при этом способствует ускорению процесса проектирования и его рационализации с точки зрения планирования и грамотного тайм-менеджмента. Уменьшается при этом и цена субъективной ошибки проектировщика при задании жесткостных характеристик и моделировании. Это связано с тем, что повторное проведение расчета, признанного некорректным, применительно к простой расчетной модели займет кратно меньше времени, чем перерасчет «тяжелых» пространственных твердотельных моделей, сопряженный с высокой степенью задействования информационно-технических ресурсов.

Более того, выбранный расчетный алгоритм позволяет производить корректировку и оптимизацию сечений по коэффициентам использования материала с использованием твердотельной конечно-элементной модели, производя все изменения в составе сечения без задействования общей стержневой модели, лишь заменяя в ней значения эквивалентных жесткостей. Данный аспект также можно рассматривать как преимущество подхода, предполагающего наличие этапа компьютерного моделирования отдельных элементов при проектировании конструкций из композитных материалов, таких как трубобетон.