Information training technology: learner’s memory state model

доступа: Загл. с экрана.

The training process is one of the oldest ones in the world. Everybody played the role of learner and teacher, and everyone knows that it is rather difficult in both cases. For the problem of training foreign language we consider it is of greater importance. In contrast to other fields the process of training foreign language is based on the properties of human memory which is different amongst people.

The information computer systems are the main tool of modern training technique. This choice is absolutely clear: as a matter of fact the training process is a transfer of information, and information searching systems should do it. But it is one of possible approaches to training as information process. There exist fields where it is very effective, but this approach should not be considered training process, information portion, training algorithm.

absolutely right, because it does not try to individualize the training process.

In recent years another approach is developed when training can be considered as control [1]. The relations between teacher and learner can be interpreted as relations between the control object and the control device. This approach allows to use the methods of control theory. For effective training it is necessary to have a trainer model. Surely it is an approximated model and we should adapt its parameters and structure to provide its adequacy to real object.

This approach is rather advanced for the problem of training foreign language because the trainer capability to master lexical units is connected with his (her) memory [2].

We modified the approach of professor L. A. Rastrigin in order to solve this problem in a multilingual sense. We will take a result of psychological memory research as a trainer model, namely exponential dependency of ignorance probability of a lexical unit upon forgetting rate and time. Further we are going to consider it in detail.

Training as control. The standard training problem usually consists in that a learner should memorize determined information portions, and this problem can be formulated as the control problem.

In this case the learner is an object of control, and a teacher or trained device is a source of control. Obviously, this is a complex object and we can use all known principles of control by a complex object [1].

Look at the training process scheme (fig. 1). The control object is an object of training (called a “trainer”), the control device is a trained unit (called a “teacher”). Y is a trainer’s state, measured by data unit D y ; Y - information about trainer‘s state got by a teacher in answer to questions U , besides U includes the portions of training information. Purposes of training Z ^* and resources R are given to the teacher.

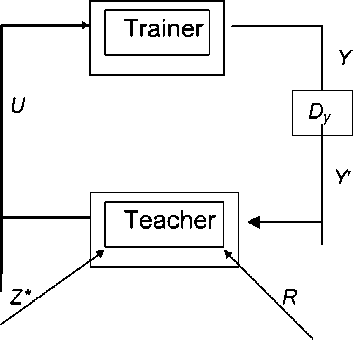
Fig. 1. Training process scheme

The problem is to organize the training U , changing trainer‘s state Y to achieve the formulated purposes Z ^*:

U = ф Y , Z , R ), where ф is an algorithm of training.

As a rule the training process in computer training systems is realized in the next way. A trainer gets an information portion, which should be learnt. Then he is tested to determine a level of training quality. Answers of the trainer are checked and he gets the new information portion. The information portion sequence is determined by the training program [3]. The linear and branched training programs are widely spread. Besides the branched programs are divided in two types: outer and inner regulating ones.

New statement of the training problem. We should formulate new statements of the training problem [4]. We formalize:

• –    training purpose Z ^*;

• –    training information ;

• –    trainer model;

• –    algorithm of training .

We present the training process as sequence of seances (lessons) beginning at time moments t ₀, t ₁, ..., t_n . To determine the effectiveness we take a function of training quality Q_n = Q ( Y_n ), where Y_n – state of object at moment t_n . The purpose is to minimize Q by training:

Q ( Y ) ^ mn-

Since a level of absolute training Q^* can not be achieved because of real properties of the human memory the training process should be terminated, when the criterion of quality reaches some given quantity 5 :

Q n ^s ,

• w here 5 >  Q* is quantity, close to Q * .

Purpose Z^* can be formalized as

Z . | Q ( Y * ) ^5, ’ [ T ( Y *) = min, where T ( Y^* ) – time, necessary to reach the state Y^* .

We formalize training information (TI). We consider such process, where TI can be presented as a finite state of enumerated elementary portions: U = {1, 2, ..., N }. At every seance with help of the training algorithm the following subset is constructed:

U n = { ^u i , ^u 2 ,..., ^um„ } U * u j пРи i * j , ^U i ^{e U} .

This subset contains M_n elementary portions of TI with the corresponding numbers.

We consider the trainer model. We describe a trainer state at the n -th seance by an ignorance probability vector:

Yn = Pn = (p1n, p2n, ..., pNn), where pin – ignorance probability of the i-th element at moment tn.

Using data of psychology in the field of memory research we choose exponential dependency as a model:

Pn = Pi(tn) = 1 - e -ann , where ain – rate of forgetting the i-th element at the n-th seance; tin – time after last learning the i-th TI element. The forgetting rate of each element is reduced, if this element is given to the trainer to learn, and it is not changed otherwise:

• a n ,if i 6 U n ,

• Y ' a n , if i e U n and r n = 0,

• Y " a n , if i e U n and r n = 1, n = 1,2,...,

  a ^{n +1} = ‘

  
  

where Y‘ , Y", a i ¹ ( i = 1, 2, ..., N) - parameters defining the individual features of trainer memory; 0 <  y' <  Y" < 1, a'> 0.

Answers to tests can be written as:

• 0, if answer is right, _r ⁿ = < ‘     [ 1, otherwise.

The effectiveness criterion Q should define a level of training. For the foreign language learning problem the level of training is defined by ignorance probability of any TI element:

N

Qn =ZPi(tn)9,max -U^min fi Un, where 0 < qi < 1 is a frequency of the element appearance in the given text, Sqi = 1; qimax = max q {qi1, qi2, qi3}, qi1, qi2, qi3 – frequencies of English, German and Russian word from the corresponding multilingual frequency dictionary [5].

A result of the problem solution is an optimal TI portion U_n ^* given at the n -th seance.

To minimize Q_n it is necessary to include the elements of the greatest meaning of multiplication p_i ( t_iⁿ ) q_i in U_n ^* because their memorizing causes multiplication vanishing and decreases the meaning Q_n essentially.

Therefore it is required to find M_n maximal members of sum in the criterion, whose indexes define TI portion. They can be found by the rule:

u 1 = arg maxpi(ti)q™, u2 = arg max p, (tn)q,max,

• ²           1< i <  N , i * N

....                           (1)

um„ = argmaxpX ti) q.-mx, i * Uj (j = 1, 2,-, Mn -1), where arg max {a} = i * is index i * e U of maximal a,, it means ai* = max ai, and {u1, ..., uMn} = U* – TI portion given to the trainer at the n-th seance.

Let T_n be the duration of the n -th seance or time for learning the portion. We assume that time of learning the i -th element is directly proportional to its ignorance probability. Then

^M n = max 1 ^M : ^T n ^{- K} E   P i⁽ t i ) >  ’

1< M < N                       ,.

l                          Ie{u,,...,UM}

i e {

where к - average learning time of TI element at its first presentation to the trainer; u ₁, ..., u_M – numbers of TI elements. Parameter к is unknown a priori and should be adapted:

к*+1 =K* + v (T"- T„),(3)

where v is unmeasured coefficient of adaptation rate, T_n is time spent by the trainer to learn U_n .

Training Algorithm. Thus the training algorithm [6] can be can be presented in the following way.

• 1.    Check knowledge of portion U_n and construct the set R_n .

• 2.    Realize parameter adaptation:

• 3.    Correct the ignorance probability vector, i. e. form P_{n +1} according to our exponential dependency, using previous rule and taking into account forgetting time of information after last learning t_iⁿ :

• 4.    Calculate Q_{n +1}.

• 5.    If Q_{n +1} < 3 then the training process is terminated; otherwise you should define portion U_{n + 1} by (1), and present this portion to the learner taking into account rules (2) and (3). The points 1...5 are repeated again and so on.

a i ,if i t Un, a n +1 = Jy ‘ a", if i e U and rn = 0, i     ini

Y " a n , if i e U_n and r n = 1, n = 1, 2,...,

,    [ At , if i e U , tn+1 = J    n ,             n

‘ " [ t n +A t_n ,if i t U_n , n = 0,1,....

Model Parameter Estimate. When exploring the trainer model the problem of estimate of unknown parameters is appeared. We should estimate parameters of correction of forgetting rates y' and y" and initial meaning of these rates a ¹ = ( a , ¹, ..., a _N ¹). These parameters describe individual features of the trainer memory.

a ¹ can be estimated by maximal likelihood method. We can show it [3]. The likelihoodfunction is constructed:

P = px(1 – p)Kn–x, where x = ^ r" is a number of elements unremembered i eU„ from Kn. The set Un = {u1, …, uKn} contains the elements given to the trainer for the first time. Changing P for lnP, we have d ln P da

xe a t t

1 - e a '

+ ( x - K n ) t = 0.

We get an estimate of parameter a :

^K n ^{- x}

.

)1

a = —ln t

K n

Parameters y' and y'' can be also estimated by maximal likelihood method [3]. Before training we should have experimental data presented by the set R_n . The trainer gets N strange words to memorize. Then he is tested, the required set R_n contains the test results. The trainer should learn the unremembered words until r_iⁿ = 0 for all i = 1, 2, …, N .

The data obtained with help of this experiment can be described by our model. In this case M_n = N and A t_n = 1 for all n = 0, 1, …, K , where K – number of tests, i. e.

I N

K = min <  n : ^r. = 0 l tr

The forgetting rates are changed

Jy ' a", if rn = 0, a n+1 = J

'       Iy"an, ifrn = 1, where 0 < y' < Y" < 1, i = 1, 2, ., N, n = 1, 2, ., K. The ignorance probabilities have the following form:

p n = 1 - e-a n ,i■ = 1, 2,..., N , n = 1, 2,..., K .

It is taken into account here that all the words ( M_n = N ) are learned everyday ( A t_n = 1).

Let An be the set of word numbers unremembered before the n-th test; Sn - amount of these words, I An I = Sn. Then for all i e An we have an = (Y")n-1 a, p" = 1 - e - n = 1 - e- *-1a= pn, n = 1,2,....

The experimental data can be presented by the set R_n of realizations r n of variates ^ in with the following distribution:

P { ^ ⁿ = 1} = p n ;

P { ^ ⁿ = 0} = 1 p n , I = 1,2, ., N .

We denote xn =E (1 - rn), ie An and construct the likelihood function

P = n pS" -xn (1 - p* ) xn = n=1

= Г! [1 - e ^{- ( Y} ' ) " - ’ “ ] S n - ^x " [ e ^{- ( Y} ) " - ’ “ ] x_n .

n =1

We change P for ln P and take a partial derivative over y' ' in order to find a maximal meaning ln P :

д ln P dy"

K

= 2

n =2

Sn  \ e n - 1 a ( n — 1) x

П — I

1     o ^—(Y ) ^a

1 — e

. x( y " ) ⁿ 2 a — x n ( n — 1)( y " ) ⁿ 2

= 0.

We get an equation for finding y" "

K

2 — n---n   e -(^y ) ^a ( n — i)(y " )

² 1 — e ~⁽y") n ^a

K

= 2 X n ( n — 1)( Y 0 ^{n — 2}.

n =2

Obviously, it is impossible to get an exact solution of this equation, ifK >6. Therefore, we should simplify it.

We change e-

2 (Sn — Xn)(n — 1) = «2 Sn (n — 1)(у") n^—1. n=2                             n=2

First of all we construct an approximated solution of this equation. In case when the meaning y"" is close to 1, we can use Taylor’s row expansion:

(y"")ⁿ = [НИ'")]n = 1-n(И'") +^.

Applying this expansion we get

K

2 (Sn — Xn)(n — 1) « n=2

K

»a2 Sn (n —1)[1 — (n —1)(1 — y")].

n=2

Now we can estimate y"":

2 [ Sn (a — 1) + Xn ](n — 1) y " = 1 — ^--------------- a2 Sn (n —1)2

n=2

If y" " is strongly different from the unit, this formula should be used for the first approximation to estimate.

For estimating the y" parameter it is necessary to find an average number 0 of times when the words were not memorized and its mathematical expectation M0. 0 can be calculated by experimental data:

KN

0=N 2 2 r:-

The mathematical expectation can be presented following way:

KNKN

M0=22 M^n = 22 Mpi

N n=1 i =1            N n=1 i=1

Since pn = 1 — e~^an « aⁿ, then

KN

M 0« —^ 2M an.

N1=1

in the

Using the elements of probability theory and the method of mathematical induction we get the following expression (the k-th moment of the forgetting rate):

M (an) k = (y") ^kM (an^—1)^k +

+[(y") k — (y") k ] M (an^—1) k⁺¹.

According to this formula all the moments can be calculated. Further we can find Man and MQ.

Maⁿ⁺¹= M{y"ane"^an +y"an (1 — e"^an)} «

«y "Man + (y" — y") M (an )2.

The estimate of y" can be obtained from equality M « 0 and by construction of successive approximations, supposing that Ma.¹ = ai¹ (i = 1,2,..., N). The approximations should be constructed until n = k. Then we get y K_—1 and take it as a parameter y" estimate.

This approach essentially differs from usual training systems that as a matter of fact simulate behavior of a teacher along with his didactic godsends and failures. Suggested approach reduces an influence of a teacher and teaches a trainer, taking into account the individual features of memory. At every step it minimizes a distance between a learner’s state and given purpose. It means that the training is optimal at every step, but it does not guarantee optimality of whole training process. We only get a solution close to optimal.

We took one of the approaches to intellectual technologies synthesis in training, developing new methods of training, proposed by professor L. A. Rastrigin [1]. It considers training process as the learner’s memory state. But one should notice that this method is oriented for the properties of the concrete subject sphere vocabulary, i. e. is based on the multilingual frequency dictionaries.