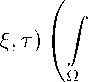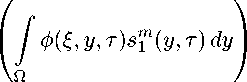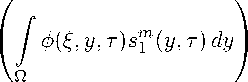Initial Boundary Value Problem for a System of Semilinear Parabolic Equations with Absorption and Nonlinear Nonlocal Boundary Conditions

In this paper we consider the initial boundary value problem for a system of semilinear parabolic equations with absorption and nonlinear nonlocal boundary conditions:

u t = A u + v p — aur, v t = A v + u q — bv s ,	x G Q , t >  0 ,
dv ) = f ф(x, y ,t)u m ( y,t ) dy,	x G d Q , t >  0 ,
Q dV ) = f ^ ( x,y,t ) v n ( y,t ) dy, Q	x G d Q , t >  0 ,	(1)
u ( x, 0) = U o ( x ) ,   v ( x, 0) = V o ( x ) ,	x G Q ,

• ^# This work is supported by the state program of fundamental research of Belarus (project № 1.2.02.2) and the Belarusian foundation for fundamental research within the framework of the project “Systems of semilinear parabolic equations with absorption” (state registration № 20231262).

(0 2025 Bulyno, D. A., Gladkov, A. L. and Nikitin, A. I.

where a , b , p , r , q , s , m , n are positive numbers, Q is a bounded domain in R N for N ^ 1 with smooth boundary d Q , v is the unit outward normal vector on d Q .

Throughout this paper we suppose the following conditions:

ф ( x, y, t ) G C ( d Q x Q x [0 , + ro )) ,    ф ( x, y, t ) ^ 0;

^ ( x, y, t ) G C ( d Q x Q x [0 , + ro )) ,   ^ ( x, y, t ) ^ 0;

u o ( x ) G C 1 (Q) , v o ( x ) G C 1 (Q) , u o ( x ) ^ 0 , v o ( x ) ^ 0 in Q;

^dudV^{x )} = У ^ф(x, y ^{, 0)} u ^{m (} y) dy,    ^dvdV^{x )} = / ^ ^{( х,}У’ ^{0) v} n ⁽ y ) dy ^{on d Q} .

ΩΩ

Let Q t = Q x (0 ,T ) , S t = d Q x (0 ,T ) , Г т = S t U Q x { 0 } , T> 0 .

Definition 1. We say that a pair of nonnegative functions (u(x, t),v(x, t)) is a subsolution of (1) in QT, if u,v G C2,1(QT) П C 1,0(QT U Гт) and ut C Au + vp — aur, vt C Av + uq - bvs dudv— C f ф(x, y, t) um(y, t) dy, Ω

( x,t ) G Q t , ( x,t) G S t ,

(x,t) G St, x G Q,

^dv_d— C f ^ ( x,y,t ) v ⁿ ( y,t dy, Ω

u(x, 0) C uo(x), v(x, 0) C vo(x), a pair of nonnegative functions (u(x, t), v(x, t)) is a supersolution of (1) in Qt, if u,v G C2,1 (Qt) ПC1,0(QtUГт) and it satisfies (2) in the reverse order. We say that (u(x, t), v(x, t)) is a solution of problem (1) in Qt if (u(x, t),v(x, t)) is both a subsolution and a supersolution of (1) in QT.

Definition 2. We say that a solution ( u _max ( x, t ) , v _max ( x, t )) of (1) in Q t is a maximal solution if for any other solution ( u ( x,t ) ,v ( x,t )) of (1) in Q t the inequalities u ( x,t ) C u _max ( x,t ) , v ( x,t ) C v _max ( x,t ) are satisfied for ( x,t ) G Q _T .

A lot of articles have been devoted to the investigation of initial boundary value problems for parabolic equations and systems with nonlocal boundary conditions (see, for example, [1-22] and the references therein). In particular, the problem (1) with a = b = 0 was considered in [11]. Initial boundary value problem (1) with a = b = 0 and Dirichlet nonlocal boundary conditions was studied in [5]. The authors of [23] investigated the existence of global solutions for (1) with zero Dirichlet boundary condition. Blow-up problem for (1) with nonlinear local Neumann boundary conditions was investigated in [24, 25].

This paper is organized as follows. In the next section we prove the existence of a local solution. A comparison principle and the uniqueness of solutions of (1) are established in Section 3.

2.    Local Existence

Let { e j } be decreasing to 0 sequence such that 0 <  E j <  1 , l G N . For £ = £ i let u o _£ ( x ) and v o _£ ( x ) be the functions with the following properties:

U 0 _£ ( x ) ,V 0 _£ ( x ) G C 1 (Q) , U 0 _£ ( x ) >  E, V 0 _£ ( x ) >  E ;

U 0 _£ i ( x ) >  U 0 j , V 0 _£ i ( x ) >  V 0 _{£ j} for E i > E j ;

0 C u o _e ( x ) — u o ( x ) С 2e,   0 <  v o _e ( x ) — v o ( x ) C 2e;

dU Qs ( x )       f          _n \ m \ ,       d v'O_£( x )      / i            n i

--dV-- = J ^Ф(x, У ^{, 0) u}^ ⁽ y ) dy, --dV-- = J ^ ^(x, y, ^{0) v} O e ⁽ y ) dy for ^{x 6 d Q} - Q                              Q

Since the nonlinearities in (1), the Lipschitz condition may not be satisfied, and thus we need to consider the following auxiliary problem:

ut = Au + vp — aur + aEr, vt = Av + uq — bvs + bEs, x∈ x∈ Q, t> 0, Q, t> 0, dVt = f ф(x, У, t)um (У, t) dy, Q x∈ dQ, t> 0,               (3) ddv’ ) = f ^(x,y,t)vn (y,t) dy, Q x∈ dQ, t > 0, Ulxc, 0) = UOe(x), v(x, 0) = VOe(x), x∈ Q, where e = Ei- The notion of a solution (u£,v£) for problem (3) in Qt can be defined in a similar way as in Definition 1.

Theorem 1. Problem (3) has a unique solution in Q T for small values of T.

• <1 We start the proof with the construction of a subsolution and a supersolution of (3)

in Q t for some T . Let sup Q u o _e ( x ) C M , sup Q v o e ( x ) C M, where M ^ 1 . Denote

K = max

sup ^ф(x,y^,t)^, \ Q Qx Q t

sup

Q Qx Q t

^ ^(x, y ^,t)

)

and introduce an auxiliary function ^ ( x ) with the following properties:

^ ( x ) 6 C ² (Q) ,

inf ^(x) > 1 inf d^(x) > К [ max (^m(y), Pn(y)} dy, Q            dQ dVJ

Q where К = К max (Mm 1 ,Mn 1) max (1, exp(m — 1), exp(n — 1)). Let а, в be positive constants such that aq — в = вР - a and a > sup f ^(x) + Mp 1 exp(1)^p 1 (x) + a\ Q V ^(x)J

в > sup f ^x) + Mq—1 exp(1)^q—1 (x) +

Q V nx)

It is easy to see that aq — в > 0 for pq > 1 and aq — в C 0 for pq C 1. Obviously, (e, e) is a subsolution of (3) in QT for any T. Let us show that f (x, t) = M exp(at) ^(x), g(x, t) = M exp(вt) ^(x)

is a supersolution of (3) in Q t for T C min if pq C 1 - Indeed, by (5) we have

- 1

у a , в , aq — в J

if pq >  1 , and for T C min

(a, i)

f t ( x, t ) — A f ( x, t ) — g ^p ( x, t ) + af r ( x, t ) — aE^r

= aM exp( at ) ^ ( x ) — A ^ ( x ) M exp( at ) — M ^p exp( вpt ) ^ ^p ( x ) + aM ^r exp( art ) ^ r ( x ) — aE^r

^ M exp( at ) ^ ( x ) (а ^Ц \      ^^{( x )}

-

M ^{p 1} exp(( вp — a ) t ) ^ ^{p 1} ( x ) — a^ >  0

for (x,t) G Qt. Using (4), we obtain fV^ = M exP(at) ^^ ^ Mm exp(amt)K J pm (y) dy > J ф(x,y,t)f m(y,t) dy

ΩΩ for (x,t) G St. In a similar way we show that gt(x, t) — Ag(x, t) — f q(x, t) + bgs(x, t) — bes ^ 0 for (x, t) G QT, dg(V t) > У ^(x,y,t)gn (y,t) dy for (x, t) G ST.

Ω

And we have u o _£ ( x ) <  f ( x, 0) , v o _£ ( x ) <  g ( x, 0) for x G Q , which implies that ( f ( x,t ) , g ( x,t )) is a supersolution of (3) in Q T .

To prove the existence of a solution of (3) in Q T for some T let us define a set

B = {(h i ( x,t ) ,h 2 ( x,t )) G C ( Q t ) x C ( Q t ) :

e <  h i ( x,t ) <  f ( x,t ) , e <  h 2 ( x,t ) <  g ( x,t ) , h i ( x, 0) = u o _£ ( x ) , h 2 ( x, 0) = v o _£ ( x )} .

Obviously, B is a nonempty convex subset of C ( Q t ) x C ( Q t ) . Now we consider the following problem

u t = A u + v p — aur + aer, v t = A v + u q — bv s + be s ,	( x,t) G Q t , ( x,t ) G Q t ,
d u = J ф(x, y,t ) s m y,^ dy, Ω	( x,t ) G S t ,
dv = f ^ (x, y ,t) s n ( y,t ) dy, Ω	( x,t ) G S t ,
u ( x, 0) = u 0 £ ( x ) ,   v ( x, 0) = v 0 £ ( x ) ,	x G Q ,

where ( s i ,S 2 ) G B . Problem (6) has a classical solution, which is bounded in Q t for some T (see, for example, [26]). Let A be a map such that A ( s i ,s 2 ) = ( u,v ) . Denote the set of functions u as U and the set of functions v as V. In order to show that A has a fixed point in B we verify that A is a continuous mapping from B into itself such that AB is relatively compact. Since ( e, e ) is a subsolution of (6) in Q t and ( f ( x, t ) ,g ( x, t )) is a supersolution of (6) in Q T we have that A maps B into itself thanks to a comparison principle for (6) which can be proved in a similar way as Theorem 3 below.

Let G ( x, t ; £, т ) denote the Green function for the heat equation given by u _t — A u = 0 for x G Q , t >  0 with homogeneous Neumann boundary condition. The Green function has the following properties (see [27, 28]):

G ( x,t ; £,r ) ^ 0 , x,^ G Q , 0 <  т                         (7)

sup

Ω

У G ( x, t ; £,r ) d^ = 1 , x G Q , 0 <  т < t,

Ω

t

У У G ( x, t ; £, т ) dS ^ dT <  X ^t— s, s ∂ Ω

0 < t — s <  a,

for s ^ 0 , X> 0 and small a >  0 .

It is well known that ( u ( x,t ) ,v ( x,t )) is a solution of (6) in Q t if and only if

t

u ( x,t ) = J G ( x,t ; y, O) u o _£ ( y ) dy + G J G ( x,t ; у,т ) ( v ^p ( y,T )

Ω

0Ω

— au r ( у, т ) + ae^r ) dy dT

t

+ G ! ^G(x,t ; ^GT ) (/ ^ф(^у^{,т )s} m ⁽ y ^,T ) dy \ ds ^dT , 0 ∂ Ω              Ω

t

v ( x, t ) = J G ( x

Ω

,t ; y, O) v o _e ( y ) dy + У G ^^y y,T )( u q ( y,T ) — bv ^s ( y,T )+ be s ) dydT

+G / G(x,t; GT) (/ ^(^y,T)sn (y,T) dyj ds dT 0 ∂Ω              Ω for (x, t) £ QT.

We claim that A is a continuous map. In fact let { ( s i k , S 2 k ) } be a sequence in B converging to ( s i ,s 2 ) £ B in C ( Q t ) x C ( Q t ) . Denote ( u k ,v k ) = A ( s i k ,S 2 k ) . Then by (7), (10), (11) we have

| u — U k | + | v

—

t vk^//

0Ω

G ( x,t ; y,T ) | v ^p

— v^p _k | dy dT +

t

J J G ^(x, t ; y ^,T")\ u q

— u k | dydT

t

+ a / G ( x,^X'y, y,T ) \ u r

t

— u k | dydT + b J J G ( x,t ; y,T ) | v ^s

— v s | dydT

+sup | s m

Q _T

—

t smk | / / G(x,t GT)(G ф(^,y,т) dy] dsdT

0 ∂ Ω t

Ω

+ sup | s n

Q _T

—

s n | G G ^G(x,t ; ^Gt ) ⁽ G ^y^ ) dy ^] ds ^dT

0 ∂Ω

< Ф(sup | u

Q T

t

—

Ω uk | + sup |v — Vk |)

Q T

+sup | s m

Q _T

—

s m | / / ^G(x,t ; ^GT ) ⁽ G ^ф( ^ ^, y ^,т ) dy ^] ds ^dT

0 ∂ Ω t

Ω

+ sup | s n

Q _T

—

s n | GG^G(x, t ^^,t ) ⁽ G^y^ ) dy ^] dsdT

0 ∂Ω

Ω

where

Ф =

maxi e^p 1, sup g^{p 1} ( x,t )l+ q max I e q ¹ , sup f ^{q 1} ( x,t)l Q T                            Q T

+ ar max e r ^{- 1} , sup f ^{r - 1} ( x,t ) + bs max e s ^{- 1} , sup g ^{s —} ( x,t ) > sup / / G ( x,t ; y,T ) dydT.

Q T                             Q T              Q T

0Ω

By (8) and (9) there exists T, such that Ф <  1 . Then we obtain ( u k , V k ) ^ ( u, v ) in C ( Q t ) x C ( Q T ) as k ^ ™ .

By the definition of B the sets U and V are uniformly bounded.

Now we prove the equicontinuity of the sets U and V. We will consider the set U since the proof for the set V is similar. We show that for any e> 0 there exists 6 >  0 , such that

| u ( x 2 ,t 2 ) - u ( x i ,t 1 ) | <  e

for any u ( x,t ) E U and any ( x 1 ,t 1 ) , ( x ₂ ,t 2 ) E Q T with the property | ( x ₂ ,t ₂ ) — ( x 1 ,t 1 ) | < 6. Applying (10), we obtain

| u ( x 2 , t 2 )

—

u ( x i ,t i ) | <  У

( G ( x 2 , t 2 ; y, 0) — G ( x i ,t i ; y, O) u o _£ ( y )) dy

Ω

t 2

+

У У G(x2,t2; y,T)(vp(у,т) — aur(у,т) + aer) dydT 0Ω t1

J У G ( x i ,t i ; у,т )( v p ( у,т ) — au^r ( у,т ) + ae^r ) dydT 0Ω

+

G ( x 2

∂ Ω

,t 2 ;

^{ф (} ^,у^{,т )s} m ^yT ) dy

dS ξ dτ

t i                        /

- !/Gx i ’t i ; ^ ^,T ) I У ^ф(^у^{,т )s} m ⁽ y ^,T ) dy 0 ∂ Ω                 Ω

dS ξ dτ

Since J_Q G ( x,t ; y, 0) u o _£ ( y ) dy is a continuous function in Q t (see [29])

У ( G ( x 2 ,t 2 ; y, 0) — G ( x i ,t i ; y, O)) u o _£ ( y ) dy

Ω

< 3

for small values of δ.

Let us consider the second term in the right hand side of (13). We set h ( y, t ) = v p ( y, t ) — au r ( y,T ) + ae r , H = sup Q T | h ( y,T ) | and suppose for the definiteness that t 2 ^ t i . Using (7), (8) and the continuity of the Green’s function for t >  t ^ 0 , we have

t 2

/ / G(X 2

Ω

,t 2 ; y,T ) h ( y,T ) dydT

t 1

J J G ( x i ,t i ; y,T ) h ( y,T ) dydT

0Ω

< H

t 2

/ / ^G(x 2

,t 2 ; y,T ) dydT +

t 1 - γ Ω

t 1 - γ

У У | G ( x 2 ,t 2 ; y,T ) — G ( x i ,t i ; y,T ) | dydT

t 1

+

У У G ( x i ,t i ; y,T ) dydT >

ǫ

< 3

t1 -γ Ω with an appropriate choice of γ and δ.

Similarly, we estimate the third term in the right hand side of (13)

t 2

f I G ( X 2 ,t 2 ; ^,T )

0 ∂ Ω

dSξ dτ t1

11 G ( xi,ti ; £,t )

0 ∂ Ω

dS^ dr <^

for small values of δ. From (13)–(16) we derive (12).

The Ascoli–Arzel´a theorem guarantees the relative compactness of AB. Thus we are able to apply a corollary of the Schauder–Tikhonov fixed point theorem (see [30]) and conclude that A has a fixed point in B if T is small. Now if ( u _£ ,v _£~ ) is a fixed point of A then it is a solution of (3) in Q T . The uniqueness of the solution follows from a comparison principle for (3) which can be proved in a similar way as Theorem 3 in the next section. >

Now we are ready to prove the existence of a local solution of (1).

Theorem 2. For small values of T problem (1) has a maximal solution in Q T .

<1 Now, let £ 2 > £ 1 . Then it is easy to show that ( u _£ 2 ( x,t ) ,v _£ 2 ( x, t )) is a supersolution of problem (3) with e = E i in Q t for some T. Applying a comparison principle to problem (3), we have u _£ 2 ( x,t ) ^ u _£ 1 ( x,t ) and v _£ 2 ( x,t ) ^ v _£ 1 ( x,t ) in Q t . Using the last inequalities and the continuation principle of solutions we deduce that the existence time of ( u _£ ( x,t ) ,v _£ ( x,t)) does not decrease as e g 0 . Taking e ^ 0 , we get

U max ( x, t ) = lim U £ ( x, t ) >  0 ,   V max ( x, t ) = lim v^x, t ) >  0 ,

ε → 0                            ε → 0

and ( u _max ( x,t ) ,v _max ( x,t )) exists in Q t for some T . By dominated convergence theorem ( u _max ( x, t ) , v _max ( x, t )) satisfies the following equations:

t

U max ( x, t ) = J G ( x, t ; y, Ω

⁰⁾ u o ⁽ y) dy + У У G ^(x,t ; у ^,т )« ах ⁽ y ^,T )

- au max ⁽ y ^,T )) dyd ^T

0Ω

t

+/1G(x,t; GT) (У ф(^у,т )umax (y,T) dy dSξ dτ,

0 ∂Ω               Ω

V max ( x,t ) = У G ( x,t ; y, Ω

t

0) v o ( y ) dy + У У G ( x,t ; y,T ) (u max

⁽ y ^,T ) - bv max ⁽y,T )) dyd ^T

t

+ / / G(x,t; ^,T) ( У Ф(^У,Т)vnax(y,T) dy 0 ∂Ω               Ω dSξ dτ.

By the properties of the Green function ( u _max ( x,t ) ,v _max ( x,t)) is a solution of (1) in Q t . Let ( u (x,t') ,v (x,t')') be another solution of (1) in Q t . Applying a comparison principle to problem (3), we have u _£ ( x,t ) ^ u ( x,t ) , v _£ ( x,t ) ^ v ( x,t ) in Q t . Taking e ^ 0 we deduce that u _max ^ u ( x,t ) , v _max ^ v ( x,t ) in Q T . Therefore, ( u _max ( x, t ) , v _max ( x,t )) is a maximal solution of (1) in Q T . >

• 3.    Comparison Principle

We start this section with a comparison principle for problem (1).

Theorem 3. Let ( u ( x, t ) ,v ( x, t )) and ( u ( x, t ) ,v ( x, t )) be a supersolution and a subsolution of problem (1) in Q t , respectively. Suppose that u ( x,t ) >  0 or u ( x,t ) >  0 in Q t U Г т and v ( x,t ) >  0 or v ( x,t ) >  0 in Q T U Г _т if min( p,q,m,n ) <  1 . Then u ( x,t ) ^ u ( x,t ) and v ( x, t ) ^ v ( x, t ) in Q T U Г _т .

• <1 Suppose at first that

min( p, q, m, n ) >  1 .                                   (18)

Let functions u o _£ ( x ) , V o _£ ( x ) have the same

0 C u o _£ ( x ) — u ( x, 0) <  2 £,

Then problem (1) with u o ( x ) = u ( x, 0) , ( u max ( x,t),V max ( x,t)), and, moreover,

U max ( x,t ) = lim u _£ ( x,t ) ,

ε → 0

properties as in the previous section but

0 C v o _£ ( x ) - v ( x, 0) C 2e.                 (19)

Vo(x) = v(x, 0) has a maximal solution vmax(x, t) = lim v£(x, t),

ε → 0

where ( u _£ ( x,t ) v _£ ( x,t )) is a solution of (3). To establish the theorem it is enough to prove that

U(x, t) C Umax(x, t) C u(x, t),   V(x, t) C Vmax(x, t) C v(x, t) in Qt0 U St0(20)

for any To G (0,T). We show only that umax(x,t) C u(x,t), Vmax(x,t) C v(x,t) in Qto U Sto(21)

for any To G (0, T) since the proof of other inequalities in (20) is similar. We set w1(x,t) = u£(x,t) — u(x,t), w2(x,t) = v£ (x,t) — v(x,t).(22)

W t C A w 2 + q0 3 - 1 w i — bs0 S - 1 W 2 + b£ ^s ,      ( x,t ) G

^Vx- C f ^y^mffm-'Ui^t) dy,     (x,t) G

Ω

^‘q^ ^C f ^ ^(x , y, t j nO n-^ t y, t ) dy,        ^(x , t ) ^G S T 0 ,

Ω

^w1(x, 0) C 2e, w2(x, 0) C 2£,                 x G Q, where 0i, i = 1,4, 6, are some continuous functions in Qt between v£(x,t) and v(x,t), and 0i, i = 2, 3, 5, are some continuous functions in Qt between u£(x, t) and u(x, t). Based on the assumptions made, we have

0 C u(x,t) C M, 0 C v(x,t) C M, £ C u£(x,t) C M, £ C v£(x,t) C M in QT0 , (24)

0 C Ф(х,У,^ C M and 0 C ^(x,y,t) C M in dQ x QT0, where M is some positive constant. It follows from (24) that powers of 0i, = 1,..., 6 in (23) are positive bounded functions in QT0, and, moreover, 0^ 1 C Mp-1, Sq -1 C Mq-1, ^m-1 C Mm-1, 0^-1 C Mn-1. Let us define the functions w1(x, t) = f (x, t) + £1 exp(at)h(x), w2(x, t) = g(x, t) + £1 exp(at)h(x),

where

h ( x ) G C 2 (Q) , h ( x ) >  1 in Q , ^xff > {_тм m + nM n j у h ( y dy on d Q ,

Ω

£ 1 = 2 e + e r + e s , a> max ^(x) + pM ^{p 1} + qM ^{q 1} + a + b.         (27)

q    h ( x )

We substitute the functions from (25) into the first inequality of (23) to derive ft(x,t) + ae1 exp(af)h(x) < Af (x,t) + £1 exp(at)Ah(x) + p ^p 1(x,t)g(x,t)

+ p^ p 1 ( x,t ) e 1 exp( at ) h ( x) — ar0 2 -¹ ( x,t' ) f ( x,t ) — ar0 2 ^-1 ( x,t ) e 1 exp( at ) h ( x ) + ae^r in Q T 0 .

Hence by (26), (27) we get ft(x,t) < Af(x,t) + pep-1(x,t)g(x,t) — ar0r-1(x,t)f(x,t) in Qt0.        (28)

In a similar way we obtain gt(x, t) < Ag(x, t) + q03—1(x, t)f (x, t) — bs 0s-1(x, t)g(x, t) in Qt0 .

Substituting the functions from (25) into the third and fourth inequalities of (23), we deduce

that	d^ ) <  J ф(x, y ,t)m ^ m 1( y ,t)f Ш) dy on ST o               (29) Ω
and	dv    <  У ^ (x, y ,t)n ^ 6 1 ( y ,t) g ( y ,t) dy on S T o . Ω

From (23), (25), (27) we have f (x, 0) < 0, g(x, 0) < 0 in Q. We prove that f (x,t) < 0,  g(x,t) < 0 in Qto U Sto .                       (30)

Let (30) not be true. Then there exists ( x o ,to) G Q t ₀ U S t ₀ such that t o >  0 , f ( x,t ) <  0 , g ( x,t ) <  0 for 0 <  t < t o and f ( x o ,t o ) = 0 or g ( x o ,t o ) = 0 for some x o G Q . Suppose that f ( x o ,t o ) = 0 . If x o G Q , then f t ( x o ,t o ) = 0 , A f ( x o ,t o ) <  0 and by (28) we get

0 = f t ( x o ,t o ) <  A f ( x o ,to) + p0 p ^{- 1} ( x o ,t o ) g ( x o ,t ₀ ) <  0 .

If x o G d Q , then (29) yields

0 ^ ^df ( x o ,^{t o )} < J ф ( x o ,y,t o ) m0 m ^{- 1} ( y,t o ) f ( y,t o ) dy <  0 . Ω

If g ( x o , t o ) = 0 we can obtain a contradiction in a similar way.

Taking e ^ 0 in (30) and using (22), (25)-(27), we deduce (21).

If (18) doesn’t hold we can introduce W 1 = u ( x, t ) — u ( x, t ) , U 2 ( x, t ) = v ( x, t ) — v ( x, t ) and prove the theorem in a similar way using the positiveness of some functions in a subsolution and a supersolution. >

Remark. Under the condition min( r, s ) <  1 we don’t suppose the positiveness of a subsolution or a supersolution in Theorem 3. A comparison principle for problem (1) with zero Dirichlet boundary condition is proved in [23] for the case min( r, s ) <  1 under the conditions u ( x, t ) >  0 and v ( x, t ) >  0 in Q _T .

To prove the uniqueness of a solution of problem (1) we need the following statement.

Lemma. Let ( u, v ) be a solution of (1) in Q t . If min( r, s ) ^ 1 and u o ( x ) = 0 or v o ( x ) = 0 in Q , then u ( x, t ) >  0 and v ( x, t ) >  0 in Q t U S t . If u o ( x ) >  0 and v o ( x ) >  0 in Q and either p < r <  1 , q < s <  1 or max( r, s ) ^ 1 , then u ( x, t ) >  0 and v ( x, t ) >  0 in Q T U Г _т .

<1 Let min( r, s ) ^ 1 and u o ( x ) = 0 in Q . Denote

M = sup u ( x, t ) ,

Q T 0

where T o G (0 ,T ) . We set h ( x,t ) = u ( x, t ) exp( At ) with A >  aM ^r 1 . Then we have in Q t ₀

h _t — A h = exp( At )( Au + u _t — A u ) >  exp( At ) u (A — au r 1) >  0 .

Since h ( x, 0) = u o ( x ) ^ 0 and u o ( x ) = 0 in Q , by the strong maximum principle h ( x,t ) >  0 in Q t ₀ . Let h ( x o ,t o ) =0 at some point ( x o ,t o ) G S t ₀ . Then according to Theorem 3.6 of [31] it yields dh ( x o ,t o ) /dv <  0 , which contradicts the boundary condition for u in (1). Hence u ( x, t ) >  0 in Q t U S t since T o may be any in (0 , T ) .

We show that

v ( x,t ) >  0 in Q T U S T .                             (31)

If either v o ( x ) = 0 or v o ( x ) = 0 and there is no т G (0 , T o ) , such that

v ( x, t ) = 0 in Q _T ,

then we prove (31) as above. If there exists т G (0 ,T o ) , such that (32) holds, then we have a contradiction in Q _τ with the second equation in (1).

Suppose now that u o ( x ) >  0 and v o ( x ) >  0 in Q and p < r <  1 , q < s <  1 . Let

£ 2 = min { min u o ( x ) , min v o ( x ) , ( | ^     , ( b ^    { .

It is easy to see that ( £ 2 , £ 2 ) is a subsolution of (1) in Q t and by Theorem 3 u ( x,t ) ^ £ 2 and v ( x, t ) >  £ 2 in Q T U Г _т .

If u o ( x ) >  0 and v o ( x ) >  0 in Q and s ^ 1 , then arguing as above, we obtain

v(x,t) > £3 in QT U Гт for some £3 > 0. Set

ε ^p r ¹

£ 4 = min < min u o ( x ), —     >.

Ω a

Then u(x, t) = £4 is a subsolution of the following problem ut = Au + vp — aur,               (x, t) G QT,

< ^du dxr ⁾ = / ^ф(x, y ^,t' ) ^{u m (} y ^{,t )} dy,      ^(x,t^{) G} S T ,

Ω

^u ( x, 0) = u o ( x ) ,                       x G Q .

Now by the comparison principle for (33) we conclude that u ( x, t ) ^ £ 4 in Q t U Г т . The proof is similar in the remaining case. >

As a simple consequence of Theorem 3 and Lemma, we get the following uniqueness result for problem (1).

Theorem 4. Let ( u,v) be a solution of (1) in Q t . Suppose that at least one of the following conditions holds:

• 1)    u ( x, t ) >  0 and v ( x, t ) >  0 in Q T U Г _т ;

• 2)    min( p, q, m, n ) ^ 1;

• 3)    min( p, q, m, n ) <  1 , u o ( x ) >  0 and v o ( x ) >  0 in Q and either p < r <  1 , q < s <  1 or max( r, s ) ^ 1 .

Then a solution of problem (1) is unique in Q T .

Now we show that problem (1) may have a nonunique solution in Q T .

Theorem 5. Let u o ( x ) = v o ( x ) = 0 and at least one of the following conditions hold:

• 1)    pq <  1 , r > Xp and s >  ^ for X G [q, 1] ;

• 2)    min(1 ,r ) >  m and ф ( x,y 1 ,t 1 ) >  0 for any x G d Q and some y i G d Q and t i G [0 , T );

• 3)    min(1 , s ) > n and ^ ( x, y 2 , t 2 ) >  0 for any x G d Q and some y 2 G d Q and t 2 G [0 , T ) . Then problem (1) has a nonunique solution in Q T .

• < 1 We note that problem (1) with trivial initial datum u o ( x ) = v o ( x ) = 0 has the trivial solution (0 , 0) . As we showed in Theorem 2 a maximal solution ( u _max ( x,t ) ,v _max ( x,t )) satisfies (17), where ( u _s ( x,t ) ,v _s ( x,t )) is some positive in Q t supersolution of (1). To prove the theorem we construct a nontrivial nonnegative subsolution ( u ( x, t )) , v ( x, t ) of (1) with trivial initial datum. By Theorem 3 then we have u _£ ( x,t ) ^ u ( x,t ) , v _£ ( x,t ) ^ v ( x,t ) and therefore a maximal solution is nontrivial.

Let the conditions 1) hold. We put

u ( x,t ) = ( Ctw ( x,t )) ^a , v ( x,t ) = ( Ctw ( x,t )) ^e ,                    (34)

where positive constants C, а, в will be chosen later and w(x,t) is a solution of the following problem wt = Aw,          (x,t) G Qt,

< w ( x,t ) = 0 ,            ( x,t ) G S T ,

^w ( x, 0) = w o ( x ) ,     x G Q .

Here w 0 ( x ) is a bounded nontrivial nonnegative continuous function, which satisfies the boundary condition. By the strong maximum principle

0 < w(x,t) < M = sup wo(x) for (x,t) G QT.(35)

x ∈ Ω

We note that

u(x, 0) = v(x, 0) = 0 for x G Q and ~d ’   ^ 0,   ~d ’ C 0 for (x, t) G ST.(36)

Suppose at first that в = aq +1, where a ^ i+pq ■ Then a ^ вР + 1.

We put X = aq+1. It is easy to check that X takes all values in (q, p—1 ] if a takes all values in [ 1+pq, °°). Since r > Xp and s > q for X G (q, p+1 ] we have ar — ep > 0, es - aq > 0.

By virtue of (34)–(39), after simple calculations we obtain ut — Au — vp + aur < ata-1(Cw(x, t))a — (Ctw(x, t))ep + a(Ctw(x, t))ar

• <    ( Ctw ( x, t )) ^e p {aT ^{a - ep - 1} ( CM ) ^{а - вр} + a ( CTM ) ^{ar - e} p — 1 } ^ 0 ,          (40)

v _t — A v — u q + bv s <  et ^{e -1} ( Cw ( x, t )) ^e — ( Ctw ( x, t )) ^aq + b ( Ctw ( x, t )) ^e s

• <    ( Ctw ( x, t )) ^aq {вСМ + b ( CTM ) ^e s ^{- aq} — 1 } <  0                (41)

for ( x,t) G Q t if C is sufficiently small. It is easy to see that (40), (41) hold for r > qp and s >  1 under suitable choice of a and C. Thus by (36), (40), (41) we conclude that ( u ( x, t ) , v ( x, t )) is a nontrivial subsolution of (1) with trivial initial datum and the theorem is proved for A G [q, p +j] . To prove the theorem for A G (p +l , p] we put a = вР +1 with в ^ 1 —pq and argue in a similar way.

Now we suppose that the conditions 2) hold. Let us consider the following problem ut = Au — aur,                     (x, t) G QT,

• <    ^du_d x— = f ^^x, y ^,t)u m ⁽ y,t) dy,     ⁽ x,t ) ^G S T ,                  (42)

^u ( x, 0) = 0 ,                             x G Q .

It is proved in [9] that (42) has a nontrivial nonnegative solution u n ( x,t ) . Then a pair of functions ( u n ( x,t), 0) is a nontrivial subsolution of (1) with trivial initial datum.

The remaining case can be treated similarly. >