Интеграция дискретности и непрерывности при формировании математической картины мира обучающихся

This is an Open Access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted reuse, distribution, and reproduction in any medium provided the original work is properly cited.

Одним из главных принципов отбора содержания обучения математике на каждой ступени образования является принцип целостности содержания, интеграции отдельных его компонентов в единое целое. В настоящее время при изучении математики этот принцип не всегда соблюдается, конкретный материал не формируется в систему знаний; обучающийся чаще всего не в состоянии самостоятельно ее структурировать и осмыслить. В статье в качестве интегрированной системы представлений об общих закономерностях и свойствах объективного мира, специфической формы интеграции и систематизации знаний рассматривается научная кар- тина мира, в которой проявляется качественное обобщение и соединение различных научных мировоззрений и теорий. Математические знания складываются в специальную математическую частнонаучную картину мира. Поэтому формирование математической картины мира является одной из главных задач обучения математике.

Для получения целостного понимания математики требуется стремиться к единству разных взглядов на предмет математики и ее природу. Однако имеется ли у ученых-математиков единое представление о предмете и природе своей науки? Как выразился М. Клайн, «каждое крыло здания математики претендует на роль единственно истинного храма»1. Позиции ученых значительно расходятся, нет единой точки зрения даже на предмет математики. Как ранее отмечено автором, «долгие годы считалось, что предметом математики являются числа и фигуры. Ф. Энгельс вместо этих терминов предложил использовать термины “количественные отношения” и “пространственные формы”, чтобы подчеркнуть, что предмет математики – не плод чистого разума, а часть реального мира. Советские математики опирались на это определение, но признавали, что с появлением новых разделов его необходимо расширить. Группа французских математиков под псевдонимом Н. Бурбаки считала, что математика – это наука о специальных математических структурах»2. Эти структуры подразделяются на порядковые, алгебраические и топологические3. В. И. Арнольд, в противовес мнению Н. Бурбаки, отмечал, что математика является частью теоретической физики и относится к числу естественных и экспериментальных наук4. Академик А. Н. Колмогоров в некоторых своих статьях поддержал точку зрения Н. Бурбаки. Ряд других математиков вместо термина математические структуры предпочитают использовать термин математические модели.

В математической картине мира важное место занимают представления о непрерывности и дискретности математических моделей, их взаимосвязях с реальным миром, представления о соотношении дискретности и непрерывности в математике, возможности их интеграции. Как показывает анализ литературы, среди ученых нет единства взглядов по этим вопросам, что нашло отражение во многих работах. Более того, имелись попытки свести матема- тику либо к непрерывности, либо к дискретности, что приводило к разрушению целостности математической картины мира, ее дезинтеграции.

Целью статьи является характеристика анализа трудностей на пути формирования целостной математической картины мира, вытекающих из наличия противоречия между дискретностью и непрерывностью в математике и математическом образовании, определение пути для разрешения данного противоречия, создание на этой основе рекомендаций, выполнение которых будет способствовать формированию у учащихся целостной математической картины.

Обзор литературы

Формированию научной картины мира у школьников посвящен целый ряд исследований. Одни исследователи пишут о математической составляющей естественно-научной картины мира, другие предпочитают использовать термин «математическая картина мира» [1–9]. Точка зрения автора по этому вопросу обоснована в монографии5. Философские взгляды на понятие научной картины мира, на соотношение между общенаучной и частнонаучными картинами мира различных областей научного знания, а также на этапы развития научной картины мира отражены в публикации автора [10] и работах Н. В. Бряник [11] и С. А. Лебедева [12].

По проблеме соотношения дискретного и непрерывного в математике и философии написаны десятки книг и сотни статей. В Древней Греции эта проблема была одной из основных как в философии, так и в математике, что нашло отражение в большинстве научных трактатов того времени. Как отмечается в нашей работе, «глубокие размышле-

ния античных философов приводили их к выводу о несовместимости принципов дискретности и непрерывности»6. Так, Демокрит следовал атомистическим, дискретным представлениям, полагая, что окружающий нас мир дискретен. Точки в пространстве он представлял как некие малые частицы (атомы), имеющие некоторый конечный объем.

На основе дискретных представлений Евдоксом и Архимедом для вычисления площадей различных криволинейных фигур был создан метод исчерпывания. Однако большинство древнегреческих ученых – современников Демокрита – отвергли дискретное истолкование геометрии. По мнению этих ученых (в частности Платона), такое понимание геометрии не отвечало самому духу математики, мешало разграничению математики и физики. Ренессанс дискретных идей начался лишь в XVII в. в трудах Кавальери, Кеплера и других ученых.

Непрерывные и дискретные модели конкурировали на первичном этапе разработки начал математического анализа. По мнению Лейбница, имеются неделимые или непротяженные элементы, поскольку иначе ни начало, ни конец движения невозможны. Он ввел бесконечно малые величины, которые называл инфинитезимальными и которые были больше нуля, но в то же время меньше другого любого положительного числа. Самым слабым местом созданной им теории была несогласованность с аксиомой Архимеда, имевшей интуитивную ясность.

В XIX в. «большинство математиков, исходя из потребностей строгого логического обоснования исчисления бесконечных малых, пошли по другому пути, фактически изгнали идеи дискретности из математического анализа, что отдалило математику от реальности»7. Создатели классического математического анализа придали основным понятиям математического анализа гораздо бóльшую строгость, чего им не хватало до этого. Однако, по мнению Дж. Уитроу, все эти ученые (Вейерштрасс, Коши, Дедекинд и др.) придерживались формальных взглядов на природу математики8. В период доминирования непрерывной математики некоторые ученые все же пытались выдвинуть идеи дискретности. В частности, во второй половине XIX в. профессор Московского университета Н. В. Бугаев, опираясь на некоторые параллели между теорией чисел и математическим анализом, стремился построить новую науку о «прерывных» функциях, которую назвал аритмологией. Он писал: «…математика распадается на два громадных раздела: теорию непрерывных и теорию прерывных функций... Разнообразие форм, под которыми является прерывность, ведет к тому, что научные вопросы аритмологии часто бывают сложнее и труднее соответствующих вопросов анализа»9. Ученый подчеркивал взаимосвязь и взаимодополняемость в математике аналитического и аритмо-логического подходов: «Мы видели, что в области чистой математики непрерывность и прерывность суть два понятия, несводимых одно к другому..., между ними должны устанавливаться не противоречия, а гармония»10.

П. А. Флоренский (ученик Н. В. Бугаева) также занимался вопросами соотношения между непрерывностью и дискретностью. Во введении к своей диссертации он утверждает, что «есть чисто фактические данные, помимо отвлеченных, указывающие на прерывность многих сторон действитель- ности»11. «Широкое распространение в математике непрерывных методов объясняется плодотворностью методов дифференцирования и интегрирования»12.

Трудность решения проблемы непрерывности и дискретности, их соотношения в описании мира убедительно показали широко известные апории Зенона. Со времен Зенона многие ученые пытались найти все новые разрешения этих апориев. Тем не менее устраивающее всех разрешение апориев Зенона до настоящего времени не найдено. Как отмечено автором, «среди математиков очень распространенной была точка зрения, что с созданием математического анализа, теории бесконечно малых и предельного перехода апории Зенона были разрешены»13. Однако и это «разрешение» стало очередным заблуждением. В данном случае «…математический анализ игнорирует неудобный момент, напрямую связанный с апориями: вместо вызывающего сопротивление разума утверждения “стрела никогда не долетит до цели” появился всех устраивающий тезис “переменная никогда не достигнет своего предела”»14.

Р. Курант и Г. Роббинс пишут в своей книге: «Еще со времен Зенона и его парадоксов все попытки дать точную, математическую формулировку интуитивному физическому или метафизическому понятию непрерывного движения были безуспешными... Остается неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать ее основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие»15. Объявляя апории Зенона пустыми софизмами и отмахиваясь от них на протяжении двух с половиной тысячелетий, наука только показывала свою беспомощность перед феноменом античного разума.

В начале XX в. в теоретической физике происходят настоящие революционные перемены. В этот период М. Планк высказал предположение о дискретности физического воздействия, а А. Эйнштейн ввел дискретные представления в световые явления. В последующие годы вопрос об интеграции дискретных и непрерывных моделей рассматривали ученые, занимавшиеся квантовой механикой. Дискретные представления возникли и при разработке теории информации. А. Н. Колмогоров отмечал, что в процессах переработки и передачи информации ведущими являются дискретные механизмы.

Важной вехой в становлении идей дискретности в математике стало создание во второй половине XX в. нестандартного анализа, в котором вместо опоры на сложное понятие предела используются более наглядные инфинитезимальные методы, являющиеся интуитивно более ясными. Об этих методах со времен О. Коши и К. Вейер-штрасса забыли в математике. Старый метод неделимых только после работ А. Робинсона (1960 г.) получил надежную основу и полноправный статус раздела современной математики в виде нестандартного анализа. До Робинсона понятие бесконечно малого числа осуждалось как нестрогое, а иногда отмечалось как бессмысленное. Робинсон впервые доказал, что это понятие имеет точный математический смысл16.

Более подробный исторический обзор литературы по проблеме дискретности и непрерывности можно найти в книге белорусского ученого О. И. Мель-никова17 и в работе автора [13].

Материалы и методы

Методологической основой исследования являются философские взгляды на научную картину мира, которая рассматривается как некая особая форма систематизации и интеграции знаний. Кроме того, в исследовании важную роль играет тринитарная методология. Использовались также теоретические методы: анализ педагогической и методической литературы, исторический, сравнительно-сопоставительный и логический виды анализа развития математической картины мира и содержания математического образования.

Как уже отмечалось, у обучающихся необходимо сформировать не просто сумму знаний об отдельных элементах математики, а некоторую целостную интегрированную систему представлений о мире математики. Отечественными учеными, как философами, так и педагогами, в качестве такой интегрированной системы представлений об общих закономерностях и свойствах объективного мира, специфической формы интеграции и систематизации знаний предложено рассматривать научную картину мира, в которой проявляется качественное обобщение и соединение различных научных мировоззрений и теорий. По мнению В. С. Степина и Л. Ф. Кузнецовой, «научная картина мира – особая форма теоретического знания, репрезентирующая предмет исследования науки соответственно определенному этапу ее исторического развития, посредством которой интегрируются и систематизируются конкретные знания, полученные в различных областях научного поиска»18.

Научная картина мира – это составная часть научного мировоззрения, определяющая деятельность не только педагога-исследователя, но и школьного учителя. Она закрепляет в мировоззрении систему знаний о строении мира, обретенных на том или ином историческом этапе развития науки. Поскольку имеют- ся разные уровни интеграции знаний, то в научной картине мира выделяют различные ее типы. Так, специальной научной картиной мира обозначается горизонт интеграции знаний в частной науке, закрепляющий целостное видение предмета этой науки, которое формируется на определенном историческом этапе ее развития. Таким образом, вполне правомочно говорить о математической картине мира.

Как отметили В. С. Степин и Л. Ф. Кузнецова, «на современной стадии эволюции науки, характеризующейся резким усилением междисциплинарного синтеза знаний и повышением удельного веса междисциплинарных исследований», происходит «уменьшение уровня автономности специальных научных картин мира» и возрастание роли «общенаучной картины мира как единого системного образа Универсума»19. Поэтому математическую картину мира необходимо рассматривать не изолированно, а как составную часть общенаучной картины мира.

Как показано выше, в истории математики имелись неоднократные попытки нарушения баланса между непрерывными моделями и дискретными, попытки свести математику к одной их этих двух компонент. При этом становилось очевидным разрушение единства математической картины мира, ее дезинтеграции. Таким образом, процессы, протекающие в естествознании, информатике, математике, служат источником осознания необходимости выработки нового, более сбалансированного взгляда на природу математики, выражающего ее целостность, интеграцию в математике дискретных и непрерывных моделей.

Как показано автором, «объяснение попыткам свести математику либо к дискретности, либо к непрерывности можно найти в том, что в основе взглядов большинства ученых лежит традиционная методология, бинарное мышление»20. В основе традиционной методологии лежит дихотомия – разделение объекта или явления на две противоборствующие части. Такое разделение являлось характерным для классической науки в целом. Все простейшие структуры в науке имели вид бинарных противопоставлений: бытие – сознание, вещество – поле, дифференциация – интеграция, необходимость – случайность, материализм – идеализм и др. По такому же способу произошло и разделение на гуманитарные и естественные, прикладные и фундаментальные науки. В истории науки можно проследить, как доминанты периодически менялись в каждой бинарной оппозиции, а позднее противоборствующие стороны стали претендовать на равноправие. Если противоречия сосуществуют, то в наличии должно быть что-то третье, делающее возможным их примирение. Для объяснения примирения, интеграции противоборствующих сторон является необходимым присутствие еще одного, третьего фактора. Поэтому в качестве основы исследования и была выбрана тринитарная методология, используемая все шире в постнеклассическом мировоззрении, хотя начала этого мышления можно проследить значительно раньше.

В основе многих религий лежит триединое начало. В гегелевской диалектике широко применялись триады, описываемые известным выражением «тезис – антитезис – синтез». П. Флоренский рассматривал трихотомию как основу системы, он писал о триединстве в человеке – ума, чувства и воли.

В последние десятилетия целый ряд ученых стали широко применять тринитарную методологию. Большой вклад в развитие тринитарной методологии внес петербургский ученый Р. Г. Баранцев. Он отмечал, что «целостность системных триад создается тремя равноправными компонентами, лежащими в одном уровне (рацио, эмоцио, инту- ицио), каждая из которых определяет степень coвмещения двух других»21.

Тринитарная методология успешно использовалась разными авторами при анализе различных явлений. В частности, данная методология применялась автором к разрешению ряда бинарных противоречий. Так, отсутствие всеми принятого определения предмета математики с позиций этой методологии может быть прояснено тем, что математика выражает собой синтез трех равноправных составляющих: логики, интуиции и эксперимента. В содержании образования автором в соответствии с тринитарной методологией были рассмотрены три другие равноправные компоненты: фундаментальность обучения, гуманистическая ориентация обучения и практическая (прикладная, профессиональная) направленность обучения. Содержание обучения в целостном виде может быть определено лишь при достижении некоторого баланса между элементами этой триады. Для решения проблемы бинарных противоречий между этими компонентами, как показано автором, оказывается необходимым третий элемент триады как мера их компромисса, как условие их существования [14–16].

Результаты исследования

Подводя итог проведенному историческому анализу литературы, сошлемся на слова А. Н. Колмогорова: «По существу все связи между математикой и ее реальными применениями полностью умещаются в области конечного... Мы предпочитаем непрерывную модель лишь потому, что она проще»22. В связи с этим математические модели строились главным образом непрерывными. Аналогичную мысль высказал известный американский математик Д. Зайл-бергер. По его мнению, непрерывные модели создавались как вынужденные аппроксимации дискретного мира. Дискретный анализ в своей основе проще

непрерывного, но технически сложнее. Именно поэтому непрерывные модели в период, когда компьютеры еще отсутствовали, были необходимыми упрощениями, дававшими возможность математикам добиваться успехов в науке.

В связи с возрастанием в науке дискретных воззрений в последнее время значительно выросла роль работ по построению дискретных моделей, замечается значительный рост исследований как по теоретическим разделам дискретной математики, так и по ее приложениям. Если до последнего времени в науке доминировала непрерывная математика, а на долю исследований по дискретной математике приходилось всего несколько процентов, то в последние десятилетия объем исследований по дискретной математике вырос в десятки раз.

Отмеченные перемены в математике не могли не сказаться и на содержании математического образования. Во многих вузах был введен курс дискретной математики. В школе появились факультативные и элективные курсы по теории графов, алгебре высказываний, комбинаторике и другим разделам дискретной математики. Однако обособленное изучение отдельных разделов на факультативных занятиях и в элективных курсах уже не отвечает требованиям системного подхода в обучении математике, не способствует интеграции разных разделов математики в единое целое. Хотя имеются отдельные попытки составить интегрированный курс математики, но все они ограничивались одним из указанных выше направлений. Е. А. Перминовым были проведены методические исследования, которые показали, что вполне возможно разработать и внедрить школьный курс дискретной математики, даже более доступный для учащихся, чем курс математического анализа23.

В настоящее время роль дискретной математики в обучении неизмеримо возросла. Дискретная математика является интегрирующим, связующим звеном курсов математики и информатики, математической основой самых разнообразных видов моделирования с использованием компьютера. Тем не менее дискретные вопросы, несмотря на изменение в настоящее время их роли в математической картине мира, в школьном курсе пока отражаются примерно в той же степени, что и полвека назад, что мешает обеспечить гармоничное сочетание дискретного и непрерывного в изучении математики и в понимании ее характера. Соотношение дискретного и непрерывного в обучении математике всегда было предметом обсуждения и споров. Поэтому в содержании математического образования также необходимо разрешать противоречие между дискретностью и непрерывностью. Особенно остро необходимость решения проблемы противоречия между дискретностью и непрерывностью в математике стала проявляться в последние десятилетия в связи с возрастанием роли и места дискретных разделов математики в условиях компьютеризации общества. Для разрешения этого противоречия, как вытекает из тринитарной методологии, необходим третий элемент. В качестве такого третьего элемента, как меру компромисса между дискретностью и непрерывностью, вполне допустимо рассматривать фрактальность. Как установили последние физические исследования, Вселенная слагается из бесконечного количества вставленных друг в друга фрактальных уровней, которые имеют подобные характеристики. На основе этого и других фактов философы высказывают мнение, что фрактальность является одним из всеобщих структурных свойств бытия.

Одним из способов определения фрак-тальности является определение ее через самоподобие составляющих элементов. Под это определение попадают не только впечатляющие конструкции, полученные при помощи компьютерных программ, но и всем хорошо известные детские пирамидки, матрешки, художественные тексты (например, в сказках типа «Колобок», «Теремок», «Репка» и др.). Фрактал – это замечательное понятие математики, оказавшееся средством построения моделей, соответствующих многим природным и социальным явлениям. Поэтому фракталы стали использоваться в экономике, социологии, биологии, геофизике, радиофизике, языкознании, культурологии и во многих других научных областях.

Первые фрактальные множества появились в конце XIX – начале XX в., но они вызывали в то время скорее неприязнь и непонимание многих ученых-математиков. Один из создателей теории множеств Г. Кантор первым построил фрактальное множество из непрерывного объекта – отрезка путем удаления из этого отрезка неограниченное число раз интервалов разной длины. В результате получается дискретный объект – канто-рова пыль (рис. 1).

Однако большинство из фрактальных множеств в то время оставались без наглядного изображения, поскольку подходящие инструменты для воплощения свойства самоподобия тогда еще не были созданы. И только в конце XX в. с появлением компьютера уда-лость построить эти множества. Одним из первых построения на компьютере фрактальных множеств проделал американский ученый швейцарского происхождения Б. Мандельброт. Им же эти множества были названы фрактальными и было дано название новому течению в математике – фрактальной геометрии, направлению, сформировавшемуся достаточно давно, но не оформившемуся в отдельную отрасль математики из-

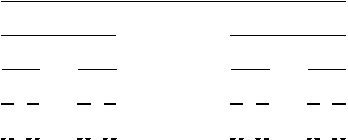
Р и с. 1. Множество Кантора (Канторова пыль) F i g. 1. Cantor set за отсутствия компьютерной техники еще в XIX в. Возрастающий интерес к фрактальной геометрии объясняется не только ее новизной, но и открывшимися перед современными науками о природе и обществе с появлением фракталов принципиально новыми возможностями. С открытием фракталов стала ясна ограниченность классического представления природы посредством гладких кривых и поверхностей. Окружающий нас мир значительно многообразнее, в нем оказалось достаточно много объектов, не попадающих в жесткие рамки евклидовой геометрии и допускающих фрактальное описание.

Как показывает ряд методических исследований, проведенных как в вузах, так и в средних учебных заведениях [17–22], изучение фрактальной геометрии вполне доступно как студентам, так и школьникам старших классов, вызывает у них большой познавательный интерес, способствует интеграции не только разных разделов математики, но математики и информатики, математики и искусства. Фракталы обладают заметной эстетической привлекательностью, чтобы почувствовать природную красоту фракталов, обрести эстетическое удовлетворение, практически не нужно каких-то дополнительных знаний. Это обстоятельство значительно упрощает изучение фрактальной геометрии школьниками и студентами.

Обсуждение и заключения

В исследовании проанализированы трудности, вытекающие из наличия долговременного противоречия между дискретностью и непрерывностью в математике и математическом образовании. Как показано выше, разрешить это противоречие можно с помощью фракталь-ности. Фрактальность вполне возможно трактовать как третий элемент, который необходим для разрешения антагонизма между дискретностью и непрерывностью в математике и математическом образовании, как меру их компромисса. Фрактальность наряду с дискретностью и непрерывностью является таким же

важнейшим структурным свойством материи. Фрактальная геометрия – это не просто новый раздел математики, это одна из важнейших составных частей математической картины мира, что определяет ее значение для обучения.

Таким образом, цель исследования достигнута: при помощи изучения фрак-тальности предоставляется создать возможность достижения интеграции дискретности и непрерывности в математике, решить важнейшую задачу обучения математике – сформировать у обучающихся целостную математическую картину мира. Изучение фрактальной геометрии в школе и в вузах способствует формированию у учащихся целостной математической картины мира, это средство интеграции дискретности и непрерывности при изучении математики, интеграции в обучении математики и информационных технологий.

СПИСОК

ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Поступила 14.01.2018; принята к печати 16.04.2018; опубликована онлайн 28.09.2018.

Об авторе :

Тестов Владимир Афанасьевич, профессор кафедры математики и методики преподавания математики ФГБОУ ВО «Вологодский государственный университет» (Россия, г. Вологда, ул. Ленина, д. 15), доктор педагогических наук, профессор, ORCID: ,

Автор прочитал и одобрил окончательный вариант рукописи .