Intelligent digitalization of cardiovascular risks

Автор: Gromov Y.Y., Gorbunov A.V., Tyutyunnik V.M.

Рубрика: Report

Статья в выпуске: 22, 2022 года.

Бесплатный доступ

The aim of the study was to develop a mathematical model of the risks of the cardiovascular system based on the selected factors affecting cardiovascular diseases (CVD) and to test the developed mathematical model on a sample of clinical examples. CVD risk factors was grouped by types: biological indicators (anthropometric, biochemical, morphological, physiological), disease indicators, social indicators. An assessment of the degree of risk for each of the indicators was carried out by calculating the degree of risk using the membership formula, then evaluating the hazard class (according to the degree of risk) using a logical-linguistic model and a training algorithm for the neural fuzzy classifier of the network. The correctness of the risk determination by the developed model was confirmed by the analyzed 60 verified cases of acute cerebrovascular accident (18 men and 42 women). The analysis of the test results of the constructed neuro-fuzzy classifier allows us to conclude that it works satisfactorily even when using incomplete information, which makes it possible to use it for prompt decision-making. The results of testing on clinical examples, with an acceptable level of significance of a type I error of 0.05, showed that the risk was determined correctly. The factors influencing the risk of CVD are identified and designated as the corresponding linguistic variables. A logical-linguistic model was built, from which a transition was made to a hybrid neuro-fuzzy classifier, which allows assessing the influence of the identified factors on the level of risk of CVD. As a result of approbation of the model of intellectual digitalization of risks of the cardiovascular system on real clinical examples, it was confirmed that the risk was determined correctly, which means that it is possible to assert about the prospects for introducing this model into clinical practice and guaranteeing medical specialist more accurate diagnosis and optimization of their activities.

Еще

Cardiovascular diseases, risk factors, mathematical model, hazard class, neuro-fuzzy classifier

Короткий адрес: https://sciup.org/148324644

IDR: 148324644 | DOI: 10.18137/cardiometry.2022.22.7794

Текст научной статьи Intelligent digitalization of cardiovascular risks

Yuri Y. Gromov, Aleksei V. Gorbunov, Viacheslav Mikhailovich Tyutyunnik. Intelligent digitalization of cardiovascular risks. Car-diometry; Issue 22; May 2022; p. 77-94; DOI: 10.18137/cardiom-etry.2022.22.7794; Available from: issues/no22-may-2022/intelligent-digitalization

Mortality from cardiovascular diseases (CVD) is far ahead of mortality from infectious and oncological diseases [1]. The World Health Organization (WHO) estimates that in 2012, for example, 17.5 million people died from CVD worldwide, representing 31% of all global deaths [2], and by 2030 about 23.6 million people will die from CVD each year [3]. CVD is the leading cause of death in the Russian Federation, accounting for 57% of the total mortality [4]. CVD is the most common cause of hospitalizations and disabilities of the population of the Russian Federation. The economic damage from the CVD in the Russian Federation is about 3% of the country’s gross domestic product [5]. These rates are still among the highest in the world, exceeding similar values in developed countries by 4–6 times [6].

In world practice, the risks of CVD are assessed on various scales, for example, on the Framingham scale or on a more complete scale Systematic Coronary Risk Evaluation (SCORE) [7–8]. But its assess only four factors, while the rest are simply ignored, despite the fact that it’s are included in various national recommendations [9–11]. There are similar scales for assessing the risks of diseases that indirectly affect the cardiovascular system. Such a scale exists to assess the risk of developing diabetes mellitus (DM) [12], it considers eight factors, while in reality there are much more [13]. It is worth noting that there is no scale that analyzes most of the CVD indicators listed in the clinical recommendations.

National recommendations from different countries highlight the following indicators affecting the risks of CVD: age, gender, body mass index, waist, low-density lipoproteins (LDL), triglycerides (TG), glycated hemoglobin (GH), glomerular filtration rate (GFR), diameter of the left ventricle (DLV), left atrial size (LAS), left ventricular ejection fraction (LVEF), systolic blood pressure (SBP), pulse (P). The presence of diseases is taken into account: DM, arterial hyper- tension (AH), myocardial infarction (MI), atrial fibrillation (AF), speech and motor disorders in the structure of neurological deficits, as well as social factors (smoking, alcohol consumption), hypodynamia, psy-chotraumatic and genetic factors [9–11, 13]. It should be noted that the current (2021) recommendations do not sufficiently say about the impact of coronavirus infection on CVD [14, 15]. At the same time, all these indicators affect the CVD, and there are also a large number of factors the influence of which on CVD is not fully understood [16].

Thus, there are an extensive number of factors affecting CVD, but there is no generally accepted unified assessment of these influences. Hence the obvious need to create a mathematical model of CVD risk factors in order to combine extensive but disparate information into one common actually working model.

To achieve this goal, the authors set the following tasks:

1) identify the most significant of CVD risk factors;
2) develop a mathematical model for assessing cardiovascular risk based on the identified factors;
3) to approbate the developed mathematical model.

Materials and methods

We propose to group the factors affecting the CVD by their types: biological indicators (anthropometric, biochemical, morphological, physiological), indicators of the presence of diseases, indicators of social factors. All indicators are ranked according to the degree of risk in accordance with the values of national recommendations [9–11, 13, 16].

Anthropometric indicators : age (A), gender (G), body mass index (BMI), waist (W). Indicators according to the degree of risk of a person’s: extremely high (over 70 years), very high (60-69 years), high (50-59 years), medium (40-49 years), low (30-39 years), and very low (up to 30 years). Indicators according to the degree of risk, depending on the sex of a person, are ranked as high in men and low in women. Indicators by the degree of risk depending on the BMI: high (more than 30.0 kg/m² ), medium (25.0–29.9 kg/m² ), low (8.5–24.9 kg/m² ). Indicators by the degree of risk of waist: high (more than 102 cm in men and from 94 to 102 cm in women) and low (from 88 to 102 cm in men and from 80 to 93 cm in women).

Biochemical indicators : amount of LDL, amount of TG, amount of GH (HbA_1c), GFR. Indicators on the degree of risk depending on the amount of LDL: 78 | Cardiometry | Issue 22. May 2022

high (3.0), medium (2.0), and low (1.4 mmol/l ). Indicators for the degree of risk depending on the amount of TG: high (more than 2.3), medium (1.7–2.2), low (less than 1.7 mmol/l ). Indicators of the degree of risk depending on HbA1c: high (3.5 and more), medium (5.5–6.4), low (less than 5.5 mmol/l ). Indicators of the degree of risk depending on GFR: high (less than 60 ml/min. ), medium (5.5–80 ml/min. ), low (more than 80 ml/min. ).

Morphological indicators : DLV and LAS. Indicators of the degree of risk from DLV: high (5.6 cm and more), low (up to 5.6 cm ). Indicators for the degree of risk depending on LAS: high (4.1–4.6 cm in men and 3.9–4.2 cm in women), low (3.0–4.0 cm in men and 2.7–3.8 cm in women).

Physiological indicators : LVEF, SBP, P. Indicators of the degree of risk of LVEF: high (less than 45 ml ), medium (45–54 ml ), low (55 ml and more). SBP risk indicators: high (above 140 mm Hg or below 90 mm Hg ), medium (120–139 mm Hg ), low (below 120 mm Hg but above 90 mm Hg ). Indicators of the degree of risk from P: high (more than 80 beats/min. and less than 50 bpm ), medium (60-80 bpm ), low (50-60 bpm ).

Nosological indicators : DM, AG, AF, MI, acute cerebrovascular accident (ACVA; speech, motor and other disorders in the structure of neurological deficits). Indicators for the degree of risk depending on the DM: very high (there are pronounced complications – polyneuropathy, nephropathy, diabetic foot), high (there are unexpressed complications, onset of polyneuropathy), medium (DM without complications), low (no DM). Indicators for the degree of risk of AG: very high (AG with the defeat of two or more target organs), high (AG with the defeat of one target organ), medium (AG without lesions of target organs), low (no AG). Indicators for the degree of risk of AF: high (there is a paroxysmal/persistent form), medium (there is a permanent form), low (no). Indicators of the degree of risk of MI: high (there is transmural MI), medium (there is non-transmural MI), low (no MI). Indicators by degree of risk depending on ACVA: very high (there is a neurological deficit for more than 21 days), high (there is a neurological deficit from 1 to 21 days), medium (there is a neurological deficit up to 1 day), low (there is no neurological deficit).

Social indicators: smoking (S), alcohol consumption (AC), hypodynamia (GD), psychotraumatic factors (PF), genetic factors (GF). Indicators for the degree of risk from S: high (more than 10 cigarettes per day), medium (less than 10), low (no). Indicators of the risk of AC (by alcohol): high (more than 150 g/ day in men, more than 100 g/day in women), medium (75–150 g/day in men, 50–100 g/day in women), low (0–75 g/day in men, 0–50 g/day in women). GD risk indicators: high (less than 5,000 steps per day), medium (5,000–10,000 steps per day), low (more than 10,000 steps per day). PF indicators: high (a person is not stress-resistant), medium (stress-resistant), low (no reaction to stress). GF indicators: extremely high (2 parents and all siblings under 50 years of age have any or a combination of ACVA, MI, AF, AH, DM), very high (2 parents and all sibs over 50 years old, or 1 parent or 1 sibs under 50 years old have any or a combination of ACVA, MI, AF, AH, DM), high (2 parents or all sibs over 50 years old, or 1 parent or 1 sibs under 50 years of age have any or a combination of ACVA,

MI, AF, AH, DM), low (1 parent or 1 cibs over 50 years of age have any or a combination of ACVA, MI, AF, AH, DM), very low (do not have any of ACVA, MI, AF, AH, DM).

Values and their ranges (for each of the indicators and for each degree of impact on CVD risks) were taken from national recommendations [9–11, 13]. However, it should be noted that we have introduced our own indicators to simplify their assessment in some cases. In addition to the indicators taken from the recommendations, we added our own scale 0–10 to each indicator, where 0 is the minimum and 10 is the maximum value of the indicator.

Based on linguistic variables (Table 1), we determined the hazard class: “Very High Risk” (VHR), “High Risk” (HR), “Medium Risk” (MR), “Low Risk” (LR), No Risk (NR).

Table 1

Linguistic variables, term sets, value ranges and membership functions

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
I. Biological indicators
Anthropometric
1. Age (A), years	Extremely high	Over 70	f ( x ) = 0; x < 70 „ _s 11 Г x - 100 ) „ f ( x ) = —+ —* cos ------ , 70 < x < 100 2 2 ( 30 )
	Very high	60-69	f ( x ) = 0; x < 60 , 11 Г x - 69 f ( x ) = — + — * cos ----- , 60 < x < 69 2 2 ( 9 ) f ( x ) = 0; x > 70
	High	50-59	f ( x ) = 0; x < 50 , 11 Г x - 59 f ( x ) = — + — * cos ----- , 50 < x < 59 2 2 ( 9 ) f ( x ) = 0; x > 60
	Medium	40-49	f ( x ) = 0; x < 40 „ , 11 Г x - 44 ^ f ( x ) = —+ —* cos ----- , 40 < x < 44 2 2 I 4 ) _ , 11 Г x - 49) f ( x ) =---* cos ------ , 44 < x < 49 2 2 I 5 J f ( x ) = 0; x > 50
	Low	30-39	f ( x ) = 0; x < 30 . 11 Г x - 39 ^ . f ( x ) =---* cos ------ , 30 < x < 39 2 2 ( 9 ) f ( x ) = 0; x > 40
	Very low	Up to 30	f ( x ) = 0; x > 30 x 11 Гx - 30 ) „ f ( x ) =---* cos ------ , 0 < x < 30 22 ( 30 )

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
2. Gender (G)	High	Male (5-10)	f ( x ) = 0; x > 0 „ _s 11 ( x - 10 ) f ( x ) = —+ —* cos ----- , 5 < x < 10 2 2 I 5 J f ( x ) = 0; x < 5
2. Gender (G)	Low	Female (0-5)	f ( x ) = 0; x > 5 . 11 ( x - 5 ) f ( x ) =---* cos ----- , 0 < x < 5 2 2 I 5 J f ( x ) = 0; x < 10
3. Body mass index (BMI)	High	Above 30	f ( x ) = 0; x < 30 „ _s 11 ( x - 40 ) _ f ( x ) = —+ —* cos ----- , 30 < x < 40 22 ( 10 J
	Medium	25-30	f ( x ) = 0; x < 25 „ x 11 (x - 27.5) „ f ( x ) = —+ —* cos ------- , 25 < x < 27.5 2 2 ( 2.5 J r, x 11 (x - 30 ) f ( x ) =---* cos ------ , 27.5 < x < 30 2 2 ( 2.5 J f ( x ) = x > 30
	Low	18,5-25	f ( x ) = 0; x < 18.5 „ x 11 (x - 25 ) _ f ( x ) =---* cos ------ , 18.5 < x < 25 2 2 ( 7.5 J f ( x ) = 0; x > 25
4. Waist (W), cm	High	Men (over 102)	f ( x ) = 0; x < 102 f ( x ) = —+ —* cos[ x —1^ \|, 102 < x < 110 2 2 ( 8 J
	High	Women (94-102)	g ( x ) = 0; x < 94 / x 11 ( x - 102 ) g ( x ) = —+ —* cos ------ , 94 < x < 102 2 2 ( 8 J g ( x ) = 0; x > 102
	Low	Men (88-102)	f ( x ) = 0; x < 88 1 1 x - 102Л f ( x ) =---* cos 11 , 88 < x < 102 2 2 ( 14 J f ( x ) = 0; x > 102
	Low	Women (80-93)	g ( x ) = 0; x < 80 _{z x} 11 ( x - 88 ) g ( x ) =---* cos ------ , 80 < x < 88 2 2 ( 8 J g ( x ) = 0; x > 88
Biochemical
5. Low-density lipoproteins (LDL), mmol/l	High	3,0 (7-10)	f ( x ) = 0; x < 7 r, x 11 (x - 10 ) f ( x ) = —+ —* cos ----- , 7 < x < 10 2 2 ( 3 J
5. Low-density lipoproteins (LDL), mmol/l	Medium	2,0 (4-6)	f ( x ) = 0; x < 4 x 11 (x - 5 ) , f ( x ) = —+ —* cos ---- , 4 < x < 5 2 2 ( 1 J \ 11 f x - 6 ^ f ( x ) =---* cos ----- , 5 < x < 6 2 2 ( 1 J f ( x ) = 0; x > 6

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Low	1,4 (0-3)	f ( x ) = 0; x > 3 „ _s 11 Г x - 3 ) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 )
6. Triglycerides (TG)	High	More than 2,3	f ( x ) = 0; x < 2.3 „ _x 11 Г x - 5) , „ , f ( x ) = —+ —* cos ---- , 2.3 < x < 5 22 ( 3.7 )
	Medium	1,7-2,3	f ( x ) = 0; x < 1.7 x 11 Г x - 2.0 ) , f ( x ) = —+ —* cos ------ , 1.7 < x < 2.0 2 2 ( 0.3 ) „ x 11 Г x - 2.3 ) f ( x ) =---* cos ------- , 2.0 < x < 2.3 2 2 ( 0.3 ) f ( x ) = 0; x > 2.3
	Low	Less than 1,7	f ( x ) = 0; x > 1.7 r, x 11 Г x - 1.7) „ f ( x ) =---* cos ------- , 0 < x < 1.7 2 2 ( 1.7 )
7. Glycated hemoglobin (HbA1c), mmol/mol	High	6,5 and more	f ( x ) = 0; x < 6.5 _r, x 11 Гx - 10 ) f ( x ) = — + — * cos ----- , 6.5 < x < 10 2 2 ( 3.5 )
	Medium	5,5-6,4	f ( x ) = 0; x < 5.5 r, x 11 Гx - 6.0 ) f ( x ) = — + — * cos ------ , 5.5 < x < 6.0 2 2 ( 0.5 ) „ x 11 Гx - 6.4) f ( x ) =---* cos ------- , 6.0 < x < 6.4 2 2 ( 0.4 ) f ( x ) = 0; x > 6.4
	Low	5,5 and less	f ( x ) = 0; x > 5.5 _x 11 Г x - 5.5 ) f ( x ) =---* cos ------ , 0 < x < 5.5 2 2 ( 5.5 )
8. Glomerular filtration rate (GFR), ml/min	High	Less than 60	f ( x ) = 0; x > 60 x 11 Г x - 60 ) f ( x ) = — + — * cos ----- , 0 < x < 60 22 ( 60 )
	Medium	60-80	f ( x ) = 0; x < 60 x 11 Гx - 70) _ f ( x ) = —+ —* cos ----- , 60 < x < 70 22 ( 10 ) x 11 Гx - 80) „ f ( x ) =---* cos ------ , 70 < x < 80 22 ( 10 ) f ( x ) = 0; x > 80
	Low	More than 80	f ( x ) = 0; x < 80 r, x 11 Гx - 100 ) _ f ( x ) =---* cos ------- , 80 < x < 100 2 2 ( 20 )
Morphological
9. Diameter of the left ventricle (DLV), cm	Big	5,6 and more	f ( x ) = 0; x < 5.6 r, x 11 Гx - 10 ) , f ( x ) = —+ —* cos ----- , 5.6 < x < 10 2 2 ( 4.4 )

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Small	Up to 5.6	f ( x ) = 0; x > 5.6 x 11 f X - 5.6 A „ , , f ( x ) =---* cos ------ , 0 < x < 5.6 2 2 ( 5.6 J
10. Left atrial size (LAS), cm	High	Men (4,1-4,6)	f ( x ) = 0; x < 4.1 „ x 11 f x - 4.6 A f ( x ) = —+ —* cos ------ , 4.1 < x < 4.6 2 2 ( 0.5 J f ( x ) = 0; x > 4.6
	High	Women (3,9-4,2)	f ( x ) = 0; x < 3.9 x 11 f x - 4.2 A „ „ , _ „ f ( x ) = — + — * cos ------ , 3.9 < x < 4.2 2 2 ( 0.3 J f ( x ) = 0; x > 4.2
	Low	Men (3,0-4,0)	f ( x ) = 0; x < 3.0 „ _s 11 f x - 4 A f ( x ) =---* cos ----- , 3 < x < 4 2 2 ( 1 J f ( x ) = 0; x > 4.0
	Low	Women (2,7-3,8)	g ( x ) = 0; x < 2.7 g ( x ) = — - — * cos[ x —— \|, 2.7 < x < 3.8 2 2 ( 1.1 J g ( x ) = 0; x > 3.8
Physiological
11. Left ventricular ejection fraction (LVEF), ml	High	Less than 45	f ( x ) = 0; x > 45 x 11 f x - 45 A f ( x ) = —+ —* cos ----- , 0 < x < 45 22 ( 45 J
	Medium	45-54	f ( x ) = 0; x < 45 „ x 11 fx - 50A _ f ( x ) = — + — * cos ----- , 45 < x < 50 2 2 ( 5 J „ x 11 f x - 54) f ( x ) =---* cos ------ , 50 < x < 54 2 2 ( 4 J f ( x ) = 0; x > 54
	Low	55 and more	f ( x ) = 0; x < 55 _r, x 11 f x - 64 ) f ( x ) =---* cos ------ , 55 < x < 64 2 2 ( 9 J
12. Systolic blood pressure (SBP), mm Hg	High	More than 140, less than 90	f ( x ) = 0; x < 140 1 1 f x - 160 A f ( x ) = —+ —* cos ------ , 140 < x < 160 2 2 ( 20 J g ( x ) = 0; x > 90 z z 11 f x - 90 A g ( x ) = —+ —* cos ----- , 0 < x < 90 22 ( 90 J
12. Systolic blood pressure (SBP), mm Hg	Medium	120-139	f ( x ) = 0; x < 120 . 11 (x - 129^ f ( x ) = - + -* cos ------ , 120 < x < 129 2 2 ( 9 J . 11 f x - 139 A f ( x ) =---* cos ------ , 129 < x < 139 22 ( 10 J f ( x ) = 0; x > 139

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Low	Less than 120	f ( x ) = 0; x > 120 „ _s 11 Г x - 120) „ f ( x ) =---* cos ------- , 0 < x < 120 22 ( 120 J
13. Pulse (P), bpm	High	More than 80, less than 50	f ( x ) = 0; x < 80 r, x 11 Гx - 100 ) f ( x ) = — + — * cos ------ , 80 < x < 100 2 2 ( 20 J g ( x ) = 0; x > 50 , . 11 Г x - 50 ) g ( x ) = —+ —* cos ----- , 0 < x < 50 22 ( 50 J
	Medium	60-80	f ( x ) = 0; x < 60 x 11 Гx - 70) „ f ( x ) = — + — * cos ----- , 60 < x < 70 22 ( 10 J x 11 Г x - 80 ) „ f ( x ) =---* cos ------ , 70 < x < 80 22 ( 10 J f ( x ) = 0; x > 80
	Low	50-60	f ( x ) = 0; x < 50 x 11 Г x - 60 ^ f ( x ) =---* cos ------ , 50 < x < 60 22 ( 10 J f ( x ) = 0; x > 60
II. Presence of diseases
1. Diabetes mellitus (DM)	Very high	There are pronounced complications (polyneuropathy, nephropathy, diabetic foot) (9-10)	f ( x ) = 0; x < 9 r, x 11 Г x - 10 ) „ f ( x ) = —+ —* cos ----- , 9 < x < 10 2 2 ( 1 J
	High	There are unexpressed complications (the beginning of polyneuropathy) (6-8)	f ( x ) = 0; x < 6 _x 1 1 Г x - 8 ^ „ f ( x ) = —+ —* cos ---- , 6 < x < 8 2 2 ( 2 J f ( x ) = 0; x > 8
	Medium	There are no complications (3-5)	f ( x ) = 0; x < 3 , 11 Г x - 4 ) f ( x ) = —+ —* cos ---- , 3 < x < 4 2 2 ( 1 J „ x 11. Г x - 5 ) . f ( x ) =---* cos ---- , 4 < x < 5 2 2 ( 1 J f ( x ) = 0; x > 5
	Low	No (0-3)	f ( x ) = 0; x > 3 x 11 Гx - 3) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 J
2. Arterial hypertension (AG)	Very high	There is a defeat of two or more target organs (9-10)	f ( x ) = 0; x < 9 r, x 11 Г x - 10) „ f ( x ) = — + — * cos ----- , 9 < x < 10 2 2 ( 1 J
2. Arterial hypertension (AG)	High	There is with the defeat of one target organ (6-8)	f ( x ) = 0; x < 6 x 1 1 Гx - 8 ^ „ f ( x ) = —+ —* cos ---- , 6 < x < 8 2 2 ( 2 J f ( x ) = 0; x > 8

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Medium	There is no defeat of target organs (3-5)	f ( x ) = 0; x < 6 _x 11 Г x - 7 ) , , f ( x ) = —+ —* cos ---- , 6 < x < 7 2 2 ( 1 ) x 1 1 Г x — 8 ^ _ f ( x ) =---* cos ----- , 7 < x < 8 2 2 ( 1 ) f ( x ) = 0; x > 8
	Low	No (0-3)	f ( x ) = 0; x > 3 r, x 11 Г x - 3 ) f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 )
3. Atrial fibrillation (AF)	High	There is a paroxysmal/ persistent form (7-10)	f ( x ) = 0; x < 7 r, x 11 Г x - 10 ) f ( x ) = — + — * cos ----- , 7 < x < 10 2 2 ( 3 )
	Medium	There is a permanent form (4-6)	f ( x ) = 0; x < 4 . 11 Г x - 5 ) f ( x ) = —+ —* cos ---- , 4 < x < 5 2 2 I 1 ) x 11 Г x - 6 ) f ( x ) =---* cos ----- , 5 < x < 6 2 2 I 1 ) f ( x ) = 0; x > 6
	Low	No (0-3)	f ( x ) = 0; x > 3 x 11 Гx - 3 ) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 )
4. Myocardial infarction (MI)	High	There is a transmural (7-10)	f ( x ) = 0; x < 7 r, x 11 Г x - 10 ) f ( x ) = —+ —* cos ----- , 7 < x < 10 2 2 ( 3 )
	Medium	There is a nontransmural (4-6)	f ( x ) = 0; x < 4 „ x 11. Г x - 5 ) , , _ f ( x ) = —+ —* cos ---- , 4 < x < 5 2 2 ( 1 ) X ^{1 1} . Г x ^- ⁶ 1 , f ( x ) =---* cos ----- , 5 < x < 6 2 2 ( 1 ) f ( x ) = 0; x > 6
	Low	No (0-3)	f ( x ) = 0; x > 3 x 11 Гx - 3 ) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 )
5. Acute cerebrovascular accident (ACVA): speech, motor and other disorders in the structure of neurological deficits	Very high	There is a neurological deficit for more than 21 days (9-10)	f ( x ) = 0; x < 9 r, x 11 Г x - 10) „ f ( x ) = — + — * cos ----- , 9 < x < 10 2 2 ( 1 )
	High	There is a neurological deficit from 1 to 21 days (6-8)	f ( x ) = 0; x < 6 ,, x 11 Гx- 8) , , f ( x ) = —+ —* cos ---- , 6 < x < 8 2 2 ( 2 ) f ( x ) = 0; x > 8
	Medium	There is a neurological deficit up to 1 day (3-5)	f ( x ) = 0; x < 3 , 11 Г x - 4 ^ f ( x ) = —+ —* cos ---- , 3 < x < 4 2 2 ( 1 ) x 11 Гx - 5 ) f ( x ) =---* cos ---- , 4 < x < 5 2 2 ( 1 ) f ( x ) = 0; x > 5

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Low	No (0-3)	f ( x ) = 0; x > 3 „ _s 11 f x - 3 ) f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 J
III. Social factors
1. Smoking (S) Smoking index (SI): experience, number of cigarettes = 20	High	SI more than 10 (7-10)	f ( x ) = 0; x < 7 „ _s 11 f x - 10 ) f ( x ) = —+ —* cos ----- , 7 < x < 10 2 2 ( 3 J
	Medium	SI less than 10 (4-6)	f ( x ) = 0; x < 4 . 11 f x — 5 ) f ( x ) = — + — * cos ---- , 4 < x < 5 2 2 I 1 J \ 1 1 f x — 6 ^ f ( x ) =---* cos ----- , 5 < x < 6 2 2 I 1 J f ( x ) = 0; x > 6
	Low	No (0-3)	f ( x ) = 0; x > 3 „ _s 11 f x — 3 ) f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 J
2. Alcohol consumption (AC): alcohol, g/day	High Medium	Men (over 150)	f ( x ) = 0; x < 150 r, x 11 fx — 200 ) f ( x ) = —+ —* cos ------ , 150 < x < 200 22 ( 50 J
	High Medium	Women (over 100)	f ( x ) = 0; x < 100 „ ₄ 11 f x — 150 ) f ( x ) = —+ —* cos ------ , 100 < x < 150 2 2 ( 50 J
	Low High	Men (75-150)	f ( x ) = 0; x < 75 r, x 11 fx — 112.5 ) f ( x ) = —+ —* cos -------- , 75 < x < 112.5 2 2 ( 37.5 J 1 1 x — 150 f ( x ) =---* cos 11 , 112.5 < x < 150 2 2 ( 37.5 J f ( x ) = 0; x > 150
	Low High	Women (50-100)	g ( x ) = 0; x < 50 , x 11 f x — 75) „ g ( x ) = —+—* cos ----- , 50 < x < 75 22 ( 25 J , _x 11 f x — 100 ) g ( x ) =---* cos ------- , 75 < x < 100 2 2 ( 25 J g ( x ) = 0; x > 100
	Medium	Men (0-75)	f ( x ) = 0; x > 75 r, x 11 fx — 75) „ f ( x ) =---* cos ------ , 0 < x < 75 2 2 ( 75 J
	Medium	Women (0-50)	g ( x ) = 0; x > 50 / x 11 f x — 50) g ( x ) =---* cos ------ , 0 < x < 50 22 ( 50 J
3. Hypodynamia (GD)	High	Less than 5000 steps (7-10)	f ( x ) = 0; x < 1 r, x 11 f x — 10) „ , f ( x ) = —+ —* cos ----- , 7 < x < 10 2 2 ( 3 J

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Medium	5000 to 10000 steps (4-6)	f ( x ) = 0; x < 4 „ x 11. Г x - 5 ) - , _ f ( x ) = —+ —* cos ---- , 4 < x < 5 2 2 ( 1 ) 11 Г x — 6 ^ f ( x ) =---* cos ----- , 5 < x < 6 2 2 I 1 J f ( x ) = 0; x > 6
	Low	More than 10000 steps (0-3)	f ( x ) = 0; x > 3 x 11 Г x — 3 ) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 J
4. Psychotraumatic factors (PF)	High	Unstable (7-10)	f ( x ) = 0; x < 7 r, x 11 Гx — 10 ) f ( x ) = —+ —* cos ----- , 7 < x < 10 2 2 ( 3 J
	Medium	Stress resistance (4-6)	f ( x ) = 0; x < 4 . 11 Г x — 5 ) f ( x ) = —+ —* cos ---- , 4 < x < 5 2 2 I 1 J . 11 Г x — 6 ^ f ( x ) =---* cos ----- , 5 < x < 6 2 2 I 1 J f ( x ) = 0; x > 6
	Low	No (0-3)	f ( x ) = 0; x > 3 x 11 Гx — 3 ) „ , f ( x ) =---* cos ----- , 0 < x < 3 2 2 ( 3 J
5. Genetic factors (GF): ACVA, MI, AF, AH, DM	Extremely high	Two parents and all siblings under 50 years old (10)	f ( x ) = 0; x < 10 _r, x 11 Гx — 10 ) f ( x ) = — + — * cos ----- , x > 10 2 2 ( 1 )
	Very high	Two parents and all sibs over 50 years old / One parent or one sibs under 50 years old (8-9)	f ( x ) = 0; x < 8 . 11 Г x — 9 ^ f ( x ) = — + — * cos ---- , 8 < x < 9 2 2 ( 1 ) f ( x ) = 0; x > 9
	High	Two parents or all siblings over 50 years of age (6-7)	f ( x ) = 0; x < 6 x 11 Гx — 7 ) f ( x ) = — + — * cos ---- , 6 < x < 7 2 2 ( 1 J f ( x ) = 0; x > 7
	Medium	One parent or one sibs under 50 (4-5)	f ( x ) = 0; x < 4 „ x 11. Гx — 4.5 ) _ , _ f ( x ) = —+ —* cos ------ , 4 < x < 4.5 2 2 ( 0.5 J x 11 Гx — 5 ) , f ( x ) =---* cos ----- , 4.5 < x < 5 22 ( 0.5 ) f ( x ) = 0; x > 5
	Low	One parent or one sibs over 50 years old (3-2)	f ( x ) = 0; x < 2 x 11 Гx — 3 ) „ , „ f ( x ) =---* cos ----- , 2 < x < 3 2 2 ( 1 ) f ( x ) = 0; x > 3

Linguistic variables, designation and dimension	Term sets	Value ranges	Membership functions
	Very low	No (1-0)	f ( x ) = 0; x > 1 x 11 (x - 1 ) „ , „ f ( x ) =---* cos ----- , 0 < x < 1 2 2 ( 1 )
Hazard class
1. Very high risk (VHR)
2. High risk (HR)
3. Medium risk (MR)
4. Low risk (LR)
5. No risk (NR)

Table 2

Examples of the most commonly used T- and S-norms

T ( a, b )		S ( a , b )		Parameters
min { a , b }		max { a , b }
a · b		a + b = a · b
max {0, a + b –1}		min {1, a + b }
	a , if b = 1 b , if a = 1 ^ 0, if a , b < 1	■	a , if b = 0 b , if a = 0 0, if a , b > 0
ab max { a , b , y }		(1 - a )(1 - b ) min { (1 - a ),(1 - b ), y }		γ ∊ [0, 1]
ab Y + (1 -y )( a + b - ab )		a + b - (2 -y ) ab Y- (1 -Y ) ab		γ > 0
1 if Y i +\| (- - iy+¥ - 1) ^y \| к a b J		1 ¹ 1 fl 1 Л Y 1 (1 - 1) - ^Y+ (1 - 1) - ^Y\| к a b J		γ > 0
[ I	1 1 ^{1 1} ¥ ! ----1 a ^Y b ^Y J	1-- ¹—1 Г 1 1 ¥y + 1 к (1 - a ) ^Y (1 - b ) ^Y J		γ > 1
1 - ( (1 - a )^Y + (1 - b ) ^Y- (1 - a ) ^Y (1 - b ) ^y ) ^y		( a ^Y+ b ^Y- a^Y b ^y)^y		γ > 0
max { 0,1 - ( (1 - a ) y + (1 - b ) y ) ^Y j		min { 1,( a . + b ) 1 }		γ ≥ 0
, Г, ( Y ^a - 1)( Y b - 1) ) ^lo g y I ¹ ⁺ , 1 к Y- 1 J		Г Y ¹ - ^a Y ¹ - ^b к ^{1 lo} g y I ¹ ⁺ 1 к Y- 1 J		0 ≤ γ <1
max {0, (γ – 1)( a + b ) – 1 – γ ab }		min {1, a + b + γ ab }		γ > –1

Linguistic variables made it possible to build a logical-linguistic model, represented by a set of rules, a fragment of which is presented below:

IF A is Extremely high AND G is High AND BMI is High AND W is High AND LDL is High AND TG is High AND HbA 1c is High AND GFR is High AND DLV is High AND LAS is High AND LFEV is High AND SBP is High AND P is High AND DM is Very high AND AG is Very high AND AF is High AND MI is High AND ACVA is Very high AND S is High AND AC is High AND GD is High AND PF is High AND GF is Extremely high THEN VHR

IF A is Very high AND G is High AND BMI is High AND W is High AND LDL is High AND TG is High AND HbA 1c is High AND GFR is High AND DLV is Big AND LAS is High AND LFEV is High AND SBP is High AND P is High AND DM is High AND AG is High AND AF is High AND MI is High AND ACVA is High AND S is High AND AC is High AND GD is High AND PF is Low AND GF is Very high THEN VHR

IF A is Medium AND G is Low AND BMI is Medium AND W is Low AND LDL is High AND TG is Medium AND HbA 1c is Low AND GFR is Low AND DLV is Low AND LAS is Low AND LFEV is Low AND SBP is High AND P is Low AND DM is Low AND AG is Low AND AF is Low AND MI is High AND ACVA is Low AND S is Low AND AC is Low AND GD is Low AND PF is Low AND GF is Low THEN VHR

IF A is High AND G is High AND BMI is Medium AND W is High AND LDL is High AND TG is High AND HbA 1c is High AND GFR is High AND DLV is Big AND LAS is High AND LFEV is High AND SBP

is High AND P is Medium AND DM is High AND AG is Medium AND AF is High AND MI is High AND ACVA is High AND S is High AND AC is High AND GD is High AND PF is Low AND GF is High THEN HR

IF A is High AND G is High AND BMI is Medium AND W is High AND LDL is Medium AND TG is Medium AND HbA 1c is Medium AND GFR is Medium AND DLV is Big AND LAS is High AND LFEV is Medium AND SBP is Medium AND P is Medium AND SD is Medium AND AG is Medium AND AF is Medium AND MI is High AND ACVA is Medium AND S is Medium AND AC is Medium AND GD is Medium AND PF is Medium AND GF is Medium THEN HR

IF A is Medium AND G is Low AND BMI is Medium AND W is High AND LDL is Medium AND TG is Medium AND HbA_1c is Medium AND GFR is Medium AND DLV is Low AND LAS is High AND LFEV is Medium AND SBP is Medium AND P is Medium AND DM is Medium AND AG is Medium AND AF is Medium AND MI is Medium AND ACVA is Medium AND S is Medium AND AC is Medium AND GD is Medium AND PF is Medium AND GF is Medium THEN MR

IF A is Low AND G is Low AND BMI is Low AND W is Low AND LDL is Low AND TG is Low AND HbA 1c is Low AND GFR is Low AND DLV is Low AND LAS is Low AND LFEV is Low AND SBP is Low AND P is Low AND DM is Low AND AG is Low AND AF is Low AND MI is Low AND ACVA is Low AND S is Low AND AC is Low AND GD is Low AND PF is Low AND GF is Low THEN LR

IF A is Very low AND G is Low AND BMI is Low AND W is Low AND LDL is Low AND TG is Low AND HbA 1c is Low AND GFR is Low AND DLV is Low AND LAS is Low AND LFEV is Low AND SBP is Low AND P is Low AND DM is Low AND AG is Low AND AF is Low AND MI is Low AND ACVA is Low AND S is Low AND AC is Low AND GD is Low AND PF is Low AND GF is Very low THEN NR

Simulation studies using the constructed logical-linguistic model were carried out using T- and S- norms, as shown in Table. 2.

In view of the fact that conducting simulation studies using the logical-linguistic model is a rather complex process, we will make the transition from a system of rules to a neural network [17]. The structure of

the resulting hybrid neuro-fuzzy classifier is shown in Fig. 1; when tuning it, the T- and S- norms were used, presented in Table 2.

Consider the content aspects of the selected layers

in Fig. 1 [18].

Layer 1 . Degrees of membership of input variables

to the fuzzy sets defined for them A_ij are formed at the

output of the elements of this layer:

Ц A ij ( X ij ) = cos

— ± —• cos

П •

x ij

-b-ij

b ij - a ij

where a_ij , b_ij are the parameters of the membership function.

The initial values of these parameters are set in such a way that the membership functions satisfy the properties of completeness, normality and convexity. The values of these parameters are adjusted during

the network training process based on the gradient method.

Layer 2. Each element of this layer is a fuzzy “I” neuron, the output signal of which represents the level of operation of a fuzzy rule relative to the categorized image.

Layers 3–4 . The elements of these layers are designed to weightedly sum the output values of the elements of the previous layer. Values at the outputs of Layer 4 elements are formed using activation functions of the sigmoid type. These outputs are interpreted as the degree of membership of the presented object to the corresponding class.

A given system of fuzzy rules allows you to get training images. The output of the i -th element of the hidden layer of the network is calculated as follows:

O ki = f E W ij A kj ’

and the output layer element generates a value

O ki = f E V i A ki I,

where f ( z ) is unipolar transfer function, e.g. f ( z ) = ((1)/1 + exp(–z)); W_ij , V_i are fuzzy weights of the elements of the hidden and output layers, respectively; A_kj is fuzzy input.

Of particular importance are the issues related to the choice of T- and S- norms according to Table 1, the optimal choice of which allows you to reduce the time for setting up a neural fuzzy network and, as a consequence, to increase the efficiency of the classifier.

Algorithm for setting a neuro-fuzzy classifier

The fuzzy outputs of each network element are calculated as sets of α-levels relative to fuzzy inputs and weights.

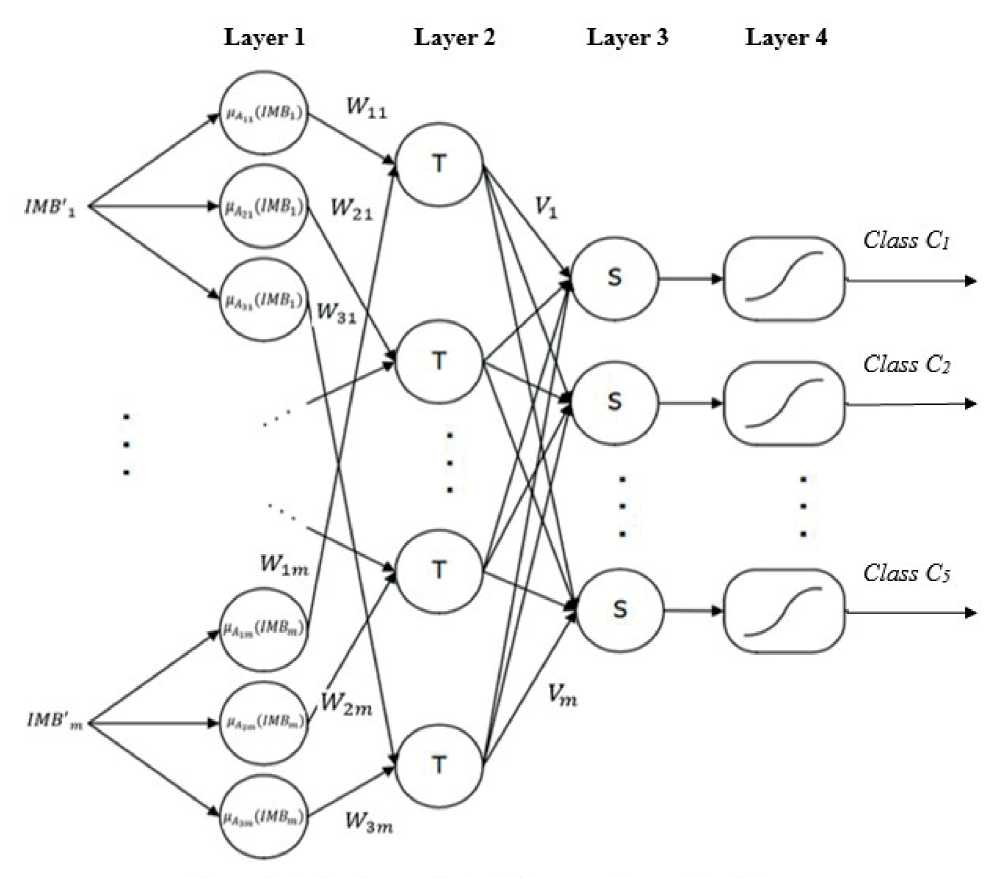
Figure 1. Structure of hybrid neuro-fuzzy classifier

Let us denote the sets of α-levels of the calculated output of the O_k , the target output of the B_k , the weights of the output element of the V_i and the weights of the elements of the hidden layer of the W_ij respectively as

[ O k ]^a = O k (a), O k (a), [ B k ]^a = B k (a), B R (a), [ V T = V i ^L (a), V R (a), [ W j ]^a = W j (a), W R (a), для ae[0,1], i = 1,..., r , j = 1,..., m .

From symmetry of W_ij and V_i is follow that

w(1) + 1V(3) (1)(3)

2) _ w j ⁺ w j „,(2) _ v i ⁺ v i

Wij =------------, v = j 22

i = 1, …, r , j =1, …, m .

The change in weights relative to the objective function of the s k (a) is formed as follows:

A w ⁽¹⁾( t ) = -n

Since the function f is strictly monotonically increasing, the following expressions are valid:

[ O k ]^a =

r f XVO

1 a

A w ⁽³⁾( t ) = -n

dsp (a) dwij1’ dsp (a) dwij3>

+ pA w^ -1),

+ PA wf ( t -1),

rr fl XVA. J (a) I, fl XVOki J (a)

V i=i У V i=i where

[ O ki ]^a

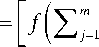
W ij A kj

f ( X m J W W ^L (a) ) , f ( X m WA j ] R (a) )

The minimized target function is defined for each set of a-level as follows: sk (a) := sL (a) + sL (a), где sL (a) = 2 (BL (a) - Ok (a))2, sR (a) = 2(BR (a) - OR (a))2, i.e. sL (a) denotes an error between the left boundaries of sets of α-levels of the target and calculated output values, and sR (a) denotes an error between the right boundaries of sets of α-levels of the target and calculated output values.

Next, the error function for the k- th training image is formed:

s k = X as k (a). a

This makes it possible to build a network training algorithm of this type for the error function s _k (a).

Assuming that the fuzzy weights of the neurons of the hidden layer have a symmetrical triangular shape, they can be represented by three parameters W j = w j ’ , w j , w ,j ³⁾, defining the left border, center and right border, respectively W_ij . Similarly, the fuzzy weights of the output neuron can be represented by the following three parameters V = v i ⁽¹⁾ , v ⁽²⁾ , v ⁽³⁾ , defining the left border, center and right border, respectively, V_i .

where η is coefficient that sets the speed of learning; β is pulse constant; t is index that characterizes the current point in time; j = 1, …, m .

Fuzzy weights W y = w ^ j ¹’, w ij ²⁾, w ij³⁾ are changed according to the rules:

w(j1) (t +1) = w^j1* (t) + A wj (t), wj (t +1) = wj (t) + Awj (t), w,y.(, + 1) = wjWwjM.

^j 2

Fuzzy weights V = v i ⁽¹⁾ , v ⁽²⁾ , v ⁽³⁾ are changed according to the rules:

v(1)(t +1) = v(1)( t) + A v(1)( t), v^(t +1) = v(3)( t) + A v(3)( t), v».( t+1) = v^t >+v!31' t >.

After weight change W_ij in the event that its left border becomes larger than the right one, we use simple heuristic rules:

wi(j1)(t +1) := min {w,j1)(t +1), w,(j3)(t +1)}, wij3) (t +1) := max { wij1* (t +1), w^ (t +1)}.

Similar heuristics are used for scales :

v ^ ¹ ’ ( t +1) := min { v ^ ¹ ’ ( t +1), v ( ³⁾ ( t +1) } ,

v ⁽³⁾ ( t +1) := max { v ⁽¹⁾ ( t +1), v ⁽³⁾ ( t +1) } .

The above steps are performed for all k = 1, ..., n training images: {( A 1 B 1 ), …, ( A n B n )}, где A k = ( A k 1 , …, A_k _m). It is also believed that p values of sets of α-levels are used to train a neural fuzzy network.

Thus, the algorithm for training a neuro-fuzzy network classifier is as follows:

Input: Initialization of fuzzy weights of network elements, current error E = 0, threshold value Emax; α = α1, α2, …, αi; n k = 1;

do while ( k < n )

i = 1;

do while ( i < n )

α = a i ;

E = 0;

do while E > E max

V A ki ;

O_k є neural.network(α);

E + E 1 ;

neural.network(α) є neural.network( ε_k (α));

end while;

i ++;

end while;

k ++;

end while.

Algorithm testing . To verify the correctness of the developed model, we examined 60 clinical cases (18 men and 42 women). Due to the specifics of the medical institution on the basis of which the study was conducted, as well as due to certain social patterns, older patients predominate in the sample. In accordance with the proposed indicators, the model assesses their hazard class for CVD risk factors.

Statistical analysis. Statistical data processing was carried out using Microsoft Office Excel and Statistica 6.1 software. Due to the unknown type of sample distribution, the Bernoulli distribution was used. When testing hypotheses, the results were considered statistically significant at p < 0.05.

The work carried out complies with the ethical standards of the Declaration of Helsinki (2013) and the Rules of Good Clinical Practice , approved by the Order of the Ministry of Health of the Russian Federation dated 01.04.2016, No. 200n.

Results and discussion

After training using data from clinical practice, a neuro-fuzzy classifier is used to solve the classification problem. For the hazard class “Very High Risk”, 24 clinical studies were conducted for female patients of the “Extremely High (70+)” age group. The neural network incorrectly detected the risk of CVD in 4 cases; the correct answers were in 20 cases.

These results made it possible to put forward the following hypotheses:

Basic hypothesis: H ₀ = p ₀ = 0.05 – results are incorrectly defined.

Alternative hypothesis: H ₁: p ₁ > 0.05

Sequence n = 24 independent observations xⁿ Bernoulli X ≈ B ( p ): the correct definition is the correct answer, all other outcomes are the wrong answer. The criterion for testing the basic hypothesis was based on observations of the total number of correct answers

S . This random variable S has a binomial distribution

S ≈ B ( N ; p ), N = 24. With some tolerances (at p₀ = 0.05, the random variable has a symmetric distribution) S can be approximated by a normally distributed random variable. When testing the basic hypothesis H ₀, p ₀ = 0.05, let’s introduce a standardized random variable

T — T CT ( X n ) =

S - M [ S ]

= S

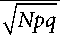
— z 0 ,

having approximately standard normal distribution N (0; 1). Then the critical area К _α hypothesis deviations H ₀

with the level of significance of the error α = 0.05 equal:

K a — { T :| T |> z 24;0.05 — -1.71}.

Observed value of the criterion

• i ааё

4 - 24 * 0.05

V24 * 0.95 * 0.05

— 2.64 > Z 24;0.95

-1.71

does not fall into the critical area К_α .

Thus, H ₀: p ₀ = 0.95 not rejected ( α = 0.05) against the background of an alternative hypothesis H ₁: p ₁< 0.95. According to the results of the study with the permissible level of significance of errors of the first kind α = 0.05 the risk is defined correctly.

Similar calculations were performed for all other age groups of patients belonging to each risk class. For the female, the results presented in tables 3–5 were obtained. According to the results of clinical studies with an acceptable level of significance of the error of the first kind of 0.05, the risk is determined correctly. Due to the peculiarities of the study, there are practically no patients whose age group we have defined as “low” or “very low”. Therefore, there are no age group data in the results presented in the tables.

When conducting similar calculations for male patients, the results presented in Table were obtained. 6–8. According to the results of clinical studies with an acceptable level of significance of the error of the first kind of 0.05, the risk is determined correctly.

Table 3

Compliance with the Hazard Class “Very High Risk” (VHR) of female patients

Age group	Total number of patients	Very high risk (VHR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	25	24	20	4
Very high (60-69)	10	9	7	2
High (50-59)	4	4	2	2
Medium (40-49)	3	0	0	0

Table 4

Compliance with the hazard class “High Risk” (HR) of female patients

Age group	Total number of patients	High risk (HR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	25	4	3	1
Very high (60-69)	10	3	1	2
High (50-59)	4	0	0	1
Medium (40-49)	3	1	1	0

Table 5

Compliance with the hazard class “Medium risk” (MR) of female patients

Age group	Total number of patients	Medium risk (MR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	25	3	2	1
Very high (60-69)	10	2	2	0
High (50-59)	4	4	2	2
Medium (40-49)	3	3	2	1

Table 6

Compliance with the Hazard Class “Very High Risk” (VHR) of male patients

Age group	Total number of patients	Very high risk (VHR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	6	6	5	1
Very high (60-69)	5	4	3	1

Age group	Total number of patients	Very high risk (VHR)	Number of correctly defined	Number of erroneously defined
High (50-59)	3	3	1	2
Medium (40-49)	4	1	1	0

Table 7

Compliance with the hazard class “High Risk” (HR) of male patients

Age group	Total number of patients	High risk (HR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	6	3	1	2
Very high (60-69)	5	3	2	1
High (50-59)	3	1	0	1
Medium (40-49)	4	2	2	0

Table 8

Compliance with the hazard class “Medium risk” (MR) of male patients

Age group	Total number of patients	Medium risk (MR)	Number of correctly defined	Number of erroneously defined
Extremely high (70+)	6	1	0	1
Very high (60-69)	5	2	0	2
High (50-59)	3	2	2	0
Medium (40-49)	4	2	1	1

Conclusion

Analysis of the test results, built neuro-fuzzy classifier, allows us to conclude about its satisfactory operation even when using incomplete information, which makes it possible to use it for prompt decision-making [19-21].

The constructed neuro-fuzzy classifier is designed to assess cardiovascular risk and allows specialist doctors in clinical practice to quickly assess the risks of CVR and make appropriate decisions even in the case of an incomplete set of input data. In the future, it is possible to expand the constructed neuro-fuzzy classifier by including additional relevant indicators, for example, characterizing the effect of coronavirus infection on CVD.

The factors influencing the risks of cardiovascular diseases are highlighted. Appropriate linguistic variables have been introduced for these indicators. Unlike the existing scales, additional indicators available in the national recommendations are introduced into the neuro-fuzzy classifier. A logical-linguistic model was constructed, from which the transition to a hybrid neuro-fuzzy classifier was carried out, which made it possible to assess the influence of the selected factors on the risks of cardiovascular diseases, which was tested on clinical examples.

As a result of approbation of the proposed intellectual digitalization of the risks of the cardiovascular system on the example of clinical observations, the risk of cardiovascular events is determined correctly, which allows us to talk about the prospects for introducing this model into clinical practice and guarantees doctors a more accurate diagnosis and optimization of activities.

Statement on ethical issues

Research involving people and/or animals is in full compliance with current national and international ethical standards.

Conflict of interest

None declared.

Author contributions

The authors read the ICMJE criteria for authorship and approved the final manuscript.

Список литературы Intelligent digitalization of cardiovascular risks

World Health Organization. Cardiovascular diseases. URL: https://www.who.int/cardiovascular_diseases/about_cvd/ru/. (In Russ.).
Strong K, Mathers C, Epping-Jordan J, Beaglehole R. Preventing chronic disease: a priority for global health. International Journal of Epidemiology. Apr 2006; 35(2): 492-494.
Epping-Jordan JE et al. Preparing the 21st century global healthcare workforce. BMJ. 2005 Mar 19; 330(7492): 637-639.
Sergienko IV, Shestakova MV, Boytsov SA. «Extreme risk category in the system of stratification of cardiovascular complications» Consensus of the Council of Experts «National Society of Atherosclerosis», Non-governmental organization «Russian Association of Endocrinologists», «National League of Cardiogenetics», Russian Society of Cardiology, 2018: 15-26. (In Russ.).
Oganov RG, Kontsevaya AV, Kalinina AM. Economic damage from cardiovascular diseases in the Russian Federation. Cardiovascular therapy and prevention. 2011; 10 (4): 4-9. (In Russ.).
Mortality trends in Russia at the beginning of the XXI century (according to official statistics). Cardiovascular therapy and prevention. 2011, 10 (6): 5–10). (In Russ.).
National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III). Third Report of the National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III) final report. Circulation, 2002. Vol. 106, No. 25, pp. 3143–3421. PMID 12485966.
Conroy RM, et al. SCORE project group. Estimation of ten-year risk of fatal cardiovascular disease inEurope: the SCORE project. Eur Heart J.: 2003, Vol. 24, No. 11, pp. 987–1003. PMID 12788299.
Graham I, et al. European guidelines on cardiovascular disease prevention in clinical practice: full text. Fourth Joint Task Force of the European Society of Cardiology and other societies on cardiovascular disease prevention in clinical practice. Eur J Cardiovasc Prev Rehabil: 2007. Vol. 14, No. Suppl 2, pp. S1–113. PMID 17726407.
ESC/EAS Recommendations for dyslipidemia Treatment: Lipid Modification to Reduce Cardiovascular Risk 2019. Russian Journal of Cardiology. 2020; 25(5): 3826. DOI: 10.15829/1560-4071-2020-3826 (In Russ.).
Arnett DK, Blumenthal RS, Albert MA, et al. Guideline on the Primary Prevention of Cardiovascular Disease: Executive Summary. 2019 ACC/AHA.Journal of the American College of Cardiology.2019, 26028. DOI: 10.1016/j.jacc.2019.03.009.
Tuomilehto J. Identification of people at high risk for CVD or diabetes. University of Helsinki, Finland, 2020.
EASD, ESC Recommendations for Diabetes, Prediabetes and COVD: European Society of Cardiology (ESC), European Association for the Study of Diabetes (EASD), 2014. (In Russ.).
Zhou F, Yu T, Du R, et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohortstudy. Lancet, 2020; 395:1054-1062.
Sisti N, Valente S, Mandoli GE, et al. COVID-19 in patients with heart failure: the new and the old epidemic. Postgraduate Medical Journal, 2021; 97: 175-179.
URL: https://www.heart.org/en/news/2020/09/03/what-covid-19-is-doing-to-the-heart-even-after-recovery.
Kofman A. Introduction to the theory of fuzzy sets. Moscow, Radio i swyaz, 1982. (In Russ.).
Borisov VV, Kruglov VV, Fedulov AS. Fuzzy models and networks. Moscow, Goryachaya liniya-Telekom, 2012, pp. 182-185. (In Russ.).
Filippov YuA, Korpan NN, Tyutyunnik VM. Technologies for determining the functional and physiological state of a person. Bulletin of the Russian New University. Ser.: Complex systems: models, analysis, control. 2020;5:63-71. DOI: 10.25586/RNU.V9187.20.05.P.063. (In Russ.).
Tyutyunnik VM. Thermodynamics of irreversible processes and self-organization in information flows. International Journal of Advanced Research in IT and Engineering. 2019;8(3):18-24.
Tyutyunnik, VM. The Nobel Congress has completed its work in Tambov. Cardiometry. 2019; November, 15:73-77.

Еще

Статья научная