Инженерный метод преследования-уклонения объектов для задач адаптивного управления роботами совместного использования

В результате успешных внедрений робототехники в промышленные и специальные области, совершенствования управляющих и сенсорных систем роботов, систем их адаптивного программирования, становлению и развитию возможностей методов на основе искусственного интеллекта появился новый класс роботов, называемый роботами совместного использования, или сокращенно, коботами. Коботы проникают в области, в том числе непроизводственные, где требуется более гибкое функциональное взаимодействие с человеком, которое сложно или попросту невозможно осуществить на основе жесткого программирования робототехнических систем. Такое взаимодействие может иметь место при работах человека и кобота с объектами на общем транспортере, при обращениях к общему контейнеру-накопителю, при маркировочных разгрузочно-погрузочных или складских работах, при выполнении смешаной последовательности операций, часть из которых, особенно сложных с точки зрения манипуляций, выполняет человек (например, в лабораториях химико-биологического анализа), при работах по ассистированию человека в медицинской деятельности и т.д. [1–4].

В робототехнологических комплексах на основе коботов существует единое/общее рабочее пространство человека и робота, не разграниченное периметрами безопасности или защитными ограждениями. Это приводит к особенному требованию, а именно – безопасности для человека действий робота в этом пространстве на основе дополнительного функционала автоматической адаптации движений или их останова, а также ограничения их мощности. Удовлетворение этого требования возможно только на основе новых научных, практикоориентированных разработок по совершенствованию алгоритмов адаптивного управления роботами на основе внедрения мультисенсорной информации, оперативной и/или обучающей [5–11].

• 1.    Описание исследуемого вопроса

При построении алгоритмов управления роботами совместного использования могут оказаться инструментально полезными решения задач взаимного движения двух материальных точек A и B в следующих условиях: наблюдаемое движение точки A является задающим, а движение точки B является вынужденным движением в соответствии с некоторым критерием, налагаемым на взаимное расположение точек. При этом управление радиус-вектором rb точки B в неподвижной декартовой системе OXY Z производится изменением обобщенных координат q G R3x1 согласно уравнению:

d r b ( t ) dt

= r b ( t ) = Jq ( t ))q( t ) ,

где J G R ^3x3 - ограниченная невырожденная матрица с действительными коэффициентами, t – время.

В зависимости от поставленного критерия задачи совместного движения могут существенно различаться, но распространенной является задача ≪ преследования-уклонения ≫ объектов. В общетеоретическом (математическом) смысле эта задача достаточно исследована, и для нее предложены определенные решения [12–14]. Метод, рассматриваемый в данной статье, имеет практическую направленность и адресован именно роботам-манипуляторам, как инженерный, т.е. не требующий сложной вычислительной адаптации теоретических заключений. Однако, теоретические перспективы метода существуют и связаны, прежде всего, с задачами интегрирования вращательных движений в механических системах, в том числе, с кинематической избыточностью.

1.1.    Постановка задачи 1 (задача преследования)

Движение точки A (радиус-вектор точки обозначим r _a ) происходит по априорно неизвестному для точки B закону с ограниченной скоростью ||r_a ||, но функция ошибки e ( t ) = r _a ( t ) — r b ( t ) , а также ее производная по времени e ( t ) доступны мгновенному измерению, при этом вторая производная e ( t ) существует. Начальное положение точки B относительно точки A принадлежит обозримой сфере некоторого радиуса S .

Требуется построить управление движением точки B такое, что с течением времени модуль вектора ошибки расположения точек устойчиво попадает в трубку достаточно малого радиуса ε (радиус захвата цели).

Упростим задачу допущением того, что каждое обобщенное ускорение q i , i = 1 , 2 , 3 может быть получено запрашиваемой (требуемой) величины, т.е. что мощность движения точки B достаточно большая. Последнее, разумеется, имеет смысл только в случае наличия ненулевой массы точки B.

1.1.1.    Решение задачи преследования

Продифференцировав уравнение

J ^{1 (} q ^{( t ))} r ь ^(t) = ^{q ( t )} ,

получим закон изменения обобщенных ускорений, соответствующий движению r _a ( t ) (зависимость величин от времени опустим для сокращения записи):

^q = ^{J 1 (} q ⁾⁽ r a ^{— e )}+ d JJ ¹ ^ ⁽ r a ^{— e )} -                    ⁽³⁾

Закон управления ошибкой e ( t ) , обеспечивающий решение (3), зададим в виде уравнения собственного движения устойчивого колебательного звена (4):

e + k 1 e + k ₂ e = 0 , k 1 = 2 vA, k ₂ = A ² , 0 < v <  1 .                    (4)

С учетом (4) преобразуем (3) к виду:

q = J 1 ( q ) ( Г а + k i e + k 2 e ) + d J J 1 ( q )^ ( r a — e).

(5)

Параметром настройки движения точки B в соответствии с (5) является λ – угловая частота свободных колебаний звена (4). Управление величиной λ построим из условия монотонного убывания функции ^(t) - угла между векторами скоростей точек ra(t) и rь(t), которое необходимо для астатизма удержания точки A в движении. Для этого потребуем выполнение условия d-(cos 0 (A(t))) > 0 dt

причем равенство достигается только при 0 = 0 .

Поскольку

_Q    r T ^Jq

C0S 0 = Hr JI||Jq II нетрудно установить на основании правила дифференцирования дроби, что (6) эквивалентно условию:

-d(rTJq)- (rTJq)-dOn(||rallllJqII)) > o. dtdt

Продифференцируем первое слагаемое, используя цепочку преобразований с учетом (5):

^r T ^Jq + ^r T J ^q + ^r T ^jq = ^r T JJ ^{1 ( r} a ^{- e )} + ^r T J J ^{1 ( r} a ^{- e )}+

+rTJJ-1(ra + k1 e + k2e) + rTJ dJJ-1) (ra - e) =

= ^r T ^{e X} 2 + ^{2 X r} T e + ^{2 r} T ^r a ^{- r} T e .

Здесь учтено, что

jj-1 + j (J. j-Л = A (jj-1) = dE = o, dt         dtdt где E – единичная матрица.

С учетом (8) выражение (7) запишем в виде неравенства:

mX ² + nX + p >  0 ,

где m = rTe, n = 2rTe, p = 2rTra - rTe - (rT J

Необходимым условием существования тривиального решения e (t) = 0 при управлении, заданным соотношениями (5) и (9) будет, как нетрудно заметить, неравенство:

^L(ra^(t)) = ²rTra ^{- (}rTra) d^(ln(|ra^||||JqII)) > ⁰-                       ⁽¹⁰⁾

Покажем, что неравенство (10) выполняется. Движение точки A будем рассматривать на последовательности достаточно малых интервалов времени (ti1; ti2], i = 1, 2,... c начальными условиями r_a(ti1), r_a(ti1) = Ri, на каждом из которых движение точки A можно рассматривать, как прямолинейное с вектором мгновенной скорости r_a(t) = Rie^a(t), где a(t) — некоторая дифференцируемая на (tn; ti2],i = 1, 2,... функция. Подставив это выражение в (10), получим непротиворечащее ему на каждом интервале равенство:

Li(ra(t)) = 2|R||²a(t)e^2a(t)- |R|²e^2a(t)d (ln (||Ri|²e^2a(t))) =

= 2|R||²а^)е^2а<^ - 2|R||²e^2a(t)d (In |R| + a(t)) = 0.

При анализе (9) рекомендуется учесть следующие замечания. Завышение величины λ приведет к увеличению требуемой мощности движения точки B, если бы речь шла о движении материального объекта, имеющего массу, на котором эта точка расположена. С другой стороны занижение λ приведет к большой ошибке в начале преследования, что существенно затруднило бы задачу, если бы опять же речь шла о движении технического объекта.

Поэтому нет сомнения, что управление величиной λ это весьма ответственный процесс, который, будучи успешным, приведет к эффективному, вплоть до робастного, управлению движением точки B в реальном мире. Результаты компьютерного моделирования, описанного ниже, позволяют утверждать, что весьма эффективным решением для λ является следующее:

A =

| min (max ( k-n+mD Amin) ; Amax) , если m > 0 П D > 0, (^                   ^A0 ⁼const € [Amin; Amax] ,

где D = n²— 4mp, 0 < A_mi_n< A_max- постоянные границы некоторого интервала, k = const. Значения постоянных λ_mi_n , λ_max , λ0 , k подбираются в процессе вычислительного эксперимента.

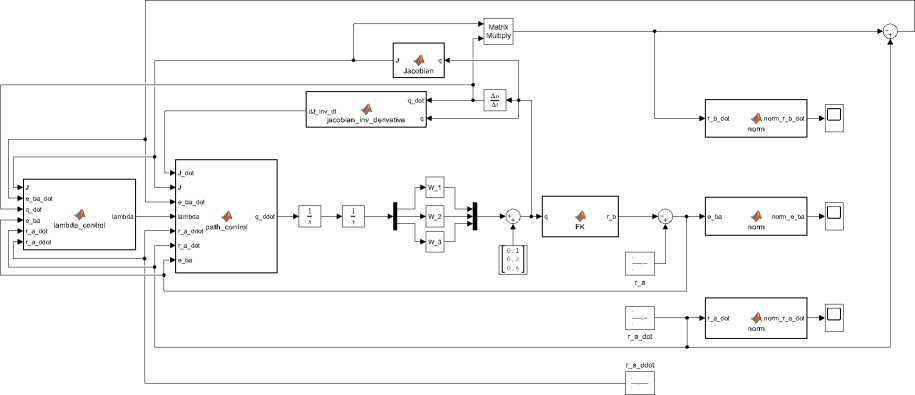
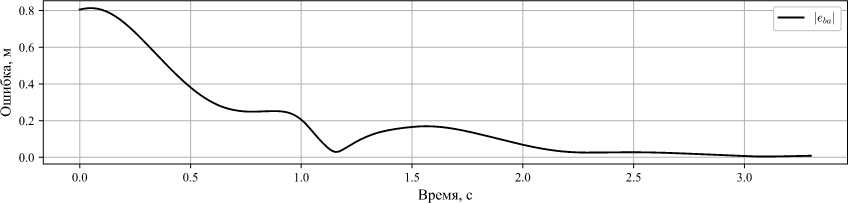
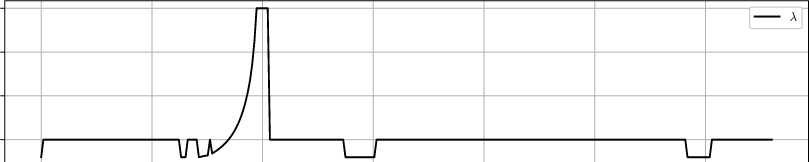
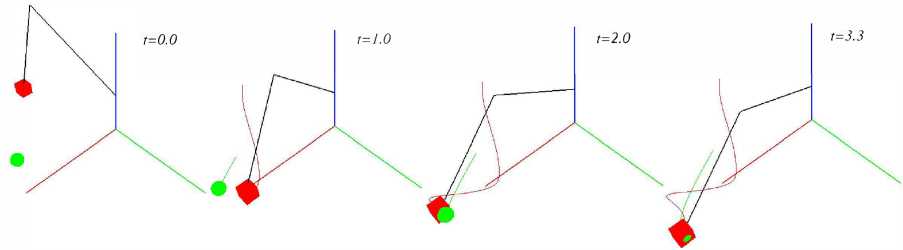
1.1.2.    Численное моделирование. Анализ результатов

Моделирование проводилось для ситуации, когда под точкой понимался полюс эффектора (концевого звена) манипулятора с кинематической схемой и геометрическими параметрами транспортных степеней подвижности робота KUKA KR-30-3 [15]. При этом точка A понималась как точка некоторого объекта работы. Моделируемая ситуация возникает, например, при захватах роботом объектов, движущихся на ленте транспортера.

Привод робота представляет собой следящий трехконтурный привод на основе двигателя постоянного тока, замкнутый по положению при настройке на оптимум по модулю в рамках принципа подчиненного регулирования контуров [16]. Известно, что при этом привод может быть описан передаточной функцией эквивалентного колебательного звена:

,           К

W (s) = ^й^ТТГ’                  (12)

T ²s² + 2ET s + 1

где T – постоянная времени, E – коэффициент демпфирования, K – коэффициент усиления, s – переменная в преобразовании Лапласа.

Для моделирования системы трех приводов был использован, как наиболее неблагоприятный для получения желаемого результата, принцип самого медленного звена, когда передаточные функции всех приводов принимаются равными функции самого медленного из них. При этом постоянная времени T считалась неизменной при движениях звеньев робота, что справедливо при наличии в приводах редукторов с большими передаточными отношениями, при которых взаимовлиянием звеньев допустимо пренебречь [17].

Блок-схема системы, управляемой по описанному алгоритму, представлена на рис. 1, на котором введены следующие обозначения:

• •    ≪path_control≫ – блок расчета обобщенных ускорений;

• •    ≪Jacobian≫ и ≪jacobian_int_derivative≫ – блоки расчета якобиана и производной по времени его обратной величины для трех первых звеньев робота KUKA KR-30-3 с учетом их геометрических параметров;

• •    ≪Matrix Multiply≫ – блок умножения матриц;

• •    ≪FK≫ блок решения прямой задачи кинематики;

• •    ≪lambda_control≫ – блок расчета λ в соответствии с формулой (11);

• •    ≪norm≫ – блок вычисления модуля вектора входных сигналов;

• •    W_1,W_2,W_3 - блоки моделирования влияния динамических свойств приводов на отработку задания по обобщенным координатам, описываемых соотношением (12).

Ниже представлены значения параметров компьютерной модели рассматриваемой задачи:

T = 0, 18, E = 0, 55, Amin = 3, Amax = 15, Ao = 5, K = 1, k = 1,2.

Также были предъявлены требования к значению радиуса захвата цели: е < 4 мм.

Для проведения вычислительных экспериментов была разработана программная реализация на языке Python, воспроизводящая описанную логику управления. С целью расширения возможностей анализа динамики работы системы в программный код была интегрирована функция визуализации библиотеки Pygame+OpenGL. Реализация проводилась с применением современных инструментов и методологий программирования, обеспечивающих высокую точность и наглядность результатов. Численные оценки матриц Якоби, ее пр                                                                               и по

Рис. 1. Блок-схема управления движением преследования

Данный подход позволяет не только верифицировать корректность работы системы управления, но и проводить детальный анализ ее поведения в различных режимах, что соответствует требованиям, предъявляемым к исследованиям в данной предметной области.

На рис. 2 показаны результаты эксперимента, который проводился с произвольным выбором начального положения эффектора робота при траектории движения точки A, задаваемой следующими уравнениями:

'xa(t) = 0, 5 sin(0,5t) + 1, ⁽ ya(t) = 0, 5sin(0, 3t),

^О = 0,4.

Радиус захвата цели составил е = 0, 004 м при начальном расстоянии между точками го = 0, 8 м.

На рис. 3 представлены положения моделируемых объектов в фиксированные последовательные моменты времени, на которых точки A показана синим цветом, а точки B – красным; показаны траектории движения точек. Оси системы координат обозначены цветом: ось Z – синим цветом, OY – зеленым, OX – красным.

Результаты моделирования также позволили определить предельное значение г скорости движения точки A, обуславливающее снижение эффективности алгоритма для динамики приводов, определяемой постоянной времени T > 0,18 с, что совершенно закономерно для инерционных систем. В данном случае предельное значение скорости r'i = 1, 5 м/с, после которого наблюдается существенный рост радиуса захвата цели.

1.2.    Постановка задачи 2 (задача уклонения)

Точка A начинает быстрое движение в неподвижную позицию P , в которой в данный момент находится точки B, провоцируя столкновение с ней ударом, при этом с изменением положения точки B движение точки A не меняется. Под столкновением точек будем понимать ситуацию, когда при некотором назначенном расстоянии разделения точек d наступит момент времени t_d такой, что выполнится условие:

lira(td) - rb(td)H                                         (13)

Момент времени, когда точки A попадает в P , обозначим t_a.

a)

0.0                    0.5                    1.0                    1.5                    2.0                    2.5                    3.0

Время, с

в)

0.0                    0.5                    1.0                    1.5                    2.0                    2.5                    3.0

Время, с

Рис. 2. Графики модулей векторов скорости точек объектов а), расстояния между объектами б), значения параметра λ настройки алгоритма преследования в)

Рис. 3. Положения точек объектов преследования в моменты времени ti

Требуется построить управление движением точки B такое, чтобы начиная с некоторого to при to < t < ta выполнялось условие:

lira^(t) - rb(t)|| = lira^(t0) - rp|| > d. ⁽¹⁴⁾

Таким образом, требуется избежать столкновения точек эквидистантным уклонением точки B. Для сформулированной таким образом задачи производственной ситуацией является та, при которой человек, находясь в одном рабочем пространстве с роботом, совершает случайное непреднамеренное движение в сторону эффектора робота, что угрожает травмой. Поэтому робот должен совершить адаптивное движение, чтобы избежать столкновения.

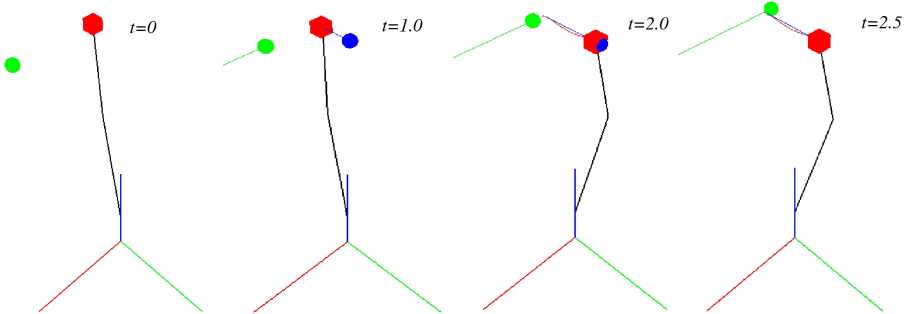
1.2.1.    Решение задачи уклонения

Будем придерживаться подхода, рассмотренного в предыдущем разделе. Считаем, что в перпендикулярном направлении к вектору r_a(to) — rp в горизонтальной плоскости OXY от P движется точки A^∗– целевая точка для преследования точкой B (мнимая цель). Положение точки A^∗(радиус-вектор обозначим r^∗_a) определим зависящим от положения точки A согласно формуле:

ra^(t) = rp + У HMM - rp 112 - lira^(t)- rpll^{2 u(t)},

ra^(t)- rp

u(t) = -——----- x v, v - орт оси OZ. Hra(t) — rp H

Таким образом, движение точки A генерирует движение мнимой цели A^∗, которую будет преследовать точки B при управлении согласно (5) и (9) и (11), вследствие чего произойдет уклонение от столкновения с A.

Заметим, что задача существенно бы усложнилась, если бы точки A, изменяя направление, перемещалась в позицию мгновенного (текущего) положения точки B, т.е. осуществляла бы преследование точки B. Но, поскольку для такой задачи трудно найти пример производственной ситуации, в данной статье эта задача не рассматривается.

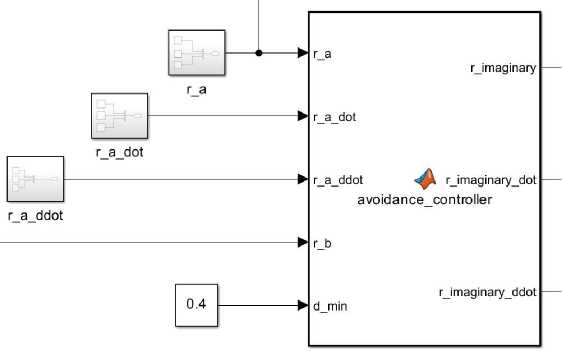
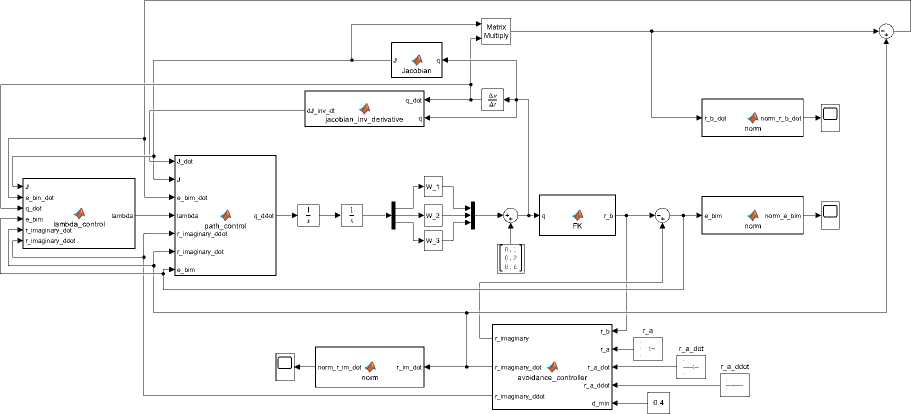
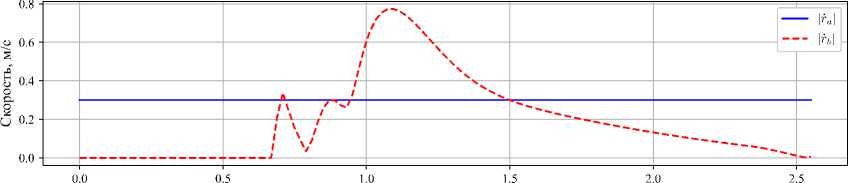
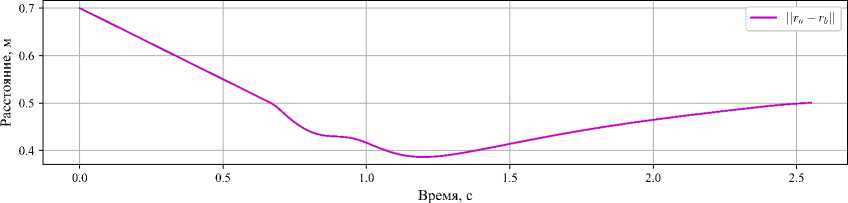
1.2.2.    Численное моделирование. Анализ результатов

В случае решения задачи уклонения были выбраные следующие модельные параметры:

T = 0,18, E = 0,55, Amin = 3, Amax = 15, Ao = 10, K = 1, k = 1,2.

Для реализации алгоритма уклонения на основе уже существующей схемы, приведенной на рис.1, необходимо добавить блок ≪avoidance_controller≫ , структурная схема которого представлена на рис. 4.

Рис. 4. Блок генерации движения мнимой цели

Он получает на вход данные о положении, скорости и ускорении точки A (r_a, r_a_dot, r_a_ddot), а также данные о положение эффектора (r_b) и радиус безопасного расстояния (d_min). Далее на основании этих данных блок формирует мнимую точку преследования для точки B, расположенной на эффекторе робота. Для этого на выходе блок ≪avoidance_controller≫ формирует положение, скорость и ускорение мнимой точки (r_imaginary, r_imaginary_dot, r_imaginary_ddot) соответственно. Эти данные поступают на вход схемы алгоритма преследования (см. рисунок 1) вместо r_a, r_a_dot, r_a_ddot. Конечная структурная схема представлена на рис. 5.

На рис. 6, 7 показаны результаты моделирования ситуации, когда точки A движется равномерно со скоростью 0, 3 м/с. При визуализации оси системы координат и точки B отмечены тем же цветом, что и в предыдущей задаче. Точка показана красным цветом, а мнимая цель - синим. Для выбранного значения безопасного расстояния dmin =0,4 ми постоянной времени приводов движения не быстрее 0,18 с критическая скорость точки A, после которой уклонение точки B не выполняется, составила f'i = 1, 05 м/с.

Рис. 5. Блок-схема алгоритма уклонения

Время, с

в)

Время, с

Рис. 6. Графики модулей векторов скорости точек объектов а), расстояния между объектами б), значения параметра А настройки алгоритма уклонения в)

Рис. 7. Положения точек объектов уклонения в моменты времени ti

Заключение

Рассмотрен инженерный метод решения задачи преследования-уклонения объектов в варианте движения материальных точек. При априорно неизвестном законе движения в пространстве ведущей точки управление ведомой точкой осуществляется по ускорению с переменными коэффициентами с однопараметрической настройкой. Предложено и обосновано правило настройки коэффициентов.

Построены математическая модель алгоритма управления и представлена программная реализация на языке Python с 3D-визуализацией результатов моделирования на примере роботехнической системы KUKA KR-30-3.

Установлено, что область устойчивости тривиального решения для величины ошибки положения точек существует в ограниченном интервале скоростей движения, что обсуслов-лено влиянием постоянных времени контуров положения исполнительного привода робота.

Работа проводилась при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект FSFS-2024-0012).