Искусственные молекулы, собранные из искусственных нейронов, воспроизводящих работу классических статистических критериев

Если речь идет о натурном эксперименте и получении реальных данных, практически всегда возникает проблема малых выборок. Биолог, подтвердивший свою гипотезу на 16 кроликах (морских свинках, лабораторных крысах или мышах) в глазах своих коллег будет выглядеть не убедительно. На столь малых выборках сегодня нельзя проверить даже гипотезу нормальности распределения данных статистическими критериями, созданными в прошлом веке. По стандартным рекомендациям [1] для доказательной проверки гипотезы нормальности с доверительной вероятностью 0.99 по хи -квадрат критерию потребуется выборка в 160 и более опытов.

То же самое относится и к иным не параметрическим статистическим критериям [2].

В качестве иллюстрации проблемы на рис. 1 приведены распределения нормальных и равномерных данных на выходе сумматора искусственного нейрона, воспроизводящего работу хи -квадрат критерия.

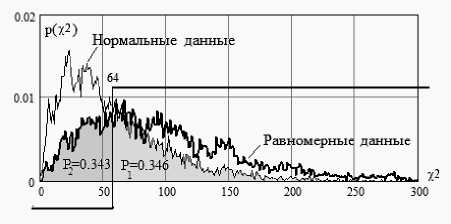
Рис. 1. Работа хи-квадрат нейрона, настроенного на разделение малых выборок в 16 опытов нормальных данных и данных с равномерным распределением (доверительная вероятность к решению - 0.66)

Совершенно иная ситуация сложилась в нейросетевой биометрии.

К результатам работы сети из 256 искусственных нейронов со стороны общества существует высокий уровень доверия. Автоматически обученная по ГОСТ Р 52633.5 [3] сеть искусственных нейронов на 16 примерах образа "Свой" узнает своего хозяина с доверительной вероятностью 0.99 и выявляет попытки предъявления случайных образов "Чужой" с доверительной вероятностью 0.99999. Все это является следствием огромного интереса к биометрии со стороны мирового сообщества, проявляемого в течении последние 30 лет.

Одним из корней доверия к новой технологии является ее высокий уровень стандартизации. Так, по классической статистике в России действует только две рекомендации [1, 2] и один стандарт по терминологии [4], а по биометрии введен в действие 51 стандарт. Формально уровень стандартизации биометрии по сравнению с уровнем стандартизации классической статистики в несколько раз выше.

Все это следствие того, что на биометрию ведущими в информационном отношении государствами (США, Евросоюз, Китай, Россия) за последние 30 лет были затрачены значительные материальные ресурсы. Вполне возможно, что ресурсов, потраченных на решение задач биометрии, за последние 30 лет было больше, чем ресурсов, потраченных мировым сообществом на создание критериев классической статистики за 120 лет ее развития. Пирсон создал хи -квадрат критерий в 1900 г., что можно считать началом интенсивного развития классической математической статистики.

Очевидно, что часть наработанных в нейросетевой биометрии и стандартизованных решений можно перенести в классическую статистику. Как показала практика, для каждого из примерно 200 известных статистических критериев [5] может быть построен эквивалентный искусственный нейрон, преобразующий континуум возможных входных состояний малой выборки в один разряд кода (рис. 2).

В итоге мы получаем некоторый статистический аналого-цифровой преобразователь, который можно рассматривать как искусственную статистическую молекулу [6, 7, 8, 9].

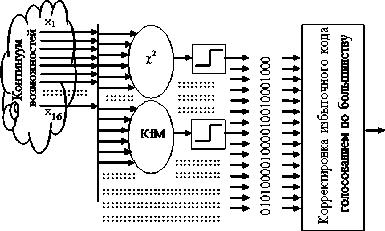
Рис. 2. Широкая нейронная сеть, состоящая из десятков или сотен нейронов, воспроизводящих работу статистических критериев (нейросетевая математическая молекула)

Право на такую интерпретацию нейросетевого статистического преобразования дает квантовая химия и квантовая физика, которые рассматривают естественные молекулы, преобразующие континуум собственной энтропии (собственной температуры) в выходные спектральные линии (в конечное число фотонов с дискретными значениями частоты). Нет формальной разницы между дискретными состояниями спектральных линий молекулы водорода и дискретных спектральных линий амплитуд вероятности появления выходных кодовых состояний нейросетевой статистической молекулы рис. 2.

Еще одной аналогией является то, что монография [5] содержит описание примерно 200 известных статистических критериев прошлого века. То есть длина выходного кода искусственной статистической молекулы (рис. 2) уже сегодня может составить порядка 200 бит. Перенос опыта нейросетевого анализа биометрии на решение задач классической статистики показал, что к классическим статистическим критериям могут быть добавлены десятки новых статистических нейросетевых критериев [10, 11, 12]. Можно предположить, что добавление новых статистических критериев позволит в ближайшее время увеличить выходную разрядность искусственных нейросетевых молекул до 256 бит, как это рекомендует пакет из семи национальных стандартов России по нейросетевой биометрии (номера стандартов - ГОСТ Р 52633.хх-20хх). Ориентация на действующие стандарты нейросетевой биометрии при создании нейросетевой статистики искусственных молекул - это попытка сократить достаточно сложный и тернистый путь завоевания доверия к уже отработанной вычислительной технологии в биометрии, но перенесенной в другую предметную область.

Симметризация задачи настройки искусственных нейронов и учета корреляционных связей их выходных состояний

Следует отметить, что наиболее популярные статистические критерии [1, 2], к сожалению, имеют сильные корреляционные связи их решений.

В частности, сильные корреляционные связи имеют следующие статистические критерии:

• •    хи -квадрат критерием ( x2 ), IVP.^l’ n ^ 0.344;

• •    критерием Крамера-фон Мизеса (KfM), IVP.^P n ^ 0.404;

• •    критерием Фроцини (Fr), IVP^P n ^ 0.424;

• •    критерий Андерсона-Дарлинга (AD), IVP^P n ^ 0.396;

• •    логарифмический критерий Андерсона-Дарлинга (ADL),

P i ^ P 2 ^ P ee ^ 0.362.

При оценках работы статистических критериев в группе удобно выполнять симметризацию задачи.

Для этого следует выбирать порог квантования нейронов таким образом, чтобы вероятности ошибок первого и второго рода были близки (почти равновероятны).

Для хи -квадрат нейрона квантование выходных данных сумматора нейрона по порогу -64 дает следующее значение вероятностей ошибок:

P i « 0.343 « P 2 « 0.346 » P ee « д/p^P « 0.344.

Естественно, что каждый критерий (каждый нейрон) будет иметь свое значение порога сравнения и свое значение равновероятных ошибок – P EE . При симметризации данных необходимо вычислять среднее геометрическое всех равновероятных ошибок:

~

^PEE ⁼

= 55 p X )Pf)^FrWA^^

« 0.385.

Для учета влияние коэффициентов кор- реляции данных разных статистических териев необходимо заменить исходно не симметричную корреляционную матрицу на полностью симметричную:

■ 1	r 1	r 2	r 3	r 4		■ 1	r	r	r	r
r l	1	r 5	r 6	r 7		~	1	r	r	r
Г 2	r 5	1	r 8	r 9	^	~	r	1	r	~
r	r 6	r 8	1	r 10		r	r	r	1	r
_ r 4	r 7	r 9	r 10	1 _		. ~	r	r	r	1 _

9       0.5 п 2— n где      ~ « EIr}= 2     • E14    (1)

n - 2 n   i _{= 1}

Данные о коэффициентах корреляции, перечисленных выше классических статистических критериев и о среднем значении их модулей, приведены в табл. 1.

Таблица 1. Коэффициенты корреляции группы сильно зависимых статистических критериев для малой выборки в 16 опытов

	x 2	Fr	KfM	AD	ADL
x 2	1	0.445	0.486	0.392	0.662
Fr	0.445	1	0.943	0.613	0.76
KfM	0.486	0.943	1	0.666	0.831
AD	0.392	0.613	0.666	1	0.698
ADL	0.662	0.76	0.831	0.698	1
Усредненные по модулю значения коэффициентов корреляции ~ = 0.65
Среднее   геометрическое   вероятностей   ошибок PEE = 0.385 EE

Отметим, что сильные корреляционные связи нежелательны (см. табл. 2). В свя- зи с этим можно попытаться выделить группу нейронов (статистических критериев) со слабыми корреляционными связями:

• •    нейрон Гири (G), P i « P 2 « P ee ~ 0.231;

• •    нейрон хи- квадрат ( % ² ), IVP.^Ph ^ O.344;

• •    нейрон Девида-Хартли-Пирсона, (DXP), P i « P₂ « P ee » 0.295;

• •    нейрон Лоусена (L), P i » P₂ « P ee « 0.196;

• •    нейрон Колмогорова-Смирнова (КС), P i « P 2 « P ee * 0.41.

  Таблица 2. Коэффициенты корреляции группы слабо зависимых статистических критериев для малой выборки в 16 опытов

  кри-

  	x 2	G	DXP	L	KC
  x 2	1	-0.016	0.0017	-0.004	0.007
  G	-0.016	1	0.008	-0.024	0.008
  DXP	0.0017	0.008	1	0.002	0.015
  L	-0.004	-0.024	0.002	1	0.008
  KC	0.007	0.004	-0.008	0.008	1
  Усредненные по модулю значения коэффициентов корреляции ~ = 0.017
  Среднее  геометрическое  вероятностей  ошибок F~ff = 0.285 EE

  
  

Простота имитационного моделирования одинаково коррелированных данных

Из классической теории связи известно, что ошибки в кодах с высокой избыточностью могут быть скорректированы. При этом, чем длиннее код (чем больше его избыточность) тем больше ошибок можно обнаружить и поправить. Нейросетевая молекула рис. 2 способна иметь 256-кратную кодовую избыточность, однако, сколько ошибок в столь длинном коде может быть исправлено – неизвестно.

Все классические коды с обнаружением и исправлением ошибок строились на гипотезе независимости корректируемых разрядов. Мы не можем воспользоваться классикой избыточных кодов, обнаруживающих и исправляющих ошибки. Нам остается только один путь – имитационного моделирования длинных кодов с зависимыми разрядами.

Формально мы можем попытаться решать задачу имитационного моделирования данных с любой асимметричной корреляционной матрицей (1) [13]. Однако это имеет смысл только в том случае, если коэффициенты корреляции заранее вычислены на больших выборках. Если речь идет о вычислении коэффициентов корреляции на малых выборках, задача моделирования становится некорректной, так как вычисление по формуле Пирсона коэффициентов корреляции дает на малых выборках очень большую ошибку. Чем больше размерность задачи – n, тем больше будет ошибка моделирования асимметричных корреляционных матриц.

В этом контексте процедура симметризации задачи через усреднение модулей коэффициентов корреляции (1) является процедурой регуляризации вычислений. То есть, с ростом размерности задачи ошибка имитационного моделиров ания падает пропорционально л/ 0.5 ⋅ n ² - n .

При программной реализации симметричного имитационного моделирования корреляционных связей необходимо воспроизводить множество малых выборок. Функциональные связи имитатора выборок объемом 16 опытов на языке программирования MathCAD отображены на рис. 3.

x :=	z <- morm(16,0,1 + rnd(0.01)) for i e 0.. 256 x^ <- morm(16,0,1 + md(O.Ol)) aF 1.0 for i € 0.. 256 „ , [г+а (Я] X

Рис. 3. Программа, реализующая связывание 256 случайных параметров

a	f
9.37 2.98 2.0095 1.525 1.222 1.0 0.815 0.654 0.501 0.3333 0.127	0.01 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.30 0.90 0.99

Фрагмент программы связывания 256 векторов данных реализуется с использованием всего одного настраиваемого параметра – "а".

В итоге мы получаем данные с примерно одинаковой взаимной коррелированностью (рис. 4).

0 1 2 3 0 -0.851 -1.024 0.041 -0.749 1 0.269 -0.447 1.204 -1.662 2 -0.833 -1.14 -2.313 -1.96 3 -0.814 -0.708 -2.629 -0.824 4 -1.076 -0.208 0.716 1.621 5 1.01 -3.085 -2.23 -0.969 6 -1.388 -0.77 -1.054 -1.985 corr(?\^^ = 0338  corr(х®,^) = 0.532

corr(х®,х®) = 0.4-8 corrtx® , х®) = 0.481 corr(ММ) = 0.211 corr(x<®,x<12s>) = 0.527 corr(x®, M) = 0.170 con(x®. X®S>) = 0.338 corr(x®^,x®) = 0355 corr(M^) = 0.203

Рис. 4. Результаты связывания между собой 256 векторов по 16 случайных данных с нулевым математическим ожиданием и почти единичным стандартным отклонением

Из рис. 4 видно, что из-за малого объемы выборок (всего 16 отсчетов) корреляционные связи между 256 параметрами кажутся достаточно случайными. На самом деле коэффициенты корреляции одинаковы.

В этом можно убедиться, увеличив примерно в 100 раз объем выборок, на которых вычисляются коэффициенты корреляции по формуле Пирсона. Для этого потребуется внести изменение в программный модуль рис. 3.

Получение длинных кодовых последовательностей квантованием предварительно связанных данных

Исходя из того, что корреляционные связи для 256 нейронов нейросетевой молекулы уже сцеплены программным модулем рис. 3, для получения длинных бинарных последовательностей достаточно выполнить квантование континуальных данных.

Так как данные симметричны, программа квантования (рис. 5) сравнивает данные всех нейронов с одинаковым порогом – "b". Значение порога подбирается таким образом, чтобы среднее значение оцифрованных данных – mean(k) – совпадало со средним геометрическим значением вероятностей ошибок объединяемых нейронов – ^~ P при многократном запуске программ.

for ieO.,236

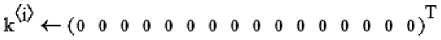
for ieo..256

for jeo.. 15

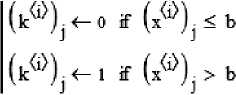
mean(k) = 0.333

Таблица связей

ь	ЕЕ
1.6405	0.05
1.27	0.10
1.035	0.15
0.831	0.20
0.6725	0.25
0.525	0.30
0.3825	0.35
0.252	0.45
0.0	0.50

Рис. 5. Программный модуль квантования данных симметричных нейронов

В итоге мы получаем длинные кодовые последовательности с коррелированными (сцепленными) между собой разрядами. При этом мы сталкиваемся с проблемой анализа длинных кодовых последовательностей. Если длина последовательностей 256 бит, то мы получаем 2 ²⁵⁶ состояний. Работать со столь длинными кодами сложно, в частности очень сложно вычислить энтропию таких кодов.

Упростить задачу удается, если перейти от самих кодов к расстоянию Хэмминга до интересующего нас идеального кода "0000….0000", соответствующего ситуации, когда все нейроны искусственной молекулы приняли одно и то же решение "0" – нормальная выборка.

Преимуществом перехода от обычных кодов в пространство расстояний Хэмминга является то, что исходное число анализируемых состояний 2 ²⁵⁶ экспоненциально снижается до величины (256+1) состояний.

Программный модуль перехода к расстояниям Хэмминга дан на рис. 6.

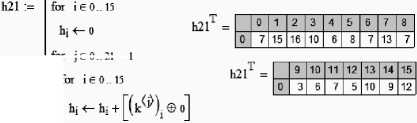
tor ie 0..21-1

h

Рис. 6 . Программный модуль вычисления 16 расстояний Хэмминга для 21 нейрона, каждый из которых обучен давать состояние " 0 " для малой выборки нормальных данных и состояние " 1 " для выборки равномерных данных

Использование простейшего кода коррекции ошибок 256-битного выходного кода нейросетевой искусственной молекулы

Следует отметить, что выходные коды нейросетевой молекулы имеют большинство состояний разрядов "0" и примерно 1/3 разрядов "1", если разряды слабо зависимы. Чем больше зависимость разрядов, тем хуже работают классические коды с обнаружением и исправлением ошибок.

В этом контексте искусственную молекулу целесообразно собирать из нейронов со слабо коррелированными откликами. Очевидно, что ориентироваться на худший вариант сильных корреляционных связей классических нейронов (табл. 1) нельзя. Нельзя также ожидать почти полного отсутствия корреляционных связей (табл. 2). Если исходить из гипотезы уровня корреляционных связей – 0.15 и среднего геометрического вероятностей ошибок – 0.33, то распределение расстояний Хэмминга оказывается близко к нормальному распределению (см. рис. 7).

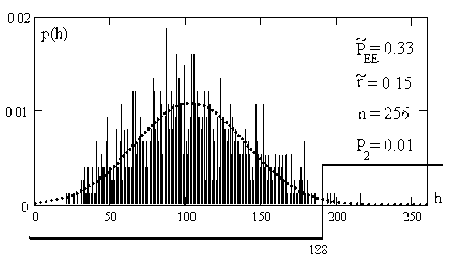
Рис. 7. Распределение расстояний Хэмминга выходных кодов искусственной статистической молекулы, собранной из 256 искусственных нейронов

Нормальность распределения данных позволяет легко вычислить порог кода корректировки данных для достижения ошибки второго рода P 2 =0.01, что вполне приемлемо для практики. Математическое ожидания расстояний Хэмминга составляет значение 103.3 бита, стандартное отклонение – 36.6 бита. При таком соотношении статистических моментов порог принятия решений составляет 188 бит с состоянием "0". При обнаружении числа "1" более 78 бит (менее 188 состояний "0") принимается решение об отвержении гипотезы о нормальности распределения значений малой выборки в 16 опытов.

Заключение

Таким образом, усложнение вычислений примерно в 256 раз при замене одного хи- квадрат критерия на 256 похожих слабо коррелированных преобразований должно позволить снизить вероятность ошибок с 0.344 до величины 0.01, в 34 раза меньше и вполне приемлемо для практики.

В прошлом веке было создано порядка 200 статистических критериев, при этом математики, их создававшие, стремились к повышению мощности каждого из критериев.

В XXI в. появилась возможность нейросетевого объединения множества критериев, однако при этом придется при создании новых статистических критериев учитывать их коррелированность с уже известными критериями.

Кроме того, ожидается появление еще одного дополнительного фактора конкуренции между коммерческими фирмами, такими как: MathCAD, STATISTICA, Maple, MatLAB. Скорее всего, именно фирмы коммерческой математики, конкурируя между собой, решат задачу нейросетевого обобщения множества статистических критериев.