Использование элементов контекстного обучения при подготовке будущих учителей математики

Модель учителя XXI века четко определяет личностные качества, универсальные, общепрофессиональные и профессиональные компетенции, закрепленные в образовательных программах бакалавриата, отражающие специфику работы на разных уровнях образования, а также методы оценки выполнения требований профессионального стандарта педагога [5]. Однако профессиональное развитие будущего учителя математики в вузе сопровождается рядом проблем, нерешенность которых негативно влияет на качество школьного математического образования и профессиональной подготовки педа-

Арзамасский филиал Национального исследовательского Нижегородского государственного университета имени Н.И. Лобачевского

гога. Укажем некоторые из таких проблем, возникающих при освоении дисциплин обязательной части образовательной программы направления подготовки «Педагогическое образование (с двумя профиля подготовки)»:

• •    невысокий начальный уровень подготовки обучающихся по математике, отсутствие мотивации и интереса к ее изучению и профессии в целом, о чем свидетельствуют данные Рособрнадзора: минимальный балл при сдаче еди-

  ного государственного экзамена (далее – ЕГЭ) за 2023 год составил 57–62;

• •    количество часов, отведенных на изучение рассматриваемых дисциплин для студентов бакалавриата, меньше по сравнению со специалитетом, что приводит к снижению уровня строгости изложения математических фактов, уменьшению возможностей развития абстрактного и логического мышления обучающихся средствами данных дисциплин;

НЕСТЕРОВА ЛАРИСА ЮРЬЕВНА

Российская Федерация, город Арзамас

LARISA Yu. NESTEROVA

Arzamas, Russian Federation

• •    малое количество обучающихся, способных качественно извлекать учебную информацию из текста школьных, вузовских учебников и соотносить ее с будущей педагогической деятельностью.

Наличие перечисленных проблем свидетельствует о том, что в современных условиях усиливается разрыв между уровнем подготовки выпускника школы к обучению в вузе и требованиями к обучению будущего педагога. В современных условиях при подготовке учителя математики приобретают актуальность технологии обучения, применяя которые, можно повысить качество образования и математической грамотности, сформировать профессиональную компетентность студента.

Основная часть. В основе предлагаемой нами системы работы по формированию компетенций буду- щего учителя математики лежит технология контекстного обучения. Ее основоположник, А.А. Вербицкий определил контекстное обучение как «обучение, в котором с помощью всей системы дидактических форм, методов и средств моделируется предметное и социальное содержание будущей профессиональной деятельности специалиста, а усвоение им абстрактных знаний как знаковых систем наложено на канву этой деятельности. Учение в условиях такого процесса приобретает несколько иные характеристики. Оно выступает формой личностной активности, которая обеспечивает воспитание необходимых предметно-профессиональных и социальных качеств личности специалиста» [1, с. 32].

Контекстное обучение – это целостная педагогическая система, направленная на развитие профес- сиональных возможностей обучающего, его готовности к самореализации и саморазвитию, на обретение ценностных смыслов труда благодаря последовательному воссозданию в учебном процессе тех контекстов, которые присущи осваиваемой профессии учителя.

У будущего педагога появляется возможность понять значение изучения тем, разделов дисциплин вузовской программы для профессиональной деятельности. Происходит осмысление студентами теоретических знаний, превращающихся из «культурных консервов», пригодных лишь для сдачи экзаменов, в живое знание, в ориентировочную основу предстоящей профессиональной деятельности, которая формируется «здесь и теперь» [2] в моделируемых ситуациях компетентного предметного действия и поступка.

ИСПОЛЬЗОВАНИЕ ЭЛЕМЕНТОВ КОНТЕКСТНОГО ОБУЧЕНИЯ ПРИ ПОДГОТОВКЕ БУДУЩИХ

УЧИТЕЛЕЙ МАТЕМАТИКИ

За период обучения в вузе обучающийся трансформирует содержание знания из прошлого через настоящее в будущее. При этом он осуществляет попытку создания своей методической «копилки» как в содержательном, так и в технологическом аспекте. Будущий учитель осознает свою значимость в осваиваемой профессии, что приводит к активизации образовательной деятельности.

В контекстном образовании А.А. Вербицкий выделил три базовые формы деятельности студентов:

• •    учебная деятельность академического типа (лекции, практические занятия и т.д.);

• •    квазипрофессиональная деятельность (игровые формы и др.);

• •    учебно-профессиональная деятельность (производственная практика, научно-исследовательская работа студентов, «реальное» дипломное проектирование).

Также выделяются другие формы обучения в вузе при переходе от одной базовой формы к другой.

Итак, технология описывает последовательный переход «от учения к труду» [2, с. 63]. Предполагается, что процесс обучения построен следующим образом: одна форма деятельности учения последовательно трансформируется в другую, все более приближается к формам организации профессиональной деятельности, но не утра- чивает при этом своих педагогических свойств и возможностей.

Идеи А.А. Вербицкого получили свое развитие в различных частных подходах контекстного обучения в применении к конкретным специальностям:

• •    для будущих учителей математики (В.А. Далингер, Т.Д. Дубовицкая, М.Г. Макарченко и др.);

• •    для будущих юристов (В.Б. Грид-чина, Т.Н. Тарасова и др.);

• •    для экономических специальностей (Н.А. Бурмистрова, А.Н. Кар-тежникова, Л.А. Сергеева и др.);

• •    для негуманитарных специальностей вуза (Э.С. Бадмаева, О.Г. Ларионова, О.М. Калукова, С.В. Плотникова, М.Н. Швецова, и др.).

Так, М.Г. Марченко указывает на погружение будущего учителя математики в разнообразные профессиональные смыслы и выделяет четыре контекста в профессиональной направленности учителя: учебно-математический (школьная и вузовская математика), методико-математический (психологические, педагогические и методические сведения), логико-математический (философия, математическая логика, их образы в школьном курсе математики) и историко-математический (методологическая, хронологическая, фактологическая, биографическая информации)» [3,с. 17]. Одним из средств реализации концепции контекстного обучения в вузе в ходе преподавания курса «Методика математики», по мнению ученого,является система контекстных заданий.

Таким образом,за счет четко выстроенной системы обучения у студента происходит плавный переход к реальной профессиональной деятельности: от учебной деятельности академического типа к ква-зипрофессиональной деятельности и к базовым формам деятельности более высокого ранга, ориентированной на компетентностный подход, максимально приближенной к профессиональной деятельности будущего учителя.

Элементы контекстного обучения были использованы нами при построении образовательной деятельности в рамках реализации образовательной программы студентов направления подготовки «Педагогическое образование (с двумя профилями подготовки)» направленности Математика» и физика с первого по пятый курс. Нами внесены дополнения в технологию знаково-контекстного обучения, представленные на Рисунке.

В середине схемы располагаются три базовые формы деятельности (обозначенные сплошной линией окружности), переход от одной формы к другой происходит в процессе обучения. Студент, осваивая учебные дисциплины, постепенно осмысливает учебно-математический контекст учебного

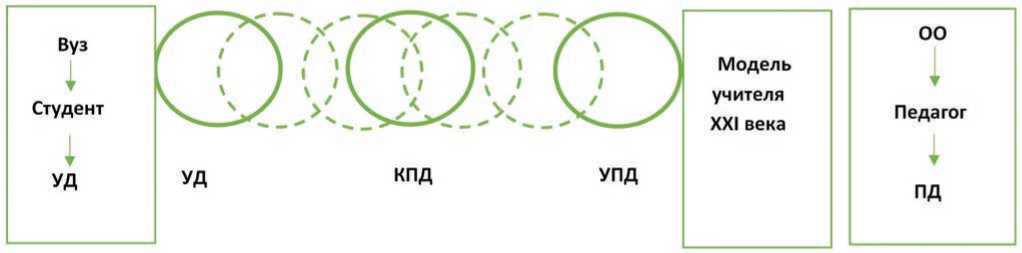
* УД – учебная деятельность; КПД – квазипрофессиональная деятельность; УПL – учебно-профессиональная деятельность; ОО – образовательная организация; ПД – профессиональная деятельность.

Рисунок. Технология знаково-контекстного обучения материала как школьной, так и вузовской математики.

Ценность данной технологии состоит в том, что у обучающегося на младших курсах осуществляется частичное осмысление методикоматематического контекста, накапливается опыт профессиональной деятельности, то есть происходит неполное формирование общепрофессиональных и профессиональных компетенций. Они получают дальнейшее развитие при изучении дисциплин на старших курсах, а также при написании курсовых работ, исследовательских проектов, выпускных квалификационных работ. На схеме такой переход обозначен окружностями, изображенными пунктирной линией.

Для обеспечения плавного перехода от одной формы деятельности к другой мы провели анализ содержания дисциплин, трудоемкости образовательной программы. Это позволило нам в учебном плане модуля «Предметно-методический» и части, формируемой участниками образовательных отношений, определить дисциплины, содержание которых прямо или косвенно участвует в наполнении профессиональной составляющей субъективного опыта будущего учителя математики предметными, методическими смыслами и научно-методическими контекстами. К таковым ним отнесли следующие дисциплины:

• •    «Алгебра», 16 зачетных единиц (далее – з.е.), 1, 2, 3 семестры (далее – сем.) изучения студентами;

• •    «Теория чисел», 2 з.е., 1 сем.;

• •    «Элементарная математика», 14 з.е., 1, 5, 6, 7, 9 сем.;

• •    «Теория вероятностей и математическая статистика», 3 з.е., 4 сем.

• •    «Методика обучения математике», 9 з.е., 5, 6, 7 сем.;

• •    «Числовые системы», 3 з.е., 9 сем.;

• •    «История математики», 2 з.е., 9 сем.

В каждой дисциплине мы выделили «сквозные» линии школьной и вузовской математики, ко- торые наиболее полно раскрывают целостность и трансдисциплинарные связи в направлении профессионализации знаний. Это позволяет провести обучение в целостном пространственно-временном контексте «прошлое – настоящее – будущее».

Обучение студентов с использованием элементов концепции контекстного обучения в первом семестре начинаем с дисциплины «Теория чисел», содержание которой напрямую связано с субъективным опытом первокурсника. В частности, изучаются темы «Деление нацело на множество целых чисел», «Деление с остатком», «Теорема Безу, схема Горнера» и др. Благодаря применяемой технологии, знания становятся для студента личностно значимыми.

Как показывает опыт работы, на практических занятиях будущий учитель может раскрыть свои уже имеющиеся профессиональная умения. Это умение объяснять материал и решать задачи; организовать беседу, слушать рассуждения обучающихся, задавать вопросы; вести общение; предлагать несколько способов решения одной задачи. Задача преподавателя – организовать деятельность первокурсника таким образом, чтобы попытаться создать целостный образ образовательного процесса по обучению математике, наполнить смыслами методические знания и действия.

Таким образом, первокурсник проецирует приобретенные зна-ния,умения и навыки на свою будущую педагогическую деятельность, осознавая, что только овладение предметными и методическими смыслами и научнометодическими контекстами позволит ему стать компетентным учителем математики.

Аналогичным образом мы строим обучение студентов младших курсов с использованием элементов контекстного обучения при освоении ими других дисциплин. Наиболее эффективны для их ре- ализации такие формы организации образовательной деятельности, как лекции-визуализации [4], проблемные лекции, работа в малых группах, лабораторные занятия. При этом самостоятельная работа обучающихся организуется с элементами не только учебной, но квазипрофессиональной деятельности. Выполненные студентами задания должны быть для них профессионально значимыми, они могут оценить овладение знаниями, методическими умениями «до» изучения и «после», непосредственно соотнести с будущей деятельностью педагога. Завершающим этапом является написание выпускной квалификационной работы, в которой будут собраны лучшие методические правила, теории, законы, принципы с учетом прохождения педагогических практик.

Заключение. Внедрение в процесс обучения будущего учителя математики элементов контекстного обучения увеличивает шансы подготовки компетентного и конкурентно способного педагога. Выделим этапы нашей работы.

• 1.    Определить совокупность дисциплин обязательной части образовательной программы направления подготовки «Педагогическое образование (с двумя профиля подготовки)». В качестве основных критериев отбора рассмотреть целостность отображения субъективного опыта обучающегося и преемственность его развития, трудоемкость образовательной программы.

• 2.    Выделить «сквозные» линии школьного и вузовского курсов математики в определенных дисциплинах для дальнейшего создания условий обучения студентов. При этом результаты учебной деятельности должны быть понятны, личностно и профессионально значимы. При дальнейшем освоении образовательной программы на старших курсах будущий учитель осмыслит методико-математический, историко-математический и логико-математический контек-

• ИСПОЛЬЗОВАНИЕ ЭЛЕМЕНТОВ КОНТЕКСТНОГО ОБУЧЕНИЯ ПРИ ПОДГОТОВКЕ БУДУЩИХ

• 3.    Использовать эффективные формы проведения занятий: лек-

• ции-визуализации, проблемные лекции, работа в малых группах, лабораторные занятия, самостоятельная работа – аудиторная и внеаудиторная.

УЧИТЕЛЕЙ МАТЕМАТИКИ сты учебного материала с точки зрения профессиональной направленности и субъективного опыта.

При реализации данных шагов использование элементов контекстного обучения способствует качественной подготовке будущих учителей математики.