Использование конформного преобразования в расчете температурного поля в пазу якоря двигателя постоянного тока

В приводе погружных устройств используются, как правило, электродвигатели постоянного тока, заполненные жидкими диэлектриками (ДПТД), относящиеся к классу высокоис-пользованных электрических машин [1] с повышенными электромагнитными нагрузками. В ряде случаев эти машины используются однократно, причем время работы их не превышает 10-20 мин. Жидкий диэлектрик необходим для компенсации внешнего давления. Для таких двигателей особенно актуальными являются вопросы нагрева активных элементов (обмоток, стали). Если при расчетах нагрева общепромышленных машин ограничиваются определением средней температуры их узлов и элементов, то в случае ДПТД из-за специфических условий их применения нужны данные по максимальным превышениям температуры активных частей (якоря и обмоток возбуждения). В данной работе предлагается способ расчета температурного поля в сечении якоря с использованием конформного преобразования [2].

Методика исследования

Выбирается сечение пазовой части в точке, где выполняется условие ^∂Т = 0, т.е. в наиболее нагретом сечении. Теплоперенос в осевом направлении в этом сечении отсутствует, и все тепло, выделяемое в сечении, отводится в радиальном направлении. На рисунке 1 изображено поперечное сечение открытого прямоугольного паза. Распределение температуры в активной части паза описывается уравнением Пуассона: 22

λ x ^d _dx ^T 2 + λ y ^d _dy ^T 2 +g(x, y) =0,                           (1)

где λ_x и λ_y - коэффициенты теплопроводности материала тела по осям х и y; g(x, y) - объемная плотность тепловыделения.

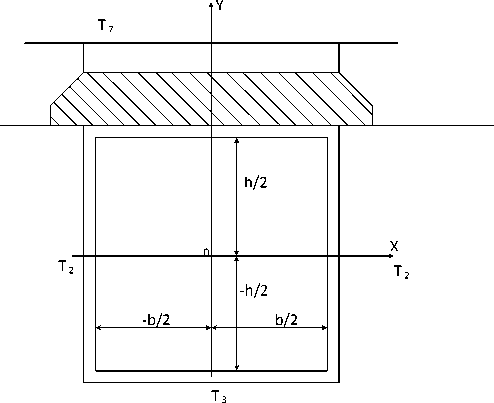
Рисунок 1 – К расчету температурного поля в поперечном сечении прямоугольного паза

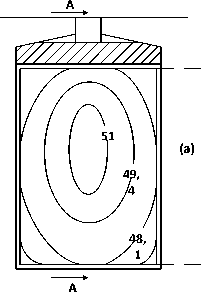
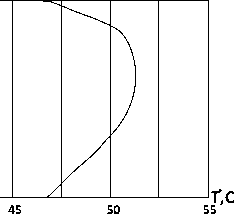
Для решения этого уравнения в пазу при неоднородных граничных условиях используется метод конечных интегральных преобразований Г.А. Гринберга [3], который нашел применение при расчете температурного поля в сечении обмотки возбуждения ДПТД [4]. Результаты расчета представлены на рисунке 2.

Kw\\\\\w\\

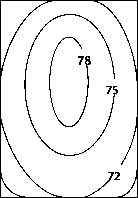
Рисунок 2 – Температурное поле в поперечном сечении паза якоря ДПТД-0,8 кВт (а) и 10,0 кВт (б)

Расчет температурного поля в овальном пазу (рис. 3 а) проводится следующим образом. Сечение активной зоны паза без существенных погрешностей заменяется криволинейной тра- пецией (рис. 3 б), уравнение нагрева которой имеет вид:

d ² T    1 dT     g 0 (1+β м ·T)

dr2    r dr        λл где λл – коэффициент теплопроводности; g0 - объемная плотность потерь; βм – температурный коэффициент сопротивления меди.

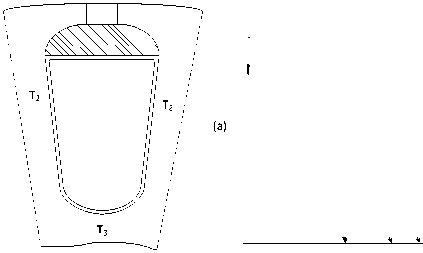
Рисунок 3 – К расчету температурного поля в поперечном сечении овального паза

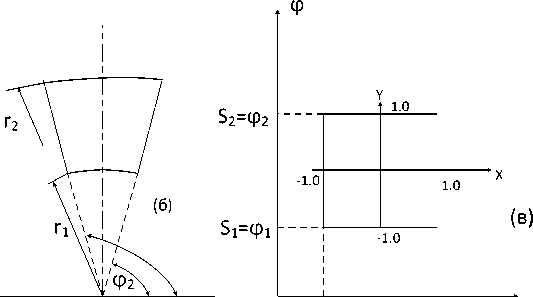
g g1= Lnr1     g2= Lnr2

Решить уравнение (2) из-за особенностей цилиндрической системы координат намного сложнее, чем уравнение (1). Поэтому для решения уравнения (2) в настоящей работе предлагается метод конформного преобразования [2], используемый для исследования плоских магнитостатических полей в областях с распределенными источниками. Как известно, данный метод ранее не применялся в расчетах нагрева электрических машин. Используем следующее преобразование координат (рис. 3 в):

g=Ln r, s=φ . (3)

Затем, чтобы привести интервалы изменения переменных g и s к интервалу – I, I , координаты линейно преобразуем в х и y:

x= ^2(g-g1) -1 , y= ^2(s-s1) -1 ,                      (4)

g 2 -g 1                s 2 -s 1

где g 1 = Ln r 1 , g 2 = Ln r 2 , s 1 = φ 1 , s 2 = φ 2 .

Распределение температуры в плоскости х,y подчиняется уже уравнению (1). Аналогично преобразуются граничные условия [5]. Для установления связи между плотностями потерь в сходственных точках U0 и υ0 рассмотрим элемент ∆SU = |∆r∆φ| в плоскости U. Отображение элемента в плоскости υ будет подобной фигурой, сторона которой связана со стороной исходного элемента соотношением

|∆r|=|Ln /r0|∆x .

Здесь Ln ^/x₀ - не производная, а обратная функция преобразования, т.е. Ln ^/x₀ = е^х0 . Через сечение ∆S_u и его отображение ∆S_υ протекает один и тот же тепловой поток dQ U = dQ υ ,                                             (6)

где dQ U = q(U O ) ∆S U , dQ υ = q(υ O ) ∆S υ .

Рассматривая (5) и (6), получим соотношение q(υ O )= q(U O ) ^∆Su = q(U O ) | Ln ^/x 0 |² .

∆Sυ

Коэффициент теплопроводности обмотки остается неизменным, так как при конформных преобразованиях физические свойства среды отображаемых областей не изменяются [6].

После перехода к прямоугольной системе координат задача решается методом Г.А. Гринберга. Затем полученное решение путем обратного преобразования переносится на исходную область. На рисунке 4 показаны полученные предложенным способом результаты расчета поля температур в овальном пазу якоря ДПТД-0,2 кВт.

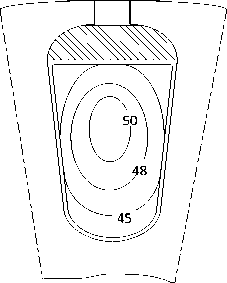
Рисунок 4 – Температурное поле в пазу якоря ДПТД-0,2 кВт

Выводы

Предлагается новый подход к расчету температурного поля в сечении овального паза двигателя постоянного тока с жидкостным заполнением, основанный на использовании конформного преобразования. Этот способ позволяет существенно упростить методику расчета плоского температурного поля с сохранением необходимой точности вычислений для такой сложной с точки зрении геометрии области, как овальный паз. Предлагаемую методику можно использовать и при нахождении распределения температуры в сечении пазов иной конфигурации, а также в обмотках возбуждения и обмотках дополнительных полюсов. Также эту методику можно рекомендовать для расчета нагрева электрических машин общего применения.