Использование математических редакторов в подготовке учителей математики

программные продукты используются нами при создании обучающих тренажеров и применяются на практике в подготовке будущих учителей математики в Набережночелнинском государственном педагогическом университете. Рассмотрим тезисно принципы применения данных моделей при решении задач и в конструктивных составляющих геометрических тренажеров.

Решение любой геометрической задачи на евклидовой плоскости начинается с построения чертежа, то есть с задачи конструктивной геометрии. В этой связи возможности предлагаемых систем будем рассматривать с точки зрения использования основных инструментов конструктивной геометрии и методов построения геометрической фигуры при помощи линейки и циркуля. При выполнении основных построений (2D-моделирования) возможности программы «Живая геометрия» оставляют желать лучшего. Например, затруднительно применение аксиомы циркуля для некоторых элементарных построений (например, для заданного отрезка, угла) [3]. Для выполнения этой работы приходится пользоваться основными командами из меню «Преобразование» или функциями копирования,что не соответствует указанной аксиоме циркуля.

К основным методам при решении задач на построение относят методы геометрического места точек, геометрических преобразований или алгебраический метод. При решении задач методом геометрического места точек чаще применяются основные команды из меню «Построение» и «Вид» и их в целом достаточно. Методы геометрических преобразований и алгебраический метод могут быть реализованы в рассматриваемой системе,при этом применяются в основном команды из меню «Преобразование» и «Измерения» [4]. Однако, визуализация этих методов в системе «Живая геометрия» несовершенна, потому что геометрические места точек плоскости, построенные командой «Живой след»,не определяются аналитически, то есть система не определяет уравнения построенных данной командой фигур. В программе «Живая геометрия» есть возможность создавать «инструменты». Под инструментом подразумевается алгоритм построения того или иного объекта по имеющимся данным. Инструменты целесообразно создавать лишь тогда,когда у пользователя отработано умение выполнять построение того или иного объекта. Создание инструментов, которые заменяют некоторый алгоритм построения, позволяет экономить время и применять принципы интерактивности в процессе преподавания геометрии [5].

Во многих учебных тренажерах по решению геометрических задач возникает необходимость проверки правильности построенного чертежа предложенной задачи средствами системы графического редактора. Здесь проверяются не шаги построения в компьютерной программе, а правильность выполнения условий предложенной задачи.

Приведем пример проверки выполненного пользователем чертежа к некоторой задаче путем осуществления измерений в редакторе Geometer’s Sketchpad.

Задача. Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно.

• 1.    Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.

• 2.    Найдите длину отрезка этой средней линии, заключенного внутри окружности.

На первом этапе решения задачи требуется проверить правильность выполненного чертежа. Требования тренажера: «Используя выполненный Вами чертеж, произведите следующие измерения, воспользовавшись командой «Длина» во вкладке «Измерения»: средней ли- нии MN параллельной основанию равнобедренного треугольника, высоты АН из вершины к основанию равнобедренного треугольника, радиуса r вписанной окружности».

У пользователя должен в итоге получиться чертеж к задаче (см. Рисунок 1).

Площадь треугольника S = p ∙ r , то есть

( V MH ² + AH ² + MN ) • r = 50,00 см 2 .

По другой формуле площадь треугольника S = AH ∙ MN , то есть

AH ∙ M ∙ N = 50,00 см² .

Тогда возможная схема проверки чертежа в тренажере представляется следующим образом: площадь треугольника вычисляется двумя способами и сравниваются полученные результаты. Таким образом, в тренажере осуществляется оценка разности:

I (V MH² + AH² + MN ) • r -– AH ∙ MN | = 0,00 см².

Если погрешность не превышает заданной величины, то тренажер (или преподаватель) засчитывает чертеж как правильно выполненную конструктивную задачу. Если погрешность не соответствует установленному уровню допустимой погрешности чертежа, то тренажер требует исправления. Например: «Ваш чертеж требует корректировки. Возможно, Вам необходимо исправить построения середин отрезков, биссектрис, перпендикуляров».

Таким образом, подтверждается возможность применения платформы The Gejmeter’s Sketchpad при изучении конструктивной геометрии и методов изображений в качестве простейшего и доступного инструментария построения учебных чертежей.

Рассмотрим некоторые возможности «Wingeom». Это геометрическая программа, которая предназначена для создания двумерных и трехмерных моделей. Она имеет схожие с «Geometer’s Sketchpad»

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ РЕДАКТОРОВ В ПОДГОТОВКЕ УЧИТЕЛЕЙ МАТЕМАТИКИ

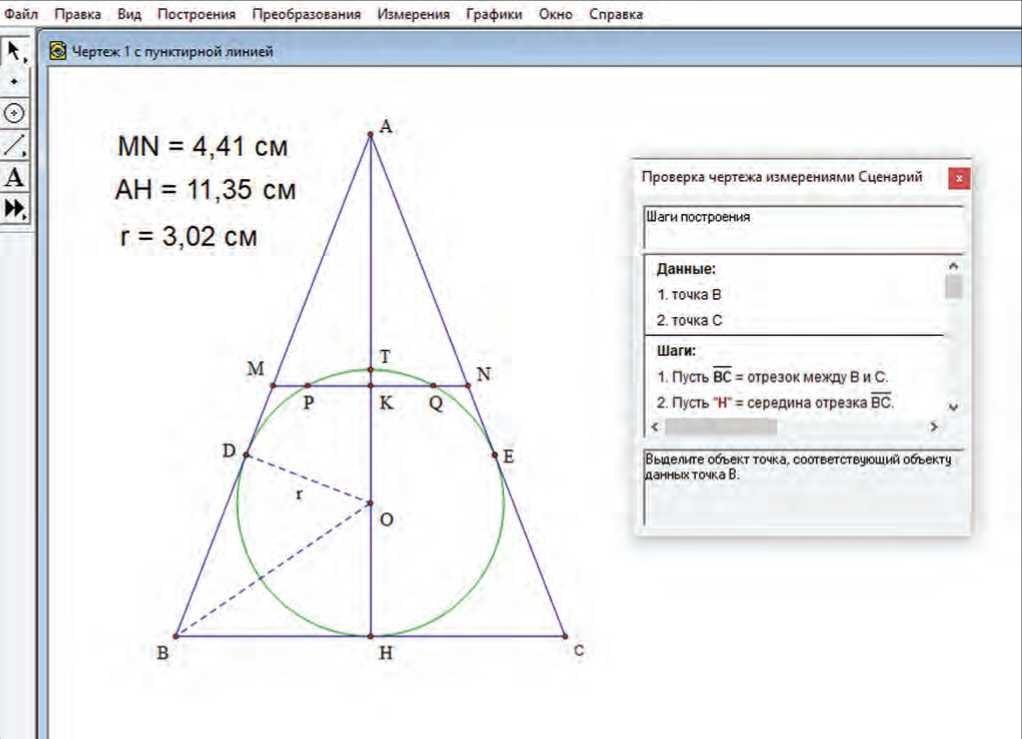
Рисунок 1. Проверка правильности построенного чертежа в редакторе Geometer’s Sketchpad

возможности в решении основных видов конструктивных задач. Однако есть и отличие – данная программа обеспечивает возможность строить точки по координатам, рассматривать изображения пространственных фигур в центральной проекции; вращение, смещение построенной фигуры. Преимущество платформы «Wingeom» перед «The Gejmeter’s Sketchpad» состоит в том, что она позволяет выполнять чертежи с вычислениями на модели Пуанкаре. Задачи можно решать или в круге, или на полуплоскости. Для демонстрации основных функций программы «Wingiom» рассмотрим работу в ее вкладке « 2-dim» на верхней полуплоскости.

Задача. Треугольник АВС задан углами: ∠ ABC = 30°, ∠ CAB = 80°, ∠ BCA = 45°. Требуется найти стороны и площадь треугольника.

Воспользуемся возможностями программы. Зададим треугольник по трем углам. Для этого необходимо применить команду «Hyperbolic», затем во вкладке «View» выбрать команду «Upper half-plane». Далее работаем на верхней полуплоскости, используя команды «Units», «Triangle» «0:ААА». Соответствующие вычисления производим с использованием команд вкладки «Meas». Программа также позволяет просмотреть историю произведенных действий пользователя. Чтобы просмотреть произведенные действия необходимо последовательно применить команды «Other», «Lists» «History». Появиться окно (см. Рисунок 2), в котором будет прописан каждый шаг работы.

Таким образом, можно создать тренажер по решению задач о треугольнике: нахождение всех его ше- сти элементов (трех сторон и трех углов) и площади по каким-либо трем данным элементам, определяющим треугольник, используя основные соотношения в нем.

Возможности рассматриваемой программы достаточны для изучения геометрии Лобачевского. Она позволяет рассматривать движения плоскости Лобачевского, моделировать образы фигур при этих движениях (см. Рисунок 3), решать конструктивные задачи, строить элементарные линии плоскости.

Система «Wingeom» работает с метрикой r . Элемент площади определяется формулой

, з dx X dy ds = r² 2 ,

y при r = 1. В этом случае площадь фигуры G на Λ2 вычисляется по формуле:

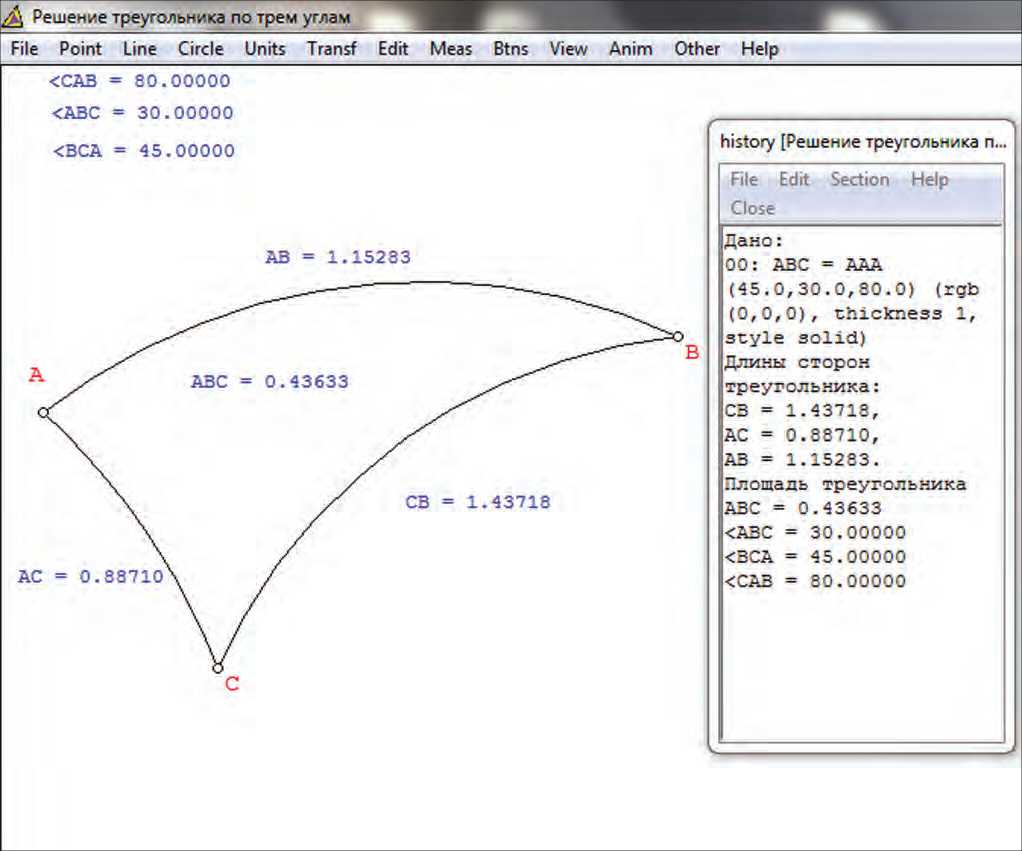
Рисунок 2. Сценарий решения задачи в «Wingeom»

s =

JJ

dx x dy

2 ^y

Однако, в этой системе не предусмотрена возможность вычисления интегралов. Для успешного решения задач на нахождение площадей при использовании тренажера рекомендуется первоначально рассмотреть площади элементарных фигур, например, треугольника. При этом требуется обосновать, что площадь треугольника определяется соответствующим дефектом σ = π – α – β – γ, где σABC = α + β + γ – сумма внутренних углов треугольника. Тогда нахождение площади можно осуществить двумя способами (опре- делением дефекта и двойного интеграла) и проверить полученные вычисления с применением системы «Wingeom». Таким образом, рассматриваемая система является эффективным инструментарием в качестве тренажера по решению задач плоскости Лобачевского.

Для конструирования некоторых тренажеров и формирования у обучающихся содержательных конструктивных навыков необходимы специализированные математические пакеты с более широким функционалом в области 3D-моделирования. В качестве подобного инструментария рассмотрим возможности системы моделирования Rhinoceros 3D в тандеме с Grasshopper. Grasshopper, будучи плагином для Rhinoceros 3D, дает возможность создавать визуальные программы, которые называются определениями. Они состоят из node,объединенных связями – это функциональные блоки («компоненты»), которые создаются на рабочем окне («холсте»). Популярность данной программы основана, прежде всего, на ее универсальности. Использование этого ПО позволяет целостно охватывать содержание основных разделов метода изображения и некоторых смежных дисциплин, в частности информатики. Возможности визуализации превращают математическую модель в форму, доступ-

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ РЕДАКТОРОВ В ПОДГОТОВКЕ УЧИТЕЛЕЙ МАТЕМАТИКИ

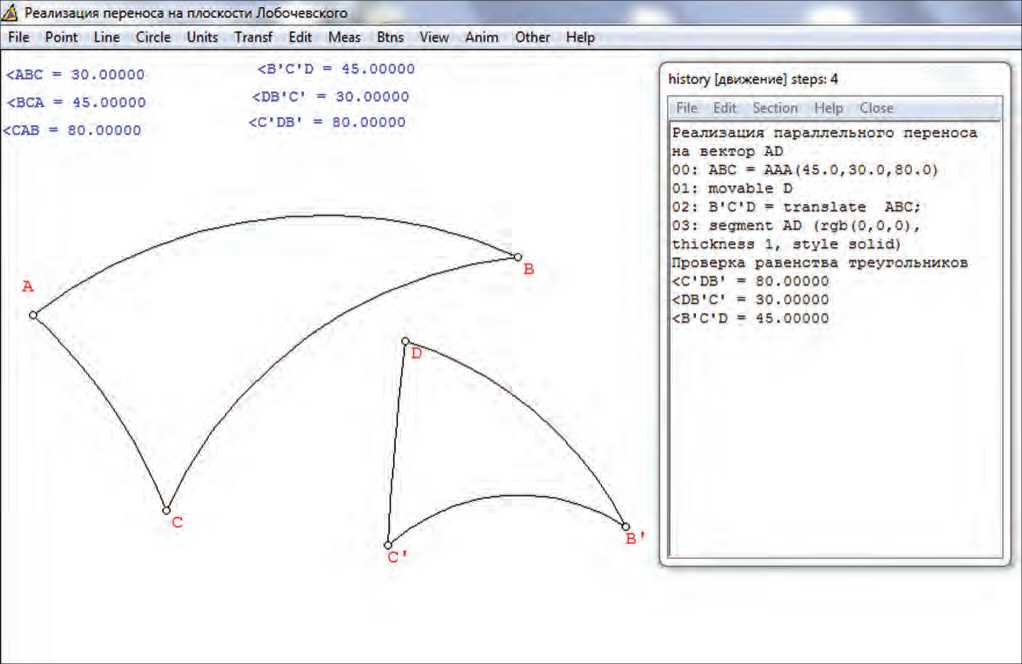
Рисунок 3. Моделирование образов фигур при движении на плоскости Лобачевского

ную для зрительного восприятия (render). На этапе прорисовки компьютерной графики и наложения текстуры (рендеринга) становятся видны все позиционные свойства геометрических фигур.

Рассмотрим воплощение учебной задачи в среде визуального программирования Grasshopper на примере описания теоремы де Гуа в трехмерном пространстве как аналога теоремы Пифагора в пространстве. Используя возможности измерения площадей, убеждаемся, что для всякого прямоугольного тетраэдра выполняется равенство, утверждаемое теоремой де Гуа (см. Рисунок 4):

S ABC S ABD + S BDC + S ADC "

Система Rhinoceros 3D позволяет легко трансформировать построенную фигуру в различные формы. Grasshopper и Rhinoceros 3D дают возможность установить точный параметрический контроль над моделями, что позволяет решать различные учебные конструктивные и исследовательские задачи. Возможности системы Grasshopper и Rhinoceros 3D выступают в роли компьютерной поддержки обучения. Рассмотрим исследование гипотезы: справедливо ли обратное утверждение теоремы де Гуа как аналога обратной теоремы Пифагора в пространстве? Возможности трансформации тетраэдра в рассматриваемой системе позволяют легко получить 3D модель, опровергающую справедливость обратного утверждения (см. Рисунок 5).

Данный пример показывает, что предлагаемая система является эффективным инструментом при разработке составляющих математических тренажеров по решению задач различных уровней и видов: учебно-математических, исследовательских. Система позволяет во многом автоматизировать процесс создания геометрического чертежа, компактно его хранить и мно- гократно использовать, а в случае необходимости вносить в имеющийся чертеж коррективы. Применение проектора и интерактивной доски в обучении геометрии позволяет максимально эффективно использовать время занятия. Интерактивная доска и возможность построения трехмерной модели позволяют выполнять дополнительные построения, а затем сохранять полученные чертежи для последующего использования. Эти же задачи могут быть предложены при изучении разделов 3D-моделирования. Мы убедились на практике, что рассматриваемая система полностью поддерживает теорию и практику методов изображения и решения стереометрических задач, позволяет оценивать действия будущего учителя математики в организации решения геометрической задачи с точки зрения дидактики, психологии, методики и аксиоматики геометрии.

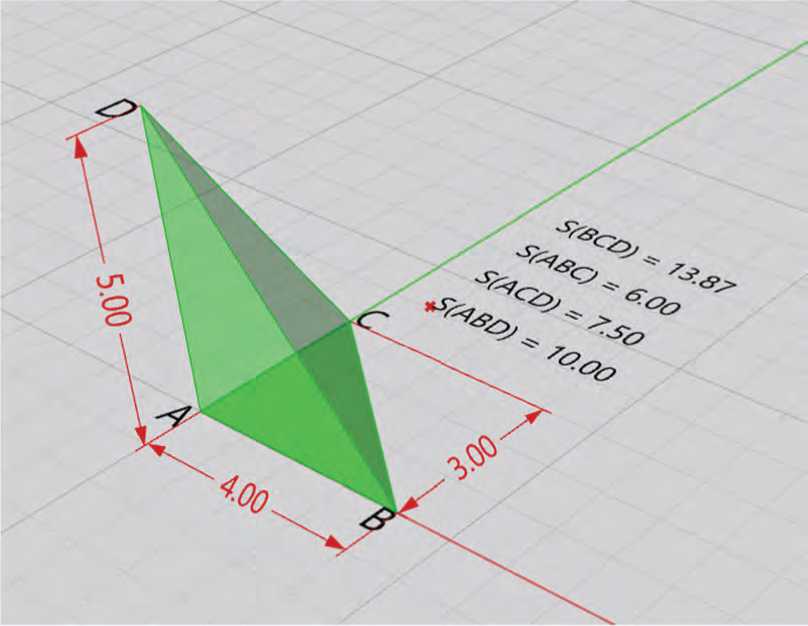
Рисунок 4. Визуализация равенства теоремы де Гуа для прямоугольного тетраэдра в Grasshopper

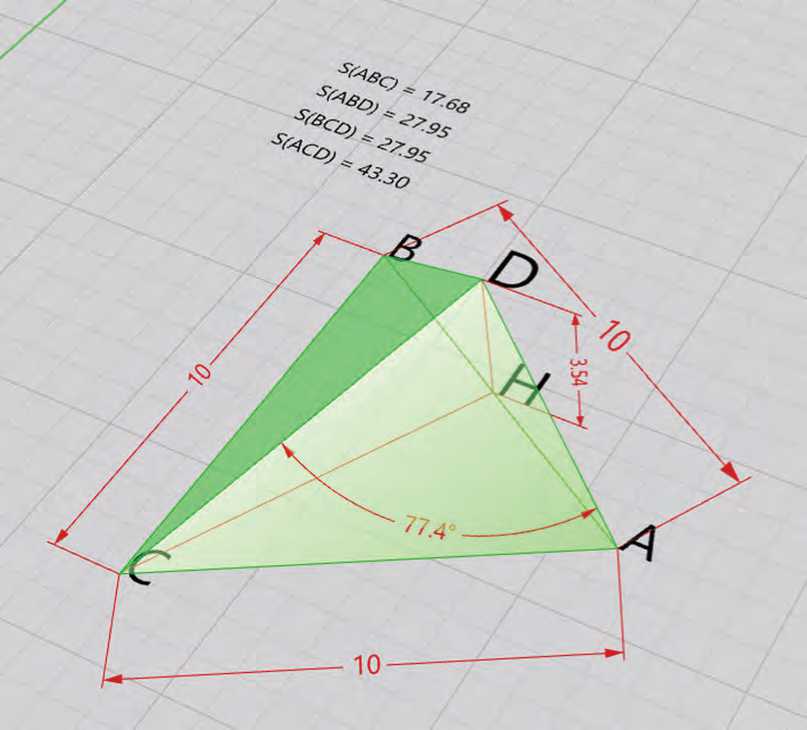
Рисунок 5. Проверка равенства теоремы де Гуа для непрямоугольного тетраэдра средствами Grasshopper

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ РЕДАКТОРОВ В ПОДГОТОВКЕ УЧИТЕЛЕЙ МАТЕМАТИКИ

Все приведенные выше платформы успешно используются нами при создании обучающих тренажеров и применяются на практике в подготовке будущих учителей математики в Набережночелнинском государственном педагогическом университете. Визуализации объектов стереометрических задач из курса геометрии могут быть также рассмотрены на занятиях как задачи раздела 3D-моделирования, что позволит формировать у будущих педагогов широкий ряд компетенций.

Предложенная конструктивная модель обучения решению позиционных задач с применением средств 3D-моделирования может рассматриваться как эффективный инструментарий, основанный на использовании информационных технологий в сфере образования. На наш взгляд, применение подобных программных продуктов принесет пользу не только студентам педагогических вузов, но и преподавателям математики. В настоящее время обучающимися по программам бакалавриата и ма-

гистратуры рассмотренные методы используются во время учебной практики в средних общеобразовательных школах города.

Подведя итог, отметим, что подобное применение данных программных продуктов на занятиях и в тренажерах выступило как дополнительный ресурс предметно-методического модуля ядра дисциплины «Геометрия» высшего педагогического образования по направлению подготовки «Педагогическое образование».