Использование технологии развития критического мышления (ТРКМ) при изучении темы «производная» в вузе

В эпоху информационного бума, когда информация льется на нас со всех сторон, ключевым становится умение анализировать ее, отсеивать ложь и применять знания на практике. Современное образование должно готовить специалистов, способных ориентироваться в этом потоке и успешно работать в условиях новой информационной реальности. Для этого необходимо развивать различные аспекты мышления, и особенно критическое.

Критическое мышление – это неотъемлемый навык современного профессионала. Д. Халперн (2000) дает следующее определение критического мышления: «Использование таких когнитивных навыков и стратегий, которые увеличивают вероятность получения желаемого результата. Отличается взвешенностью, логичностью и целенаправленностью. Другое определение ‒ направленное мышление» (Халперн, 2000: 53).

«Человеку, пользующемуся критическим мышлением, свойственны следующие качества:

• 1.    Готовность к планированию. […] Планирование ‒ первый и очень важный невидимый шаг к критическому мышлению. Постоянно упражняясь, каждый может развить в себе привычку планировать.

• 2.    Гибкость. […] Человек с ограниченным умом негативно относится к любым новым идеям, заявляя: “Я и без этого всегда обходился”. […] Критически мыслящий человек готов мыслить по-новому, пересматривать очевидное и не отступаться от задачи, пока она не будет решена.

• 3.    Настойчивость. […] Мышление ‒ это напряженный труд, который требует от человека терпения и настойчивости. Он может утомить вас не меньше, чем труд физический, но способен принести даже большее удовлетворение.

• 4.    Готовность исправлять свои ошибки. Все мы время от времени ошибаемся. Думающие люди, вместо того чтобы попытаться оправдать свои ошибки, умеют их признавать и тем самым учатся на них. Прислушиваясь к мнению окружающих, они стремятся понять, в чем неправы, и найти причины ошибки. Такие люди могут признать свои стратегии действия неэффективными и отвергнуть их, выбирая новые и совершенствуя свое мышление.

• 5.    Осознание. […] Оно подразумевает наблюдение за собственными действиями при продвижении к цели. Критически мыслящие люди развивают привычку к самоосознанию собственного мыслительного процесса.

• 6.    Поиск компромиссных решений. Групповые формы деятельности являются преобладающими в современном мире. Критически мыслящему человеку необходимо обладать как хорошо развитыми коммуникативными навыками, так и умением находить решения, которые могли бы удовлетворить большинство. Без этого даже самые светлые головы не смогут воплотить свои мысли в конкретные дела» (Халперн, 2000: 45).

С.И. Заир-Бек и И.В. Муштавинская в своей работе1 отмечают, что по Дж. Бареллу можно выделить характерные особенности личности, обладающей развитым критическим мышлением. К ним относятся: умение находить выход из сложных ситуаций, настойчивость в преодолении трудностей, саморегуляция, восприимчивость к инновациям и совместной работе, внимательное отношение к чужому мнению, сочувствие, принятие неоднозначности; способность анализировать вопросы с различных сторон, выявлять взаимосвязи; уважение к чужой точке зрения, рассмотрение альтернативных вариантов; умение формулировать вопросы, выстраивать логические цепочки; анализировать эмоциональное состояние и мысли, прогнозировать события, аргументировать предположения и определять задачи, применять знания в новых контекстах, любознательность и активное восприятие информации.

В русле гуманистической парадигмы для развития критического мышления необходимы личная мотивация к учебе, проявление инициативы и осознанный подход к процессу обучения.

Авторы технологии РКМЧП (развитие критического мышления через чтение и письмо) Ч. Темпл, К. Мередит и Д. Стил считают, что критическое мышление – это проявление любознательности и использование исследовательских методов для поиска ответов на вопросы. «Критическое мышление работает на многих уровнях, не довольствуясь фактами, а вскрывая причины и следствия этих фактов. Критическое мышление предполагает вежливый скептицизм, сомнение в общепринятых истинах, выработку точки зрения по определенному вопросу, способность отстоять ее логическими доводами. Критическое мышление – это не отдельный навык, а сочетание многих умений»2.

Для успешного формирования навыков критического мышления у студентов исследователи подчеркивают ряд важных факторов: наличие времени и условий для практического применения знаний, возможность для рефлексии, толерантность к разнообразию точек зрения, вовлеченность в учебную деятельность, создание безопасной среды без страха критики, убежденность в потенциале каждого студента к аналитическому мышлению и признание значимости критического подхода.

Необходимо, чтобы студенты чувствовали уверенность в значимости своих взглядов, принимали деятельное участие в образовательном процессе, проявляли уважение к мнению других, а также были способны как к выражению собственных оценок, так и к их временному воздержанию.

Жан Пиаже (2008), швейцарский психолог, отмечал, что к 16‒17 годам создаются наиболее благоприятные условия для развития критического мышления, что соответствует возрасту студентов первого курса.

Технология развития критического мышления (ТРКМ) использует чтение и письмо как ключевые инструменты. Чтение способствует анализу и оценке информации, а письмо – выражению мыслей. ТРКМ включает три этапа: вызов, осмысление содержания и рефлексию.

На этапе вызова преподаватель активизирует знания студентов и помогает формулировать вопросы по теме. Это позволяет выявить противоречия и непонятные моменты, определяющие направления изучения. Каждый студент сам решает, что ему необходимо изучить. Работа ведется индивидуально и в группах, что формирует коммуникативные навыки, так как высказывать свое мнение среди одногруппников более комфортно, чем перед большой аудиторией. Информация, собранная на этом этапе, обсуждается и фиксируется в письменном виде.

На этапе осмысления происходит анализ материала в парах или группах с использованием новой информации (текст, изображение, лекция и т. д.). Студенты сопоставляют новый материал со своими знаниями и опытом, выявляют непонятные моменты и проводят анализ. Для этого этапа требуется достаточно времени и применение различных приемов.

На этапе рефлексии студенты осмысливают полученные знания и формулируют выводы, что помогает увидеть достигнутые результаты. Знания становятся собственными, происходит структурирование мыслей и выстраивание новых представлений. Понимание становится долгосрочным, если студент грамотно излагает информацию своими словами. Рефлексия проводится в письменной и устной форме и включает творчество, анализ и интерпретацию изученного материала.

Эти этапы помогают студентам активно включаться в образовательный процесс, решать задачи и глубже понимать изучаемый материал.

Многие преподаватели считают, что использование ТРКМ затруднительно на занятиях по математике из-за сложности текстов и обилия терминов. Кроме того, возникает проблема выбора эффективных приемов, а также нехватка времени и методической литературы. Однако использование ТРКМ помогает преподавателю высшей математики решать образовательные и воспитательные задачи, создавать атмосферу творчества и сотрудничества, развивать математическую речь и коммуникативные навыки студентов. Результаты достигаются только на практике.

Приведем примеры приемов ТРКМ для изучения темы «Производная»1. На стадии «Вызов» можно использовать приемы «Ассоциативный ряд» и «Инсерт». В первом случае студенты перечисляют ассоциации, связанные с понятиями темы (скорость, дифференциальное исчисление, приращение, окрестность точки, предел, тангенс). Прием «Инсерт» предполагает пометки при работе с текстом лекции по определенным критериям:

• •    «V» – я это знаю;

• •    «+» – это новая информация для меня;

• •    «‒» – я думал по-другому, это противоречит тому, что я знал;

• •    «?» – это мне непонятно, нужны объяснения, уточнения.

В таблице 1 приведен пример приема «Инсерт» по теме «Производные элементарных функций».

Таблица 1 ‒ Прием «Инсерт»

Table 1 ‒ Insert Reception

V	+	-	?
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрическую функции	Формулы производных элементарных функций	Чтобы найти силу тока I ( t ), нужно уметь находить производную от U ( t )	В каких задачах практического характера применяются правила дифференцирования и формулы производных?

1 Дифференциальное и интегральное исчисление функции одной переменной (примеры и задачи) : учебное пособие / Е.Г. Рудаковская [и др.] / под ред. Е.Г. Рудаковской. М., 2013. 132 с.

Данный метод способствует развитию навыков работы с текстом, включая анализ и систематизацию информации. Если непосредственная обработка лекционного материала на занятии затруднена, студенты могут выполнить эту задачу самостоятельно дома, а затем обсудить результаты на занятии. Примерная технологическая карта занятия, а также другие примеры по данной теме представлены в работе С.А. Владыкиной (2023).

На этапе «Вызов» можно применить метод «Ключевые понятия», заключающийся в расстановке предложенных слов в определенном порядке для создания рассказа. Например, для темы «Производная» можно использовать набор слов: скорость, дифференцируемость, касательная, производная, ускорение, непрерывность, предел.

В начале занятия студентам предлагается определить истинность или ложность предложенных утверждений. После ознакомления с информацией (лекцией, учебным материалом) происходит возврат к утверждениям, оценка их достоверности на основе полученных знаний. Например, для темы «Производная» можно использовать таблицу с утверждениями (таблица 2).

Таблица 2 ‒ Прием «Согласны ли Вы с утверждением?» для темы «Производная»

Table 2 ‒ The “Do You Agree with the Statement?” Technique for the “Derivative” Topic

№	Согласны ли Вы с утверждением?	Ответ
1	Функция называется непрерывной, если f(х) → f(х 0 ) при х → х 0 , т. е. малым изменениям аргумента в точке х 0 соответствуют малые изменения значений функции	+
2	Механический смысл производной: производная пути по времени t равна ускорению в момент времени t 0	‒
3	Производной функции f в точке х 0 называется число, к которому стремится разностное отношение f ' (x) = ^	+
4	Если производная функции в критической точке меняет знак с отрицательного на положительный, то это точка локального максимума	‒
5	Если производная функции в критической точке не меняет знак, то в этой точке нет экстремума	+
6	Функция называется возрастающей на промежутке, если большему значению аргумента соответствует большее значение функции	+
7	Функция всегда принимает наибольшее значение в точке экстремума	‒

По теме «Геометрический смысл производной» таблица «Согласны ли Вы с утверждением?» может иметь следующий вид (таблица 3).

Таблица 3 ‒ Прием «Согласны ли Вы с утверждением?» для темы

«Геометрический смысл производной»

Table 3 ‒ The “Do You Agree with the Statement?” Technique for the Topic

“Geometric Meaning of the Derivative”

№	Согласны ли Вы с утверждением?	Ответ
1	Угол наклона касательной острый, если k= tg α < 0	‒
2	Угловой коэффициент касательной к графику функции равен k = У 2 -У 1 Х 2 -Х 1	+
3	Касательная параллельна оси ОХ при k= f ′(х 0 ) = 0	+
4	Уравнение касательной имеет вид у = --^(х - х0)	‒
5	Нормаль ‒ прямая, перпендикулярная касательной и проведенная в точке касания	+
6	Для определения угла наклона секущей к положительной полуоси ОХ применяется формула Лагранжа: / ' (с) = tg а = ^(у;-^- , где а - угловой коэффициент секущей	+
7	Точка перегиба определяется с помощью первой производной	‒

Еще один прием для этапа «Вызов» – «Круги по воде», универсальный инструмент для активизации знаний и речевой активности учащихся. Ключевое понятие записывается вертикально, и на каждую букву подбираются существительные, глаголы, прилагательные или устойчивые словосочетания, связанные с темой. Студенты проводят небольшое исследование, которое начинается в аудитории и завершается дома. Это расширяет их понимание изучаемого понятия.

На этапе «Осмысление» рекомендуется использовать прием «Кластер» («Интеллектуальная карта»), развивающий умение выделять главное и мыслить самостоятельно. Кластер (интеллект-карта) представляет собой структуру, где в центре находится основное понятие, а по краям – связанные с ним смысловые единицы. Рекомендации по составлению кластера «Грозди»:

• 1.    Оцените текст лекции: возможно ли разделение на смысловые блоки, выделение крупных и мелких смысловых единиц?

• 2.    Окажите помощь студентам в выделении смысловых единиц в виде вопросов, ключевых слов или фраз.

• 3.    Предложите студентам представить и обсудить свои интеллект-карты.

• 4.    Попросите установить связи между элементами интеллект-карты и объяснить их.

• 5.    Предложите выделить наиболее важные элементы.

На рисунке 1 приведен пример кластера в виде «грозди».

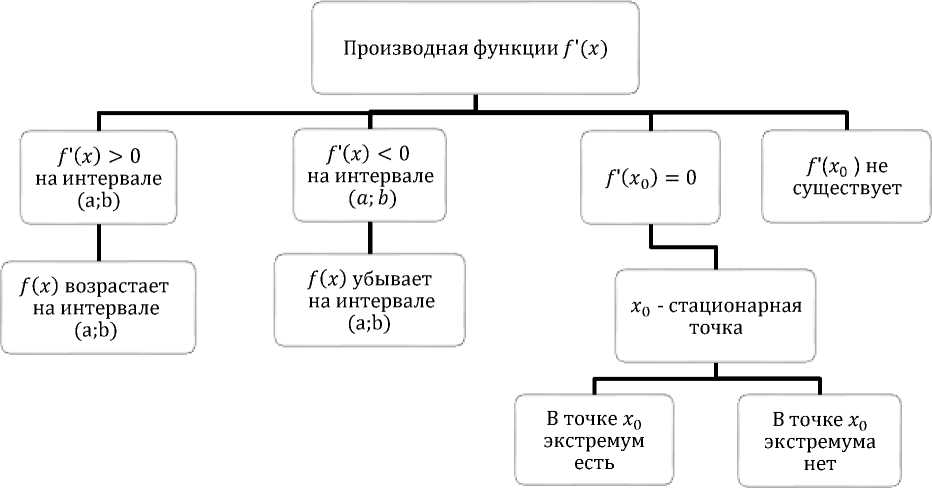
Рисунок 1 ‒ Кластер «Производная функции»

Figure 1 ‒ The “Derivative of a Function” Cluster

На рисунке 2 приведен пример кластера по теме «Применение производной».

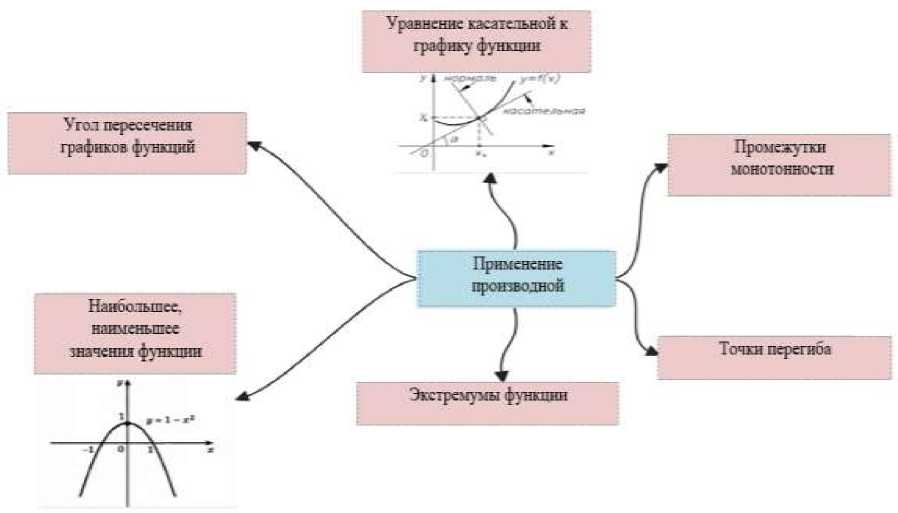
Рисунок 2 ‒ Кластер «Применение производной»

Figure 2 ‒ The “Derivative Application” Cluster

Метод «Денотатный граф» позволяет систематизировать материал, отличаясь от кластера тем, что в первой строке указывается главное понятие, во второй – действия, а в третьей – существительные. На рисунке 3 представлен пример денотатного графа по теме «Возрастание и убывание функции». Составление графа способствует осмыслению информации и установлению связей между понятиями.

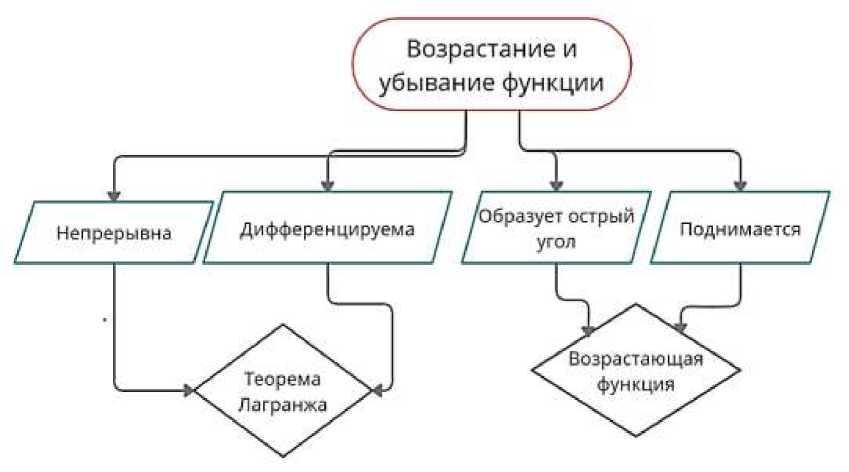
Рисунок 3 ‒ Денотатный граф «Возрастание и убывание функции»

Figure 3 ‒ Denotation Graph “Increasing and Decreasing Functions”

На этапе «Осмысление» в парах можно использовать взаимоопрос, когда студенты читают текст, останавливаются после каждого абзаца и задают друг другу вопросы разного уровня сложности по содержанию. Это способствует развитию коммуникативных навыков.

На этапе «Рефлексия» также применяются методы визуализации информации, например, создание интеллект-карт, где от центральной идеи расходятся связанные понятия. На рисунке 4 представлен пример интеллект-карт по теме «Экстремумы функции». Карту можно создать ин-

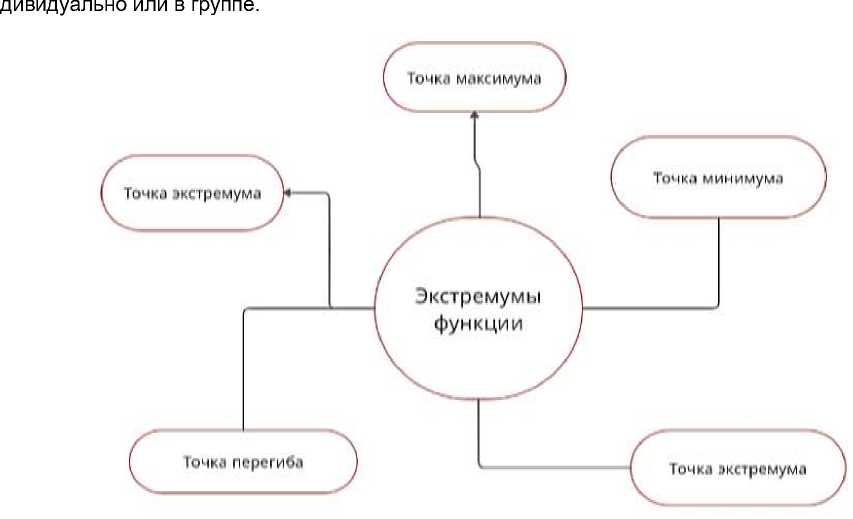
Рисунок 4 ‒ Интеллект-карта «Экстремумы функции»

Figure 4 ‒ Intelligence Map “Function extremes”

Еще один прием для этапа рефлексии – составление синквейна, стихотворения из пяти строк по правилам:

• •    первая строка – тема (существительное);

• •    вторая строка – описание темы (два прилагательных);

• •    третья строка – действия, относящиеся к теме (три глагола или деепричастия);

• •    четвертая строка – отношение к теме (фраза, пословица, цитата, афоризм);

• •    пятая строка – итог (одно слово, резюмирующее стихотворение).

Приведем пример синквейна по теме «Геометрический смысл производной»:

Смысл.

Дифференцируемый, угловой.

Возрастает, убывает, существует.

Угловой коэффициент касательной к графику.

Производная.

Основная задача этапа «Рефлексия» – формирование метапредметных умений, таких как выделение и краткое представление общих и особенных черт при сравнении понятий и явлений. Для развития аналитических способностей можно использовать прием «Сходства и различия» (индивидуально, в парах или группах) с использованием кругов Эйлера-Венна для представления общих и уникальных черт двух явлений (рисунок 5).

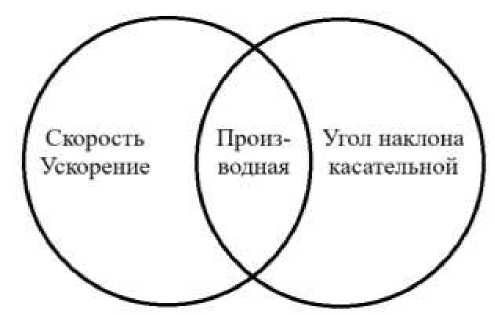
Рисунок 5 ‒ Общее ‒ уникальное

• Figure 5 ‒ General ‒ Unique

Таким образом, использование технологии развития критического мышления при изучении темы «Производная» на занятиях по высшей математике делает процесс обучения интересным и увлекательным, способствует глубокому включению студентов в обучение и повышает его эффективность. Студенты учатся принимать осмысленные решения, аргументировать свой выбор, проявлять инициативу и работать в команде. Они более ответственно относятся к своему образованию.

Разнообразие приемов ТРКМ позволяет использовать технологию на всех этапах занятия, помогая обучающимся лучше усвоить тему и развивать их мышление.

Внедрение ТРКМ позволяет преподавателю гибко адаптировать учебный процесс, учитывая индивидуальные особенности и потребности студентов. Активные методы обучения стимулируют познавательный интерес и формируют устойчивую мотивацию к изучению математики. Студенты не просто пассивно воспринимают информацию, а становятся активными участниками образовательного процесса, самостоятельно добывая знания и развивая навыки критического анализа.

Применение ТРКМ не ограничивается только темой «Производная». Данная технология может быть успешно интегрирована в преподавание других разделов высшей математики, а также в дисциплины естественно-научного и гуманитарного циклов. Важно помнить, что эффективность ТРКМ зависит от тщательной подготовки преподавателя, разработки методических материалов и создания благоприятной образовательной среды.

Использование технологии развития критического мышления предполагает создание на занятиях атмосферы сотрудничества и взаимоуважения. Студенты должны чувствовать себя комфортно, высказывая свои мысли и идеи, даже если они отличаются от общепринятых. Преподаватель выступает в роли модератора, направляя дискуссию и помогая студентам находить ответы на поставленные вопросы.

Таким образом, технология развития критического мышления является эффективным инструментом повышения качества математического образования. Она позволяет не только улучшить усвоение учебного материала, но и сформировать у студентов навыки, необходимые для успешной адаптации в современном мире. Внедрение ТРКМ в учебный процесс требует от преподавателя постоянного совершенствования своих методических навыков и готовности к инновациям.